एक सरल तंत्रिका नेटवर्क बनाएँ

एक सरल तंत्रिका नेटवर्क बनाने का अनुवाद

हम क्या करेंगे? हम एक सरल और बहुत छोटा तंत्रिका नेटवर्क बनाने की कोशिश करेंगे, जिसे हम आपको कुछ अलग करने के लिए समझाएंगे और सिखाएंगे । उसी समय, हम इतिहास और गणितीय जंगल में नहीं जाएंगे (ऐसी जानकारी खोजना बहुत आसान है) - इसके बजाय, हम आपको और खुद को चित्र और कोड के साथ समस्या को समझाने की कोशिश करेंगे (यह संभव नहीं है कि यह संभव होगा)।

तंत्रिका नेटवर्क में कई शब्द जीव विज्ञान से संबंधित हैं, तो आइए शुरुआत से शुरू करें:


मस्तिष्क एक जटिल चीज है, लेकिन इसे कई मुख्य भागों और कार्यों में भी विभाजित किया जा सकता है:



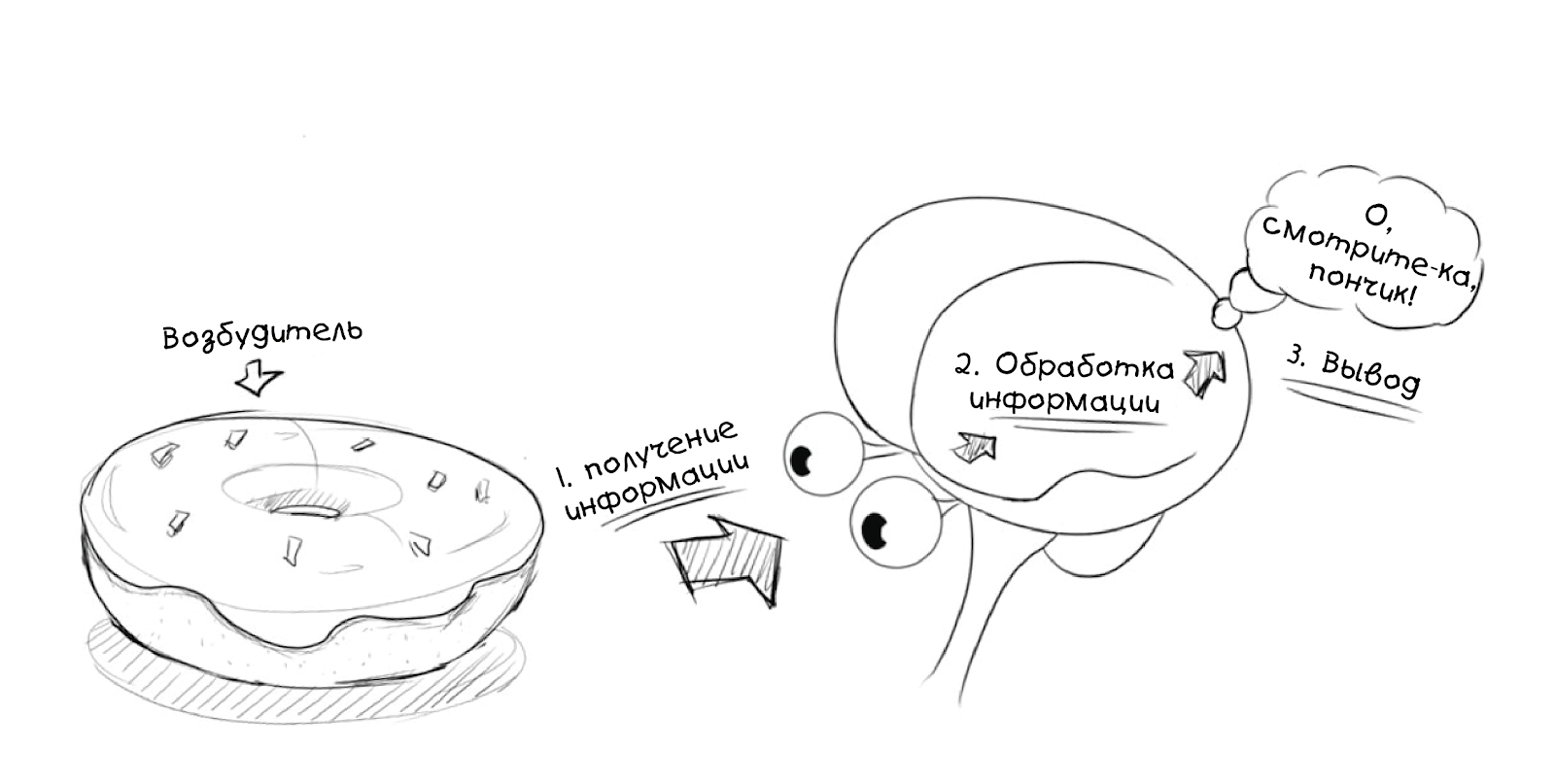
प्रेरक एजेंट आंतरिक भी हो सकता है (उदाहरण के लिए, एक छवि या एक विचार):



अब आइए मस्तिष्क के मूल और सरलीकृत भागों पर एक नज़र डालें:


मस्तिष्क आमतौर पर एक केबल नेटवर्क की तरह दिखता है।

एक न्यूरॉन मस्तिष्क में पथरी की मुख्य इकाई है, यह अन्य न्यूरॉन्स के रासायनिक संकेतों को प्राप्त करता है और संसाधित करता है, और, कई कारकों के आधार पर, या तो कुछ भी नहीं करता है, या एक विद्युत आवेग, या एक्शन पोटेंशियल उत्पन्न करता है, जो तब synapses के माध्यम से पड़ोसी से जुड़े न्यूरॉन्स को संकेत भेजता है:



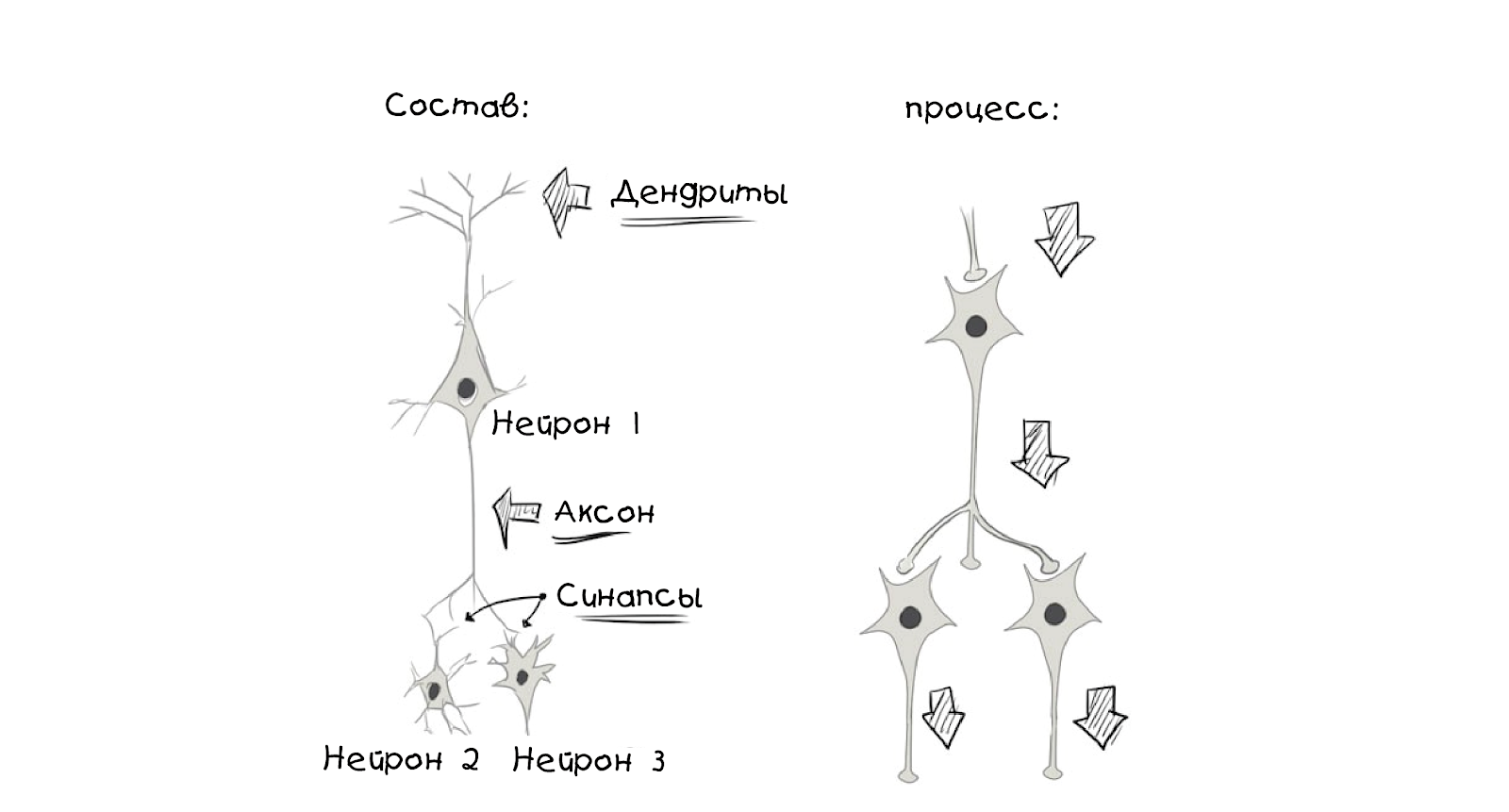
सपने, यादें, स्व-विनियमन आंदोलनों, सजगता, और वास्तव में जो कुछ भी आप सोचते हैं या करते हैं वह सब इस प्रक्रिया के कारण है: लाखों या अरबों न्यूरॉन्स विभिन्न स्तरों पर काम करते हैं और कनेक्शन बनाते हैं जो अलग-अलग समानांतर उप-प्रणाली बनाते हैं और एक जैविक तंत्रिका नेटवर्क का प्रतिनिधित्व करते हैं ।

बेशक, ये सभी सरलीकरण और सामान्यीकरण हैं, लेकिन उनके लिए धन्यवाद हम एक सरल वर्णन कर सकते हैं
तंत्रिका नेटवर्क:



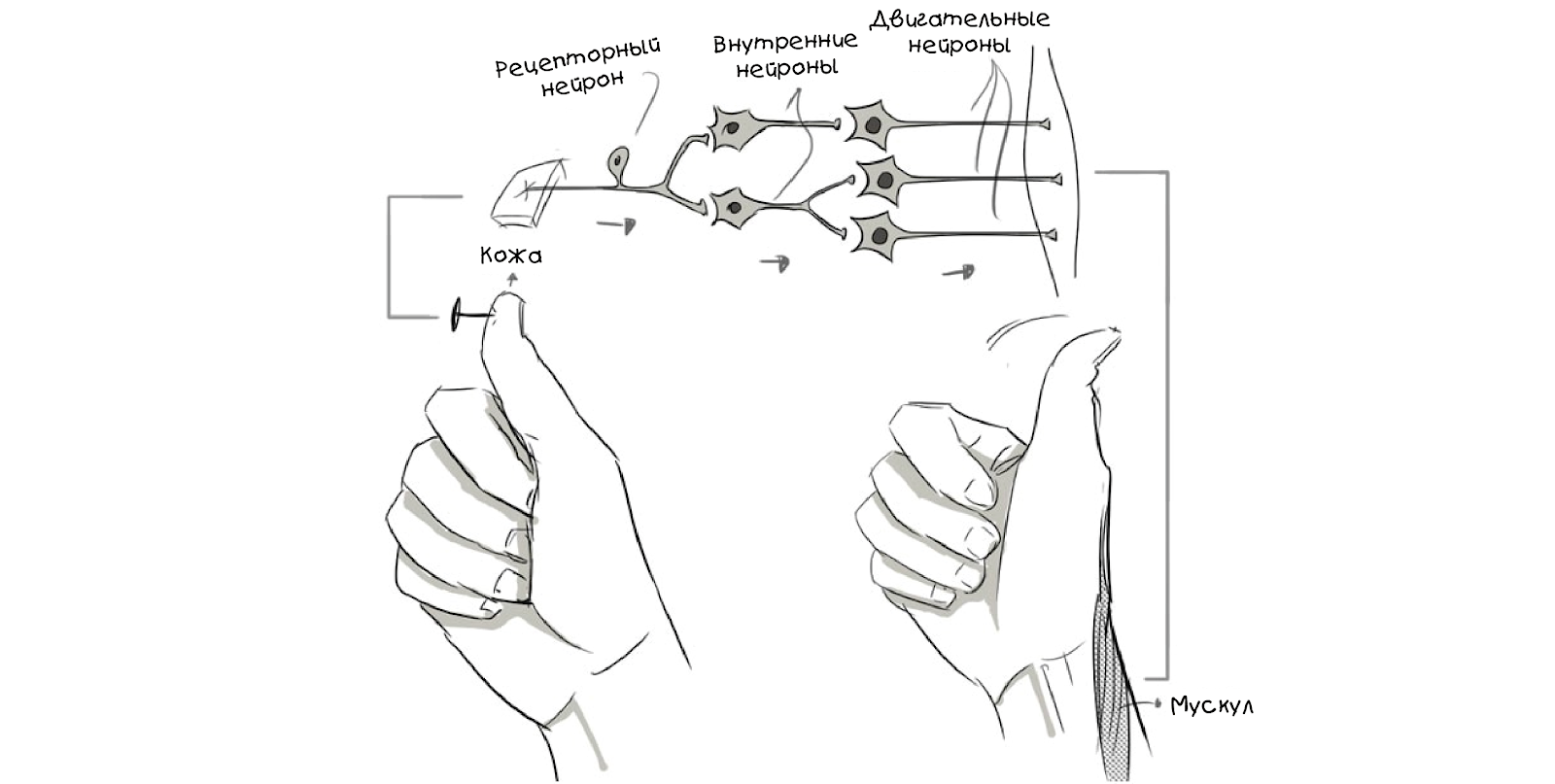
और ग्राफ का उपयोग करके औपचारिक रूप से इसका वर्णन करें:



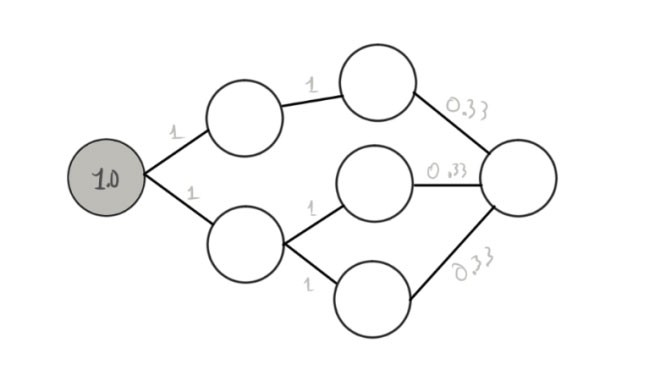
यहाँ कुछ स्पष्टीकरण आवश्यक है। मंडलियां न्यूरॉन्स हैं, और लाइनें उनके बीच संबंध हैं,
और, इस स्तर पर जटिल नहीं होने के कारण, रिश्ते को बाएं से दाएं की जानकारी का एक सीधा आंदोलन है। पहला न्यूरॉन वर्तमान में सक्रिय और धूसर है। हमने उसे एक नंबर भी सौंपा (1 - यदि यह काम करता है, तो 0 - यदि नहीं)। न्यूरॉन्स के बीच की संख्या कनेक्शन के वजन का संकेत देती है।

ऊपर दिए गए ग्राफ़ नेटवर्क के समय के क्षण को दिखाते हैं, अधिक सटीक प्रदर्शन के लिए, आपको इसे समय अवधि में विभाजित करने की आवश्यकता है:



अपना खुद का न्यूरल नेटवर्क बनाने के लिए, आपको यह समझने की जरूरत है कि वज़न न्यूरॉन्स को कैसे प्रभावित करते हैं और न्यूरॉन्स कैसे प्रशिक्षित होते हैं। एक उदाहरण के रूप में, एक खरगोश (परीक्षण खरगोश) लें और इसे एक शास्त्रीय प्रयोग की शर्तों में डालें।



जब हवा की एक सुरक्षित धारा उन पर निर्देशित होती है, तो खरगोश, जैसे लोग, झपकी लेते हैं:



यह व्यवहार मॉडल रेखांकन किया जा सकता है:



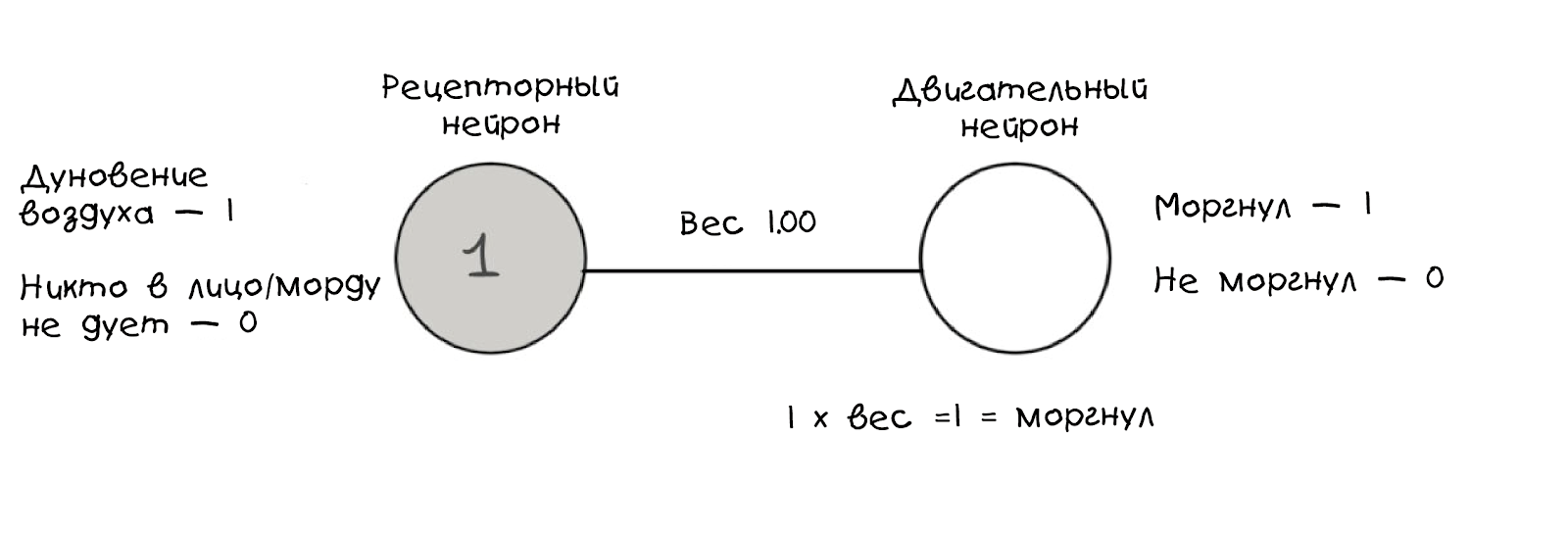
पिछले आरेख की तरह, ये रेखांकन केवल उस क्षण को दिखाते हैं जब खरगोश एक सांस महसूस करता है, और इस तरह से हम एक तार्किक मान के रूप में झटका कोड करते हैं । इसके अलावा, हम गणना करते हैं कि वजन मूल्य के आधार पर दूसरा न्यूरॉन ट्रिगर है या नहीं। यदि यह 1 है, तो संवेदी न्यूरॉन को ट्रिगर किया जाता है, हम झपकी लेते हैं; यदि वजन 1 से कम है, तो हम पलक नहीं झपकाते हैं: दूसरे न्यूरॉन की सीमा 1 है।

हम एक और तत्व का परिचय देते हैं - एक सुरक्षित ध्वनि संकेत:



हम खरगोश के हित को निम्नानुसार मॉडल कर सकते हैं:



मुख्य अंतर यह है कि अब वजन शून्य है , इसलिए हमें कम से कम अब के लिए एक निमिष खरगोश नहीं मिला है। अब खरगोश को टीम पर ब्लिंक करना, मिक्स करना सिखाएं
अड़चन (ध्वनि संकेत और सांस):



यह महत्वपूर्ण है कि ये घटनाएं अलग-अलग समय अवधि में होती हैं, रेखांकन में यह इस तरह दिखेगा:



ध्वनि स्वयं कुछ नहीं करती है, लेकिन एयरफ्लो अभी भी खरगोश को झपकी देता है, और हम इसे उत्तेजनाओं (लाल) से गुणा वजन के माध्यम से दिखाते हैं।

जटिल व्यवहार के बारे में सीखना समय के साथ जुड़े न्यूरॉन्स के बीच वजन में एक क्रमिक परिवर्तन के रूप में सरल रूप से व्यक्त किया जा सकता है।

खरगोश को प्रशिक्षित करने के लिए, चरणों को दोहराएं:



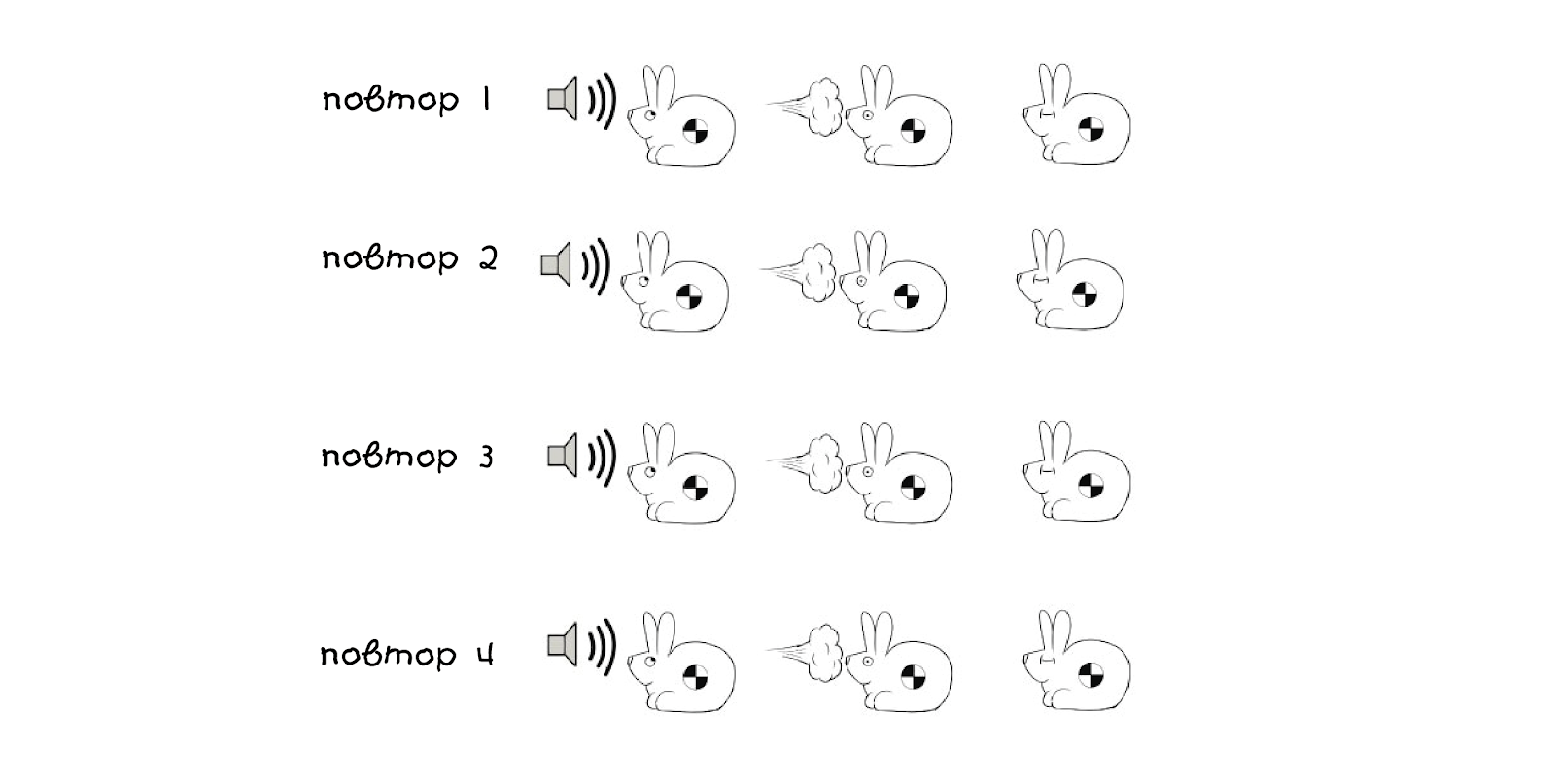
पहले तीन प्रयासों के लिए, योजनाएं इस तरह दिखाई देंगी:



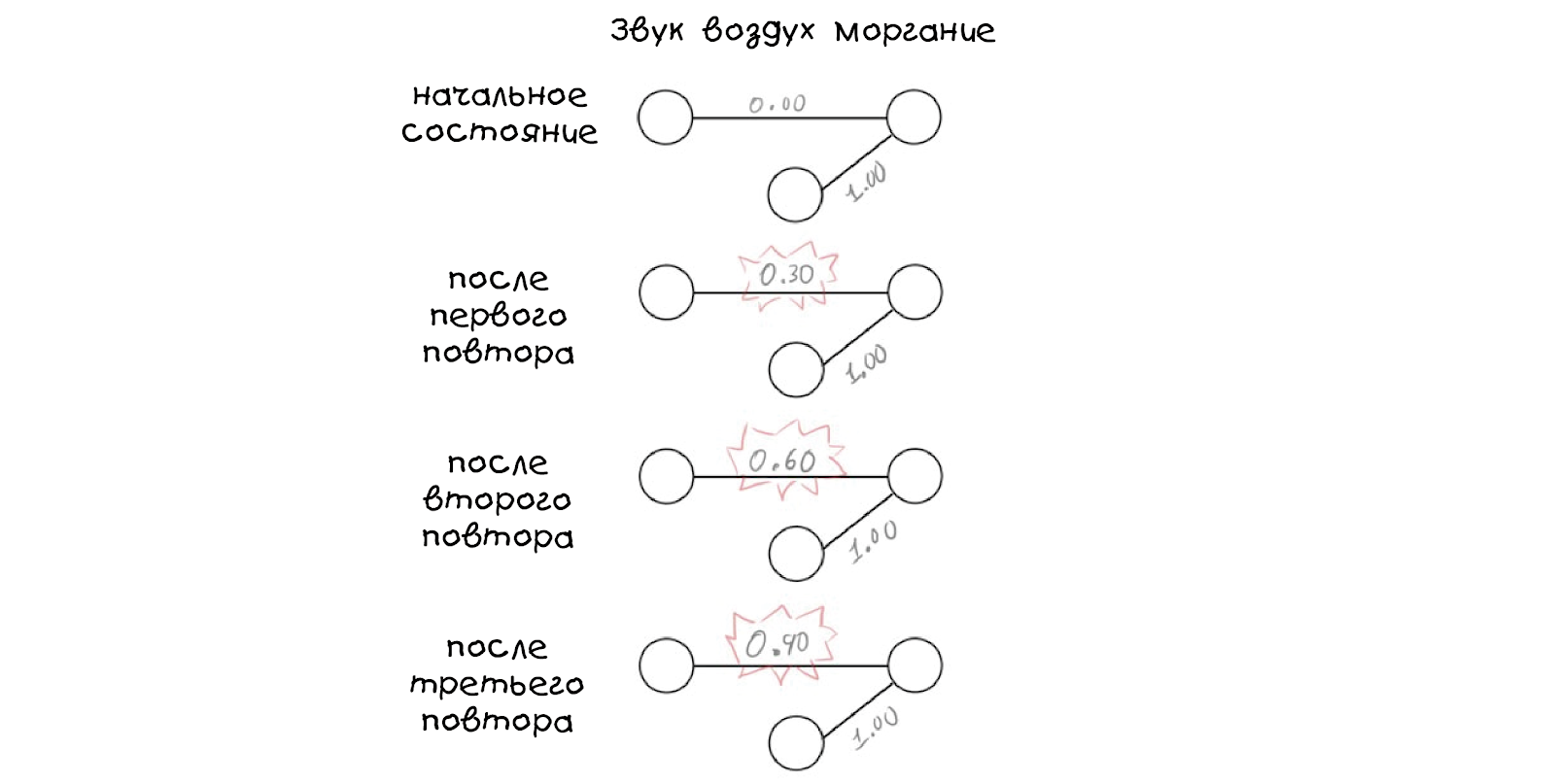
कृपया ध्यान दें कि ध्वनि उत्तेजना के लिए वजन प्रत्येक पुनरावृत्ति (लाल रंग में हाइलाइट) के बाद बढ़ता है, यह मान अब मनमाना है - हमने 0.30 चुना, लेकिन संख्या कुछ भी हो सकती है, यहां तक ​​कि नकारात्मक भी। तीसरे पुनरावृत्ति के बाद, आप खरगोश के व्यवहार में बदलाव पर ध्यान नहीं देंगे, लेकिन चौथे पुनरावृत्ति के बाद कुछ आश्चर्यजनक होगा - व्यवहार बदल जाएगा।



हमने हवा से प्रभाव को हटा दिया, लेकिन जब उसने एक बीप सुना तो खरगोश अभी भी झपकी ले रहा है! यह अंतिम व्यवहार इस व्यवहार की व्याख्या कर सकता है:



हमने खरगोश को निमिष द्वारा ध्वनि का जवाब देने के लिए प्रशिक्षित किया।


इस तरह के एक वास्तविक प्रयोग में, परिणाम प्राप्त करने के लिए 60 से अधिक पुनरावृत्ति की आवश्यकता हो सकती है।

अब हम मस्तिष्क और खरगोशों की जैविक दुनिया को छोड़ देंगे और हर चीज को अपने अनुकूल बनाने की कोशिश करेंगे
एक कृत्रिम तंत्रिका नेटवर्क बनाना सीखा। पहले, एक सरल कार्य करने की कोशिश करते हैं।

मान लीजिए कि हमारे पास चार बटन वाली एक मशीन है जो दाईं ओर दबाने पर भोजन देती है
बटन (अच्छी तरह से, या ऊर्जा यदि आप एक रोबोट हैं)। कार्य यह पता लगाना है कि कौन सा बटन इनाम देता है:



हम चित्रण कर सकते हैं (योजनाबद्ध रूप से) बटन क्या करता है जब निम्नानुसार क्लिक किया जाता है:



यह समस्या पूरी तरह से हल हो गई है, तो आइए सभी संभावित परिणामों को देखें, जिसमें सही एक भी शामिल है:


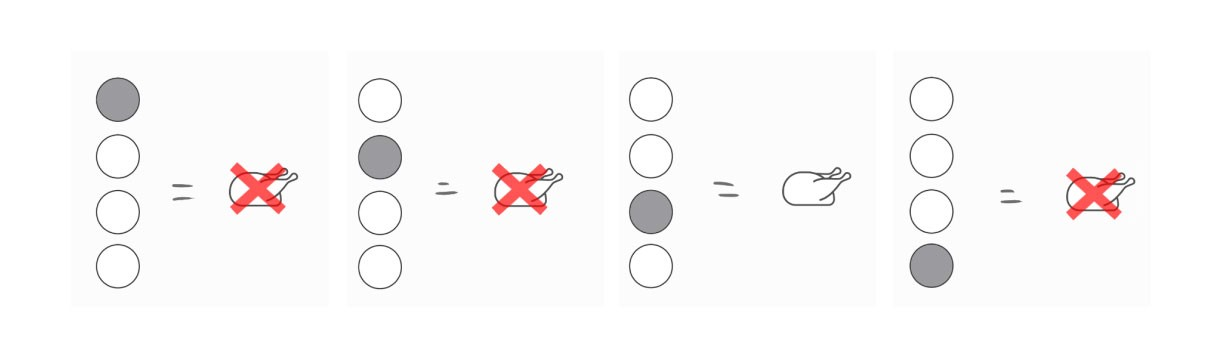अपने रात्रिभोज को प्राप्त करने के लिए 3 बटन दबाएं।

कोड में एक तंत्रिका नेटवर्क को पुन: पेश करने के लिए, हमें पहले एक मॉडल या ग्राफ बनाने की आवश्यकता होती है जिसके साथ नेटवर्क जुड़ा हो सकता है। यहां एक ग्राफ कार्य के लिए उपयुक्त है, इसके अलावा, यह अपने जैविक समकक्ष को अच्छी तरह से प्रदर्शित करता है:



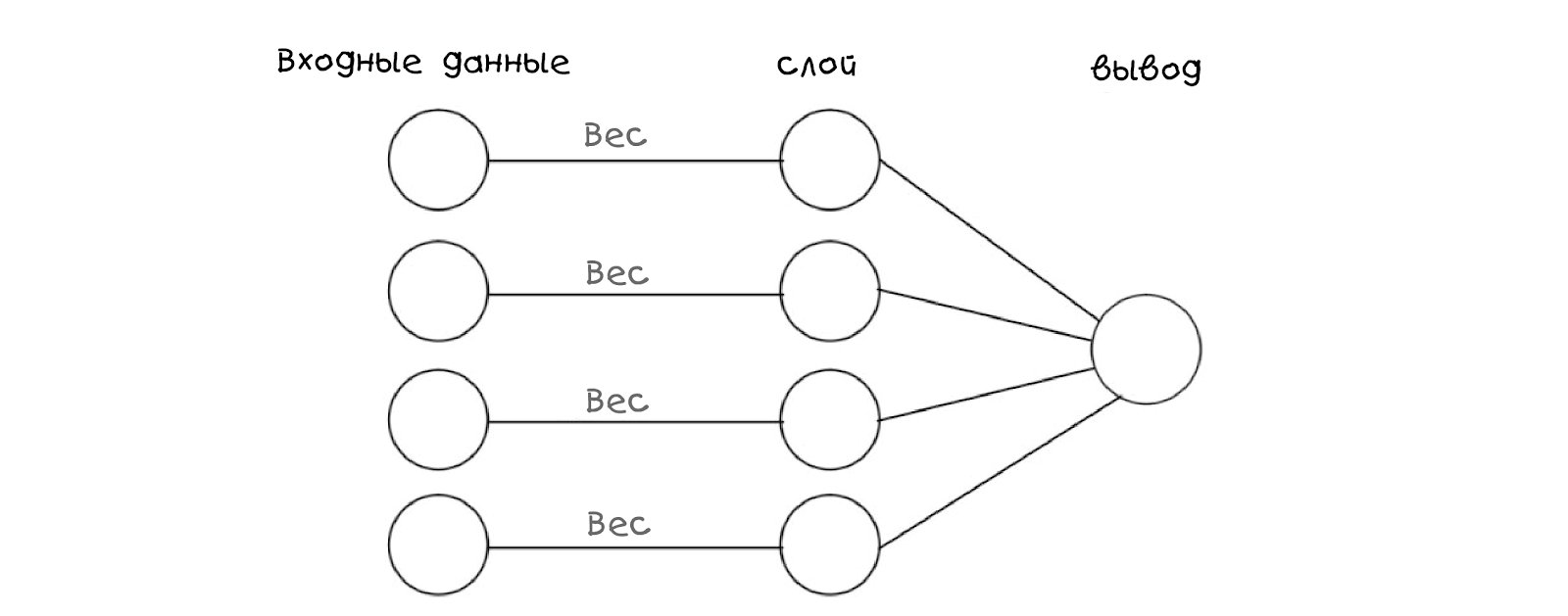
यह तंत्रिका नेटवर्क केवल आने वाली जानकारी प्राप्त करता है - इस मामले में यह धारणा होगी कि किस बटन को दबाया गया था। इसके अलावा, नेटवर्क वज़न के साथ आने वाली सूचनाओं को बदल देता है और एक परत के अतिरिक्त के आधार पर निष्कर्ष निकालता है। यह थोड़ा भ्रमित करने वाला लगता है, लेकिन आइए देखें कि हमारे मॉडल में बटन कैसे प्रस्तुत किया गया है:


ध्यान दें कि सभी भार 0 हैं, इसलिए शिशु नेटवर्क, एक शिशु की तरह, पूरी तरह से खाली है, लेकिन पूरी तरह से परस्पर जुड़ा हुआ है।

इस प्रकार, हम बाह्य घटना की तुलना तंत्रिका नेटवर्क की इनपुट परत के साथ करते हैं और इसके आउटपुट पर मूल्य की गणना करते हैं। यह वास्तविकता के साथ मेल खा सकता है या नहीं, लेकिन अभी के लिए हम इसे अनदेखा करेंगे और कंप्यूटर के अनुकूल तरीके से कार्य का वर्णन करना शुरू करेंगे। चलो वजन दर्ज करके शुरू करते हैं (हम जावास्क्रिप्ट का उपयोग करेंगे):

var inputs = [0,1,0,0]; var weights = [0,0,0,0]; //       

अगला कदम एक फ़ंक्शन बनाना है जो इनपुट मान और वजन एकत्र करता है और आउटपुट पर मूल्य की गणना करता है:

 function evaluateNeuralNetwork(inputVector, weightVector){ var result = 0; inputVector.forEach(function(inputValue, weightIndex) { layerValue = inputValue*weightVector[weightIndex]; result += layerValue; }); return (result.toFixed(2)); } //   ,  ,    —    /    

जैसा कि अपेक्षित था, यदि हम इस कोड को चलाते हैं, तो हमें अपने मॉडल या ग्राफ़ के समान परिणाम प्राप्त होगा ...

 evaluateNeuralNetwork(inputs, weights); // 0.00 

लाइव उदाहरण: तंत्रिका शुद्ध 001 ।

हमारे तंत्रिका नेटवर्क को बेहतर बनाने का अगला कदम वास्तविक स्थिति के मुकाबले अपने स्वयं के आउटपुट या परिणाम मूल्यों की जांच करने का एक तरीका होगा,
आइए पहले इस विशेष वास्तविकता को एक चर में कूटबद्ध करें:



विसंगतियों (और कितने) का पता लगाने के लिए, हम एक त्रुटि फ़ंक्शन जोड़ते हैं:

 Error = Reality - Neural Net Output 

इसके साथ, हम अपने तंत्रिका नेटवर्क के प्रदर्शन का मूल्यांकन कर सकते हैं:



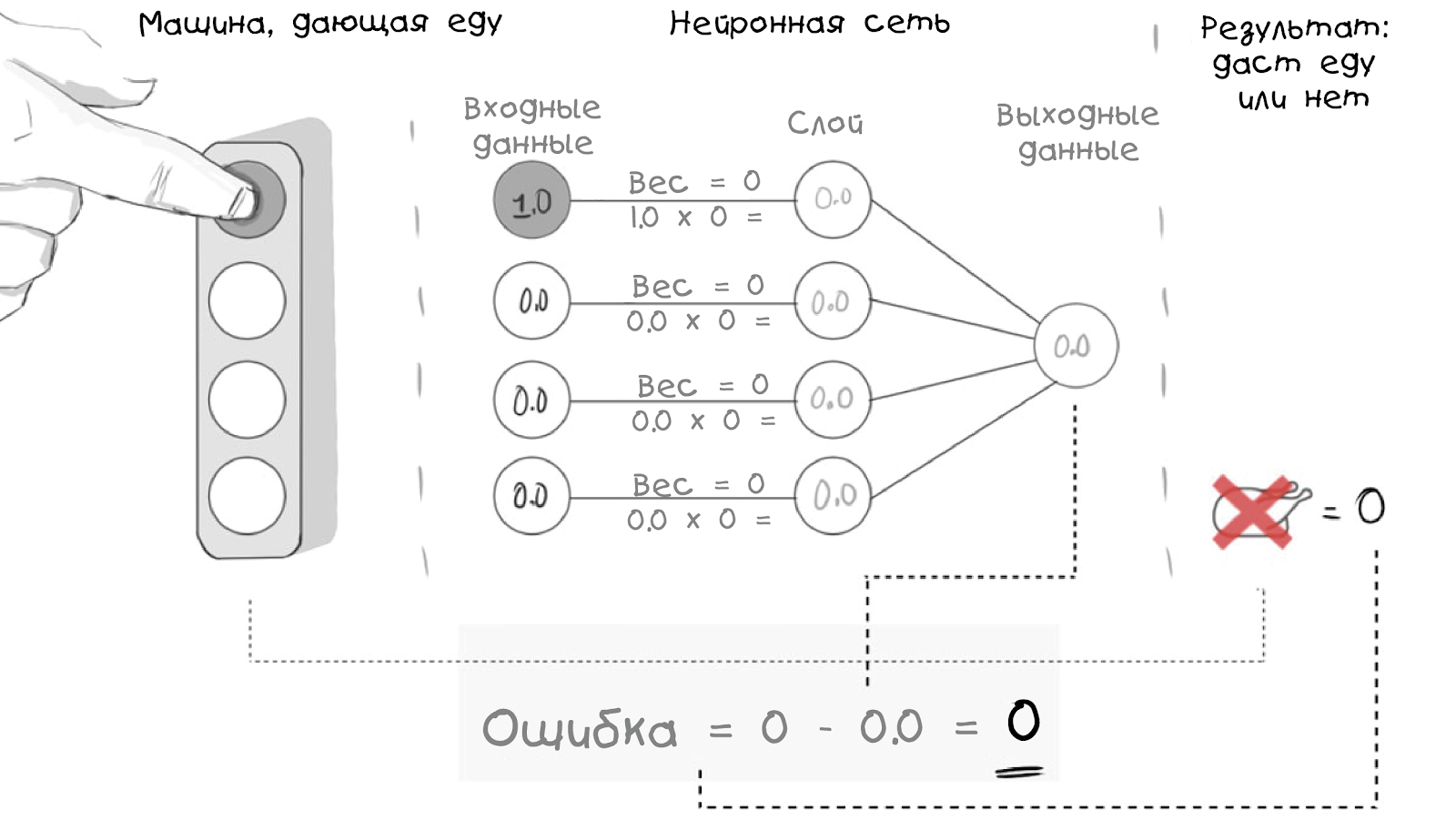
लेकिन इससे भी महत्वपूर्ण बात यह है कि उन स्थितियों के बारे में क्या है जहां वास्तविकता सकारात्मक परिणाम देती है?



अब हम जानते हैं कि हमारा तंत्रिका नेटवर्क मॉडल काम नहीं करता है (और हम जानते हैं कि कितना है), महान! यह बहुत अच्छा है क्योंकि अब हम अपने सीखने को नियंत्रित करने के लिए त्रुटि फ़ंक्शन का उपयोग कर सकते हैं। लेकिन यह सब समझ में आता है अगर हम त्रुटि समारोह को फिर से परिभाषित करते हैं:

 Error = <b>Desired Output</b> - Neural Net Output 

एक मायावी, लेकिन इस तरह की एक महत्वपूर्ण विसंगति, शांति से दिखा रहा है कि हम करेंगे
भविष्य के कार्यों के साथ तुलना करने के लिए पहले प्राप्त परिणामों का उपयोग करें
(और प्रशिक्षण के लिए, जैसा कि हम बाद में देखेंगे)। यह वास्तविक जीवन में मौजूद है, से भरा हुआ है
दोहराए जाने वाले पैटर्न, इसलिए यह एक विकासवादी रणनीति (अच्छी तरह से, में) बन सकती है
ज्यादातर मामले)।

अगला, हमारे नमूना कोड में, हम एक नया चर जोड़ेंगे:

 var input = [0,0,1,0]; var weights = [0,0,0,0]; var desiredResult = 1; 

और एक नई सुविधा:

 function evaluateNeuralNetError(desired,actual) { return (desired — actual); } // After evaluating both the Network and the Error we would get: // "Neural Net output: 0.00 Error: 1" 

लाइव उदाहरण: तंत्रिका शुद्ध 002 ।

सबटोटल को संक्षेप में प्रस्तुत करना । हमने कार्य के साथ शुरू किया, एक जैविक तंत्रिका नेटवर्क के रूप में इसका सरल मॉडल बनाया, और वास्तविकता या वांछित परिणाम की तुलना में इसके प्रदर्शन को मापने का एक तरीका मिला। अब हमें विसंगति को दूर करने का एक तरीका खोजने की जरूरत है - एक ऐसी प्रक्रिया जिसे कंप्यूटर और लोगों दोनों के लिए एक प्रशिक्षण माना जा सकता है।

कैसे एक तंत्रिका नेटवर्क को प्रशिक्षित करने के लिए?

जैविक और कृत्रिम दोनों तंत्रिका नेटवर्क को पढ़ाने का आधार पुनरावृत्ति है
और प्रशिक्षण एल्गोरिदम , इसलिए हम उनके साथ अलग से काम करेंगे। से शुरू करें
एल्गोरिदम सीखना।

प्रकृति में, सीखने के एल्गोरिदम को भौतिक या रासायनिक में परिवर्तन के रूप में समझा जाता है
प्रयोगों के बाद न्यूरॉन्स की विशेषताएं:



कोड में समय के साथ दो न्यूरॉन्स कैसे बदलते हैं और हमारे मॉडल "लर्निंग एल्गोरिथम" का एक नाटकीय चित्रण का मतलब है कि हम अपने जीवन को आसान बनाने के लिए समय के साथ कुछ बदल देंगे। इसलिए, आइए जीवन की सुविधा की डिग्री को इंगित करने के लिए एक चर जोड़ें:

 var learningRate = 0.20; //   ,      :) 

और यह क्या बदलेगा?

यह वजन को बदल देगा (बस एक खरगोश की तरह!), विशेष रूप से हमारे द्वारा वांछित आउटपुट का वजन:



इस तरह के एक एल्गोरिथ्म को कैसे कोड किया जाए यह आपकी पसंद है, सादगी के लिए मैं प्रशिक्षण गुणांक को वजन में जोड़ता हूं, यहां यह एक फ़ंक्शन के रूप में है:

 function learn(inputVector, weightVector) { weightVector.forEach(function(weight, index, weights) { if (inputVector[index] > 0) { weights[index] = weight + learningRate; } }); } 

जब उपयोग किया जाता है, तो यह सीखने का कार्य हमारे सीखने के गुणांक को सक्रिय न्यूरॉन के भार वेक्टर में जोड़ देगा, प्रशिक्षण चक्र (या पुनरावृत्ति) के पहले और बाद के परिणाम निम्नानुसार होंगे:

 // Original weight vector: [0,0,0,0] // Neural Net output: 0.00 Error: 1 learn(input, weights); // New Weight vector: [0,0.20,0,0] // Neural Net output: 0.20 Error: 0.8 //    ,      1 ( ) — ,    ,    ,       

लाइव उदाहरण: न्यूरल नेट 003 ।

ठीक है, अब जब हम सही दिशा में आगे बढ़ रहे हैं, तो इस पहेली का अंतिम विवरण दोहराव का परिचय होगा।

यह इतना मुश्किल नहीं है, प्रकृति में हम बस एक ही काम करते हैं, और कोड में हम सिर्फ दोहराव की संख्या दर्शाते हैं:

 var trials = 6; 

और हमारे प्रशिक्षण तंत्रिका नेटवर्क में पुनरावृत्ति फ़ंक्शन की संख्या की शुरूआत इस तरह दिखाई देगी:

 function train(trials) { for (i = 0; i < trials; i++) { neuralNetResult = evaluateNeuralNetwork(input, weights); learn(input, weights); } } 

खैर, हमारी अंतिम रिपोर्ट:

 Neural Net output: 0.00 Error: 1.00 Weight Vector: [0,0,0,0] Neural Net output: 0.20 Error: 0.80 Weight Vector: [0,0,0.2,0] Neural Net output: 0.40 Error: 0.60 Weight Vector: [0,0,0.4,0] Neural Net output: 0.60 Error: 0.40 Weight Vector: [0,0,0.6,0] Neural Net output: 0.80 Error: 0.20 Weight Vector: [0,0,0.8,0] Neural Net output: 1.00 Error: 0.00 Weight Vector: [0,0,1,0] // Chicken Dinner ! 

लाइव उदाहरण: न्यूरल नेट 004 ।

अब हमारे पास एक वजन वेक्टर है जो केवल एक परिणाम देगा (रात के खाने के लिए चिकन), अगर इनपुट वेक्टर वास्तविकता से मेल खाता है (तीसरे बटन को दबाकर)।

तो क्या कूल हैं हम बस?

इस विशेष मामले में, हमारे तंत्रिका नेटवर्क (प्रशिक्षण के बाद) इनपुट डेटा को पहचान सकते हैं और कह सकते हैं कि वांछित परिणाम क्या होगा (हमें अभी भी विशिष्ट परिस्थितियों को प्रोग्राम करने की आवश्यकता है):



इसके अलावा, यह हमारे प्रशिक्षण के लिए एक स्केलेबल मॉडल, खिलौना और उपकरण है। हम मशीन सीखने, तंत्रिका नेटवर्क और कृत्रिम बुद्धि के बारे में कुछ नया सीखने में सक्षम थे।

उपयोगकर्ताओं को सावधानी:

• अध्ययन किए गए तराजू के लिए एक भंडारण तंत्र प्रदान नहीं किया जाता है, इसलिए यह तंत्रिका नेटवर्क वह सब कुछ भूल जाएगा जो यह जानता है। कोड को अपडेट या रीस्टार्ट करते समय, आपको कम से कम छह सफल रीट्रीज की आवश्यकता होती है ताकि नेटवर्क पूरी तरह से प्रशिक्षित हो जाए अगर आपको लगता है कि कोई व्यक्ति या मशीन यादृच्छिक रूप से बटन दबाएगा ... इसमें कुछ समय लगेगा।
  
• महत्वपूर्ण चीजों को सीखने के लिए जैविक नेटवर्क में सीखने की गति 1 है, इसलिए आपको केवल एक सफल दोहराने की आवश्यकता है।
  
• एक सीखने का एल्गोरिथ्म है जो जैविक न्यूरॉन्स के समान है, इसका एक आकर्षक नाम है: वाइड्रॉफ-हॉफ नियम , या विड्रॉफ-हॉफ प्रशिक्षण ।
  
• न्यूरॉन्स के थ्रेशोल्ड्स (हमारे उदाहरण में 1) और रिट्रेनिंग के प्रभाव (बड़ी संख्या में पुनरावृत्ति के साथ, परिणाम 1 से अधिक होगा) को ध्यान में नहीं रखा जाता है, लेकिन वे प्रकृति में बहुत महत्वपूर्ण हैं और व्यवहार प्रतिक्रियाओं के बड़े और जटिल ब्लॉकों के लिए जिम्मेदार हैं। नकारात्मक भार की तरह।
  

नोट्स और आगे पढ़ने के लिए संदर्भ

मैंने गणित और सख्त शब्दों से बचने की कोशिश की, लेकिन अगर आप रुचि रखते हैं, तो हमने एक पेसेप्ट्रॉन का निर्माण किया, जिसे दोहरे क्लासिफायर के पर्यवेक्षित शिक्षण ( शिक्षक के साथ शिक्षण ) के लिए एक एल्गोरिथ्म के रूप में परिभाषित किया गया है - एक कठिन चीज।

मस्तिष्क की जैविक संरचना एक साधारण विषय नहीं है, आंशिक रूप से अशुद्धि के कारण, आंशिक रूप से इसकी जटिलता के कारण। यह तंत्रिका विज्ञान (Purves) और संज्ञानात्मक तंत्रिका विज्ञान (Gazzaniga) के साथ शुरू करना सबसे अच्छा है। मैंने गेटवे से मेमोरी (ग्लक) तक खरगोश के उदाहरण को संशोधित और अनुकूलित किया, जो ग्राफ की दुनिया के लिए एक महान मार्गदर्शक भी है।

एक और भव्य संसाधन, एन इंट्रोडक्शन टू न्यूरल नेटवर्क्स (गुरनी), आपके सभी एआई-संबंधित जरूरतों के लिए उपयुक्त है।

और अब पायथन में! प्रदान किए गए पायथन संस्करण के लिए इलिया एन्डस्मिड्ट का धन्यवाद:

 inputs = [0, 1, 0, 0] weights = [0, 0, 0, 0] desired_result = 1 learning_rate = 0.2 trials = 6 def evaluate_neural_network(input_array, weight_array): result = 0 for i in range(len(input_array)): layer_value = input_array[i] * weight_array[i] result += layer_value print("evaluate_neural_network: " + str(result)) print("weights: " + str(weights)) return result def evaluate_error(desired, actual): error = desired - actual print("evaluate_error: " + str(error)) return error def learn(input_array, weight_array): print("learning...") for i in range(len(input_array)): if input_array[i] > 0: weight_array[i] += learning_rate def train(trials): for i in range(trials): neural_net_result = evaluate_neural_network(inputs, weights) learn(inputs, weights) train(trials) 

और अब जाओ! किरन मैहर के इस संस्करण के लिए धन्यवाद।

 package main import ( "fmt" "math" ) func main() { fmt.Println("Creating inputs and weights ...") inputs := []float64{0.00, 0.00, 1.00, 0.00} weights := []float64{0.00, 0.00, 0.00, 0.00} desired := 1.00 learningRate := 0.20 trials := 6 train(trials, inputs, weights, desired, learningRate) } func train(trials int, inputs []float64, weights []float64, desired float64, learningRate float64) { for i := 1; i < trials; i++ { weights = learn(inputs, weights, learningRate) output := evaluate(inputs, weights) errorResult := evaluateError(desired, output) fmt.Print("Output: ") fmt.Print(math.Round(output*100) / 100) fmt.Print("\nError: ") fmt.Print(math.Round(errorResult*100) / 100) fmt.Print("\n\n") } } func learn(inputVector []float64, weightVector []float64, learningRate float64) []float64 { for index, inputValue := range inputVector { if inputValue > 0.00 { weightVector[index] = weightVector[index] + learningRate } } return weightVector } func evaluate(inputVector []float64, weightVector []float64) float64 { result := 0.00 for index, inputValue := range inputVector { layerValue := inputValue * weightVector[index] result = result + layerValue } return result } func evaluateError(desired float64, actual float64) float64 { return desired - actual }