🤴🏿 🤜🏻 👨‍👧 एक गगनचुंबी इमारत और अंडे के साथ एक कार्य

वास्तव में, वह सबसे अधिक है। लेकिन पहले बातें पहले।

समस्या का बयान

मैं अजगर को मास्टर करता हूं, कोडवर्ड पर सब कुछ हल करता हूं। मैं एक गगनचुंबी इमारत और अंडे के बारे में एक प्रसिद्ध कार्य का सामना करता हूं। अंतर केवल इतना है कि स्रोत डेटा 100 मंजिल और 2 अंडे नहीं है, लेकिन थोड़ा अधिक है।
यह देखते हुए: एन अंडे, एम उन्हें फेंकने का प्रयास करता है, अंतहीन गगनचुंबी इमारत।

परिभाषित करें: अधिकतम मंजिल जिससे आप बिना टूटे एक अंडा फेंक सकते हैं। अंडे एक निर्वात में गोलाकार होते हैं और, यदि उनमें से एक 99 वीं मंजिल से, उदाहरण के लिए, टूटना, गिरना नहीं होता है, तो दूसरे भी सौवीं से कम सभी मंजिलों से गिरने का सामना करेंगे।

0 <= एन, एम <= 20,000।
दो दर्जन परीक्षणों का रन समय 12 सेकंड है।

समाधान के लिए खोजें

हमें एक फ़ंक्शन ऊंचाई (एन, एम) लिखने की आवश्यकता है, जो दिए गए एन, एम के लिए फर्श संख्या वापस कर देगी। चूंकि यह बहुत बार उल्लेख किया जाएगा, और हर बार जब आप "ऊंचाई" आलस्य लिखते हैं, तो कोड के अलावा हर जगह मैं इसे च (एन, एम) के रूप में नामित करूंगा।

शुरुआत करते हैं शून्य से। जाहिर है, अगर अंडे नहीं हैं या उन्हें फेंकने का प्रयास नहीं है, तो कुछ भी निर्धारित नहीं किया जा सकता है और जवाब शून्य होगा। f (0, m) = 0, f (n, 0) = 0।

मान लीजिए कि एक अंडा है, और 10 प्रयास हैं। आप सब कुछ जोखिम में डाल सकते हैं और इसे ठीक सौवीं मंजिल से दूर फेंक सकते हैं, लेकिन विफलता के मामले में, आप कुछ और निर्धारित नहीं कर पाएंगे, इसलिए पहली मंजिल से शुरू करना और प्रत्येक फेंक के बाद एक मंजिल पर जाना अधिक तर्कसंगत है। जब तक या तो प्रयास या अंडा समाप्त नहीं हो जाता। अधिकतम जहां आप प्राप्त कर सकते हैं यदि अंडा विफल नहीं होता है मंजिल संख्या 10. एफ (1, एम) = एम

दूसरा अंडा लें, फिर से प्रयास करें। अब, फिर आप एक सौवां मौका ले सकते हैं? यदि यह टूटता है, तो एक और अधिक और 9 प्रयास होंगे, कम से कम 9 मंजिलें गुजर सकेंगी। तो शायद आपको सौवें से नहीं, बल्कि दसवें से जोखिम उठाने की आवश्यकता है? तार्किक है। फिर, यदि सफल, 2 अंडे और 9 प्रयास रहेंगे। सादृश्य से, अब आपको एक और 9 मंजिलों तक जाने की आवश्यकता है। सफलताओं की एक श्रृंखला के साथ - एक और 8, 7, 6, 5, 4, 3, 2 और 1. कुल, हम दो पूरे अंडे के साथ और बिना कोशिश किए 55 वीं मंजिल पर हैं। उत्तर पहले सदस्य 1 और चरण 1. च (2, मी) = (एम * एम + एम) / 2 के साथ अंकगणितीय प्रगति के पहले एम सदस्यों का योग है। यह भी स्पष्ट है कि प्रत्येक चरण में फ़ंक्शन f (1, m) को बुलाया गया था, लेकिन यह अभी तक सटीक नहीं है।

तीन अंडे और दस प्रयासों के साथ जारी रखें। असफल पहले फेंकने की स्थिति में, 2 अंडों से ढकी हुई मंजिलें और 9 प्रयास नीचे से आच्छादित होंगे, जिसका अर्थ है कि पहला फेंक फर्श से बनाया जाना चाहिए f (2, 9) + 1. फिर, यदि सफल हो, तो हमारे पास 3 अंडे और 9 प्रयास हैं। । और दूसरे प्रयास के लिए आपको एक और f (2.8) + 1 मंजिल तक जाने की आवश्यकता है। और इसी तरह, जब तक 3 अंडे और 3 प्रयास हाथों पर रहते हैं। और फिर एन = एम के साथ मामलों पर विचार करके विचलित होने का समय है, जब प्रयास के रूप में कई अंडे हैं।

और उसी समय जब अधिक अंडे होते हैं।

लेकिन यहां सब कुछ स्पष्ट है - उन लोगों से परे अंडे जो तोड़ने के लिए हमारे लिए उपयोगी नहीं होंगे, भले ही हर फेंक असफल हो। f (n, m) = f (m, m) यदि n> m और सभी में, 3 अंडे, 3 फेंकता है। यदि पहला अंडा टूटता है, तो आप नीचे तक f (2, 2) फर्श की जांच कर सकते हैं, और अगर यह नहीं टूटता है, तो शीर्ष पर f (3,2) फर्श, यानी एक ही f (2, 2)। कुल एफ (3, 3) = 2 * एफ (2, 2) + 1 = 7. और एफ (4, 4), सादृश्य द्वारा, दो एफ (3, 3) और एक से मिलकर होगा, और यह होगा 15. सभी यह दो की शक्तियों जैसा दिखता है, और हम लिखते हैं: f (m, m) = 2 ^ m - 1 ।

यह भौतिक दुनिया में एक द्विआधारी खोज की तरह दिखता है: हम मंजिल नंबर 2 ^ (m-1) से शुरू करते हैं, सफलता के मामले में हम 2 ^ (m-2) ऊपर जाते हैं, और विफलता के मामले में, हम बहुत नीचे जाते हैं, और इसलिए जब तक प्रयास खत्म नहीं हो जाते। हमारे मामले में, हम हर समय उठते हैं।

चलो वापस एफ (3, 10) पर जाएं। वास्तव में, प्रत्येक चरण पर, यह सभी सम f (2, m-1) के नीचे आता है - विफलता की स्थिति में निर्धारित की जा सकने वाली मंजिलों की संख्या, इकाइयों और f (3, m-1) - सफलता की स्थिति में निर्धारित की जा सकने वाली मंजिलों की संख्या। और यह स्पष्ट हो जाता है कि अंडे की संख्या में वृद्धि और प्रयासों से यह संभावना नहीं है कि कुछ भी बदल जाएगा। f (n, m) = f (n - 1, m - 1) + 1 + f (n, m - 1) । और यह एक सार्वभौमिक सूत्र है जिसे कोड में लागू किया जा सकता है।

from functools import lru_cache @lru_cache() def height(n,m): if n==0 or m==0: return 0 elif n==1: return m elif n==2: return (m**2+m)/2 elif n>=m: return 2**n-1 else: return height(n-1,m-1)+1+height(n,m-1)

बेशक, पहले मैंने गैर-ज्ञापन पुनरावर्ती कार्यों की खातिर कदम रखा और पता चला कि एफ (10, 40) कॉल की संख्या के साथ लगभग 40 सेकंड लेता है - 97806983. लेकिन संस्मरण भी प्रारंभिक अंतराल पर ही बचाता है। यदि f (200,400) 0.8 सेकंड में निष्पादित होता है, तो f (200, 500) पहले से ही 31 सेकंड में है। यह हास्यास्पद है कि% समयसीमा का उपयोग करके रनटाइम को मापते समय, परिणाम वास्तविक से बहुत कम होता है। जाहिर है, फ़ंक्शन का पहला रन अधिकांश समय लेता है, जबकि बाकी बस इसके ज्ञापन के परिणामों का उपयोग करते हैं। झूठ, ज़बरदस्त झूठ और आंकड़े।

पुनरावृत्ति की आवश्यकता नहीं है, हम आगे देखते हैं

इसलिए, परीक्षणों में, उदाहरण के लिए, f (9477, 10000) दिखाई देता है, लेकिन मेरी दयनीय f (200, 500) अब सही समय पर फिट नहीं होती है। तो एक और उपाय है, बिना पुनरावृत्ति के, हम इसकी खोज जारी रखेंगे। मैंने कुछ मापदंडों के साथ फ़ंक्शन कॉल की गिनती करके कोड को पूरक किया, ताकि यह देखने के लिए कि आखिरकार इसमें विघटित हो गया है। 10 प्रयासों के लिए, निम्नलिखित परिणाम प्राप्त हुए:

f (3.10) = 7+ 1 * f (2.9) + 1 * f (2.8) + 1 * f (2.7) + 1 * f (2.6) + 1 * f (2) , 5) + 1 * f (2,4) + 1 * f (2,3) + 1 * f (3,3)
f (4.10) = 27+ 1 * f (2.8) + 2 * f (2.7) + 3 * f (2.6) + 4 * f (2.5) + 5 * f (2) , 4) + 6 * f (2,3) + 6 * f (3,3) + 1 * f (4,4)
f (5.10) = 55+ 1 * f (2.7) + 3 * f (2.6) + 6 * f (2.5) + 10 * f (2.4) + 15 * f (2) , 3) + 15 * f (3.3) + 5 * f (4.4) + 1 * f (5.5)
f (6.10) = 69+ 1 * f (2.6) + 4 * f (2.5) + 10 * f (2.4) + 20 * f (2.3) + 20 * f (3) , 3) + 10 * f (4.4) + 4 * f (5.5) + 1 * f (6.6)
f (7,10) = 55+ 1 * f (2,5) + 5 * f (2,4) + 15 * f (2,3) + 15 * f (3,3) + 10 * f (4) , 4) + 6 * f (5.5) + 3 * f (6.6) + 1 * f (7.7)
f (8,10) = 27+ 1 * f (2,4) + 6 * f (2,3) + 6 * f (3,3) + 5 * f (4,4) + 4 * f (5) , 5) + 3 * f (6.6) + 2 * f (7.7) + 1 * f (8.8)
f (9,10) = 7+ 1 * f (2,3) + 1 * f (3,3) + 1 * f (4,4) + 1 * f (5,5) + 1 * f (6) , 6) + 1 * f (7.7) + 1 * f (8.8) + 1 * f (9.9)

कुछ नियमितता दिखाई देती है:

इन गुणांकों की सैद्धांतिक रूप से गणना की जाती है। प्रत्येक नीला शीर्ष और बाईं ओर का योग है। और वायलेट वाले एक ही नीले वाले हैं, केवल रिवर्स ऑर्डर में। आप गणना कर सकते हैं, लेकिन यह फिर से एक पुनरावृत्ति है, और इसमें मैं निराश था। सबसे अधिक संभावना है, कई (यह एक दया है कि यह मुझे नहीं है) पहले से ही इन नंबरों को सीखा है, लेकिन अब मैं अपने स्वयं के समाधान के बाद, साज़िश को रखूंगा। मैंने उन पर थूकने और दूसरी तरफ जाने का फैसला किया।

उन्होंने एक्सल खोला, फ़ंक्शन के परिणामों के साथ एक प्लेट बनाई, और पैटर्न की तलाश शुरू की। C3 = IF (C $ 2> $ B3; 2 ^ $ B3-1; C2 + B2 + 1), जहां $ 2 अंडे की संख्या (1-13) के साथ पंक्ति है, $ B प्रयासों की संख्या (1-20) के साथ कॉलम है सी 3 - दो अंडे और एक प्रयास के चौराहे पर सेल।

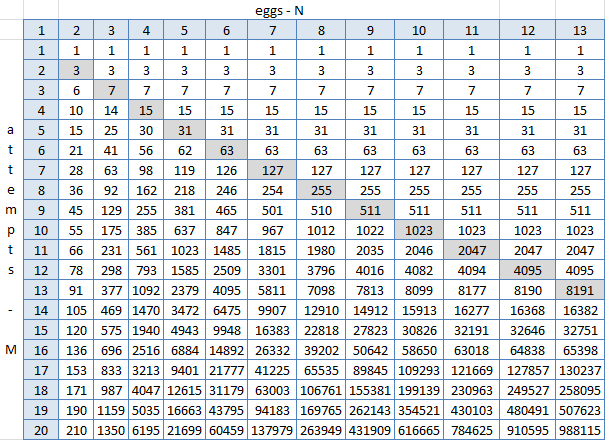
ग्रे विकर्ण एन = एम है, और यहां यह स्पष्ट रूप से दिखाई देता है कि इसके दाईं ओर (एन> एम के लिए) कुछ भी नहीं बदलता है। यह देखा जा सकता है - लेकिन यह अन्यथा नहीं हो सकता है, क्योंकि ये सभी सूत्र के कार्य के परिणाम हैं, जिसमें यह दिया गया है कि प्रत्येक कोशिका शीर्ष, शीर्ष बाएँ और एक के योग के बराबर है। लेकिन कुछ सार्वभौमिक सूत्र जहां आप एन और एम को स्थानापन्न कर सकते हैं और प्राप्त कर सकते हैं मंजिल संख्या नहीं मिली। Spoiler: यह मौजूद नहीं है। लेकिन फिर एक्सेल में यह तालिका बनाना इतना सरल है, हो सकता है कि एक ही अजगर उत्पन्न करना और उसमें से उत्तर खींचें?

तुम नहीं

मुझे याद है कि वहाँ NumPy है, जिसे सिर्फ बहुआयामी सरणियों के साथ काम करने के लिए डिज़ाइन किया गया है, क्यों नहीं इसे आज़माएं? आरंभ करने के लिए, हमें आकार N + 1 के शून्य के एक-आयामी सरणी की आवश्यकता है और आकार N की इकाइयों की एक-आयामी सरणी है। शून्य से प्रथम तत्व तक ले जाएं, इसे पहले तत्व से पहले तत्व से अंतिम तक तत्वों के साथ और इकाइयों की एक सरणी के साथ तत्वपूर्ण जोड़ें। परिणामी सरणी में, शुरुआत में शून्य जोड़ें। एम बार दोहराएं। परिणामी सरणी का तत्व संख्या N उत्तर होगा। पहले 3 चरण इस तरह दिखते हैं:

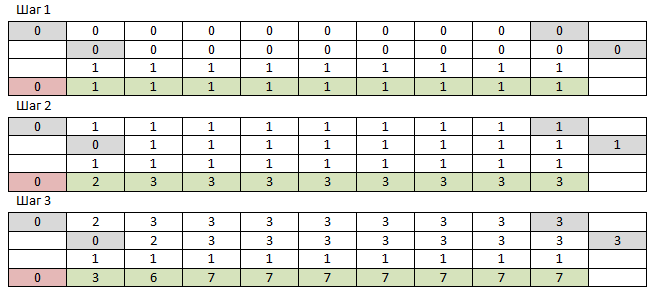
NumPy इतनी तेजी से काम करता है कि मैंने पूरी मेज को नहीं बचाया है - हर बार जब मैं आवश्यक पंक्ति को फिर से पढ़ता हूं। एक बात - बड़ी संख्या में काम करने का परिणाम गलत था। उच्च रैंक उन जैसे हैं, जबकि निचले वाले नहीं हैं। यह है कि कई परिवर्धन से संचित फ्लोटिंग-पॉइंट संख्याओं की अंकगणितीय त्रुटियां कैसी दिखती हैं। इससे कोई फर्क नहीं पड़ता - आप सरणी के प्रकार को इंट में बदल सकते हैं। नहीं, परेशानी - यह पता चला है कि गति के लिए NumPy केवल अपने डेटा प्रकारों के साथ काम करता है, और इसके int, Python int के विपरीत, 2 ^ 64-1 से अधिक नहीं हो सकता है, जिसके बाद यह चुपचाप ओवरफ्लो हो जाता है और -2 ^ 64 तक जारी रहता है। और मैं वास्तव में तीन हजार पात्रों के तहत संख्या की उम्मीद करता हूं। लेकिन यह बहुत तेजी से काम करता है, f (9477, 10000) 233 एमएस चलाता है, यह सिर्फ आउटपुट पर किसी प्रकार का बकवास करता है। मैं कोड भी नहीं दूंगा, चूंकि ऐसी बात है। मैं एक ही स्वच्छ अजगर बनाने की कोशिश करूंगा।

Iterated, iterated, लेकिन पुनरावृत्त नहीं

 def height(n, m): arr = [0]*(n+1) while m > 0: arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) m-=1 return arr[n]

F (9477, 10000) की गणना करने के लिए 44 सेकंड थोड़ा अधिक है। लेकिन बिल्कुल पक्का। क्या अनुकूलित किया जा सकता है? सबसे पहले, विकर्ण एम के अधिकार के लिए सब कुछ पर विचार करने की आवश्यकता नहीं है, एम। दूसरा - एक सेल की खातिर, आखिरी सरणी पर विचार करने के लिए। इसके लिए, पिछले एक के दो दो सेल फिट होंगे। च (10, 20) की गणना करने के लिए, केवल ये ग्रे कोशिकाएं ही पर्याप्त होंगी:

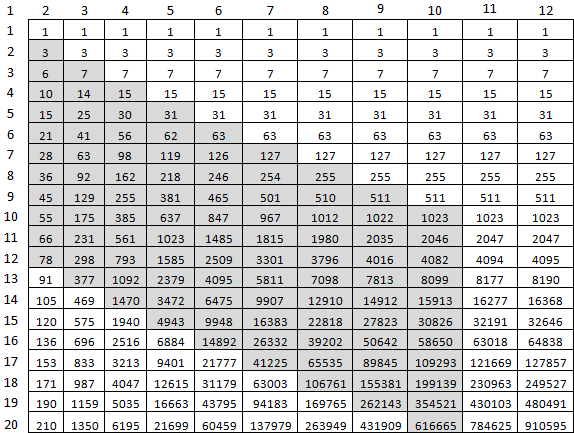
और इसलिए यह कोड में दिखता है:

 def height(n, m): arr = [0, 1, 1] i = 1 while i < n and i < mn: #    m,m arr = [0] + list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr += [arr[-1]] i+=1 arr.pop(-1) while i < n or i < mn: #        arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) arr = arr + [arr[-1]+1] if n > len(arr) else [0] + arr i+=1 while i < m: # ,     -  arr = list(map(lambda x,y: x+y+1, arr[:-1], arr[1:])) i+=1 return arr[0]

और आपको क्या लगता है? f (9477, 10000) 2 सेकंड में! लेकिन यह इनपुट बहुत अच्छा है, किसी भी स्तर पर सरणी की लंबाई 533 तत्वों (10000-9477) से अधिक नहीं होगी। चलो एफ (5477, 10000) पर जांच करें - 11 सेकंड। यह अच्छा है, लेकिन केवल 44 सेकंड की तुलना में - इस समय के साथ बीस परीक्षण पास नहीं होंगे।

ऐसा नहीं है। लेकिन चूंकि कोई कार्य है, तो एक समाधान है, खोज जारी है। मैं एक्सेल टेबल पर फिर से देखने लगा। (M, m) के बाईं ओर स्थित कोशिका हमेशा एक कम होती है। और इसके बाईं ओर सेल अब नहीं है, प्रत्येक पंक्ति में अंतर बड़ा हो जाता है। नीचे की कोशिका (m, m) हमेशा दुगुनी होती है। और इसके नीचे का सेल अब दो बार नहीं, बल्कि थोड़ा छोटा है, लेकिन प्रत्येक स्तंभ के लिए अलग-अलग, बड़ा है। और यह भी एक पंक्ति में नंबर पहली बार जल्दी से बढ़ते हैं, और धीरे-धीरे मध्य के बाद। मुझे पड़ोसी कोशिकाओं के बीच अंतर की एक तालिका बनाने दें, शायद वहां क्या पैटर्न दिखाई देगा?

वार्मर

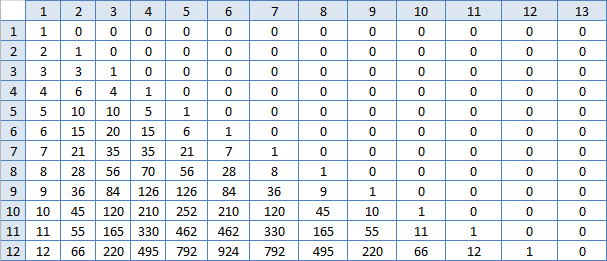
बाह, परिचित संख्या! यही है, पंक्ति संख्या M में इन संख्याओं का योग N यह उत्तर है? सच है, उन्हें गिनना लगभग उसी तरह है जैसा मैंने पहले ही किया था, यह संभावना नहीं है कि इससे काम में तेजी आएगी। लेकिन आपको प्रयास करना होगा:

f (9477, 10000): 17 सेकंड

 def height(n, m): arr = [1,1] while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) + [1] m-=1 return sum(arr[1:n+1])

या 8, यदि आप केवल आधा त्रिकोण गिनते हैं

 def height(n, m): arr = [1,1] while m > 2 and len(arr) < n+2: #    ,  n <  arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) arr += [arr[-1]] m-=2 while m > 1: arr = [1] + list(map(lambda x,y: x+y, arr[1:], arr[:-1])) m-=1 if len(arr) < n+1: arr += arr[::-1][1:] #  n   ,   return sum(arr[1:n+1])

यह कहने के लिए नहीं कि एक अधिक इष्टतम समाधान। यह कुछ डेटा पर तेजी से काम करता है, कुछ पर धीमा। हमें गहराई तक जाना चाहिए। यह त्रिभुज संख्याओं के साथ क्या है जो दो बार समाधान में दिखाई दिया? यह स्वीकार करने में शर्म की बात है, लेकिन मैं उच्च गणित को सुरक्षित रूप से भूल गया हूं, जहां त्रिकोण का अनुमान लगाया गया है, इसलिए मुझे इसे Google करना पड़ा।

बिंगो!

पास्कल का त्रिकोण , जैसा कि आधिकारिक तौर पर कहा जाता है। अनंत द्विपद गुणांक तालिका। तो एन अंडे और एम थ्रो के साथ समस्या का उत्तर शून्य डिग्री को छोड़कर एमटी डिग्री के न्यूटन द्विपद के विस्तार में पहले एन गुणांक का योग है।

एक मनमाना द्विपद गुणांक की गणना पंक्ति संख्या के गुणांक और पंक्ति में गुणांक संख्या के माध्यम से की जा सकती है: bk = m! / (N! * (Mn!))। लेकिन सबसे अच्छी बात यह है कि आप क्रमिक रूप से स्ट्रिंग में संख्याओं की गणना कर सकते हैं, इसकी संख्या और शून्य गुणांक (हमेशा एक): bk [n] = bk [n-1] * (m - n + 1) / n जानते हुए। प्रत्येक चरण पर, अंश एक से घटता है, और हर बढ़ता है। और संक्षिप्त अंतिम समाधान इस तरह दिखता है:

 def height(n, m): h, bk = 0, 1 #      for i in range(1, n + 1): bk = bk * m // ih += bk m-=1 return h

33 एमएस f (9477, 10000) की गणना के लिए! इस समाधान को भी अनुकूलित किया जा सकता है, हालांकि दी गई सीमाओं में और यह ठीक काम करता है। यदि n त्रिभुज की दूसरी छमाही में स्थित है, तो हम इसे mn में उल्टा कर सकते हैं, पहले n गुणांक की राशि की गणना कर सकते हैं और इसे 2 ^ m-2 से घटा सकते हैं। यदि n मध्य के करीब है और m विषम है, तो गणनाओं को भी कम किया जा सकता है: पंक्ति के पहले आधे का योग 2 ^ (m-1) -1 होगा, पहले छमाही में अंतिम गुणांक को भाज्य के माध्यम से गणना की जा सकती है, इसकी संख्या (m-1) / है 2, और फिर या तो गुणांक जोड़ना जारी रखते हैं यदि n त्रिकोण के दाहिने आधे हिस्से में है, या यदि बाईं ओर घटाना है। यदि मी सम है, तो आप पंक्ति का आधा भाग नहीं गिन सकते हैं, लेकिन आप पहले एम / 2 + 1 गुणांकों का योगफल प्राप्त कर सकते हैं, जो कि फैक्टरियल के माध्यम से औसत की गणना कर सकते हैं और इसका आधा भाग 2 ^ (एम -1) -1 में जोड़ सकते हैं। 10 ^ 6 के क्षेत्र में इनपुट डेटा पर, यह बहुत ही निष्पादन के समय को कम करता है।

एक सफल निर्णय के बाद, मैंने इस मुद्दे पर किसी और के शोध की तलाश शुरू की, लेकिन मुझे साक्षात्कार से केवल एक ही चीज मिली, केवल दो अंडे के साथ, और यह खेल नहीं है। मेरे निर्णय के बिना इंटरनेट अधूरा होगा, मैंने फैसला किया, और यहाँ यह है।

एक गगनचुंबी इमारत और अंडे के साथ एक कार्य - न्यूटन के बिन नहीं?