जूलिया। परिचित

जूलिया को ऑड

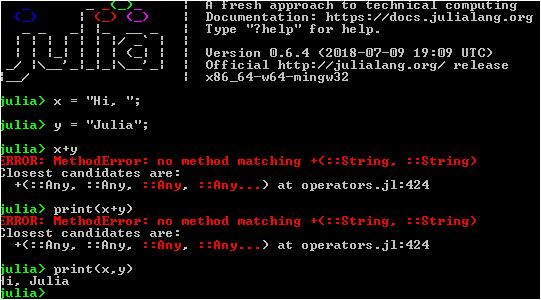
उन सभी उत्साह को व्यक्त करना बहुत मुश्किल है जो पहले कार्यक्रमों की शुरूआत और इस भाषा का उपयोग करते हुए पहली त्रुटियों के सुधार के साथ थे। पाइथन की तरह सरल और सुंदर, फोरट्रान की तरह एक सा, सरणियों और रेखांकन के साथ सुविधाजनक काम, साथ ही साथ डमी के लिए भी उग्र अनुकूलन और समानांतर प्रदर्शन करने की क्षमता मैं मेरे सहपाठियों। आप अमूर्त के विभिन्न स्तरों पर काम कर सकते हैं: गतिशील टाइपिंग के साथ उच्च-स्तरीय प्रोग्रामिंग से, आप असेंबलर कमांड पर जा सकते हैं, अर्थात्, यहां आपके पास पायथन पहुंच और फोरट्रान काउंटर के निष्पादन की गति दोनों हैं। मैं यह महसूस नहीं कर सकता कि मथकड , सिलाब और यहां तक ​​कि भगवान ने मुझे माफ कर दिया, सी ++ मेरे दिल में उतरने लगे हैं।

मैंने एक खाबरोवियन प्रकाशन पर गलती से ठोकर खाने से भाषा के बारे में सीखा, और, एक प्रभावशाली छात्र के रूप में, मुझे मार्गदर्शन की तलाश शुरू हुई, अधिमानतः रूसी में। चूंकि भाषा लगातार छह वर्षों से विकसित हो रही है, इसलिए पहले से ही सूचना के दुर्लभ स्रोत अप्रचलित हो गए, और उत्तेजना कम होने लगी। लेकिन एक प्रोग्रामिंग भाषा की मुफ्त पसंद के साथ भौतिक घटनाओं के मॉडलिंग पर एक नए प्रयोगशाला पाठ्यक्रम की शुरुआत के साथ, जूलिया के साथ परिचित शुरू करने के लिए अभी भी एक प्रेरणा थी। इसके अलावा, अगस्त में, भाषा "1.0 अप जोड़ें" ।

नीचे प्रस्तुत सामग्री को उस भाषा के परिचय के रूप में योजनाबद्ध किया गया था जिसमें सभी प्रयोगशाला पत्र लिखे गए थे और एक प्रशिक्षण पुस्तिका एकत्र की गई थी।

जूलिया गणितीय गणनाओं के लिए एक उच्च-स्तरीय, उच्च-प्रदर्शन गतिशील टाइपिंग प्रोग्रामिंग भाषा है। वाक्यविन्यास matlab परिवार के समान है, भाषा C , C ++ और योजना में लिखी गई है , Sysl पुस्तकालयों को कॉल करना संभव है

स्थापना

खैर, सब कुछ आखिरकार निपट गया, अब हमारे निपटान में है:

• JuliaPRO कमांड प्रॉम्प्ट - दुभाषिया से सीधे सभी यूलिना कौशल।
• जूनो एक सुंदर आईडीई है जिसमें ग्राफ़ के लिए एक खिड़की और एक कार्यक्षेत्र है जहां आप सभी वस्तुओं की सामग्री देख सकते हैं
• जुपिटर - कंसोल में कंप्यूटिंग कोर लॉन्च करता है, और आप सीधे ब्राउज़र में कोड निष्पादित कर सकते हैं। (जूलिया के अलावा, पायथन भी मौजूद है)

आइए देखें कि यह कैलकुलेटर क्या कर सकता है ... यूनिकोड समर्थन - आप सिरिलिक वर्णमाला, चित्रलिपि और यूनानी पत्र पी का उपयोग कर सकते हैं। और आप संख्या और चर के बीच गुणा को स्पष्ट रूप से निर्दिष्ट नहीं कर सकते हैं (उस क्रम में और बिना किसी स्थान के):

x = 5+8 2x - 3x + 2x^2 Out: 325 

सभी आवश्यक संकेत भी जगह में हैं: + =, * =, >> =, आदि। (संकेत ">>" (दाईं ओर शिफ्ट)। तुलना संकेत:>,> =, <, <= =, ==; =। असमानताओं को जंजीरों में जोड़ा जा सकता है:

 y = 5 y += 2 4 <= y < 8 Out: true 

उपलब्ध जटिल संख्या:

 (2-1im)*(4+3im) Out: 11 + 2im 

और उनके साथ काम करने के लिए कार्य:

• वास्तविक (z) वास्तविक भाग है,
• कल्पना (z) काल्पनिक हिस्सा है,
• conj (z) जटिल संयुग्म है,
• abs (z) - मॉड्यूल,
• abs2 (z) मॉड्यूल का वर्ग है,
• कोण (z) एक जटिल संख्या का तर्क है।

आप "//" और संबंधित कार्यों का उपयोग करके तर्कसंगत संख्याओं का उपयोग कर सकते हैं:

• संख्या (x) - अंश,
• डेन (x) - हर,
• फ्लोट (x) - दशमलव में कनवर्ट करता है

 x = 4//6+5//7 Out: 29//21 float(x) Out: 1.380952380952381 

जूलिया में डेटा के आंतरिक प्रतिनिधित्व को नियंत्रित करने की क्षमता है:

• typeof (obj) - वस्तु का प्रकार
• टाइपमैक्स (obj) इस प्रकार की अधिकतम संख्या है
• typemin (obj) - न्यूनतम
• eps () - मशीन शून्य
• बिगआईंट एक बड़ा संपूर्ण है
• बिगफ्लोट - बड़ा फ्लोटिंग पॉइंट

 q = 3 typemax(q) Out: 9223372036854775807 typeof(q) Out: Int64 BigFloat(2.3^45/6) Out: 3.159376405019356000000000000000000000000000000000000000000000000000000000000e+15 

कार्यों

फ़ीचर किट

• abs (x) एक संख्या का मापांक है,
• abs2 (x) मॉड्यूल का वर्ग है,
• sqrt (x) वर्गमूल है,
• cbrt (x) घनमूल है,
• exp (x) संख्या का प्रतिपादक है,
• लॉग (x) प्राकृतिक लघुगणक है,
• log10 (x) - दशमलव लघुगणक,
• log (b, x) आधार b पर x का लघुगणक है।
  साथ ही त्रिकोणमितीय, अतिपरवलयिक, हवादार, बेसेल और कई अन्य।

कस्टम कार्य:

 function () #  end 

फ़ंक्शन अंतिम अभिव्यक्ति (Mathcad उपयोगकर्ता हिचकी) का परिणाम देता है।

 function cube(x) x^3 end cube(4) Out: 64 

ठीक है, या हम स्पष्ट रूप से इंगित करते हैं:

 function myabs(x) if x>=0 return x else return -x end end myabs(-12) Out: 12 

लौटाए गए मानों को टपल में एकत्र किया जा सकता है:

 function cubeandsquare(x) x^3,x^2 end a,b = cubeandsquare(3) print("a = $a, b = $b") Out: a = 27, b = 9 

कार्य टुपल्स, डिफ़ॉल्ट मान, कीवर्ड ले सकते हैं। यदि फ़ंक्शन नाम के बाद कोई ब्रैकेट नहीं हैं, तो इसे एक चर माना जाता है और इसे दूसरे चर में सौंपा जा सकता है या पैरामीटर के रूप में फ़ंक्शन में स्थानांतरित किया जा सकता है। जूलिया कार्यक्रम लिखने की एक कार्यात्मक शैली का भी समर्थन करता है (हैलो लिस्प)

 function mysin(t;A=1,?=1,?=0) #   -     A*sin(?*t + ?) end x1 = mysin(pi) #   = 0 x2 = mysin(pi*0.5,A = 2) #      x3 = mysin(pi*0.5,? = 0.5) #      print("x1 = $x1, x2 = $x2, x3 = $x3") Out: x1 = 1.2246467991473532e-16, x2 = 2.0, x3 = 0.7071067811865475 

सरणियों

एक स्किलैब उपयोगकर्ता के रूप में, मैंने प्रतिस्थापन को नोटिस भी नहीं किया: आप फ़ंक्शन का उपयोग करके एक सरणी निर्दिष्ट कर सकते हैं:

• सरणी {T} (अपरिभाषित, dims ...) - प्रकार T की एक सरणी और आयाम dims
• शून्य (टी, dims ...) - शून्य का सरणी
• वाले (T, dims ...) - या इकाइयाँ
  $ -एंड के बजाय इंडेक्सिंग एक के साथ शुरू होती है , और मैट्रिसेस के लिए सभी आवश्यक संचालन परिभाषित किए जाते हैं (प्रदर्शन करने, कहने, तत्वपूर्ण जोड़ने या गुणा करने के लिए, आपको ऑपरेटर के सामने एक डॉट लगाने की आवश्यकता होती है)।

(अब यह स्पष्ट है कि चित्र कैसे डालें, लेकिन ठीक है ...)

मूल कार्य:

• det (A) - निर्धारक की गणना
• A ' - मैट्रिक्स को स्थानांतरित करें
• inv (A) - मैट्रिक्स को पलटना
• लंबाई (ए) - तत्वों की संख्या
• ndims (ए) - आयामों की संख्या
• size (A) - आयामों का टपल
• आकार (ए, एन) - दी गई दिशा में आयाम
• copy (A) - एरे की कॉपी बनाएं
• linspace (प्रारंभ, अंत, चरण) या
  linspace (प्रारंभ: चरण: अंत) - एक-आयामी सरणी बनाएं

 A = [1 2 3; 6 5 4; 7 8 9] Out: 3?3 Array{Int64,2}: 1 2 3 6 5 4 7 8 9 A[2,1] Out: 6 A[end] Out: 9 size(A) Out: (3, 3) 

आप ":" चिह्न के साथ आयाम के साथ सूचकांकों की एक श्रृंखला निर्दिष्ट करके सरणी के कुछ हिस्सों का चयन कर सकते हैं।

 m1 = rand(3,2) m2 = reshape(1:2:11, 3,2) Out: 3?2 Base.ReshapedArray{Int64,2,StepRange{Int64,Int64},Tuple{}}: 1 7 3 9 5 11 m3 = [m1 m2] #   (  ) Out: 3?4 Array{Float64,2}: 0.325649 0.701038 1.0 7.0 0.513579 0.620215 3.0 9.0 0.815242 0.805307 5.0 11.0 m5 = [m1; m2] #   (  ) Out: 6?2 Array{Float64,2}: 0.325649 0.701038 0.513579 0.620215 0.815242 0.805307 1.0 7.0 3.0 9.0 5.0 11.0 m3[:, 2:4] Out: 3?3 Array{Float64,2}: 0.701038 1.0 7.0 0.620215 3.0 9.0 0.805307 5.0 11.0 

यहां हमने रैंड () का उपयोग किया है, जो किसी दिए गए आयाम के यादृच्छिक संख्याओं की एक सरणी देता है, और रिशेप (), जो सरणी के आयाम को निर्दिष्ट एक में बदल देता है।

 for a in A #   a   A end 

या

 for i in eachindex(A) #     i end 

या

 for i = 1 : size(A,n) # n -      (..    ) #     i end 

ग्राफिक्स

ग्राफिक्स का उपयोग करने के लिए, आपको चुनने के लिए रिपॉजिटरी से एक पैकेज डाउनलोड करना होगा:

• Pkg.add ("प्लॉट्स")
• Pkg.add ("PyPlot")
• Pkg.add ("Gadfly")
• Pkg.add ("विंस्टन")

इनमें से, सबसे लोकप्रिय Pythonic PyPlot है । उदाहरण के लिए, मॉड्यूल कमांड का उपयोग करके जुड़े हुए हैं:

 using PyPlot 

हालाँकि, आइए गैस्ट्रॉन को ग्नुप्लोट (अलग से स्विंग) का उपयोग करके देखें।
Gaston.jl टीम द्वारा लोड किया गया

  Pkg.add("Gaston") 

और बिंदु पर अधिकार:

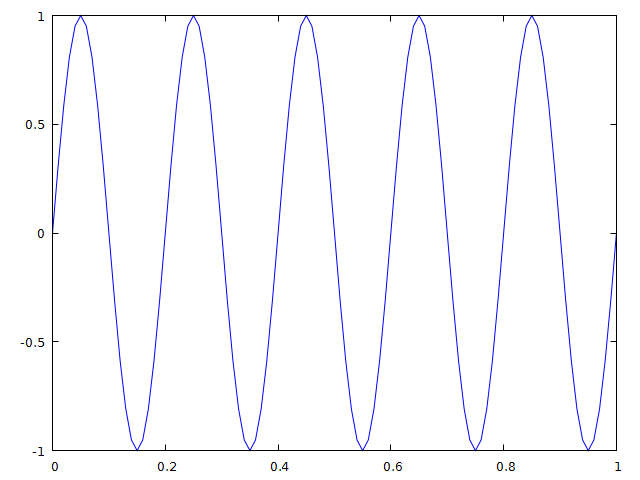
 using Gaston t = 0:0.01:1 plot(t, sin.(2?*5*t)) 

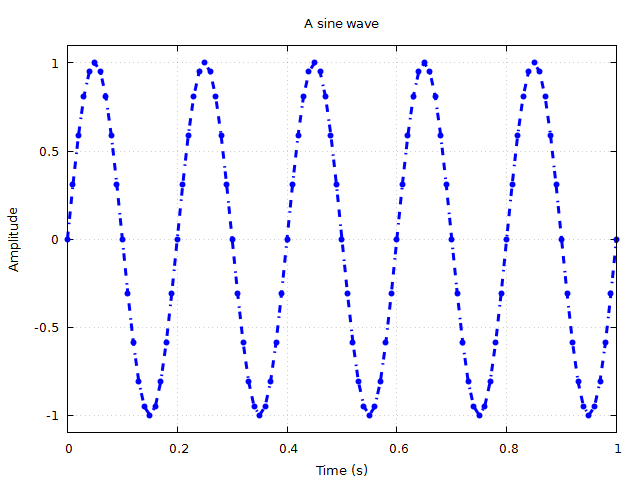
 plot(t,sin.(2?*5*t),title="A sine wave",xlabel="Time (s)",ylabel="Amplitude",grid="on",linewidth=3,color="blue", yrange="[-1.1:1.1]",marker="ecircle",plotstyle="linespoints",linestyle="-.-") 

 plot!(t,cos.(2?*5*t),color="red",linewidth=2) #       

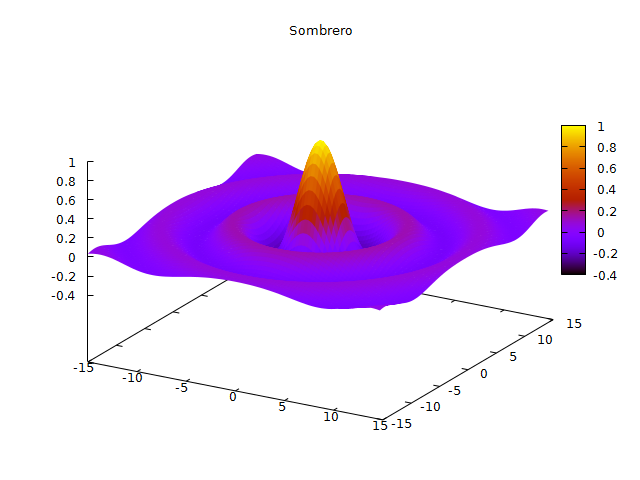
 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt.(x.*x+y.*y))./sqrt.(x.*x+y.*y),title="Sombrero",plotstyle="pm3d") 

 x = y = -15:0.33:15 surf(x,y,(x,y)->sin.(sqrt(x.*x+y.*y))./sqrt.(x.*x+y.*y), title="Edge view of a sombrero",plotstyle="pm3d",gpcom="set view 80,20") 

 R = [ x+y for x=0:5:120, y=0:5:120] G = [ x+y for x=0:5:120, y=120:-5:0] B = [ x+y for x=120:-5:0, y=0:5:120] Z = zeros(25,25,3) Z[:,:,1] = R Z[:,:,2] = G Z[:,:,3] = B imagesc(Z,title="RGB Image",clim=[10 200]) 

 histogram(rand(1000),bins=15,norm=1,title="Histogram",yrange="[0:1.6]") 

 y = 1:40 err = Gaston.ErrorCoords(rand(40)) plot(y,err=err,title="Example of error bars",plotstyle="errorbars") 

आप एच = फिगर () कमांड (सिर्फ प्लॉट्स के बीच इंसर्ट) का उपयोग करके कई ग्राफिकल विंडो ( ज्यूपिटर में काम नहीं करता है) बना सकते हैं। ग्राफ़ को एक छवि फ़ाइल के रूप में सहेजने के लिए, कमांड का उपयोग करें
set_filename ("name.png") # निर्दिष्ट नहीं होने पर प्रदर्शित किया जाएगा
Printfigure ("पीएनजी") # फाइल को बचाने के लिए, पीएनजी, पीडीएफ, एसवीजी और जीआईएफ उपलब्ध
अधिक गैस्टन पैकेज की जानकारी

निष्कर्ष

हर स्वाद और लगभग सभी जरूरतों को कवर करने के लिए कई और ग्राफिक पैकेज हैं। इसके अलावा, सहायक पैकेज संभवतः और मुख्य के साथ विकसित हो रहे हैं। यहां आपके पास क्वांटम कंप्यूटिंग, और जैव सूचना विज्ञान, और मशीन सीखने और डिफ्यूज़र और डेरिवेटिव जैसी कई और अधिक दबाव वाली समस्याएं हैं।

सामान्य तौर पर, जूलिया सुंदर, होशियार और बहुत ही होनहार है, और बिना ध्यान दिए उसे छोड़ना बेहद असाध्य है।