समान रूप से पाइटोर और टेंसरफ्लो में क्षेत्र भर में अंक वितरित करते हैं

यह पाठ उन लोगों के लिए लिखा गया है जो गहरी शिक्षा में रुचि रखते हैं, जो कई चर के कार्य को कम करने के लिए पाइटोरेक और टेंसोफ़्लो लाइब्रेरी के विभिन्न तरीकों का उपयोग करना चाहते हैं, जो सीखने में रुचि रखते हैं कि कैसे वेक्टर के रूप में निष्पादित मैट्रिक्स गणना में क्रमिक रूप से निष्पादित प्रोग्राम को चालू किया जाए। आप यह भी सीख सकते हैं कि पोवेरे और वापोरी का उपयोग करके देखे गए डेटा से कार्टून कैसे बनाया जाए।

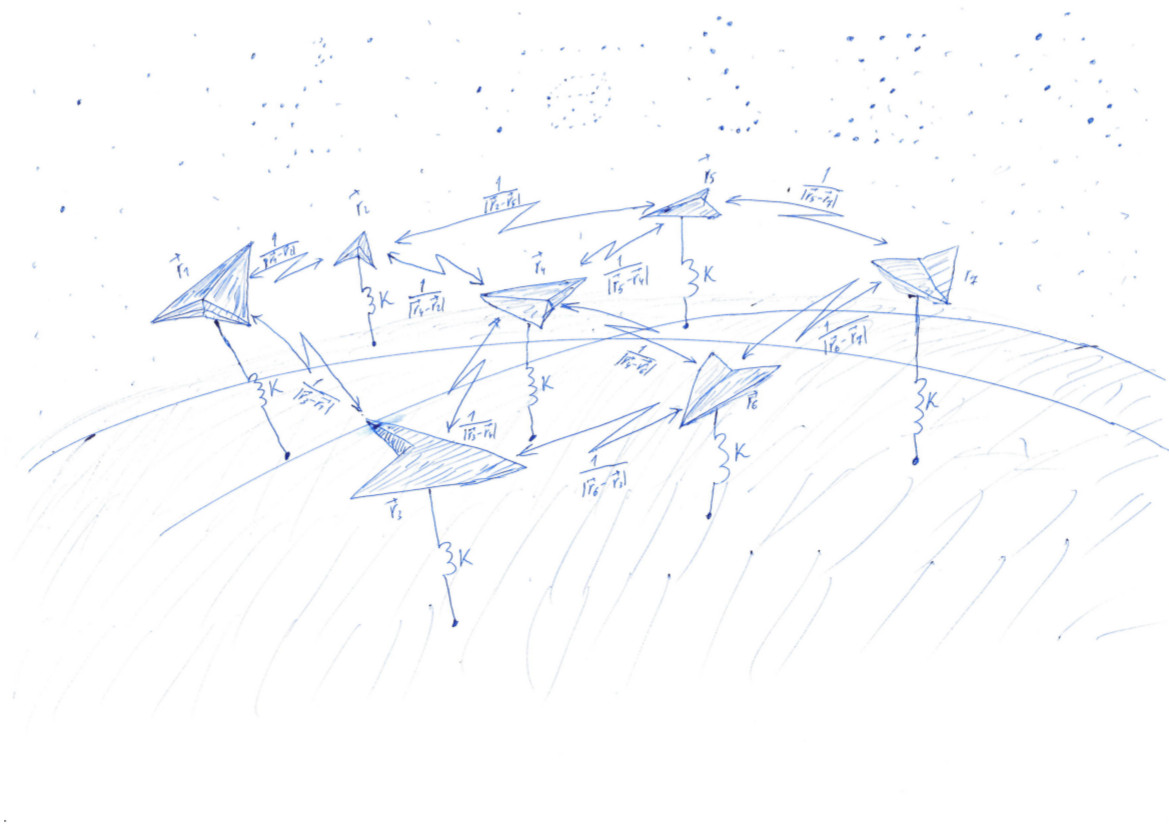
कार्य कहां से है

प्रत्येक अपनी कार्यक्षमता को कम करता है (सी) बेनामी डेटा वैज्ञानिक

हमारे ब्लॉग के पिछले प्रकाशनों में से एक में, "रेक नंबर 6" पैराग्राफ में, हमने DSSM तकनीक के बारे में बात की, जो आपको पाठ को वैक्टर में बदलने की अनुमति देता है। इस तरह के मानचित्रण को खोजने के लिए, रैखिक परिवर्तनों के गुणांकों को खोजने की आवश्यकता होती है, जो कि जटिल जटिल नुकसान को कम करते हैं। इस तरह के मॉडल को सीखना क्या होता है, इसे समझना वैक्टर की बड़ी आयामीता के कारण मुश्किल है। एक अंतर्ज्ञान विकसित करने के लिए जो आपको अनुकूलन विधि चुनने और इस पद्धति के मापदंडों को निर्धारित करने की अनुमति देता है, आप इस कार्य के सरलीकृत संस्करण पर विचार कर सकते हैं। अब वैक्टर हमारे सामान्य त्रि-आयामी अंतरिक्ष में हैं, फिर उन्हें खींचना आसान है। और नुकसान फ़ंक्शन को अलग-अलग बिंदुओं को धक्का देने और इकाई क्षेत्र के लिए आकर्षण की क्षमता होगी। इस मामले में, समस्या का समाधान क्षेत्र पर बिंदुओं का एक समान वितरण होगा। वर्तमान समाधान की गुणवत्ता को आंख से मूल्यांकन करना आसान है।

इसलिए, हम किसी दिए गए परिमाण में एक समान वितरण की तलाश करेंगे $$$एन$ अंक। इस तरह के वितरण को कभी-कभी ध्वनिकी के लिए आवश्यक होता है ताकि यह समझ सके कि किस दिशा में एक क्रिस्टल में एक लहर लॉन्च करना है। सिग्नलमैन - यह पता लगाने के लिए कि सर्वोत्तम गुणवत्ता संचार प्राप्त करने के लिए उपग्रहों को कक्षा में कैसे रखा जाए। मौसम विज्ञानी - मौसम निगरानी स्टेशनों की नियुक्ति के लिए।

कुछ के लिए $$$एन$ कार्य आसानी से हल हो गया है । उदाहरण के लिए, यदि $$$n = 8$ , हम घन ले सकते हैं और इसके कोने समस्या का जवाब देंगे। हम भाग्यशाली भी हैं अगर $$$एन$ icosahedron, dodecahedron, या अन्य प्लेटोनिक ठोस के कोने की संख्या के बराबर होगा। अन्यथा, कार्य इतना सरल नहीं है।

पर्याप्त रूप से बड़ी संख्या में अंकों के लिए, अनुभवजन्य रूप से चयनित गुणांकों के साथ एक सूत्र है , कई और विकल्प यहां , यहां , और यहां हैं । लेकिन एक और अधिक सार्वभौमिक है, यद्यपि अधिक जटिल, समाधान जिसके लिए यह लेख समर्पित है।

हम थॉमसन समस्या ( विकी ) के समान एक समस्या का समाधान करते हैं। बिखराव $$$एन$ अंक बेतरतीब ढंग से, और फिर उन्हें एक सतह पर आकर्षित करते हैं, जैसे कि एक गोले के रूप में, और एक दूसरे से दूर धक्का। आकर्षण और प्रतिकर्षण कार्य - क्षमता द्वारा निर्धारित होते हैं। संभावित फ़ंक्शन के न्यूनतम मूल्य पर, अंक क्षेत्र पर समान रूप से समान रूप से स्थित होंगे।

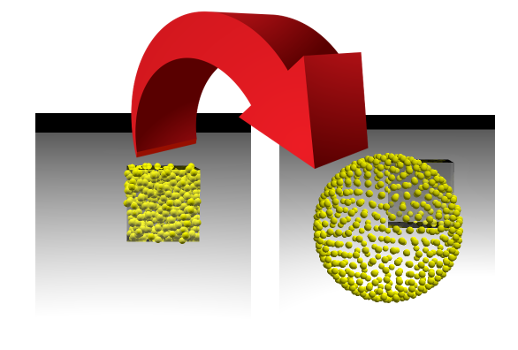
यह कार्य मशीन लर्निंग (एमएल) मॉडल की सीखने की प्रक्रिया से काफी मिलता-जुलता है, जिसके दौरान हानि फ़ंक्शन को कम से कम किया जाता है। लेकिन एक डेटा वैज्ञानिक आमतौर पर देखता है कि एक एकल संख्या कैसे घटती है, और हम तस्वीर को बदल सकते हैं। अगर हम सफल होते हैं, तो हम देखेंगे कि किस तरह से क्यूब के अंदर बेतरतीब ढंग से साइड 1 के साथ बिंदुओं को गोलाकार की सतह के साथ रखा जाता है:

योजना के अनुसार, समस्या को हल करने के लिए एल्गोरिथ्म का प्रतिनिधित्व निम्न प्रकार से किया जा सकता है। तीन-आयामी अंतरिक्ष में स्थित प्रत्येक बिंदु मैट्रिक्स की एक पंक्ति से मेल खाती है $$$X$ । इस मैट्रिक्स से हानि फ़ंक्शन की गणना की जाती है। $$$एल$ का न्यूनतम मूल्य, गोले के ऊपर बिंदुओं के एक समान वितरण से मेल खाता है। pytorch और tensorflow का उपयोग करके न्यूनतम मूल्य पाया जाता है, जो मैट्रिक्स द्वारा नुकसान फ़ंक्शन के ग्रेडिएंट की गणना करने की अनुमति देता है $$$X$ और लाइब्रेरी में लागू किए गए तरीकों में से एक का उपयोग करके न्यूनतम पर जाएं: SGD, ADAM, ADAGRAD, आदि।

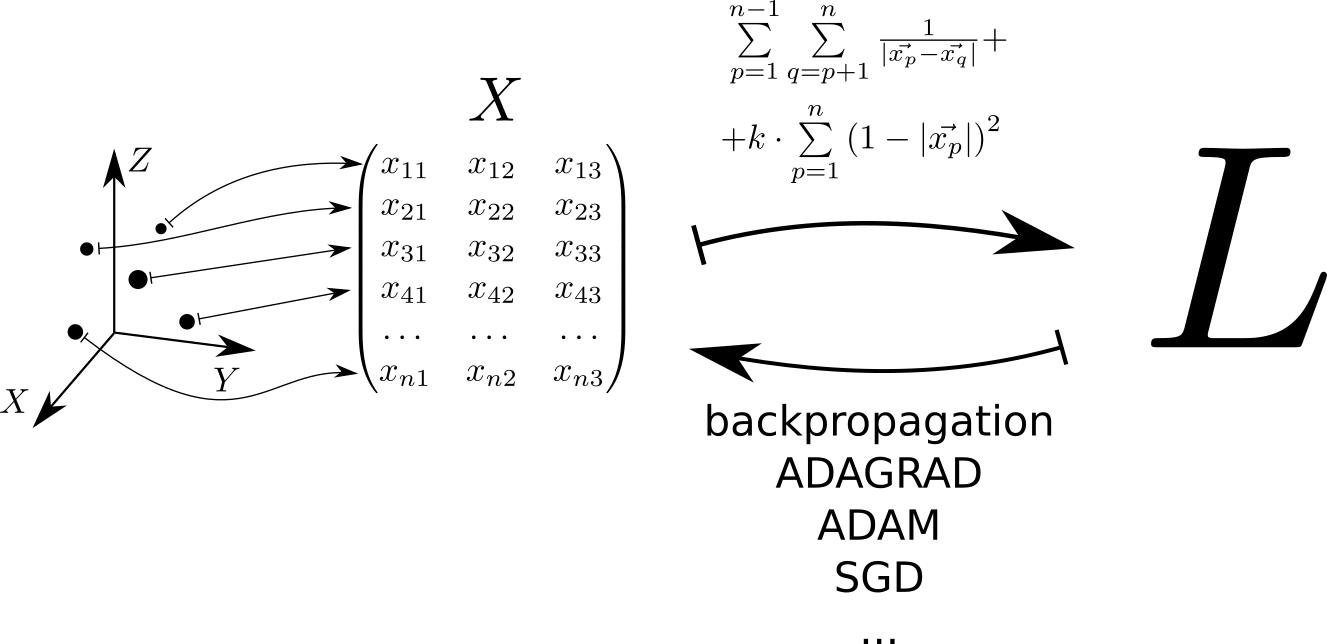
हम क्षमता पर विचार करते हैं

इसकी सादगी, अभिव्यक्ति और अन्य भाषाओं में लिखी गई पुस्तकालयों के लिए एक इंटरफ़ेस के रूप में सेवा करने की क्षमता के कारण, पायथन का उपयोग मशीन सीखने की समस्याओं को हल करने के लिए व्यापक रूप से किया जाता है। इसलिए, इस लेख में कोड उदाहरण पायथन में लिखे गए हैं। तेजी से मैट्रिक्स की गणना के लिए, हम संख्यात्मक पुस्तकालय का उपयोग करेंगे। कई वैरिएबल्स के कार्य को कम करने के लिए - पाइरॉच और टेंसोफ़्लो।

हम 1 के साथ घन में बेतरतीब ढंग से तितर बितर अंक। हमें 500 अंक है, और इलेक्ट्रोस्टैटिक की तुलना में लोचदार बातचीत 1000 गुना अधिक महत्वपूर्ण है:

 import numpy as np n = 500 k = 1000 X = np.random.rand(n, 3) 

इस कोड ने एक मैट्रिक्स उत्पन्न किया $$$X$ आकार $$$3 \ n n$ 0 से 1 तक यादृच्छिक संख्याओं से भरा:

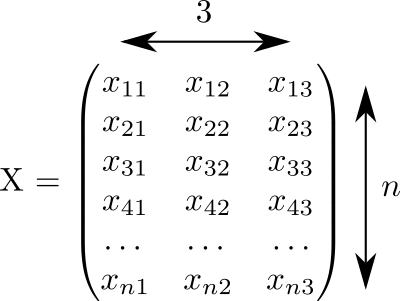
हम मानते हैं कि इस मैट्रिक्स की प्रत्येक पंक्ति एक बिंदु से मेल खाती है। और तीन कॉलम में निर्देशांक दर्ज किए जाते हैं $$$x, y, z$ हमारे सभी बिंदु।

एक इकाई की सतह के साथ एक बिंदु के लोचदार संपर्क की क्षमता $$$u_1 = k \ cdot (1 - r) ^ 2/2$ । बिंदुओं के इलेक्ट्रोस्टैटिक इंटरैक्शन की क्षमता $$$पी$ और $$$q$ - $$$u_2 = 1 / | r_p - r_q |$ । पूरी क्षमता में सभी बिंदुओं के इलेक्ट्रोस्टैटिक इंटरैक्शन और प्रत्येक बिंदु के लोचदार संपर्क क्षेत्र के सतह के साथ होते हैं:

$$

$$U (x_1, ..., x_n) = \ योग \ सीमाएं _ {p = 1} ^ {n - 1} \ योग \ सीमाएं _ {q = p + 1} ^ {n} \ frac 1 {\ बाईं ओर | \ vec {x_p} - \ vec {x_q} \ right | } + k \ cdot \ योग \ सीमाएँ _ {p = 1} ^ n \ left (1 - | \ vec {__p} | \ right) ^ 2 \ rightarrow \ min$$

सिद्धांत रूप में, इस सूत्र का उपयोग करके संभावित मूल्य की गणना की जा सकती है:

 L_for = 0 L_for_inv = 0 L_for_sq = 0 for p in range(n): p_distance = 0 for i in range(3): p_distance += x[p, i]**2 p_distance = math.sqrt(p_distance) L_for_sq += k * (1 - p_distance)**2 #     ,     for q in range(p + 1, n): if q != p: pq_distance = 0 for i in range(3): pq_distance += (x[p, i] - x[q, i]) ** 2 pq_distance = math.sqrt(pq_distance) L_for_inv += 1 / pq_distance #      L_for = (L_for_inv + L_for_sq) / n print('loss =', L_for) 

लेकिन थोड़ी परेशानी है। एक दयनीय 2000 अंक के लिए, यह कार्यक्रम 2 सेकंड के लिए चलेगा। यदि हम इस मूल्य की गणना वेक्टरकृत मैट्रिक्स गणनाओं का उपयोग करके करेंगे तो यह बहुत तेज़ होगा। त्वरण मैट्रिक्स के कार्यान्वयन के माध्यम से दोनों "फास्ट" भाषाओं फोरट्रान और सी का उपयोग करके प्राप्त किया जाता है, और वेक्टर प्रोसेसर के उपयोग के माध्यम से जो एक घड़ी चक्र में बड़ी मात्रा में इनपुट डेटा पर कार्रवाई करने की अनुमति देता है।

आइए मैट्रिक्स देखें $$$S = X \ cdot X ^ T$ । इसमें कई दिलचस्प गुण हैं और अक्सर यह एमएल में रैखिक क्लासफायर के सिद्धांत से संबंधित गणनाओं में पाया जाता है। तो, अगर हम मान लें कि मैट्रिक्स की पंक्ति में $$$X$ सूचकांकों के साथ $$$पी$ और $$$q$ तीन आयामी अंतरिक्ष वैक्टर लिखे जाते हैं $$$\ vec {r_ p}, \ vec {r_q}$ फिर मैट्रिक्स $$$एस$ इन वैक्टर के अदिश उत्पादों से मिलकर बनेगा। ऐसे वैक्टर $$$एन$ टुकड़े, फिर मैट्रिक्स का आयाम $$$एस$ के बराबर है $$$n \ n n$ ।

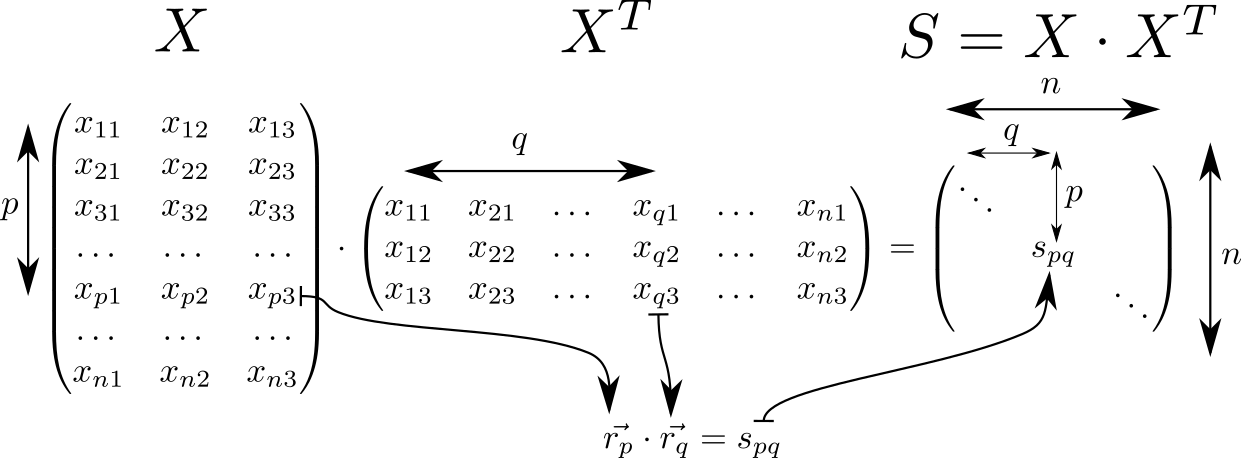
मैट्रिक्स के विकर्ण पर $$$एस$ वैक्टर की लंबाई के वर्ग खड़े हो जाओ $$$\ vec {r_p}: s_ {p p} = r_p ^ 2$ । यह जानते हुए, चलो बातचीत की पूरी क्षमता पर विचार करें। हम दो सहायक मैट्रिक्स की गणना करके शुरू करते हैं। एक विकर्ण मैट्रिक्स में $$$एस$ पंक्तियों में दोहराया जाएगा, दूसरे में - कॉलम में।

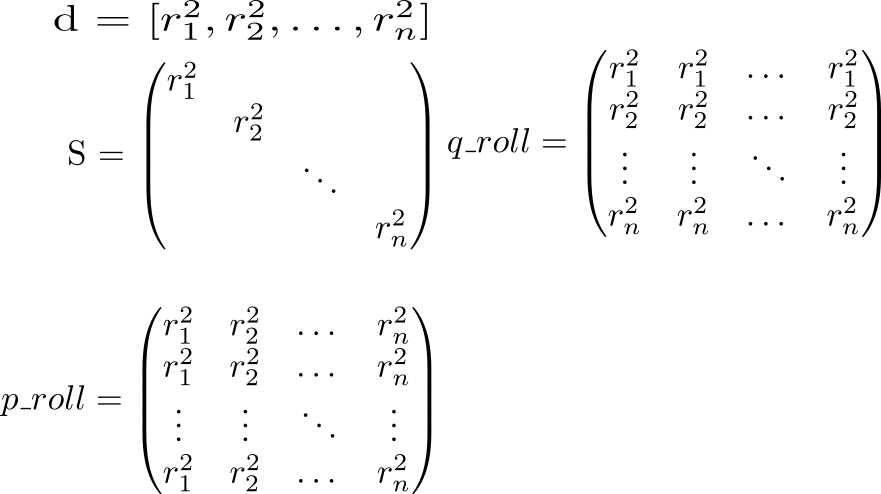
अब आइए अभिव्यक्ति p_roll + q_roll - 2 * S

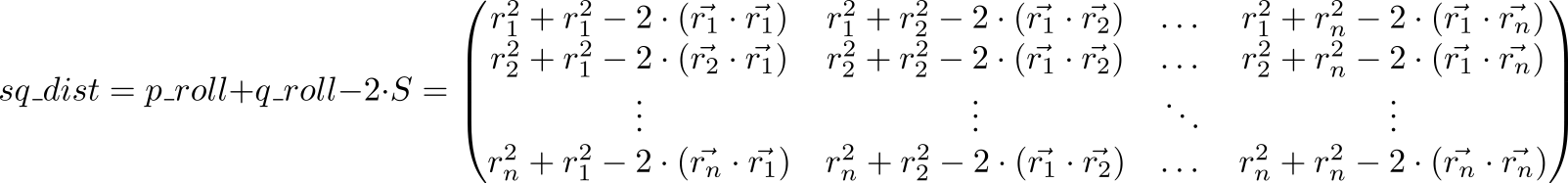
अनुक्रमित वस्तु $$$(p, q)$ मैट्रिक्स sq_dist बराबर है $$$r_p ^ 2 + r_q ^ 2 - 2 \ cdot (\ vec {r_p}, \ vec {r_q}) = ((vec {r_p} - \ vec {r_q}) - 2$ । यही है, हमारे पास बिंदुओं के बीच दूरियों के वर्गों का एक मैट्रिक्स है।

एक क्षेत्र पर इलेक्ट्रोस्टैटिक प्रतिकर्षण

dist = np.sqrt(sq_dist) - बिंदुओं के बीच की दूरी का मैट्रिक्स। हमें अपने और आकर्षण के बीच के बिंदुओं के प्रतिकर्षण को ध्यान में रखते हुए, क्षमता की गणना करने की आवश्यकता है। इकाइयों को विकर्ण पर रखें और प्रत्येक तत्व को इसके व्युत्क्रम से बदलें (बस यह मत सोचो कि हम मैट्रिक्स को rec_dist_one = 1 / (dist + np.eye(n)) !): rec_dist_one = 1 / (dist + np.eye(n)) । परिणाम विकर्ण पर एक मैट्रिक्स है जिसमें इकाइयां हैं, अन्य तत्व बिंदुओं के बीच इलेक्ट्रोस्टैटिक इंटरैक्शन की क्षमता हैं।

अब हम इकाई क्षेत्र की सतह पर आकर्षण की द्विघातीय क्षमता को जोड़ते हैं। गोले की सतह से दूरी $$$(1 - r)$ । इसे स्क्वायर करें और इसके द्वारा गुणा करें $$$k$ , जो कणों के इलेक्ट्रोस्टैटिक प्रतिकर्षण की भूमिका और एक क्षेत्र के आकर्षण के बीच संबंध को परिभाषित करता है। कुल k = 1000 , all_interactions = rec_dist_one - torch.eye(n) + (d.sqrt() - torch.ones(n))**2 । लंबे समय से प्रतीक्षित हानि फ़ंक्शन, जिसे हम न्यूनतम करेंगे: t = all_interactions.sum()

एक प्रोग्राम जो संभावित लाइब्रेरी का उपयोग करके गणना करता है:

 S = X.dot(XT) #    pp_sq_dist = np.diag(S) #  p_roll = pp_sq_dist.reshape(1, -1).repeat(n, axis=0) #     q_roll = pp_sq_dist.reshape(-1, 1).repeat(n, axis=1) #     pq_sq_dist = p_roll + q_roll - 2 * S #      pq_dist = np.sqrt(pq_sq_dist) #    pp_dist = np.sqrt(pp_sq_dist) #      surface_dist_sq = (pp_dist - np.ones(n)) ** 2 #       rec_pq_dist = 1 / (pq_dist + np.eye(n)) - np.eye(n) #      L_np_rec = rec_pq_dist.sum() / 2 #     L_np_surf = k * surface_dist_sq.sum() #       L_np = (L_np_rec + L_np_surf) / n #   ,     print('loss =', L_np) 

यहां 2000 से 200 अंकों में चीजें थोड़ी बेहतर हैं।

हम pytorch का उपयोग करते हैं:

 import torch pt_x = torch.from_numpy(X) # pt_x -   tensor   pytorch pt_S = pt_x.mm(pt_x.transpose(0, 1)) # mm - matrix multiplication pt_pp_sq_dist = pt_S.diag() pt_p_roll = pt_pp_sq_dist.repeat(n, 1) pt_q_roll = pt_pp_sq_dist.reshape(-1, 1).repeat(1, n) pt_pq_sq_dist = pt_p_roll + pt_q_roll - 2 * pt_S pt_pq_dist = pt_pq_sq_dist.sqrt() pt_pp_dist = pt_pp_sq_dist.sqrt() pt_surface_dist_sq = (pt_pp_dist - torch.ones(n, dtype=torch.float64)) ** 2 pt_rec_pq_dist = 1/ (pt_pq_dist + torch.eye(n, dtype=torch.float64)) - torch.eye(n, dtype=torch.float64) L_pt = (pt_rec_pq_dist.sum() / 2 + k * pt_surface_dist_sq.sum()) / n print('loss =', float(L_pt)) 

और अंत में टेंसरफ़्लो:

 import tensorflow as tf tf_x = tf.placeholder(name='x', dtype=tf.float64) tf_S = tf.matmul(tf_x, tf.transpose(tf_x)) tf_pp_sq_dist = tf.diag_part(tf_S) tf_p_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (1, -1)), (n, 1)) tf_q_roll = tf.tile(tf.reshape(tf_pp_sq_dist, (-1, 1)), (1, n)) tf_pq_sq_dist = tf_p_roll + tf_q_roll - 2 * tf_S tf_pq_dist = tf.sqrt(tf_pq_sq_dist) tf_pp_dist = tf.sqrt(tf_pp_sq_dist) tf_surface_dist_sq = (tf_pp_dist - tf.ones(n, dtype=tf.float64)) ** 2 tf_rec_pq_dist = 1 / (tf_pq_dist + tf.eye(n, dtype=tf.float64)) - tf.eye(n, dtype=tf.float64) L_tf = (tf.reduce_sum(tf_rec_pq_dist) / 2 + k * tf.reduce_sum(tf_surface_dist_sq)) / n glob_init = tf.local_variables_initializer() #     with tf.Session() as tf_s: #     glob_init.run() #   res, = tf_s.run([L_tf], feed_dict={tf_x: x}) #   print(res) 

इन तीन तरीकों के प्रदर्शन की तुलना करें:

एन	अजगर	numpy	pytorch	tensorflow
2000	4.03	0.083	1.11	0.205
10000	99	2.82	2.18	7.9

वेक्टर की गई गणना शुद्ध अजगर कोड के सापेक्ष डेढ़ दशमलव से अधिक ऑर्डर का लाभ देती है। पाइरॉच में "बॉयलर प्लेट" दिखाई देती है: छोटी मात्रा की गणना में ध्यान देने योग्य समय लगता है, लेकिन गणना की बढ़ती मात्रा के साथ यह लगभग नहीं बदलता है।

दृश्य

आजकल, डेटा को भारी संख्या में पैकेजों का उपयोग करके देखा जा सकता है, जैसे कि मैटलैब, वोल्फ्राम मैथेमेटिका, मेपल, मेटप्लोटलिब, आदि। इन पैकेजों में बहुत सारे जटिल कार्य होते हैं जो जटिल चीजें करते हैं। दुर्भाग्य से, यदि आप एक सरल लेकिन गैर-मानक कार्य का सामना करते हैं, तो आप खुद को निहत्था पाते हैं। इस स्थिति में मेरा पसंदीदा समाधान पोवरे है। यह एक बहुत ही शक्तिशाली कार्यक्रम है जिसका उपयोग आमतौर पर फोटोरिअलिस्टिक इमेज बनाने के लिए किया जाता है, लेकिन इसका उपयोग "विज़ुअलाइज़ेशन ऑफ़ विज़ुअलाइज़ेशन" के रूप में किया जा सकता है। आमतौर पर, कोई फर्क नहीं पड़ता कि आप कितनी सतह को प्रदर्शित करना चाहते हैं, बस पोवेरे को उस सतह पर स्थित केंद्रों के साथ गोले खींचने के लिए कहें।

वैपोरी लाइब्रेरी का उपयोग करके, आप सीधे अजगर में एक पॉवरे दृश्य बना सकते हैं, इसे प्रस्तुत कर सकते हैं और परिणाम देख सकते हैं। अब यह इस तरह दिखता है:

चित्र निम्नानुसार प्राप्त किया जाता है:

 import vapory from PIL import Image def create_scene(moment): angle = 2 * math.pi * moment / 360 r_camera = 7 camera = vapory.Camera('location', [r_camera * math.cos(angle), 1.5, r_camera * math.sin(angle)], 'look_at', [0, 0, 0], 'angle', 30) light1 = vapory.LightSource([2, 4, -3], 'color', [1, 1, 1]) light2 = vapory.LightSource([2, 4, 3], 'color', [1, 1, 1]) plane = vapory.Plane([0, 1, 0], -1, vapory.Pigment('color', [1, 1, 1])) box = vapory.Box([0, 0, 0], [1, 1, 1], vapory.Pigment('Col_Glass_Clear'), vapory.Finish('F_Glass9'), vapory.Interior('I_Glass1')) spheres = [vapory.Sphere( [float(r[0]), float(r[1]), float(r[2])], 0.05, vapory.Texture(vapory.Pigment('color', [1, 1, 0]))) for r in x] return vapory.Scene(camera, objects=[light1, light2, plane, box] + spheres, included=['glass.inc']) for t in range(0, 360): flnm = 'out/sphere_{:03}.png'.format(t) scene = create_scene(t) scene.render(flnm, width=800, height=600, remove_temp=False) clear_output() display(Image.open(flnm)) 

फ़ाइलों के एक समूह से, एनिमेटेड GIF को ImageMagic का उपयोग करके इकट्ठा किया जाता है:

 convert -delay 10 -loop 0 sphere_*.png sphere_all.gif 

गितुब पर आप कार्य कोड देख सकते हैं, जिसके टुकड़े यहाँ दिए गए हैं। दूसरे लेख में, मैं इस बारे में बात करूंगा कि कार्यात्मक को कम करने की शुरुआत कैसे करें ताकि अंक घन से बाहर आएं और समान रूप से पूरे क्षेत्र में फैल जाएं।