प्रतीकात्मक गणनाओं द्वारा गणितीय वस्तुओं की गणितीय समस्याओं को हल करने के लिए प्रतीकात्मक गणनाओं का उपयोग करके एल्गोरिदम का कार्यान्वयन बहुत सुविधाजनक है। इस तरह के समीकरणों को हल करने के लिए, लाप्लास रूपांतरों का व्यापक रूप से उपयोग किया जाता है, जो सरल शब्दों में, सरल बीजगणितीय समीकरणों को हल करने के लिए समस्या को कम करना संभव बनाता है।
इस प्रकाशन में, मैं सिम्पी लाइब्रेरी से प्रत्यक्ष और व्युत्क्रम लाप्लास परिवर्तनों के कार्यों पर विचार करने का प्रस्ताव करता हूं, जो आपको पायथन का उपयोग करके अंतर समीकरणों और प्रणालियों को हल करने के लिए लाप्लास विधि का उपयोग करने की अनुमति देता है।
लाप्लास विधि ही और रैखिक अंतर समीकरणों और प्रणालियों को हल करने में इसके फायदे साहित्य में व्यापक रूप से शामिल हैं, उदाहरण के लिए, लोकप्रिय प्रकाशन [1] में। पुस्तक में, लाप्लास विधि लेखक द्वारा चयनित उदाहरणों का उपयोग करके लाइसेंस प्राप्त सॉफ्टवेयर पैकेज मैथेमेटिका, मेपल और MATLAB (जो एक शैक्षिक संस्थान द्वारा इस सॉफ्टवेयर की खरीद का तात्पर्य है) में कार्यान्वयन के लिए प्रस्तुत की गई है।
आज हम पायथन का उपयोग करके सीखने की समस्या को हल करने के एक अलग उदाहरण पर विचार नहीं करने की कोशिश करेंगे, लेकिन प्रत्यक्ष और व्युत्क्रम लाप्लास परिवर्तनों के उपयोग से रैखिक अंतर समीकरणों और प्रणालियों को हल करने के लिए एक सामान्य विधि। उसी समय, हम एक सीखने के क्षण को बचाएंगे: काऊची स्थितियों के साथ रैखिक अंतर समीकरण के बाईं ओर का निर्माण छात्र स्वयं करेगा, और कार्य का नियमित हिस्सा, समीकरण के दाईं ओर के प्रत्यक्ष लाप्लास परिवर्तन में शामिल होगा,
laplace_transform () फ़ंक्शन का उपयोग करके प्रदर्शन किया जाएगा।
लाप्लास के लेखक की कहानी बदल देती है
लाप्लास रूपांतर (लाप्लास चित्र) का एक दिलचस्प इतिहास है। पहली बार, लैप्लस रूपांतरण की परिभाषा में एल। यूलर के कार्यों में से एक में अभिन्न अंग दिखाई दिया। हालाँकि, यह आम तौर पर गणित में स्वीकार किया जाता है कि एक पद्धति या प्रमेय को गणितज्ञ का नाम कहा जाता है जिसने इसे यूलर के बाद खोजा था। अन्यथा, कई सौ अलग-अलग यूलर प्रमेय होंगे।
इस मामले में, यूलर के बाद अगला फ्रांसीसी गणितज्ञ पियरे साइमन डी लाप्लास (पियरे साइमन डी लाप्लास (1749-1827)) था। यह वह था जिसने संभावना सिद्धांत पर अपने काम में इस तरह के अभिन्न का इस्तेमाल किया। लाप्लास रूपांतरों (लाप्लास छवियों) के आधार पर अंतर समीकरणों के समाधान खोजने के लिए लाप्लास ने स्वयं तथाकथित "परिचालन विधियों" को लागू नहीं किया। इन तरीकों को वास्तव में व्यावहारिक इंजीनियरों द्वारा खोजा गया और लोकप्रिय बनाया गया, खासकर अंग्रेजी इलेक्ट्रिकल इंजीनियर ओलिवर हीविसाइड (1850-1925)। लंबे समय से पहले इन तरीकों की वैधता को सख्ती से साबित किया गया था, परिचालन पथरी सफलतापूर्वक और व्यापक रूप से उपयोग किया गया था, हालांकि 20 वीं शताब्दी की शुरुआत में भी इसकी वैधता पर काफी हद तक सवाल उठाया गया था, और इस विषय पर बहुत ही भयंकर बहस हुई थी।
प्रत्यक्ष और व्युत्क्रम लाप्लास के कार्य रूपांतरित होते हैं
- लाप्लास प्रत्यक्ष परिवर्तन
sympy.integrals.transforms। laplace_transform (टी, एस, ** संकेत)।
Laplace_transform () फ़ंक्शन वास्तविक चर के फ़ंक्शन f (t) के लाप्लास रूपांतरणों को जटिल चर के फ़ंक्शन F (s) में करता है, ताकि:
एफ ( रों ) = मैं एन टी एफ 0 च ( टी ) ई - रों टी डी टी $
यह फ़ंक्शन रिटर्न (एफ, ए, कंडस) , जहां एफ (एस) फ़ंक्शन एफ (टी) का लाप्लास रूपांतरण है, ए <रे (एस) आधा विमान है जहां एफ (एस) को परिभाषित किया गया है, और कोंड अभिन्न के अभिसरण के लिए सहायक स्थितियां हैं।
यदि इंटीग्रल को बंद रूप में गणना नहीं की जा सकती है, तो यह फ़ंक्शन एक असंपीड़ित लैपलैसट्रांसफॉर्म ऑब्जेक्ट लौटाता है।
यदि आप विकल्प noconds = true सेट करते हैं, तो फ़ंक्शन केवल F (s) देता है । - उलटा लाप्लास परिवर्तन समारोह:
sympy.integrals.transforms। inverse_laplace_transform (एफ, एस, टी, विमान = कोई नहीं, ** संकेत)।
व्युत्क्रम_ laplace_transform () फ़ंक्शन उल्टे लाप्लास को वास्तविक चर के फ़ंक्शन f (t) में जटिल चर F (s) के कार्य का रूपांतरण करता है, ताकि:
f(t)= frac12 pii intc+∞ cdotic−∞ cdotiestF(s)ds$
यदि इंटीग्रल की गणना बंद रूप में नहीं की जा सकती है, तो यह फ़ंक्शन ऑब्जेक्ट के अनलॉस्ड InverseLaplaceTransform को लौटाता है।
उलटा लाप्लास नियामकों की संक्रमण विशेषताओं को निर्धारित करने के उदाहरण पर बदल जाता है
PID कंट्रोलर के ट्रांसफर फंक्शन का फॉर्म है [2]:
W(s)=(1+ fracKd cdotTd cdots1+Td cdots) CdotKp cdot(1+ )frac1Ti cdots) c d o t f r a c 1 s $
हम कम स्थानांतरण फ़ंक्शन के लिए पीआईडी और पीआई नियंत्रकों की क्षणिक विशेषताओं के लिए समीकरण प्राप्त करने के लिए एक कार्यक्रम लिखेंगे, और इसके अलावा उलटा दृश्य लाप्लास परिवर्तन पर खर्च किए गए समय को प्राप्त करेंगे।
हमें मिलता है:रिवर्स लाइपलेस ट्रांसफॉर्मेशन टाइम: 2.68 एस
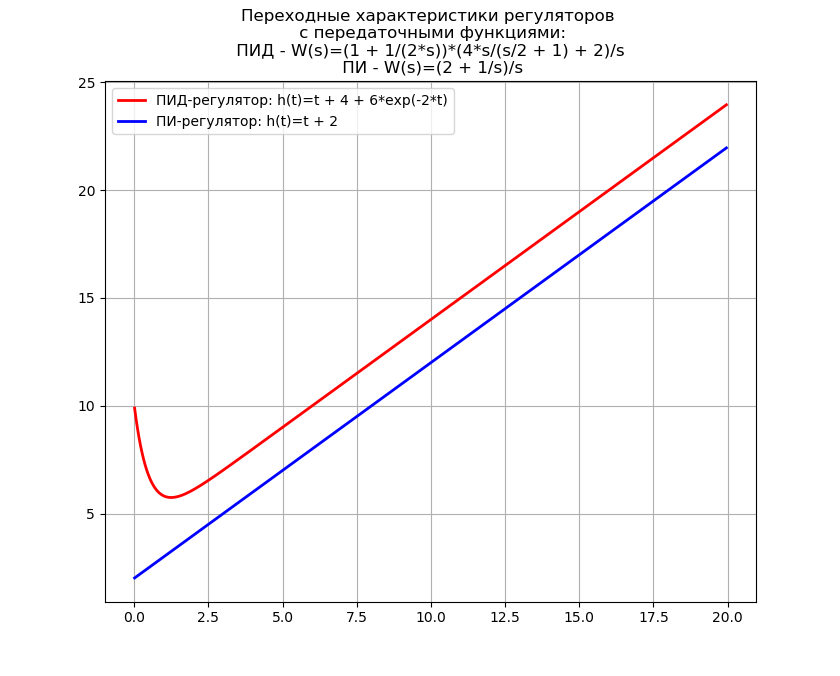
उलटा लाप्लास परिवर्तन अक्सर स्व-चालित बंदूकों के संश्लेषण में उपयोग किया जाता है, जहां पाइथन, MathCAD जैसे महंगे सॉफ़्टवेयर "राक्षसों" को बदल सकता है, इसलिए उलटा परिवर्तन का उपरोक्त उपयोग व्यावहारिक महत्व का है।
कैपुसी समस्या को हल करने के लिए उच्च आदेशों के डेरिवेटिव से लाप्लास रूपांतरित होता है
फार्म के निरंतर गुणांक के साथ रैखिक अंतर समीकरण के समाधान की खोज के लिए लाप्लास ट्रांसफॉर्म (लाप्लास इमेज) के आवेदन के साथ हमारी चर्चा जारी रहेगी:
a cdotx″(t)+b cdotx′(t)+c cdotx(t)=f(t)।(१)
यदि
ए और
बी स्थिरांक हैं, तो
L \ left \ {a \ cdot f (t) + b \ cdot q (t) \ right \} = a \ cdot L \ left \ {f (t) \ right \} + b \ cdot L \ left \ _ {q (t) \ right \} (2)
सभी के लिए ऐसा है कि दोनों लाप्लास कार्य
(च) और
क्ष (टी) के लाप्लास छवि को बदल देते हैं।
आइए हम पहले से
माने गए कार्यों
laplace_transform () और
inverse_laplace_transform () का उपयोग करके प्रत्यक्ष और व्युत्क्रम लाप्लास
रूपांतरों की रैखिकता को सत्यापित करते हैं। इसके लिए, हम उदाहरण के लिए
f (t) = sin (3t) ,
q (t) = cos (7t) ,
a = 5 ,
b = 7 लेते हैं और निम्न प्रोग्राम का उपयोग करते हैं।
कार्यक्रम का पाठ from sympy import* var('sa b') var('t', positive=True) a = 5 f = sin(3*t) b = 7 q = cos(7*t)
हमें मिलता है:(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
(7 * s ** 3 + 15 * s ** 2 + 63 * s + 735) / ((s ** 2 + 9) * (s ** 2 + 49))
यह सच है
5 * पाप (3 * t) + 7 * cos (7 * t)
5 * पाप (3 * t) + 7 * cos (7 * t)
उपरोक्त कोड उलटा लाप्लास परिवर्तन की विशिष्टता को भी प्रदर्शित करता है।
यह मानते हुए कि
q(t)=f′(t) पहले प्रमेय की शर्तों को संतुष्ट करता है, फिर इस प्रमेय से यह निम्नलिखित होगा:
L \ left \ {f '' (t) \ right \} = L \ left \ {q '(t) \ right \} = sL \ left \ {q (t) \ right \} - q (0) = sL \ left \ {f '(t) \ right \} - f' (0) = s \ left [sL \ left \ {f (t) -f (0) \ right \} \ right],
और इस प्रकार
L \ left \ {f '' (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f '(0) $
इस गणना को दोहराते हुए
L \ left \ {f '' '(t) \ right \} = sL \ left \ {f' '(t) \ right \} - f ’’ (0) = s ^ {3} F (s) -s ^ {2} f (0) -sf '(0) -f' '(0)
इस तरह के चरणों की एक सीमित संख्या के बाद, हम पहले प्रमेय के सामान्यीकरण को प्राप्त करते हैं:
L \ left \ {f ^ {(n)} (t) \ right \} = s ^ {n} L \ left \ {f (t) \ right \} - s ^ {n-1} f (0) ) -s ^ {n-2} f '(0) - \ cdot \ cdot \ cdot -f ^ {{(n-1)} (0) =
=snF(s)−sn−1f(0)− cdot cdot cdot−sf(n−2)(0)−f(n−)1)(0)।(३)
संबंध (3) को लागू करना, प्रारंभिक स्थितियों के साथ वांछित फ़ंक्शन के लैप्लस-ट्रांसफ़ॉर्म किए गए डेरिवेटिव, समीकरण (1) के साथ, हम सिम्पोपो लाइब्रेरी के लिए
स्कोरोबी के सक्रिय समर्थन के साथ हमारे विभाग में विशेष रूप से विकसित विधि के अनुसार इसका समाधान प्राप्त कर सकते हैं।
लाप्लास पर आधारित रेखीय अंतर समीकरणों और समीकरणों की प्रणालियों को हल करने के लिए एक विधि SymPy लाइब्रेरी का उपयोग करके बदल देती है
विधि का प्रदर्शन करने के लिए, हम एक साधारण अंतर समीकरण का उपयोग करते हैं जो किसी दिए गए द्रव्यमान के भौतिक बिंदु से युक्त एक प्रणाली की गति का वर्णन करता है, जो एक वसंत पर घुड़सवार होता है, जिसमें एक बाहरी बल लगाया जाता है। इस तरह की प्रणाली के लिए विभेदक समीकरण और प्रारंभिक स्थितियों का रूप है:
x″+4x= sin(3t);x(0)=1.2;x′(0)=1,(4)
जहाँ
x(0) - द्रव्यमान की प्रारंभिक स्थिति कम हो गई,
x′(0) - प्रारंभिक जन वेग कम।
एक साधारण भौतिक मॉडल जो गैर-आरंभिक स्थितियों के साथ समीकरण (4) द्वारा परिभाषित है [1]:
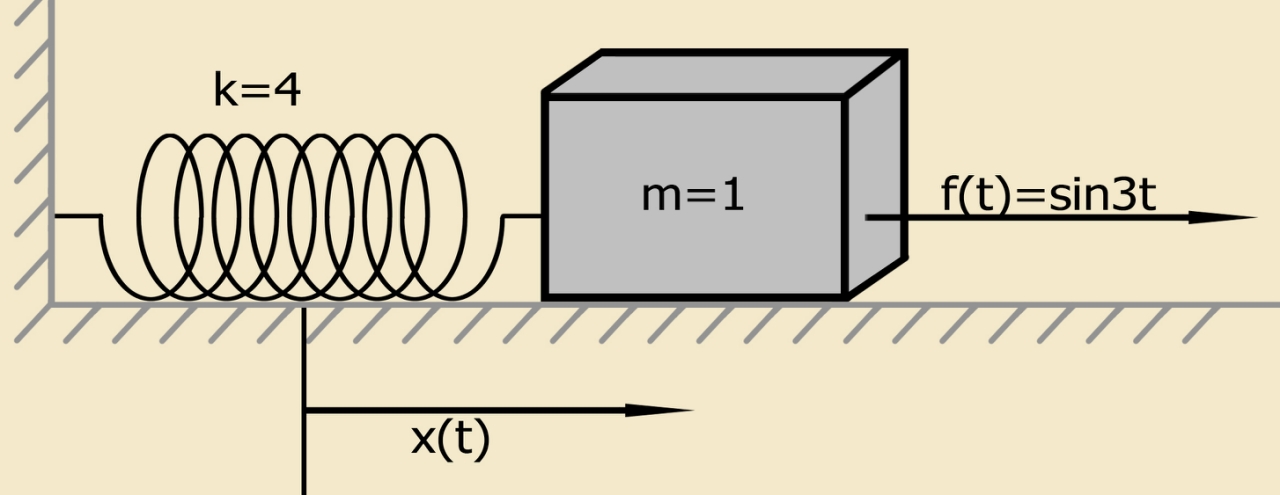
स्प्रिंग पर तय किए गए द्रव्यमान के भौतिक बिंदु से युक्त प्रणाली कॉची समस्या (प्रारंभिक स्थितियों के साथ एक समस्या) को संतुष्ट करती है। किसी दिए गए द्रव्यमान का भौतिक बिंदु शुरू में अपनी संतुलन स्थिति में आराम करता है।
लाप्लास ट्रांसफ़ॉर्म विधि द्वारा इसे और अन्य रैखिक अंतर समीकरणों को हल करने के लिए, संबंधों से प्राप्त निम्नलिखित प्रणाली का उपयोग करना सुविधाजनक है (3):
L \ left \ {f ^ {IV} (t) \ right \} = s ^ {4} \ cdot F (s) -s ^ {3} \ cdot f (0) -s ^ {2} \ cdot f ^ {I} (0) -s \ cdot f ^ {II} (0) -f ^ {III} (0),L \ left \ {f ^ {III} (t) \ right \} = s ^ {3} \ cdot f (s) -s ^ {2} \ cdot f (0) -s \ cdot f ^ {I } (0) -f ^ {II} (0),L \ left \ {f ^ {II} (t) \ right \} = s ^ {2} \ cdot F (s) -s \ cdot f (0) -f ^ {I} (0),L \ left \ {f ^ {I} (t) \ right \} = s \ cdot F (s) -f (0), L \ left \ {f (t) \ right \} = F (s) ।L \ left \ {f (t) \ right \} = F (s)। (५)SymPy का उपयोग करते हुए समाधान का क्रम इस प्रकार है:
- आवश्यक मॉड्यूल लोड करें और स्पष्ट रूप से प्रतीकात्मक चर को परिभाषित करें:
from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
- इसकी विशेषताओं को ध्यान में रखने के लिए सिम्पी लाइब्रेरी का संस्करण निर्दिष्ट करें। ऐसा करने के लिए, निम्नलिखित पंक्तियाँ दर्ज करें:
import SymPy print (' sympy – %' % (sympy._version_))
- समस्या के भौतिक अर्थ के अनुसार, समय चर शून्य और सकारात्मक संख्याओं सहित एक क्षेत्र के लिए निर्धारित किया जाता है। हम प्रारंभिक स्थितियों और फ़ंक्शन को इसके बाद के लाप्लास परिवर्तन के साथ समीकरण (4) के दाईं ओर सेट करते हैं। प्रारंभिक स्थितियों के लिए, आपको एक त्रुटि में दशमलव राउंडिंग परिणामों का उपयोग करने के बाद, तर्कसंगत फ़ंक्शन का उपयोग करना चाहिए।
- (5) का उपयोग करते हुए, हम समीकरण के बाईं ओर में शामिल लाप्लास-परिवर्तित डेरिवेटिव को फिर से लिखते हैं (4), उनसे इस समीकरण के बाईं ओर का निर्माण करते हैं, और इसके दाईं ओर के परिणाम की तुलना करते हैं:
d2 = s**2*X(s) - s*x0 - x01 d0 = X(s) d = d2 + 4*d0 de = Eq(d, Lg)
- हम परिवर्तन एक्स (एस) के लिए प्राप्त बीजीय समीकरण को हल करते हैं और उलटा लाप्लास रूपांतरण करते हैं:
rez = solve(de, X(s))[0] soln = inverse_laplace_transform(rez, s, t)
- हम SymPy लाइब्रेरी में काम से NumPy लाइब्रेरी में ट्रांसफर करते हैं:
f = lambdify(t, soln, 'numpy')
- हम सामान्य पायथन विधि की साजिश करते हैं:
x = np.linspace(0, 6*np.pi, 100) plt.title(', \n :\n (t)=%s' % soln) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2) plt.show()
कार्यक्रम का पूरा पाठ: from sympy import * import numpy as np import matplotlib.pyplot as plt import sympy var('s') var('t', positive=True) var('X', cls=Function) print (" sympy – %s" % (sympy.__version__))
हमें मिलता है:सिम्पी लाइब्रेरी संस्करण - 1.3
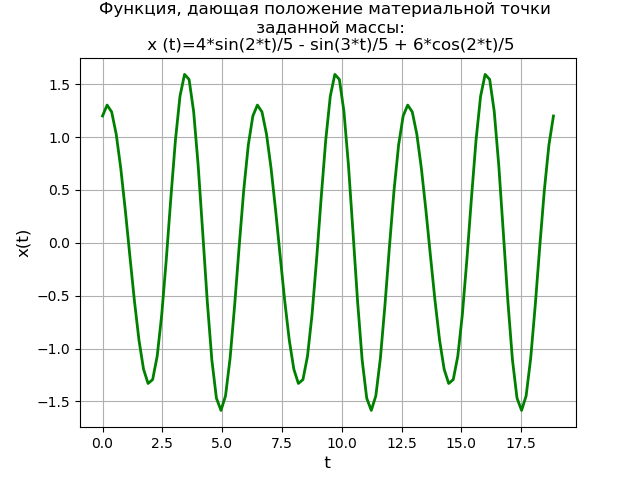
किसी दिए गए द्रव्यमान के भौतिक बिंदु की स्थिति देने वाले आवधिक कार्य का एक ग्राफ प्राप्त किया जाता है। SymPy लाइब्रेरी का उपयोग करते हुए लाप्लास ट्रांसफ़ॉर्म विधि एक समाधान देती है जो न केवल पहले एक सजातीय समीकरण का एक सामान्य समाधान और प्रारंभिक विषम अंतर समीकरण के लिए एक विशेष समाधान खोजने की आवश्यकता के बिना, बल्कि प्राथमिक अंश विधि और लाप्लास तालिकाओं का उपयोग करने की आवश्यकता के बिना भी एक समाधान देता है।
एक ही समय में, समाधान पद्धति का शैक्षिक मूल्य प्रणाली (5) का उपयोग करने की आवश्यकता के कारण संरक्षित है और अधिक उत्पादक तरीकों का उपयोग करके समाधान का अध्ययन करने के लिए NumPy पर जाएं।
आगे विधि प्रदर्शित करने के लिए, हम अंतर समीकरणों की प्रणाली को हल करते हैं:
शुरूमामलों2x″6x−2=0,y″−2x+2y=40 cdot sin(3t), अंतमामलों(6)प्रारंभिक स्थितियों के साथ
x(0)=y(0)=y′(0)=0.शून्य प्रारंभिक परिस्थितियों में समीकरणों की प्रणाली (6) द्वारा परिभाषित एक सरलीकृत भौतिक मॉडल:

इस प्रकार, बल
f (t) को किसी दिए गए द्रव्यमान के दूसरे भौतिक बिंदु पर समय
t = 0 पर लागू किया जाता है, जब सिस्टम अपने संतुलन की स्थिति में आराम पर होता है।
समीकरणों की प्रणाली का समाधान अंतर समीकरण (4) के पहले से माना समाधान के समान है, इसलिए, मैं स्पष्टीकरण के बिना कार्यक्रम का पाठ देता हूं।
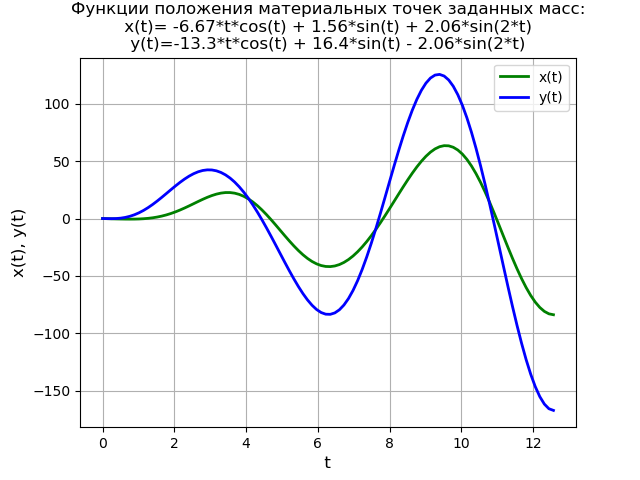
कार्यक्रम का पाठ from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t ', positive=True) var('X Y', cls=Function) x0 = 0 x01 = 0 y0 = 0 y01 = 0 g = 40 * sin(3*t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = inverse_laplace_transform(rezX, s, t) rezY = expand(rez[Y(s)]) solnY = inverse_laplace_transform(rezY, s, t) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)=%s\ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
हमें मिलता है: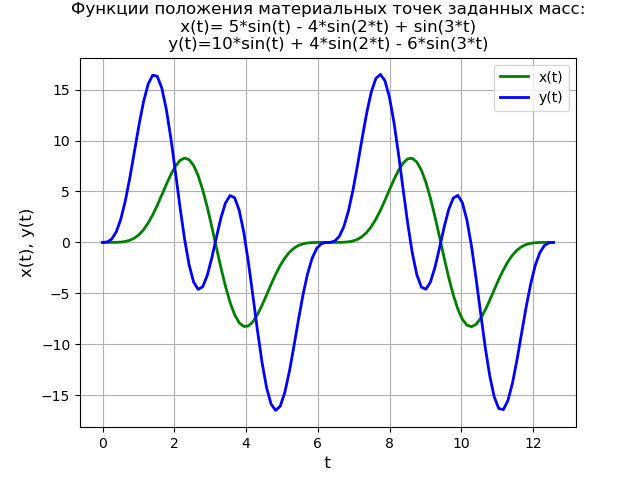
नॉनज़ेरो प्रारंभिक स्थितियों के लिए, प्रोग्राम टेक्स्ट और फ़ंक्शन ग्राफ फॉर्म लेगा:
कार्यक्रम का पाठ from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X Y', cls=Function) x0 = 0 x01 = -1 y0 = 0 y01 = -1 g = 40 * sin(t) Lg = laplace_transform(g, t, s, noconds=True) de1 = Eq(2*(s**2*X(s) - s*x0 - x01) + 6*X(s) - 2*Y(s)) de2 = Eq(s**2*Y(s) - s*y0 - y01 - 2*X(s) + 2*Y(s) - Lg) rez = solve([de1, de2], X(s), Y(s)) rezX = expand(rez[X(s)]) solnX = (inverse_laplace_transform(rezX, s, t)).evalf().n(3) rezY = expand(rez[Y(s)]) solnY = (inverse_laplace_transform(rezY, s, t)).evalf().n(3) f = lambdify(t, solnX, "numpy") F = lambdify(t, solnY, "numpy") x = np.linspace(0, 4*np.pi, 100) plt.title(' :\nx(t)= %s \ny(t)=%s' % (solnX, solnY)) plt.grid(True) plt.xlabel('t', fontsize=12) plt.ylabel('x(t), y(t)', fontsize=12) plt.plot(x, f(x), 'g', linewidth=2, label='x(t)') plt.plot(x, F(x), 'b', linewidth=2, label='y(t)') plt.legend(loc='best') plt.show()
शून्य-प्रारंभिक स्थितियों के साथ चौथे क्रम के रैखिक अंतर समीकरण के समाधान पर विचार करें:
x(4)+2 cdotx″+x=4 cdott cdote;x(0)=x′(0)=x″(0)=x(3)(0)=कार्यक्रम का पाठ: from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
निर्णय अनुसूची:
हम चौथे क्रम के रैखिक अंतर समीकरण को हल करते हैं:
x(4)+13x″+36x=0;प्रारंभिक स्थितियों के साथ
x(0)=x″(0)=0 ।
x′(0)=2 ।
x(3)(0)=−13 ।
कार्यक्रम का पाठ: from sympy import * import numpy as np import matplotlib.pyplot as plt var('s') var('t', positive=True) var('X', cls=Function)
निर्णय अनुसूची: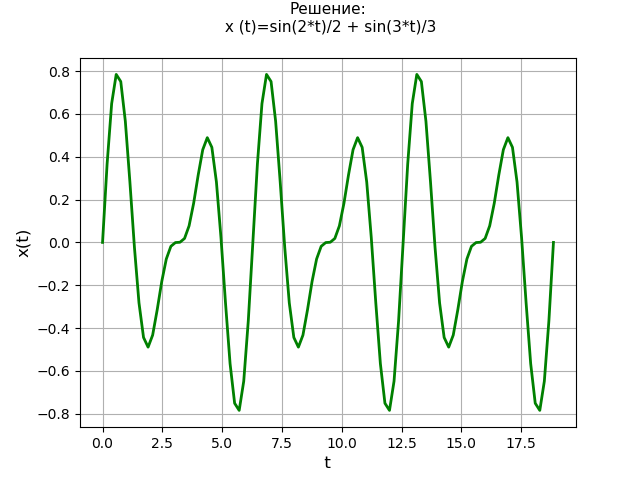
ODE को हल करने के लिए कार्य
विश्लेषणात्मक समाधान के साथ ODE और ODE सिस्टम के लिए,
dsolve () फ़ंक्शन का उपयोग किया जाता है:
sympy.solvers.ode।
dsolve (eq, func =
none , hint = 'default',
simple =
true , ics = कोई नहीं, xi = कोई नहीं, eta = कोई नहीं, x0 = 0, n = 6, ** kwargs)
चलो लाप्लास विधि के साथ dsolve () फ़ंक्शन के प्रदर्शन की तुलना करें। उदाहरण के लिए, शून्य प्रारंभिक स्थितियों के साथ निम्नलिखित चौथे-डिग्री के अंतर समीकरण को लें:
x(IV)(t)=3 cdotx‴(t)−x(t)=4 cdott cdot exp(t);x(0)=x′(0)=x″(0)=x‴(0)=0.Dsolve () फ़ंक्शन का उपयोग करके एक प्रोग्राम: from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('t C1 C2 C3 C4') u = Function("u")(t)
हमें मिलता है:Dsolve () फ़ंक्शन: 1.437 s का उपयोग कर समीकरण समय
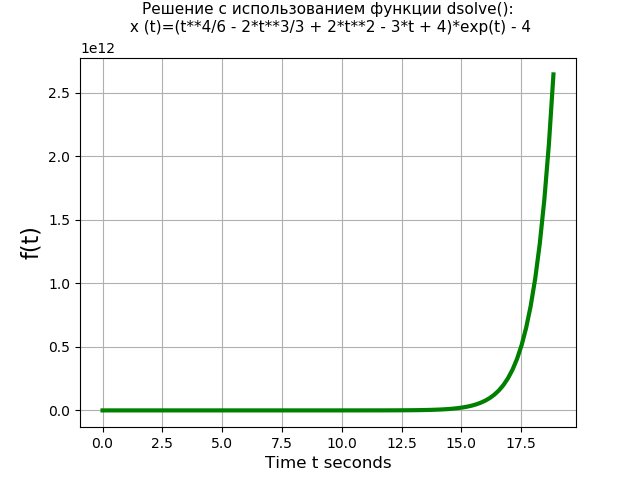
लाप्लास ट्रांसफ़ॉर्म का उपयोग करके कार्यक्रम: from sympy import * import time import numpy as np import matplotlib.pyplot as plt start = time.time() var('s') var('t', positive=True) var('X', cls=Function)
हमें मिलता है:लैप्लस परिवर्तन का उपयोग कर समीकरण समय: 3.274 एस

तो, dsolve () फ़ंक्शन (1.437 s) दो बार से अधिक लाप्लास ट्रांसफॉर्म विधि (3.274 s) द्वारा हल करने की तुलना में चौथे क्रम के समीकरण को तेजी से हल करता है। हालांकि, यह ध्यान दिया जाना चाहिए कि dsolve () फ़ंक्शन दूसरे-क्रम के अंतर समीकरणों की प्रणाली को हल नहीं करता है, उदाहरण के लिए, जब dsolve () फ़ंक्शन का उपयोग करके सिस्टम (6) को हल करते हैं, तो एक त्रुटि होती है:
from sympy import* t = symbols('t') x, y = symbols('x, y', Function=True) eq = (Eq(Derivative(x(t), t, 2), -3*x(t) + y(t)), Eq(Derivative(y(t), t, 2), 2*x(t) - 2*y(t) + 40*sin(3*t))) rez = dsolve(eq) print (list(rez))
हमें मिलता है:raiseNotImplementedError
NotImplementedError
इस त्रुटि का अर्थ है कि
dsolve () फ़ंक्शन का उपयोग करके अंतर समीकरणों की प्रणाली का समाधान प्रतीकात्मक रूप से नहीं
दिखाया जा सकता है। जबकि लाप्लास रूपांतरों की मदद से हमें समाधान का एक प्रतीकात्मक प्रतिनिधित्व मिला, और यह प्रस्तावित पद्धति की प्रभावशीलता को साबित करता है।
नोट।Dsolve () फ़ंक्शन का उपयोग करके अंतर समीकरणों को हल करने के लिए आवश्यक विधि खोजने के लिए, आपको उदाहरण के लिए
classify_ode (eq, f (x)) का उपयोग
करने की आवश्यकता है:
from sympy import * from IPython.display import * import matplotlib.pyplot as plt init_printing(use_latex=True) x = Symbol('x') f = Function('f') eq = Eq(f(x).diff(x, x) + f(x), 0) print (dsolve(eq, f(x))) print (classify_ode(eq, f(x))) eq = sin(x)*cos(f(x)) + cos(x)*sin(f(x))*f(x).diff(x) print (classify_ode(eq, f(x))) rez = dsolve(eq, hint='almost_linear_Integral') print (rez)
हमें मिलता है:Eq (f (x), C1 * sin (x) + C2 * cos (x))
('nth_linear_constant_coeff_homogeneous', '2nd_power_series_ordinary')
('वियोज्य', '1st_exact', 'लगभग_लाइनर', '1st_power_series', 'lie_group', 'विभाजनीय_इंटरग्रील', '1st_exact_Integral', 'लगभग_लाइनियर_इंटरग्रल')
[Eq (f (x), -acos ((C1 + इंटीग्रल (0, x)) * exp (-Integral (-tan (x), x))) + 2 * pi), Eq (f (x),) acos ((C1 + इंटीग्रल (0, x)) * exp (-Ingrgral (-tan (x), x)))]]
इस प्रकार, समीकरण के लिए
eq = Eq (f (x) .diff (x, x) + f (x), 0) , पहली सूची के किसी भी तरीके से काम करता है:
nth_linear_constant_coeff_homogeneous,
2nd_power_series_ordinary
समीकरण के लिए
eq = sin (x) * cos (f (x)) + cos (x) * sin (f (x)) * f (x)। Diff (x) , दूसरी सूची के किसी भी तरीके से काम करता है:
वियोज्य, 1st_exact, लगभग_लीनियर,
1st_power_series, lie_group, जुदाई_इंटरग्रल,
1st_exact_Integral, लगभग_linear_Integral
चयनित विधि का उपयोग करने के लिए, dsolve () फ़ंक्शन प्रविष्टि फॉर्म को ले जाएगी, उदाहरण के लिए:
rez = dsolve(eq, hint='almost_linear_Integral')
निष्कर्ष:
इस लेख का उद्देश्य यह दिखाना है कि ऑपरेटर विधि का उपयोग करके रैखिक ODE सिस्टम को हल करने के उदाहरण पर SciPy और NumPy पुस्तकालयों के उपकरण का उपयोग कैसे करें। इस प्रकार, रैखिक अंतर समीकरणों के प्रतीकात्मक समाधान के तरीकों और लाप्लास विधि द्वारा समीकरणों की प्रणालियों पर विचार किया गया था। इस विधि और dsolve () फ़ंक्शन में कार्यान्वित विधियों का प्रदर्शन विश्लेषण किया जाता है।
संदर्भ:- विभेदक समीकरण और सीमा मूल्य की समस्याएं: मॉडलिंग और गणितज्ञ, मेपल और MATLAB का उपयोग करके गणना। तीसरा संस्करण ।: प्रति। अंग्रेजी से - एम।: एलएलसी “आई.डी. विलियम्स, 2008. - 1104 पी .: बीमार। - पराल। तैसा। अभियांत्रिकी।
- व्युत्क्रम लाप्लास परिवर्तन का उपयोग नियंत्रण प्रणालियों के गतिशील लिंक का विश्लेषण करने के लिए