ओपनजीएल जानें। पाठ 6.1। PBR या शारीरिक रूप से सही प्रतिपादन। सिद्धांत

शारीरिक रूप से सही प्रतिपादन

पीबीआर, या शारीरिक रूप से आधारित प्रतिपादन, एक सिद्धांत पर आधारित दृश्य तकनीकों का एक सेट है जो प्रकाश प्रसार के वास्तविक सिद्धांत से काफी सहमत है। चूंकि पीबीआर का उद्देश्य प्रकाश का एक शारीरिक रूप से विश्वसनीय अनुकरण है, यह फोंग और ब्लिन-फोंग प्रकाश मॉडल की तुलना में बहुत अधिक यथार्थवादी दिखता है जो हमने पहले इस्तेमाल किया था। यह न केवल बेहतर दिखता है, बल्कि वास्तविक भौतिकी को भी एक अच्छा सन्निकटन देता है, जो हमें (और कलाकारों को) विशेष रूप से सतहों के भौतिक गुणों के आधार पर सामग्री बनाने की अनुमति देता है, ताकि प्रकाश को यथार्थवादी बनाने के लिए सस्ती चाल का सहारा न लिया जा सके। इस दृष्टिकोण का मुख्य लाभ यह है कि हमारे द्वारा बनाई गई सामग्री प्रकाश की स्थिति की परवाह किए बिना नियोजित दिखेगी, जिसे अन्य के बारे में नहीं कहा जा सकता है, न कि पीबीआर, दृष्टिकोण।

हालांकि, पीबीआर अभी भी वास्तविकता का एक अनुमान है (भौतिकी के नियमों के आधार पर), यही वजह है कि इसे शारीरिक रूप से सही प्रतिपादन कहा जाता है, भौतिक प्रतिपादन नहीं। ताकि प्रकाश मॉडल को शारीरिक रूप से सही कहा जा सके, इसे 3 शर्तों को पूरा करना होगा (चिंता न करें, हम जल्द ही उनसे मिलेंगे):

• चिंतनशील सूक्ष्म चेहरों के एक मॉडल पर आधारित है
• ऊर्जा के संरक्षण के नियम का पालन करें
• डबल-बीम प्रतिबिंब वितरण फ़ंक्शन (BRDF) का उपयोग करें

इस ट्यूटोरियल श्रृंखला में, हम पीबीआर दृष्टिकोण पर ध्यान केंद्रित करेंगे, जो मूल रूप से डिज्नी में विकसित किया गया था और एपिक गेम्स द्वारा वास्तविक समय के दृश्य के लिए अनुकूलित किया गया था। धातु-ढांकता हुआ वर्कफ़्लो (इंजी। मेटैलिक वर्कफ़्लो) पर आधारित उनका दृष्टिकोण, बेहतर अनुवाद नहीं ढूँढ सकता है - लगभग। एड। ), अच्छी तरह से प्रलेखित है, व्यापक रूप से कई लोकप्रिय इंजनों में स्वीकार किया जाता है और अद्भुत दिखता है। इस खंड के अंत में, हमें इसके समान कुछ मिलता है:

ध्यान रखें कि इस खंड के लेख काफी उन्नत हैं, इसलिए यह अनुशंसा की जाती है कि आपको ओपनजीएल और शेडर लाइटिंग की अच्छी समझ हो। इस खंड में आपको कुछ ज्ञान का अध्ययन करना होगा: फ्रेम बफर , क्यूबिक मैप्स , गामा करेक्शन , एचडीआर, और सामान्य मैप्स । हम गणित में भी थोड़ा गहराई से जाएंगे, लेकिन मैं हर चीज को यथासंभव स्पष्ट रूप से समझाने के लिए हर संभव प्रयास करने का वादा करता हूं।

चिंतनशील सूक्ष्म पहलुओं का मॉडल

सभी PBR तकनीक सूक्ष्म चेहरों के सिद्धांत पर आधारित हैं। यह सिद्धांत कहता है कि उच्च आवर्धन पर प्रत्येक सतह को सूक्ष्म चेहरे के सूक्ष्म दर्पण के एक सेट के रूप में दर्शाया जा सकता है। सतह खुरदरापन के कारण, ये सूक्ष्म दर्पण विभिन्न दिशाओं में उन्मुख हो सकते हैं:

सतह जितनी खुरदरी होती है, उतनी ही बेतरतीब ढंग से उसके सूक्ष्म चेहरे उन्मुख होते हैं। इन छोटे दर्पणों की इस व्यवस्था का परिणाम है (विशेष रूप से जब यह स्पेक्युलर फ्लेयर्स और रिफ्लेक्शंस की बात आती है) कि रौशनी की घटना किरणें खुरदरी सतहों पर अलग-अलग दिशाओं में बिखरी होती हैं, जिससे व्यापक स्पेकुलर फ्लेयर होता है। और इसके विपरीत: चिकनी सतहों पर, घटना किरणों को एक दिशा में परिलक्षित होने की अधिक संभावना है, जो एक छोटी और तेज चमक देगा:

सूक्ष्म स्तर पर, बिल्कुल चिकनी सतह नहीं होती हैं, लेकिन यह देखते हुए कि सूक्ष्म चेहरे काफी छोटे हैं और हम अपने पिक्सेल स्थान के भीतर उनके बीच अंतर नहीं कर सकते हैं, हम एक खुरदरापन गुणांक पेश करके सतह खुरदरापन का अनुमान लगाते हैं। इस गुणांक का उपयोग करके, हम एक निश्चित वेक्टर की दिशा में उन्मुख सूक्ष्म चेहरों के अंश की गणना कर सकते हैं $$$ज$ । यह सदिश $$$ज$ घटना प्रकाश की दिशा के बीच बीच में पड़े एक मध्ययुगीन वेक्टर से ज्यादा कुछ नहीं $$$ल$ और प्रेक्षक की दिशा $$$वी$ । हमने पहले उन्नत प्रकाश व्यवस्था पर एक पाठ में इसके बारे में बात की, जहां हमने इसे वैक्टर के योग के अनुपात के रूप में परिभाषित किया $$$ल$ और $$$वी$ परिणामस्वरूप वेक्टर की लंबाई:

$$

$$h = \ frac {l + v} {|| l + v ||}$$

मंझला वेक्टर की दिशा में जितना अधिक सूक्ष्म चेहरे उन्मुख होंगे, उतना ही तेज और चमकीला स्पेक्युलर हाइलाइट होगा। खुरदरापन गुणांक के कारण, जो 0 और 1 के बीच स्थित है, हम सूक्ष्म चेहरे के उन्मुखीकरण को सांख्यिकीय रूप से अनुमानित कर सकते हैं:

जैसा कि आप देख सकते हैं, खुरदरापन गुणांक का एक उच्च मूल्य चिकनी सतहों पर एक छोटे और तेज स्थान की तुलना में एक बड़े आकार का एक मिरर फ्लेयर स्पॉट देता है।

ऊर्जा संरक्षण।

सूक्ष्म चेहरे को ध्यान में रखते हुए सन्निकटन का उपयोग करने से पहले से ही ऊर्जा संरक्षण का एक निश्चित रूप होता है: परावर्तित प्रकाश की ऊर्जा कभी भी प्रकाश की ऊर्जा से अधिक नहीं होगी (यदि सतह खुद से चमकती नहीं है)। ऊपर की छवि को देखते हुए, हम देखते हैं कि सतह की खुरदरापन में वृद्धि के साथ, परावर्तित प्रकाश का स्थान बढ़ता है, लेकिन एक ही समय में इसकी चमक कम हो जाती है। यदि परावर्तित प्रकाश की तीव्रता स्पॉट के आकार की परवाह किए बिना सभी पिक्सल के लिए समान थी, तो मोटे तौर पर सतह अधिक ऊर्जा का उत्सर्जन करेगी, जो ऊर्जा के संरक्षण के कानून का उल्लंघन करेगी। इसलिए, स्पेक्युलर परावर्तन चिकनी सतहों पर चमकीले और खुरदरी सतहों पर मंद होते हैं।

ऊर्जा को संरक्षित करने के लिए, हमें फैलाना और दर्पण घटकों के बीच स्पष्ट अलगाव करना चाहिए। उस क्षण में, जब प्रकाश की एक किरण सतह तक पहुंचती है, तो यह परावर्तित और अपवर्तित घटकों में विभाजित होती है । परावर्तित घटक प्रकाश परावर्तित होता है और सतह में प्रवेश नहीं करता है; हम इसे प्रकाश के दर्पण घटक के रूप में जानते हैं। अपवर्तित घटक प्रकाश है जो सतह में प्रवेश करता है और इसके द्वारा अवशोषित होता है - यह हमें प्रकाश के फैलाने वाले घटक के रूप में जाना जाता है।

लेकिन प्रकाश के अवशोषण से जुड़ी कुछ बारीकियां हैं - यह तुरंत नहीं होता है, जैसे ही प्रकाश सतह को छूता है। भौतिकी के पाठ्यक्रम से, हम जानते हैं कि प्रकाश को ऊर्जा के साथ फोटोन के एक बीम के रूप में वर्णित किया जा सकता है जो एक सीधी रेखा में चलता है जब तक कि यह बाधाओं के साथ टकराव के परिणामस्वरूप सभी ऊर्जा खो देता है। प्रत्येक सामग्री में माइक्रोपार्टिकल्स होते हैं जो प्रकाश की किरण के साथ बातचीत कर सकते हैं, जैसा कि नीचे की आकृति में दिखाया गया है। ये कण हर टकराव में प्रकाश की ऊर्जा के भाग या सभी को अवशोषित करते हैं, इसे गर्मी में परिवर्तित करते हैं।

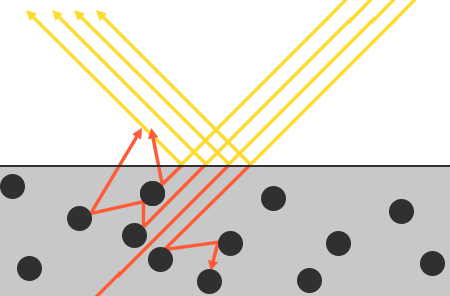
सामान्य स्थिति में, सभी ऊर्जा अवशोषित नहीं होती है, और प्रकाश लगातार (मुख्य रूप से) यादृच्छिक दिशाओं में बिखरता रहता है, जहां यह फिर से अन्य कणों से टकराता है जब तक कि यह ऊर्जा से बाहर नहीं निकलता है या फिर सतह को छोड़ देता है। इस प्रकार, सतह प्रकाश किरणों को फिर से उत्सर्जित करने के लिए शुरू होती है, सतह के मनाया (फैलाना) रंग के रूप में योगदान देता है। पीबीआर का उपयोग करते हुए, हम सरल धारणा बनाते हैं कि सभी अपवर्तित प्रकाश प्रभाव के एक छोटे से क्षेत्र में अवशोषित और बिखरे हुए हैं, इस क्षेत्र से दूरी पर सतह को छोड़ने वाले बिखरे हुए प्रकाश के प्रभाव को अनदेखा करते हैं। विशेष shader तकनीक जो इसे ध्यान में रखते हैं, उपसतह बिखरने वाली तकनीकों के रूप में जानी जाती हैं, चमड़े, संगमरमर, मोम जैसी सामग्रियों की दृश्य गुणवत्ता को बहुत बढ़ाती हैं, लेकिन प्रदर्शन के मामले में महंगी हैं।

अतिरिक्त सूक्ष्मताएं तब दिखाई देती हैं जब प्रकाश का अपवर्तन होता है और धातु की सतहों पर परिलक्षित होता है। धातु की सतहें गैर-धात्विक (यानी, डाइलेट्रिक्स) की तुलना में प्रकाश के साथ अलग - अलग तरीके से संपर्क करती हैं। वे अपवर्तन और परावर्तन के समान नियमों का पालन करते हैं, एक अपवाद के साथ: सभी अपवर्तित प्रकाश को बिखरने के बिना सतह द्वारा अवशोषित किया जाता है, केवल दर्पण-प्रतिबिंबित प्रकाश अवशेष; दूसरे शब्दों में, धातु की सतहों का रंग फैलता नहीं है। धातुओं और डाइलेक्ट्रिक्स के बीच इस स्पष्ट अंतर के कारण, उन्हें PBR कन्वेयर में अलग तरीके से संसाधित किया जाएगा, जिसमें हम इस लेख के पाठ्यक्रम को और नीचे ले जाएंगे।

प्रतिबिंबित और अपवर्तित प्रकाश के बीच यह अंतर हमें ऊर्जा संरक्षण के संबंध में एक और अवलोकन की ओर ले जाता है: उनके मूल्य परस्पर अनन्य हैं। प्रतिबिंबित प्रकाश की ऊर्जा को सामग्री द्वारा अवशोषित नहीं किया जा सकता है। इसलिए, परावर्तित प्रकाश के रूप में सतह द्वारा अवशोषित ऊर्जा प्रतिबिंबित प्रकाश के लिए लेखांकन के बाद शेष ऊर्जा है।
हम इस अनुपात का उपयोग करते हैं, सतह द्वारा परावर्तित किरणों की ऊर्जा के प्रतिशत के रूप में पहले परिलक्षित भाग की गणना करते हैं, और फिर परावर्तित प्रकाश का अंश सीधे परावर्तित से, जैसे:

float kS = calculateSpecularComponent(...); // /  float kD = 1.0 - kS; // /  

इस तरह हम ऊर्जा के संरक्षण के नियम के लिए परिलक्षित और अपवर्तित दोनों भागों के अर्थ सीखते हैं। इस दृष्टिकोण के साथ, न तो अपवर्तित (फैलाना) और न ही परिलक्षित भाग 1.0 से अधिक होगा, यह सुनिश्चित करते हुए कि उनकी कुल ऊर्जा घटना प्रकाश ऊर्जा के मूल्य से अधिक नहीं है, जिसे हम पिछले पाठों में ध्यान में नहीं ले सकते थे।

परावर्तन समीकरण

उपरोक्त हमें तथाकथित प्रतिपादन समीकरण की ओर ले जाता है : बहुत स्मार्ट लोगों द्वारा आविष्कार किया गया एक जटिल समीकरण, और आज यह अनुकरण प्रकाश व्यवस्था के लिए सबसे अच्छा मॉडल है। PBR इस समीकरण के कड़ाई से अधिक विशिष्ट संस्करण का अनुसरण करता है, जिसे प्रतिबिंब समीकरण के रूप में जाना जाता है । PBR को अच्छी तरह से समझने के लिए, पहले प्रतिबिंब समीकरण की पूरी समझ होना जरूरी है:

$$

$$L_o (p, \ omega_o) = \ int \ limit_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

पहले तो यह डरावना लग रहा है, लेकिन हम इसे धीरे-धीरे अलग-अलग हिस्सों में ले जाएंगे, और आप देखेंगे कि धीरे-धीरे यह समझ में आने लगेगा। इस समीकरण को समझने के लिए हमें रेडियोमेट्री में थोड़ा गहरा जाना होगा। रेडियोमीट्रिक विद्युत चुम्बकीय विकिरण (दृश्य प्रकाश सहित) को मापने का विज्ञान है। कई रेडियोमेट्रिक मात्राएं हैं जिनका उपयोग हम रोशनी को मापने के लिए कर सकते हैं, लेकिन हम केवल प्रतिबिंब समीकरण से संबंधित एक का उपयोग करेंगे, जिसे एनर्जी ल्यूमिनेंस (अंग्रेजी मूलक) के रूप में जाना जाता है और पत्र द्वारा यहां निर्दिष्ट किया जाता है। एलआई का उपयोग प्रकाश की तीव्रता या तीव्रता को निर्धारित करने के लिए किया जाता है। एक निश्चित दिशा से आ रहा है। EJ, बदले में, कई भौतिक राशियों का एक संयोजन है, और इसलिए कि यह कल्पना करना हमारे लिए आसान है, हम उनमें से प्रत्येक पर व्यक्तिगत रूप से ध्यान केंद्रित करेंगे।

दीप्तिमान प्रवाह

विकिरण प्रवाह ( $$$\ Phi$ ) प्रकाश-संचरित ऊर्जा की शक्ति है, जिसे वाट में मापा जाता है। प्रकाश की कुल ऊर्जा में विभिन्न तरंग दैर्ध्य के लिए कई शब्द होते हैं, जिनमें से प्रत्येक स्पेक्ट्रम के अपने रंग से मेल खाती है। प्रकाश स्रोत द्वारा उत्सर्जित ऊर्जा, इस मामले में, इन सभी तरंग दैर्ध्य के एक समारोह के रूप में प्रतिनिधित्व किया जा सकता है। 390nm से 700nm तक की तरंग दैर्ध्य स्पेक्ट्रम के दृश्य भाग को बनाते हैं, अर्थात, इस सीमा में विकिरण को मानव आंख द्वारा माना जा सकता है। नीचे दी गई छवि में आप विभिन्न तरंग दैर्ध्य के लिए ऊर्जा के मूल्यों को दिन के उजाले में देख सकते हैं:

विकिरण तरंग सभी तरंग दैर्ध्य के लिए इस फ़ंक्शन के ग्राफ के तहत क्षेत्र से मेल खाती है। कंप्यूटर ग्राफिक्स में इनपुट के रूप में प्रकाश की तरंग दैर्ध्य का प्रत्यक्ष उपयोग अव्यावहारिक है, इसलिए हम सभी तरंगदैर्ध्य के एक फ़ंक्शन का उपयोग करने के बजाय, विकिरण के सरलीकृत प्रतिनिधित्व का सहारा लेते हैं, रंगों का एक समूह, जिसे RGB (या, जैसा कि हम आमतौर पर इसे प्रकाश का रंग कहते हैं) कहते हैं। इस तरह के एक दृश्य से जानकारी का कुछ नुकसान होता है, लेकिन पूरे पर यह अंतिम तस्वीर को थोड़ा प्रभावित करेगा।

ठोस कोण

द्वारा निरूपित ठोस कोण $$$\ _ ओमेगा$ हमें इकाई क्षेत्र पर अनुमानित आकृति का आकार या क्षेत्र देता है। आप इसकी एक दिशा के रूप में कल्पना कर सकते हैं:

कल्पना कीजिए कि आप एक गोले के केंद्र में हैं और आकृति की दिशा में देख रहे हैं। परिणामस्वरूप सिल्हूट का आकार एक ठोस कोण होगा।

विकिरण की तीव्रता

विकिरण शक्ति ठोस कोण प्रति विकिरण प्रवाह की मात्रा या ठोस कोण द्वारा परिभाषित प्रति इकाई क्षेत्र में एक प्रकाश स्रोत की ताकत को मापती है। उदाहरण के लिए, एक सर्वव्यापी प्रकाश स्रोत के लिए जो समान रूप से सभी दिशाओं में निकलता है, विकिरण बल का अर्थ है प्रति विशिष्ट क्षेत्र (ठोस कोण) प्रकाश की ऊर्जा:

विकिरण की ताकत का वर्णन करने वाला समीकरण इस तरह दिखता है:

$$

$$I = \ frac {d \ Phi} {d \ omega}$$

, जहां मैं प्रति ठोस कोण पर विकिरण प्रवाह f है $$${d \ omega}$

विकिरण प्रवाह, बल और ठोस कोण को जानकर, हम ऊर्जा चमक समीकरण का वर्णन कर सकते हैं, जो कि क्षेत्र A में कुल देखी गई ऊर्जा का वर्णन करता है, बल द्वारा प्रकाश के लिए ठोस कोण O द्वारा सीमित है। $$$\ Phi$

$$

$$L = \ frac {d ^ 2 \ Phi} {dA d \ omega \ cos \ theta}$$

ऊर्जा चमक एक क्षेत्र में प्रकाश की विकिरणमितीय मात्रा है जो घटना प्रकाश के कोण पर निर्भर करती है। $$$$ थीटा$ (प्रकाश की दिशा और सतह के सामान्य के बीच का कोण) के माध्यम से $$$cos \ थीटा$ : सतह के साथ उत्सर्जित होने पर प्रकाश कमजोर होता है और जब यह लंबवत होता है तो मजबूत होता है। यह प्रकाश की मूल बातें पर ट्यूटोरियल में प्रकाश फैलाने के लिए हमारी गणना के समान है $$$cos \ थीटा$ प्रकाश की दिशा और सतह के सामान्य वेक्टर के बीच एक अदिश उत्पाद से अधिक कुछ नहीं:

 float cosTheta = dot(lightDir, N); 

ऊर्जा की चमक का समीकरण हमारे लिए बहुत उपयोगी है, क्योंकि इसमें अधिकांश भौतिक मात्राएँ हैं जो हमें रुचि देती हैं। यदि हम मानते हैं कि ठोस कोण solid और क्षेत्र A अनंत है, तो हम अंतरिक्ष में प्रति एक बिंदु पर प्रकाश की एक किरण के प्रवाह को मापने के लिए EE का उपयोग कर सकते हैं। यह हमें एक बिंदु (खंड) पर एकल प्रकाश किरण अभिनय के ईआई की गणना करने की अनुमति देगा; हम वास्तव में ठोस कोण का अनुवाद करते हैं $$$\ _ ओमेगा$ दिशा में वेक्टर $$$\ _ ओमेगा$ और $$$ए$ इस बिंदु पर $$$पी$ । इस प्रकार, हम प्रत्येक टुकड़े के लिए एकल प्रकाश किरण के योगदान की गणना करने के लिए सीधे अपने शेड में ईआई का उपयोग कर सकते हैं।

वास्तव में, जब ईई की बात आती है, तो हम आम तौर पर पॉइंट पी पर आने वाली सभी हल्की घटनाओं में रुचि रखते हैं, जो पूरे ईई का योग है, और इसे विकिरण के रूप में जाना जाता है। ईआई और विकिरण को जानने के बाद, हम प्रतिबिंब समीकरण पर लौट सकते हैं:

$$

$$L_o (p, \ omega_o) = \ int \ limit_ \ Omega f_r (p, \ omega_i, \ omega_o) L_i (p, \ omega_i) n \ cdot \ omega_id \ omega_i$$

अब हम जानते हैं कि $$$एल$ रेंडरिंग समीकरण में सतह पी पर कुछ बिंदु और आने वाली रोशनी के कुछ असीम छोटे ठोस कोण के लिए ईआई है $$$\ _ omega_i$ , जिसे इनपुट निर्देश वेक्टर के रूप में माना जा सकता है $$$\ _ omega_i$ । याद रखें कि ऊर्जा कई गुना है $$$cos \ थीटा$ - प्रकाश की घटना और सतह पर सामान्य की दिशा के बीच का कोण, जो उत्पाद द्वारा प्रतिबिंब के समीकरण में व्यक्त किया जाता है $$$n \ cdot \ omega_i$ । प्रतिबिंब समीकरण परिलक्षित ईआई के योग की गणना करता है $$$L_o (p, \ omega_o)$ बिंदु $$$पी$ की दिशा में $$$ω_o$ , जो पर्यवेक्षक के लिए निवर्तमान दिशा है। वरना: $$$L_o$ एक बिंदु के प्रतिबिंबित विकिरण को मापता है $$$पी$ अगर से देखा जाए $$$\ _ omega_o$ ।

चूंकि प्रतिबिंब समीकरण विकिरण पर आधारित है, जो सभी आने वाली विकिरण का योग है, हम प्रकाश को न केवल एक आने वाली प्रकाश दिशा, बल्कि गोलार्ध के भीतर आने वाली सभी प्रकाश दिशाओं से मापते हैं $$$\ _ ओमेगा$ पर केंद्रित है $$$पी$ । इसे सामान्य सतह के साथ आधा गोलाकार कहा जा सकता है $$$एन$ :

क्षेत्र के अंदर सभी मूल्यों के योग की गणना करने के लिए, या गोलार्ध के मामले में, हम सभी आने वाली दिशाओं में समीकरण को एकीकृत करते हैं। $$$d \ omega_i$ गोलार्ध के भीतर $$$\ _ ओमेगा$ । चूंकि रेंडर समीकरण और परावर्तन समीकरण दोनों के लिए कोई विश्लेषणात्मक समाधान नहीं है, इसलिए हम अभिन्न रूप से हल करेंगे। इसका मतलब यह है कि हम गोलार्ध प्रतिबिंब समीकरण के छोटे असतत चरणों के लिए परिणाम प्राप्त करेंगे $$$\ _ ओमेगा$ और उन्हें चरण के आकार पर औसत करें। इसे रीमैन योग कहा जाता है, जिसे हम निम्नलिखित कोड के साथ देख सकते हैं:

 int steps = 100; float sum = 0.0f; vec3 P = ...; vec3 Wo = ...; vec3 N = ...; float dW = 1.0f / steps; for(int i = 0; i < steps; ++i) { vec3 Wi = getNextIncomingLightDir(i); sum += Fr(P, Wi, Wo) * L(P, Wi) * dot(N, Wi) * dW; } 

प्रत्येक असतत कदम के लिए dW के रूप में माना जा सकता है $$$d \ omega_i$ प्रतिबिंब समीकरण में। गणितीय $$$d \ omega_i$ वह अंतर है जिसके द्वारा हम अभिन्न की गणना करते हैं, और यद्यपि यह कोड में dW के समान नहीं है (क्योंकि यह रीमैन योग का एक असतत कदम है), हम गणना की आसानी के लिए इसे इस तरह से मान सकते हैं। ध्यान रखें कि असतत चरणों का उपयोग हमेशा हमें एक अनुमानित राशि देगा, न कि अभिन्न मूल्य का। एक चौकस पाठक ध्यान देगा कि हम चरणों की संख्या बढ़ाकर रीमैन योग की सटीकता बढ़ा सकते हैं।

परावर्तन समीकरण सभी आने वाली प्रकाश दिशाओं का विकिरण समाप्‍त करता है $$$\ _ omega_i$ गोलार्द्ध से अधिक $$$\ _ ओमेगा$ उस बिंदु तक पहुँचता है $$$पी$ और परावर्तित प्रकाश की मात्रा लौटाता है $$$L_o$ दर्शक की ओर। आने वाले विकिरण प्रकाश स्रोतों से आ सकते हैं जिनके साथ हम पहले से ही परिचित हैं, या पर्यावरण के नक्शे से जो प्रत्येक आने वाली दिशा का ईआई निर्धारित करते हैं, जिसके बारे में हम IBL ट्यूटोरियल में बात करेंगे।

अब बाईं ओर केवल अज्ञात ही प्रतीक है $$$f_r$ BRDF फ़ंक्शन या दो-बीम परावर्तन फ़ंक्शन के रूप में जाना जाता है, जो सतह सामग्री के गुणों के आधार पर आने वाले विकिरण के मूल्य को मापता है (या तौलता है)।

BRDF

BRDF एक फ़ंक्शन है जो घटना प्रकाश की दिशा को स्वीकार करता है। $$$\ _ omega_i$ , प्रेक्षक को दिशा $$$\ _ omega_o$ सतह के लिए सामान्य $$$एन$ और पैरामीटर $$$एक$ , जो सतह खुरदरापन है। BRDF अनुमान लगाता है कि प्रत्येक व्यक्ति का प्रकाश पुंज कितना है $$$\ _ omega_i$ इसकी सामग्री के गुणों को ध्यान में रखते हुए, एक अपारदर्शी सतह के अंतिम प्रतिबिंबित प्रकाश में योगदान देता है। उदाहरण के लिए, यदि सतह पूरी तरह से चिकनी है (लगभग एक दर्पण की तरह), BRDF फ़ंक्शन सभी आने वाली प्रकाश किरणों के लिए 0.0 लौटेगा $$$\ _ omega_i$ बीम के समान कोण (परावर्तन के बाद) को छोड़कर $$$\ _ omega_o$ जिसके लिए फ़ंक्शन 1.0 वापस आ जाएगा।

BRDF सूक्ष्म चेहरों के पहले उल्लिखित सिद्धांत के आधार पर एक सामग्री के प्रतिबिंबित और अपवर्तक गुणों का अनुमान लगाता है। BRDF को शारीरिक रूप से प्रशंसनीय होने के लिए, ऊर्जा के संरक्षण के नियम का पालन करना चाहिए, अर्थात परावर्तित प्रकाश की कुल ऊर्जा कभी भी प्रकाश की ऊर्जा से अधिक नहीं होनी चाहिए। तकनीकी रूप से, ब्लाइन-फोंग मॉडल को एक BRDF माना जाता है $$$\ _ omega_i$ और $$$\ _ omega_o$ प्रवेश द्वार पर। हालांकि, ब्लिन-फोंग मॉडल को शारीरिक रूप से सही नहीं माना जाता है, क्योंकि यह ऊर्जा के संरक्षण के कानून के अनुपालन की गारंटी नहीं देता है। प्रकाश की सतह की प्रतिक्रिया के बारे में अनुमानित रूप से कई शारीरिक रूप से सही बीआरडीएफ हैं। हालांकि, लगभग सभी रीयल-टाइम ग्राफिक्स पाइपलाइन BRDF का उपयोग करते हैं, जिसे कुक-टॉरेंस BRDF के रूप में जाना जाता है।

कुक-टॉरेंस बीआरडीएफ में एक फैलाना और एक दर्पण भाग दोनों शामिल हैं:

$$

$$f_r = k_df_ {lambert} + k_sf_ {कुक - टोरेंस}$$

यहां $$$k_d$ - आने वाली प्रकाश ऊर्जा का अपवर्तित अंश, $$$k_s$ - परिलक्षित। BRDF के बाईं ओर समीकरण के फैलाना भाग होता है, जिसे यहाँ पर दर्शाया गया है $$$f_ {लाम्बर्ट}$ । यह तथाकथित लैम्बर्ट बिखरने वाला है। यह वैसा ही है जैसा हमने डिफ्यूज़ लाइटिंग के लिए इस्तेमाल किया था, और स्थिर है:

$$

$$f_ {लैंबर्ट} = \ frac {c} {\ pi}$$

जहाँ $$$सी$ - अल्बेडो या सतह का रंग (फैलाना सतह बनावट)। द्वारा विभाजन करें $$$\ pi$ बिखरी हुई रोशनी को सामान्य करने की आवश्यकता है, क्योंकि पहले संकेतित अभिन्न बीआरडीएफ युक्त गुणा से गुणा किया जाता है $$$\ pi$ (हम इसे IBL ट्यूटोरियल में प्राप्त करेंगे)।

आप आश्चर्यचकित हो सकते हैं कि यह लैंबर्टियन प्रकीर्णन कैसे फैलने वाली प्रकाश के लिए अभिव्यक्ति से मिलता-जुलता है, जिसका उपयोग हमने पहले किया था: सतह के रंग को स्केलर उत्पाद द्वारा सतह के सामान्य और प्रकाश की दिशा के बीच गुणा किया जाता है। स्केलर उत्पाद अभी भी मौजूद है, लेकिन हमारे पास बीआरडीएफ से जुड़ा हुआ है $$$n \ cdot \ omega_i$ अभिन्न में $$$L_o$ ।

BRDF के फैलाना भाग के लिए विभिन्न समीकरण हैं जो अधिक यथार्थवादी लगते हैं, लेकिन वे प्रदर्शन के मामले में अधिक महंगे हैं। इसके अलावा, जैसा कि महाकाव्य खेलों ने निष्कर्ष निकाला है: लैंबर्टियन प्रकीर्णन सबसे वास्तविक समय प्रतिपादन उद्देश्यों के लिए पर्याप्त है।

कुक-टॉरेंस बीआरडीएफ का दर्पण भाग थोड़ा सुधरा है और इसका वर्णन इस प्रकार है:

$$

$$f_ {कुक - torrance} = \ frac {DFG} {4 (\ omega_o \ cdot n) (\ omega_i \ cdot n)}$$

इसमें तीन कार्य होते हैं और हर में एक मानकीकरण गुणांक होता है। डी, एफ, और जी अक्षरों में से प्रत्येक एक निश्चित प्रकार के फ़ंक्शन का प्रतिनिधित्व करता है जो सतह के परावर्तक गुणों के एक निश्चित हिस्से का अनुमान लगाता है। उन्हें सामान्य वितरण फ़ंक्शन (NDF), फ्रेस्नेल समीकरण और ज्यामिति फ़ंक्शन के रूप में जाना जाता है:

• सामान्य वितरण समारोह: सतह खुरदरापन के आधार पर मध्ययुगीन वेक्टर के साथ उन्मुख सतह माइक्रोफ़ोर्स की संख्या का अनुमान लगाता है; यह मुख्य कार्य है जो सूक्ष्म चेहरों को दर्शाता है।
• ज्यामिति समारोह: सूक्ष्म चेहरे की आत्म-छायांकन संपत्ति का वर्णन करता है। जब सतह बल्कि खुरदरी होती है, तो सतह के कुछ सूक्ष्म चेहरे दूसरों को ओवरलैप कर सकते हैं, जिससे सतह से परावर्तित प्रकाश की मात्रा कम हो जाती है।
• फ्रेस्नेल समीकरण: विभिन्न कोणों पर सतह प्रतिबिंब के गुणांक का वर्णन करता है।

इन कार्यों में से प्रत्येक उनके भौतिक समकक्ष का एक अनुमान है, और उनके लिए अंतर्निहित भौतिक मॉडल के लिए अधिक सटीक सन्निकटन के उद्देश्य से विभिन्न कार्यान्वयन हैं; कुछ और अधिक यथार्थवादी परिणाम देते हैं, अन्य प्रदर्शन के मामले में अधिक प्रभावी होते हैं। एपिक गेम्स के ब्रायन कारिस ने विभिन्न प्रकार के अनुमानों पर बहुत अधिक शोध किया है, जिसके बारे में आप यहां जान सकते हैं। हम एपिक गेम्स से अवास्तविक इंजन 4 में उसी तरह के कार्यों का उपयोग करेंगे, अर्थात्: डी के लिए ट्रॉब्रिज-रेइट्ज जीजीएक्स , एफ के लिए फ्रेस्नेल- स्क्लिक सन्निकटन और जी के लिए स्मिथ के श्लिक-जीजीएक्स ।

सामान्य वितरण समारोह

सामान्य वितरण फ़ंक्शन डी सांख्यिकीय रूप से सूक्ष्म चेहरों के सापेक्ष सतह क्षेत्र का अनुमान लगाता है जो मध्य वेक्टर के साथ ठीक उन्मुख होते हैं $$$ज$ । कई एनडीएफ हैं जो कुछ खुरदरापन पैरामीटर को ध्यान में रखते हुए सूक्ष्म चेहरे के समग्र संरेखण के सांख्यिकीय अनुमान का निर्धारण करते हैं। हम एक Trowbridge-Reitz GGX के रूप में जाना जाएगा:

$$

$$NDF_ {GGXTR} (n, h, \ alpha) = \ frac {\ Alpha ^ 2} {\ pi ((n \ _ cdot h) ^ 2 (\ अल्फा ^ 2−1) +1) ^ 2}$$

यहां $$$ज$ मध्ययुगीन वेक्टर है, $$$\ अल्फा$ - सतह खुरदरापन का मूल्य। अगर हम चुनते हैं $$$ज$ सतह के लिए सामान्य और प्रकाश की दिशा के बीच के मध्य वेक्टर के रूप में, फिर खुरदरापन पैरामीटर को बदलते हुए, हम निम्नलिखित चित्र प्राप्त करते हैं:

जब खुरदरापन छोटा होता है (यानी, सतह चिकनी होती है), माध्य वेक्टर की दिशा में उन्मुख सूक्ष्म चेहरे एक छोटे दायरे में केंद्रित होते हैं। इस उच्च एकाग्रता के कारण, एनडीएफ एक बहुत उज्ज्वल स्थान देता है। एक खुरदरी सतह पर, जहाँ सूक्ष्म चेहरे अधिक यादृच्छिक दिशाओं में उन्मुख होते हैं, आप मध्ययुगीन वेक्टर की दिशा में उन्मुख सूक्ष्म चेहरे की एक बड़ी संख्या पाएंगे। $$$ज$ लेकिन एक बड़े दायरे में स्थित है, जो स्पॉट के रंग को अधिक ग्रे बनाता है।

GLSL कोड में, Trowbridge-Reitz GGX सामान्य वितरण फ़ंक्शन कुछ इस तरह दिखाई देगा:

 float DistributionGGX(vec3 N, vec3 H, float a) { float a2 = a*a; float NdotH = max(dot(N, H), 0.0); float NdotH2 = NdotH*NdotH; float nom = a2; float denom = (NdotH2 * (a2 - 1.0) + 1.0); denom = PI * denom * denom; return nom / denom; } 

ज्यामिति समारोह

ज्यामिति फ़ंक्शन सांख्यिकीय रूप से सापेक्ष सतह क्षेत्र का अनुमान लगाता है, जहां इसकी सूक्ष्म अनियमितता ओवरलैप होती है, जो प्रकाश किरणों को घुसने से रोकती है।

एनडीएफ के मामले में, ज्यामिति फ़ंक्शन एक इनपुट के रूप में सतह खुरदरापन गुणांक को स्वीकार करता है, जो इस मामले में निम्नलिखित का मतलब है: खुरदरी सतहों में सूक्ष्म-चेहरों के छायांकन की उच्च संभावना होगी। ज्यामिति फ़ंक्शन जो हम उपयोग करेंगे, वह GGX और Schlick-Beckmann सन्निकटन का एक संयोजन है, और इसे Schlick-GGX के रूप में जाना जाता है:

$$

$$G_ {SchlickGGX} (n, v, k) = \ frac {n \ _ cdot v} {{(n \ _ cdot v) (1 - k) + k}$$

यहां $$$k$ एक नया स्वरूप है $$$\ अल्फा$ इस पर निर्भर करते हुए कि हम प्रत्यक्ष प्रकाश व्यवस्था या IBL प्रकाश व्यवस्था के लिए ज्यामिति समारोह का उपयोग करते हैं:

$$

$$k_ {प्रत्यक्ष} = \ frac {(अल्फा + 1) ^ 2} {8}$$

$$

$$k_ {IBL} = \ frac {\ अल्फा ^ 2} {2}$$

कृपया ध्यान दें कि मूल्य $$$\ अल्फा$ आपके इंजन में खुरदरापन कैसे होता है, इसके आधार पर भिन्न हो सकते हैं $$$\ अल्फा$ । निम्नलिखित पाठों में हम विस्तार से चर्चा करेंगे कि यह पुनर्मूल्यांकन कैसे और कहां प्रासंगिक है।

ज्यामिति को प्रभावी ढंग से अनुमानित करने के लिए, हमें दृश्य की दिशा (अतिव्यापी ज्यामिति) और प्रकाश की दिशा वेक्टर (ज्यामिति की आत्म-छायांकन) दोनों को ध्यान में रखना होगा। हम स्मिथ विधि का उपयोग करके दोनों मामलों पर विचार कर सकते हैं:

$$

$$G (n, v, l, k) = G_ {उप} (n, v, k) G_ {उप} (n, l, k)$$

Schlick-GGX के साथ स्मिथ विधि का उपयोग करना $$$G_ {उप}$ अलग खुरदरापन आर के साथ निम्नलिखित चित्र देता है:

ज्यामिति फ़ंक्शन [0.0, 1.0] के बीच का एक कारक है, जहां सफेद (या 1.0) का मतलब सूक्ष्म-चेहरों की छायांकन नहीं है, और काले (या 0.0) का मतलब सूक्ष्म-चेहरों की पूर्ण छायांकन है।

GLSL में, एक ज्यामिति फ़ंक्शन को निम्न कोड में परिवर्तित किया जाता है:

 float GeometrySchlickGGX(float NdotV, float k) { float nom = NdotV; float denom = NdotV * (1.0 - k) + k; return nom / denom; } float GeometrySmith(vec3 N, vec3 V, vec3 L, float k) { float NdotV = max(dot(N, V), 0.0); float NdotL = max(dot(N, L), 0.0); float ggx1 = GeometrySchlickGGX(NdotV, k); float ggx2 = GeometrySchlickGGX(NdotL, k); return ggx1 * ggx2; } 

फ्रेस्नेल समीकरण

फ्रेस्नेल समीकरण परावर्तित और अपवर्तित प्रकाश के अनुपात का वर्णन करता है, जो उस कोण पर निर्भर करता है जिस पर हम सतह को देखते हैं। जब प्रकाश किसी सतह से टकराता है, तो फ्रेस्नेल समीकरण हमें उस कोण के आधार पर परावर्तित प्रकाश का प्रतिशत देता है जिस पर हम इस सतह को देखते हैं। प्रतिबिंब के इस अनुपात और ऊर्जा के संरक्षण के नियम से, हम सीधे प्रकाश के अपवर्तित हिस्से को प्राप्त कर सकते हैं, जो शेष ऊर्जा के बराबर होगा।

प्रत्येक सतह या सामग्री में बुनियादी चिंतनशीलता का एक स्तर होता है , जो सतह को सीधे देखते हुए मनाया जाता है, लेकिन यदि आप सतह को एक कोण पर देखते हैं, तो सभी प्रतिबिंब अधिक ध्यान देने योग्य हो जाते हैं। आप अपनी स्वयं की संभवतः लकड़ी या धातु की मेज को पहले लंबवत रूप से और फिर 90 डिग्री के करीब के कोण पर देखकर स्वयं इसे सत्यापित कर सकते हैं। आप देखेंगे कि प्रतिबिंब बहुत अधिक ध्यान देने योग्य हो जाते हैं। सभी सतहों, सैद्धांतिक रूप से, 90 डिग्री के एक आदर्श कोण पर उनसे देखे जाने पर प्रकाश को पूरी तरह से प्रतिबिंबित करते हैं। इस प्रभाव को फ्रेस्नेल नाम दिया गया है और यह फ्रेज़ेल समीकरण द्वारा वर्णित है ।

Fresnel समीकरण काफी जटिल है, लेकिन, सौभाग्य से, यह Fresnel-Schlick सन्निकटन का उपयोग करके सरल बनाया जा सकता है:

$$

$$F_ {Schlick} (h, v, F_0) = F_0 + (1 - F_0) (1 c (h \ cdot v)) ^ 5$$

$$$F_0$ सतह की मूल परावर्तनता का प्रतिनिधित्व करता है, जिसे हम अपवर्तक सूचकांक या IORs (अपवर्तन के सूचकांक) नामक कुछ का उपयोग करके गणना करते हैं, और, जैसा कि आप गोलाकार की सतह पर देख सकते हैं, दृश्य क्षेत्र की सीमाओं के करीब देखने की दिशा (देखने की दिशा और मध्य के बीच का कोण) 90 ), , , :

, . , - . (), , . , ( $$$F_0$ ) ( 0 , ) -, , .

. , , :

: 0.17, , , ( ) 0.5 1.0. , “”, $$$F_0$ RGB ( ).

, metallic workflow: , (metalness), , .

: , ; , . , 0.0 1.0. - , , , . , .

$$$F_0$ , , - , , . :

 vec3 F0 = vec3(0.04); F0 = mix(F0, surfaceColor.rgb, metalness); 

, . , $$$F_0$ . 0.04 . , , , F0 . , , .

- :

 vec3 fresnelSchlick(float cosTheta, vec3 F0) { return F0 + (1.0 - F0) * pow(1.0 - cosTheta, 5.0); } 

cosTheta .

-

BRDF - :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+k_s\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

. , , F . $$$k_s$ , , $$$k_s$ । , :

$$

$$L_o(p,\omega_o)=\int\limits_\Omega(k_d\frac{c}{\pi}+\frac{DFG}{4(\omega_o\cdot n)(\omega_i \cdot n)}) L_i(p, \omega_i)n\cdot \omega_i d\omega_i$$

, PBR. , , . , , .

PBR

, PBR, , , PBR. , PBR, . , : , .

, PBR, :

: , . , . , ; .

: , , . , , .

: . , PBR-, , : .

: , . . , . PBR- , , (1.0 — ) .

AO (ambient occlusion) : AO . , , . AO , . . , 3D-.

. PBR, , . , PBR, PBR-, , , .

• Background: Physics and Math of Shading by Naty Hoffmann: , , ; PBR, must-read .
• Real shading in Unreal Engine 4 : PBR, Epic Games Unreal Engine 4. PBR, , .
• Marmoset: PBR Theory : PBR. , , , .
• Coding Labs: Physically based rendering : , PBR.
• Coding Labs: Physically Based Rendering — Cook–Torrance : BRDF -
• Wolfire Games — Physically based rendering : PBR Lukas Orsvärn.
• [SH17C] Physically Based Shading : shadertoy (: ) Krzysztof Narkowi, PBR.