कम से कम कार्रवाई का सिद्धांत। भाग २

पिछली बार हमने सबसे उल्लेखनीय भौतिक सिद्धांतों में से एक की जांच की थी - कम से कम कार्रवाई का सिद्धांत, और एक उदाहरण पर बसे कि, यह प्रतीत होता है, इसका विरोधाभास करता है। इस लेख में, हम इस सिद्धांत से अधिक विस्तार से निपटेंगे और देखेंगे कि इस उदाहरण में क्या होता है।

इस बार हमें थोड़ा और गणित की जरूरत है। हालाँकि, मैं प्राथमिक स्तर पर लेख के मुख्य भाग को फिर से सेट करने का प्रयास करूँगा। मैं थोड़ा और अधिक कठोर और जटिल बिंदुओं को उजागर करूंगा, उन्हें लेख की मूल समझ के लिए पूर्वाग्रह के बिना छोड़ दिया जा सकता है।

सीमा की स्थिति

हम सबसे सरल वस्तु से शुरू करेंगे - एक गेंद जो अंतरिक्ष में स्वतंत्र रूप से चलती है, जिस पर कोई बल कार्य नहीं करता है। इस तरह की एक गेंद, जैसा कि ज्ञात है, समान रूप से और ठीक से चलती है। सादगी के लिए, मान लीजिए कि यह धुरी के साथ चलता है $$$x$ :

इसकी गति का सही वर्णन करने के लिए, एक नियम के रूप में, प्रारंभिक शर्तें निर्दिष्ट हैं। उदाहरण के लिए, यह निर्दिष्ट किया जाता है कि समय के प्रारंभिक क्षण में $$$t_A$ गेंद एक बिंदु पर थी $$$ए$ समन्वय के साथ $$$x_A$ और गति थी $$$v_A$ । इस रूप में प्रारंभिक शर्तें निर्धारित करने के बाद, हम विशिष्ट रूप से गेंद के आगे की गति को निर्धारित करते हैं - यह एक स्थिर गति से आगे बढ़ेगा, और समय पर इसकी स्थिति $$$टी$ प्रारंभिक स्थिति के बराबर होगा और गति बीते समय से कई गुना अधिक होगी: $$$x (t) = x_A + v_A \ cdot (t-t_A)$ । प्रारंभिक स्थितियों को सेट करने का यह तरीका बहुत स्वाभाविक और सहज ज्ञान युक्त है। हमने शुरुआती समय में गेंद की गति के बारे में सभी आवश्यक जानकारी पूछी, और फिर इसकी गति न्यूटन के नियमों द्वारा निर्धारित की जाती है।

हालांकि, यह गेंद की गति को निर्दिष्ट करने का एकमात्र तरीका नहीं है। एक और वैकल्पिक तरीका समय में दो अलग-अलग बिंदुओं पर गेंद की स्थिति निर्धारित करना है। $$$t_A$ और $$$t_B$ । यानी पूछो कि:

1) समय पर $$$t_A$ गेंद एक बिंदु पर थी $$$ए$ (समन्वय के साथ $$$x_A$ );
2) समय पर $$$t_B$ गेंद एक बिंदु पर थी $$$ब$ (समन्वय के साथ $$$x_B$ )।

अभिव्यक्ति "एक बिंदु पर थी $$$ए$ "इसका मतलब यह नहीं है कि गेंद एक बिंदु पर टिकी हुई थी $$$ए$ । समय पर $$$t_A$ वह एक बिंदु पर उड़ सकता है $$$ए$ । इसका मतलब है कि समय पर उसकी स्थिति $$$t_A$ एक डॉट के साथ मेल खाता है $$$ए$ । यही बात बिंदु पर लागू होती है $$$ब$ ।

ये दो स्थितियां भी गेंद की गति को विशिष्ट रूप से निर्धारित करती हैं। इसकी गति की गणना करना आसान है। दोनों स्थितियों को पूरा करने के लिए, गेंद की गति स्पष्ट रूप से होनी चाहिए $$$(x_B-x_A) / (t_B-t_A)$ । समय पर गेंद की स्थिति $$$टी$ फिर से प्रारंभिक स्थिति के बराबर होगा और गति बीते समय से कई गुना अधिक होगी:

$$

$$x (t) = x_A + ((x_B-x_A) / (t_B-t_A)) \ cdot (t-t_A)$$

ध्यान दें कि समस्या की स्थितियों में हमें प्रारंभिक गति निर्धारित करने की आवश्यकता नहीं थी। यह विशिष्ट रूप से शर्तों 1) और 2) से निर्धारित होता है।

दूसरे तरीके से सेटिंग करना असामान्य लगता है। शायद यह स्पष्ट नहीं है कि सामान्य रूप से उन्हें इस रूप में पूछना क्यों आवश्यक हो सकता है। हालांकि, कम से कम कार्रवाई के सिद्धांत में, यह फार्म 1) और 2) में ठीक वही स्थितियां हैं, जिनका उपयोग किया जाता है, और प्रारंभिक स्थिति और प्रारंभिक गति निर्धारित करने के रूप में नहीं।

कम से कम कार्रवाई प्रक्षेपवक्र

अब गेंद के वास्तविक मुक्त संचलन से थोड़ा सा हटा दें और निम्नलिखित विशुद्ध गणितीय समस्या पर विचार करें। मान लीजिए कि हमारे पास एक गेंद है जिसे हम किसी भी तरह से मैन्युअल रूप से स्थानांतरित कर सकते हैं। इस मामले में, हमें 1) और 2 की शर्तों को पूरा करना होगा। यानी बीच में $$$t_A$ और $$$t_B$ हमें इसे बिंदु से आगे बढ़ाना होगा $$$ए$ इस बिंदु पर $$$ब$ । यह पूरी तरह से अलग तरीकों से किया जा सकता है। ऐसी प्रत्येक विधि को गेंद का प्रक्षेपवक्र कहा जाएगा और यह समय पर गेंद की स्थिति के कार्य द्वारा वर्णित किया जा सकता है $$$x (t)$ । आइए हम समय पर गेंद की स्थिति की निर्भरता के ग्राफ पर ऐसे कई प्रक्षेपों को स्थगित करें:

उदाहरण के लिए, हम समान गति से गेंद को समान गति से आगे बढ़ा सकते हैं $$$(x_B-x_A) / (t_B-t_A)$ (हरा पथ)। या हम इसे आधे बिंदु पर रख सकते हैं $$$ए$ और फिर बिंदु पर जाने के लिए दोहरी गति $$$ब$ (नीला प्रक्षेपवक्र)। आप पहले इसे विपरीत दिशा में ले जा सकते हैं। $$$ब$ पक्ष और फिर पहले से ही स्थानांतरित करने के लिए $$$ब$ (ब्राउन प्रक्षेपवक्र)। आप इसे आगे और पीछे (लाल प्रक्षेपवक्र) में स्थानांतरित कर सकते हैं। सामान्य तौर पर, आप इसे अपनी इच्छानुसार स्थानांतरित कर सकते हैं, यदि केवल स्थितियां 1) और 2) देखी जाती हैं।

ऐसे प्रत्येक प्रक्षेपवक्र के लिए हम एक संख्या का मिलान कर सकते हैं। हमारे उदाहरण में, गेंद पर अभिनय करने वाले किसी भी बल की अनुपस्थिति में, यह संख्या बीच में अंतराल में अपने आंदोलन के पूरे समय के लिए कुल संचित गतिज ऊर्जा के बराबर है $$$t_A$ और $$$t_B$ और एक क्रिया कहलाती है।

इस मामले में, "संचित" गतिज ऊर्जा शब्द का सही अर्थ नहीं बताती है। वास्तव में, गतिज ऊर्जा कहीं भी जमा नहीं होती है, संचय का उपयोग केवल प्रक्षेपवक्र के लिए कार्रवाई की गणना करने के लिए किया जाता है। गणित में, इस तरह के संचय के लिए एक बहुत अच्छी अवधारणा है - अभिन्न:

$$

$$S = \ int \ limit_ {t_A} ^ {t_B} Tdt$$

कार्रवाई आमतौर पर पत्र द्वारा इंगित की जाती है $$$एस$ । प्रतीक $$$T$ काइनेटिक ऊर्जा का अर्थ है। इस अभिन्न का अर्थ है कि यह क्रिया गेंद की संचित गतिज ऊर्जा के बराबर होती है, जो कुछ समय के लिए होती है $$$t_A$ को $$$t_B$ ।

एक उदाहरण के रूप में, चलो 1 किलो वजन वाली गेंद लें। कुछ सीमाएं निर्धारित करें और दो अलग-अलग प्रक्षेपवक्रों के लिए कार्रवाई की गणना करें। बात करने दो $$$ब$ बिंदु से 1 मीटर है $$$ए$ और समय $$$t_B$ समय से दूर $$$t_A$ 1 सेकंड के लिए। यानी हमें उस समय गेंद को स्थानांतरित करना चाहिए जब शुरुआती समय में बिंदु पर था $$$ए$ , अक्ष के साथ 1 मीटर की दूरी पर एक सेकंड में $$$x$ ।

पहले उदाहरण (ग्रीन प्रक्षेपवक्र) में हमने गेंद को समान रूप से स्थानांतरित किया, अर्थात। समान गति के साथ, जो, स्पष्ट रूप से, समान होना चाहिए: $$$v = 1$ एम / एस समय के प्रत्येक क्षण में गेंद की गतिज ऊर्जा बराबर होती है: $$$T = mv ^ 2/2$ = 1/2 जे। एक सेकंड में, 1/2 जे जमा होगा $$$\ _ काड$ गतिज ऊर्जा के साथ। यानी ऐसे प्रक्षेपवक्र के लिए मान्य है: $$$S = 1/2$ जे $$$\ _ काड$ एक।

अब चलो तुरंत बिंदु से गेंद को स्थानांतरित न करें $$$ए$ इस बिंदु पर $$$को$ , और इसे आधे सेकंड के लिए एक बिंदु पर रखें $$$ए$ , और फिर, शेष समय के लिए, हम इसे समान रूप से बिंदु पर स्थानांतरित करते हैं $$$ब$ । पहले हाफ सेकंड में, गेंद आराम पर है और इसकी गतिज ऊर्जा शून्य है। इसलिए, प्रक्षेपवक्र के इस हिस्से की कार्रवाई में योगदान भी शून्य के बराबर है। दूसरी छमाही के लिए हम गेंद को दोगुनी गति से स्थानांतरित करते हैं: $$$v = 2$ एम / एस गतिज ऊर्जा के बराबर होगा $$$T = mv ^ 2/2$ = 2 जे। इस समय की कार्रवाई में योगदान 2 जे को आधा सेकंड से गुणा किया जाएगा, अर्थात। 1 जे $$$\ _ काड$ एक। इसलिए, इस तरह के प्रक्षेपवक्र के लिए सामान्य कार्रवाई के बराबर है $$$S = 1$ जे $$$\ _ काड$ एक।

इसी तरह, निर्दिष्ट सीमा शर्तों 1) और 2 के साथ किसी भी अन्य प्रक्षेपवक्र किसी दिए गए प्रक्षेपवक्र के लिए कार्रवाई के बराबर एक निश्चित संख्या से मेल खाती है। ऐसे सभी प्रक्षेपवक्रों में, एक प्रक्षेपवक्र होता है जिसमें क्रिया सबसे कम होती है। यह साबित किया जा सकता है कि यह प्रक्षेपवक्र एक हरा प्रक्षेपवक्र है, अर्थात गेंद की समान गति। किसी भी अन्य प्रक्षेपवक्र के लिए, चाहे वह कितना भी मुश्किल हो, कार्रवाई 1/2 से अधिक होगी।

गणित में, एक निश्चित संख्या के प्रत्येक फ़ंक्शन के लिए ऐसी तुलना को कार्यात्मक कहा जाता है। अक्सर भौतिकी और गणित में, हमारे जैसे कार्य उत्पन्न होते हैं, अर्थात्। एक फ़ंक्शन खोजने के लिए जिसके लिए एक विशेष कार्यात्मक का मूल्य न्यूनतम है। उदाहरण के लिए, गणित के विकास के लिए महान ऐतिहासिक महत्व के कार्यों में से एक है बैस्टिस्टोक्रोन की समस्या। यानी एक ऐसा वक्र खोजना जिसके साथ गेंद सबसे तेजी से लुढ़के। फिर से, प्रत्येक वक्र को फ़ंक्शन h (x) द्वारा दर्शाया जा सकता है, और प्रत्येक फ़ंक्शन को एक संख्या सौंपी जा सकती है, इस मामले में गेंद रोलिंग समय। फिर, समस्या एक फ़ंक्शन को खोजने के लिए उबालती है जिसके लिए कार्यात्मक का मूल्य न्यूनतम है। गणित का क्षेत्र जो इस तरह की समस्याओं से निपटता है, उसे विभिन्नताओं का कलन कहा जाता है।

कम से कम कार्रवाई का सिद्धांत

ऊपर चर्चा किए गए उदाहरणों में, हमारे पास दो अलग-अलग तरीकों से प्राप्त दो विशेष प्रक्षेपवक्र हैं।

पहला प्रक्षेपवक्र भौतिकी के नियमों से प्राप्त किया जाता है और एक मुक्त गेंद के वास्तविक प्रक्षेपवक्र से मेल खाता है, जो किसी भी बलों से प्रभावित नहीं होता है और जिसके लिए फार्म 1) और 2 में सीमा की स्थिति दी गई है)।

दूसरी प्रक्षेपवक्र गणितीय समस्याओं से दी गई सीमा 1 और 2) के साथ एक प्रक्षेपवक्र को खोजने के लिए प्राप्त की जाती है, जिसके लिए कार्रवाई न्यूनतम है।

कम से कम कार्रवाई का सिद्धांत बताता है कि इन दो प्रक्षेपवक्रों को मेल खाना चाहिए। दूसरे शब्दों में, यदि यह ज्ञात है कि गेंद को इस तरह से स्थानांतरित किया गया था कि सीमा 1 (2) और 2) संतुष्ट थे, तो यह आवश्यक रूप से एक पथ के साथ आगे बढ़ गया, जिसके लिए उसी सीमा शर्तों के साथ किसी भी अन्य पथ की तुलना में कार्रवाई न्यूनतम है।

कोई इसे मात्र संयोग मान सकता है। ऐसी कई समस्याएं हैं जिनमें एक समान प्रक्षेपवक्र और सीधी रेखाएं दिखाई देती हैं। हालांकि, कम से कम कार्रवाई का सिद्धांत एक बहुत ही सामान्य सिद्धांत है, अन्य स्थितियों में मान्य है, उदाहरण के लिए, एक समान गुरुत्वाकर्षण क्षेत्र में गेंद के आंदोलन के लिए। ऐसा करने के लिए, आपको बस गतिज ऊर्जा को काइनेटिक और संभावित ऊर्जा के अंतर से बदलने की आवश्यकता है। इस अंतर को लैग्रैनिज या लाग्रेंज फंक्शन कहा जाता है और यह क्रिया अब कुल संचित लैग्रैजियन के बराबर हो जाती है। वास्तव में, लैगरेंज फ़ंक्शन में सिस्टम के गतिशील गुणों के बारे में सभी आवश्यक जानकारी होती है।

यदि हम एक समान गुरुत्वाकर्षण क्षेत्र में एक गेंद लॉन्च करते हैं ताकि यह एक बिंदु से गुजरे $$$ए$ समय पर $$$t_A$ और बिंदु के लिए उड़ान भरी $$$ब$ समय पर $$$t_B$ , फिर वह, न्यूटन के नियमों के अनुसार, एक पैराबोला उड़ जाएगा। यह वह पैराबोला है जो प्रक्षेपवक्र के साथ मेल खाता है जिसके लिए कार्रवाई न्यूनतम होगी।

इस प्रकार, एक संभावित क्षेत्र में चलते हुए शरीर के लिए, उदाहरण के लिए, पृथ्वी के गुरुत्वाकर्षण क्षेत्र में, लैगरेंज फ़ंक्शन इसके बराबर है: $$$L = T (v) -V (x, y, z)$ । गतिज ऊर्जा $$$T$ शरीर की गति और क्षमता पर निर्भर करता है - इसकी स्थिति पर, अर्थात्। निर्देशांक $$$x, y, z$ । विश्लेषणात्मक यांत्रिकी में, एक सिस्टम की स्थिति का निर्धारण करने वाले निर्देशांक के पूरे सेट को आमतौर पर एक अक्षर द्वारा दर्शाया जाता है $$$q$ । एक गुरुत्वाकर्षण क्षेत्र में स्वतंत्र रूप से चलती गेंद के लिए, $$$q$ निर्देशांक का मतलब है $$$x$ । $$$य$ और $$$z$ ।

मात्रा के परिवर्तन की दर को इंगित करने के लिए, भौतिकी में बहुत बार वे बस इस मात्रा को समाप्त कर देते हैं। उदाहरण के लिए $$$\ _ x$ समन्वय के परिवर्तन की दर को इंगित करता है $$$x$ , या, दूसरे शब्दों में, दिशा में शरीर की गति $$$x$ । इन सम्मेलनों का उपयोग करते हुए, विश्लेषणात्मक यांत्रिकी में हमारी गेंद की गति को दर्शाया गया है $$$\ डॉट क्यू$ । यानी $$$\ डॉट क्यू$ मतलब गति घटक $$$v_x, v_y, v_z$ ।

चूंकि लैगरेंज फ़ंक्शन गति और निर्देशांक पर निर्भर करता है, यह स्पष्ट रूप से समय पर भी निर्भर कर सकता है (स्पष्ट रूप से समय पर निर्भर करता है इसका मतलब है कि मूल्य $$$एल$ समय में विभिन्न बिंदुओं पर, अलग-अलग, एक ही गति और गेंद की स्थिति पर) तब सामान्य रूप में कार्रवाई को लिखा जाता है

$$

$$S = \ int \ limit_ {t_A} ^ {t_B} L (\ dot q, q, t) dt$$

हमेशा न्यूनतम नहीं

हालांकि, पिछले भाग के अंत में, हमने एक उदाहरण देखा जहां कम से कम कार्रवाई का सिद्धांत स्पष्ट रूप से काम नहीं करता है। ऐसा करने के लिए, हमने फिर से एक मुफ्त गेंद ली, जो किसी भी ताकत से प्रभावित नहीं है, और उसके बगल में एक वसंत की दीवार रखी।
हमने सीमा की स्थिति ऐसी निर्धारित की कि अंक $$$ए$ और $$$ब$ मैच करो। यानी और समय पर $$$t_A$ और समय पर $$$t_B$ गेंद उसी बिंदु पर होनी चाहिए $$$ए$ । संभावित प्रक्षेपवक्रों में से एक जगह पर गेंद का खड़ा होना होगा। यानी के बीच हर समय $$$t_A$ और $$$t_B$ वह एक बिंदु पर खड़ा होगा $$$ए$ । इस मामले में गतिज और संभावित ऊर्जा शून्य के बराबर होगी, इसलिए इस तरह के प्रक्षेपवक्र के लिए कार्रवाई भी शून्य के बराबर होगी।

कड़ाई से बोलते हुए, संभावित ऊर्जा को शून्य के बराबर नहीं लिया जा सकता है, लेकिन किसी भी संख्या के लिए, क्योंकि अंतरिक्ष में विभिन्न बिंदुओं पर संभावित ऊर्जा में अंतर महत्वपूर्ण है। हालांकि, संभावित ऊर्जा के मूल्य में बदलाव न्यूनतम कार्रवाई के साथ प्रक्षेपवक्र की खोज को प्रभावित नहीं करता है। यह सिर्फ इतना है कि सभी प्रक्षेपवक्रों के लिए कार्रवाई का मूल्य एक ही नंबर से बदल जाएगा, और न्यूनतम कार्रवाई वाला प्रक्षेपवक्र न्यूनतम कार्रवाई के साथ प्रक्षेपवक्र बना रहेगा। सुविधा के लिए, हमारी गेंद के लिए हम शून्य के बराबर संभावित ऊर्जा का चयन करेंगे।

एक ही सीमा स्थितियों के साथ एक और संभावित भौतिक प्रक्षेपवक्र एक प्रक्षेपवक्र होगा जिसमें गेंद पहले दाईं ओर उड़ती है, एक बिंदु से गुजरती है $$$ए$ समय पर $$$t_A$ । फिर वह वसंत से टकराता है, इसे संकुचित करता है, वसंत, सीधा, गेंद को पीछे धकेलता है, और फिर वह इस बिंदु पर उड़ जाता है $$$ए$ । आप गेंद की गति का चयन कर सकते हैं ताकि दीवार से उछलकर, एक बिंदु उड़ जाए $$$ए$ फिलहाल सही है $$$t_B$ । इस प्रक्षेपवक्र के साथ कार्रवाई मूल रूप से बिंदु के बीच उड़ान के दौरान संचित गतिज ऊर्जा के बराबर होगी $$$ए$ और दीवार और वापस। समय की एक निश्चित अवधि होगी जब गेंद वसंत को संकुचित करती है और इसकी संभावित ऊर्जा बढ़ जाती है, और इस अवधि के दौरान संभावित ऊर्जा कार्रवाई में नकारात्मक योगदान देगी। लेकिन इस तरह की अवधि बहुत बड़ी नहीं होगी और कार्रवाई बहुत कम नहीं होगी।



यह आंकड़ा गेंद के शारीरिक रूप से संभव प्रक्षेपवक्र दोनों को दर्शाता है। हरे रंग का रास्ता आराम से एक गेंद से मेल खाता है, जबकि नीले रंग की गेंद वसंत की दीवार से उछलती है।

हालांकि, उनमें से केवल एक का न्यूनतम प्रभाव होता है, अर्थात् पहला! दूसरे प्रक्षेपवक्र में अधिक कार्रवाई होती है। यह पता चला है कि इस समस्या में दो शारीरिक रूप से संभव प्रक्षेपवक्र हैं और केवल एक न्यूनतम कार्रवाई के साथ है। यानी इस मामले में, कम से कम कार्रवाई का सिद्धांत काम नहीं करता है।

स्थिर बिंदु

यह समझने के लिए कि यहाँ क्या मामला है, चलो अब के लिए कम से कम कार्रवाई के सिद्धांत से हटते हैं और सामान्य कार्य करते हैं। चलो कुछ फंक्शन लेते हैं $$$y (x)$ और उसका कार्यक्रम बनाएं:

ग्राफ पर, मैंने हरे रंग में चार विशेष बिंदुओं को चिह्नित किया। इन बिंदुओं के लिए क्या आम है? कल्पना करें कि एक फ़ंक्शन ग्राफ़ एक वास्तविक स्लाइड है, जिस पर एक गेंद रोल कर सकती है। चार चिह्नित बिंदु इसमें विशेष हैं कि यदि आप इस बिंदु पर गेंद को स्थापित करते हैं, तो यह कहीं भी रोल नहीं करेगा। अन्य सभी बिंदुओं पर, उदाहरण के लिए, बिंदु ई, वह जगह में नहीं रह पाएगा और नीचे स्लाइड करना शुरू कर देगा। ऐसे बिंदुओं को स्थिर कहा जाता है। इस तरह के बिंदुओं को खोजना एक उपयोगी कार्य है, क्योंकि फ़ंक्शन के किसी भी अधिकतम या न्यूनतम, अगर इसमें तेज किंक नहीं हैं, तो एक स्थिर बिंदु होना चाहिए।

यदि हम इन बिंदुओं को अधिक सटीक रूप से वर्गीकृत करते हैं, तो बिंदु A फ़ंक्शन का पूर्ण न्यूनतम है, अर्थात। इसका मान किसी अन्य फ़ंक्शन मान से कम है। बिंदु B - न तो अधिकतम और न ही न्यूनतम है और इसे एक काठी बिंदु कहा जाता है। प्वाइंट सी को स्थानीय अधिकतम कहा जाता है, अर्थात फ़ंक्शन के पड़ोसी बिंदुओं की तुलना में इसमें मान अधिक है। और बिंदु D एक स्थानीय न्यूनतम है, अर्थात फ़ंक्शन के पड़ोसी बिंदुओं की तुलना में इसमें मान कम है।

ऐसे बिंदुओं की खोज गणित की एक शाखा द्वारा की जाती है जिसे गणितीय विश्लेषण कहा जाता है। एक अन्य तरीके से, इसे कभी-कभी इन्फिनिटिसिमल का विश्लेषण कहा जाता है, क्योंकि यह जानता है कि कैसे असीम मात्रा के साथ काम करना है। गणितीय विश्लेषण के दृष्टिकोण से, स्थिर बिंदुओं में एक विशेष गुण होता है, जिसके लिए वे पाए जाते हैं। यह समझने के लिए कि यह संपत्ति क्या है, हमें यह समझने की जरूरत है कि इन बिंदुओं से बहुत छोटी दूरी पर फ़ंक्शन कैसा दिखता है। ऐसा करने के लिए, हम एक माइक्रोस्कोप लेते हैं और इसे हमारे बिंदुओं पर देखते हैं। आंकड़ा दिखाता है कि विभिन्न आवर्धन पर विभिन्न बिंदुओं के आसपास के क्षेत्र में फ़ंक्शन क्या दिखता है।

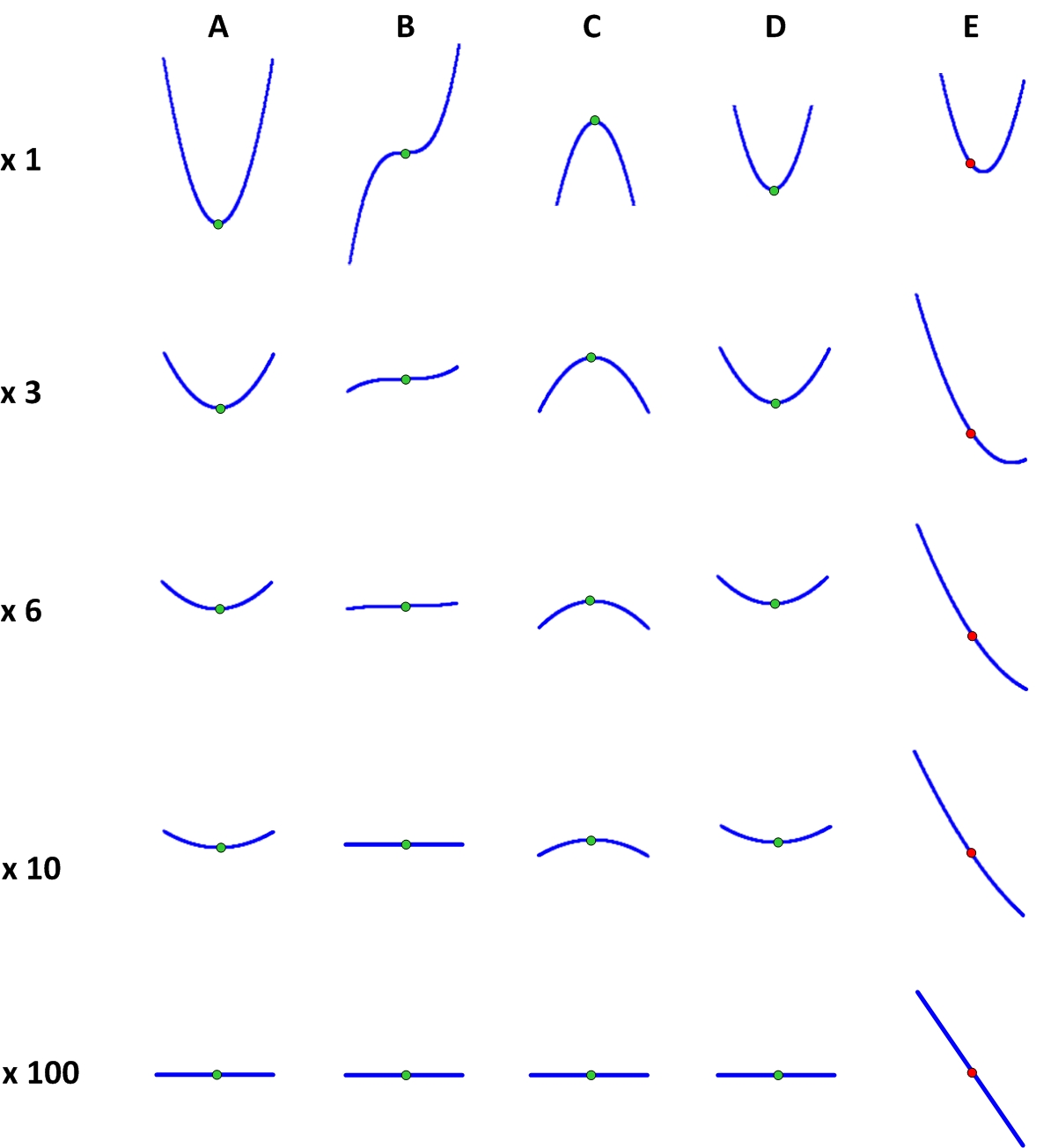
यह देखा जा सकता है कि बहुत बड़े आवर्धन पर (यानी, बहुत छोटे विचलन x पर), स्थिर बिंदु बिल्कुल समान दिखते हैं और गैर-स्थिर बिंदु से बहुत भिन्न होते हैं। यह समझना आसान है कि यह अंतर क्या है: बढ़ते हुए एक स्थिर बिंदु पर फ़ंक्शन का ग्राफ एक सख्ती से क्षैतिज रेखा बन जाता है, और गैर-स्थिर एक में यह एक झुकाव रेखा बन जाती है। यही कारण है कि एक स्थिर बिंदु पर घुड़सवार एक गेंद रोल नहीं होगी।

स्थिर बिंदु पर फ़ंक्शन की क्षैतिजता को अलग तरीके से व्यक्त किया जा सकता है: स्टेशनरी बिंदु पर फ़ंक्शन व्यावहारिक रूप से अपने तर्क में बहुत कम बदलाव के साथ नहीं बदलता है $$$x$ , यहां तक ​​कि तर्क की तुलना में। समारोह एक छोटे से बदलाव के साथ एक गैर-स्थिर बिंदु पर है $$$x$ के अनुपात में बदलता रहता है $$$x$ । और फंक्शन का एंगल जितना बड़ा होगा, फंक्शन बदलते वक्त फंक्शन उतना ही मजबूत होता है $$$x$ । वास्तव में, बढ़ते आकार के साथ कार्य विचाराधीन बिंदु पर ग्राफ़ के स्पर्शरेखा के समान अधिक से अधिक हो जाता है।

सख्त गणितीय भाषा में, "फ़ंक्शन व्यावहारिक रूप से एक बिंदु पर नहीं बदलता है $$$x_0$ बहुत कम बदलाव के साथ $$$x$ "का अर्थ है कि फ़ंक्शन के परिवर्तन और उसके तर्क के परिवर्तन का अनुपात $$$$y / Δx$ 0 पर जाता है $$$$x$ 0 से रुझान:

$$$$ $ $ $ \ lim_ {Δx \ _ 0} \ frac {(y (x_0)} {\x} = \ lim_ {x \ _ 0} \ frac {y (x_0 + Δx -y) (x_0) प्रदर्शित करें } {$x} = 0 $ $ $ $ प्रदर्शित

एक गैर-स्थिर बिंदु के लिए, यह अनुपात एक नॉनज़ेरो संख्या में जाता है, जो इस बिंदु पर फ़ंक्शन के ढलान के बराबर है। उसी संख्या को किसी दिए गए बिंदु पर फ़ंक्शन का व्युत्पन्न कहा जाता है। फ़ंक्शन के व्युत्पन्न से पता चलता है कि किसी दिए गए बिंदु के पास फ़ंक्शन अपने तर्क में एक छोटे से बदलाव के साथ कितनी तेज़ी से बदलता है $$$x$ । इस प्रकार, स्थिर बिंदु वे बिंदु हैं जिन पर फ़ंक्शन का व्युत्पन्न 0 है।

स्थिर प्रक्षेपवक्र

स्थिर बिंदुओं के साथ समानता से, स्थिर प्रक्षेपवक्र की अवधारणा को पेश किया जा सकता है। याद रखें कि प्रत्येक प्रक्षेपवक्र एक निश्चित कार्रवाई मूल्य से मेल खाता है, अर्थात्। कुछ संख्या। फिर एक ऐसा प्रक्षेपवक्र हो सकता है, जो एक ही सीमा स्थितियों के साथ इसके निकटवर्ती प्रक्षेपवक्रों के लिए, स्थिर कार्रवाई मान व्यावहारिक रूप से स्थिर प्रक्षेपवक्र के लिए कार्रवाई से अलग नहीं होगा। इस तरह के प्रक्षेपवक्र को स्थिर कहा जाता है। दूसरे शब्दों में, स्थिर के करीब किसी भी प्रक्षेपवक्र में एक एक्शन वैल्यू होगा जो इस स्थिर प्रक्षेपवक्र के लिए कार्रवाई से बहुत कम भिन्न होता है।

फिर से, गणितीय भाषा में "थोड़ा अलग" का निम्नलिखित सटीक अर्थ है। मान लीजिए कि हमारे पास एक कार्य है $$$S (x (t))$ आवश्यक सीमाओं की शर्तों 1) और 2) के साथ कार्यों के लिए, अर्थात्। $$$x (t_A) = A$ और $$$x (t_B) = B$ । मान लें कि प्रक्षेपवक्र $$$x (t)$ - स्थिर।

हम कोई अन्य फंक्शन ले सकते हैं। $$$जी (टी)$ ऐसा है कि अंत में यह शून्य मान लेता है, अर्थात $$$g (t_A)$ = $$$g (t_B)$ = 0. इसके अलावा चर ले $$$ε$ जो हम कम और कम करेंगे। इन दो कार्यों और चर का $$$ε$ हम एक तीसरा कार्य कर सकते हैं $$$x '(t) = x (t) + tg (t)$ , $$$f'(t_A)=A$ और $$$f'(t_B)=B$ । $$$ε$ , $$$x'(t)$ , $$$x(t)$ ।

$$$ε$ $$$x'(t)$ $$$x(t)$ $$$ε$ । यानी

$$

$$\lim_{ε \to 0} \frac {S(x'(t))-S(x(t))}ε=\lim_{ε \to 0} \frac {S(x(t)+εg(t))-S(x(t))}ε = 0$$

$$$g(t)$ , $$$g(t_A)$ = $$$g(t_B)$ = 0.

(, , ) $$$δS$ । «» « ».

$$$δS=0$ ।

स्थिर कार्यों को खोजने की विधि (न केवल कम से कम कार्रवाई के सिद्धांत के लिए, बल्कि कई अन्य समस्याओं के लिए भी) दो गणितज्ञों - यूलर और लाग्रेंज द्वारा पाई गई थी। यह पता चला है कि स्थिर कार्य, जिसका कार्यात्मक एक अभिन्न अभिन्न अंग के समान व्यक्त किया गया है, को एक निश्चित समीकरण को पूरा करना चाहिए, जिसे अब यूलर-लाग्रेंज समीकरण कहा जाता है।

स्थिर सिद्धांत

प्रक्षेपवक्रों के लिए न्यूनतम कार्रवाई वाली स्थिति कार्यों के लिए न्यूनतम स्थिति के समान है। प्रक्षेपवक्र के कम से कम प्रभाव के लिए, यह एक स्थिर प्रक्षेपवक्र होना चाहिए। हालांकि, सभी स्थिर प्रक्षेपवक्र न्यूनतम कार्रवाई के साथ प्रक्षेपवक्र नहीं हैं। उदाहरण के लिए, एक स्थिर प्रक्षेपवक्र में स्थानीय स्तर पर न्यूनतम कार्रवाई हो सकती है। यानीइसकी कार्रवाई किसी भी निकटवर्ती प्रक्षेपवक्र की तुलना में कम होगी। हालांकि, कहीं दूर पर अन्य प्रक्षेप पथ हो सकते हैं जिनके लिए कार्रवाई भी कम होगी।

यह पता चला है कि वास्तविक निकाय आवश्यक रूप से कम से कम कार्रवाई के साथ प्रक्षेपवक्र के साथ आगे नहीं बढ़ सकते हैं। वे विशेष प्रक्षेपवक्रों के एक व्यापक सेट के साथ स्थानांतरित कर सकते हैं, अर्थात् स्थिर प्रक्षेपवक्र। यानीशरीर का वास्तविक प्रक्षेपवक्र हमेशा स्थिर रहेगा। इसलिए, कम से कम कार्रवाई के सिद्धांत को अधिक सही ढंग से स्थिर कार्रवाई के सिद्धांत कहा जाता है। हालांकि, स्थापित परंपरा के अनुसार, इसे अक्सर कम से कम कार्रवाई का सिद्धांत कहा जाता है, न केवल न्यूनतमता, बल्कि प्रक्षेपवक्र की स्थैतिकता भी।

अब हम गणितीय भाषा में स्थिर क्रिया के सिद्धांत को लिख सकते हैं, जैसा कि आमतौर पर पाठ्यपुस्तकों में लिखा जाता है:

$$

$$δS=δ\int\limits_{t_A}^{t_B} L(\dot q,q,t)dt = 0$$

।

यहां $$$q$सामान्यीकृत निर्देशांक हैं, अर्थात चर का एक सेट जो विशिष्ट रूप से सिस्टम की स्थिति को निर्दिष्ट करता है।
$$$\dot q$ - सामान्यीकृत निर्देशांक के परिवर्तन की दर।
$$$L(\dot q,q,t)$ - लैगरेंज फ़ंक्शन, जो सामान्यीकृत निर्देशांक, उनके वेग और संभवतः, समय पर निर्भर करता है।
$$$एस$ - एक क्रिया जो सिस्टम के विशिष्ट प्रक्षेपवक्र (यानी) पर निर्भर करती है $$$q(t)$ )।

प्रणाली के वास्तविक प्रक्षेपवक्र स्थिर हैं, अर्थात्। उनके लिए कार्रवाई का एक रूपांतर$$$δS=0$ ।

यदि हम एक गेंद और एक लोचदार दीवार के साथ उदाहरण पर लौटते हैं, तो इस स्थिति का स्पष्टीकरण अब बहुत सरल हो जाता है। सीमा की स्थिति को देखते हुए कि गेंद को दौरान भी होना चाहिए$$$t_A$ और इस दौरान $$$t_B$ बात पर जाएं $$$ए$ . . , . , , . .

( ) , .