
सबसे शायद एक उचित सवाल है: क्यों?
व्यावहारिक दृष्टिकोण से कोई आवश्यकता नहीं है) आप हमेशा सशर्त टंगस्टन का उपयोग कर सकते हैं, और यदि आपको अजगर में ऐसा करने की आवश्यकता है, तो विशेष मॉड्यूल का उपयोग करें जो कि मास्टर करना इतना मुश्किल नहीं है।
लेकिन अगर आपको अचानक ऐसा काम दिया गया या आप वास्तव में प्रोग्रामिंग, मेरी तरह, तो आप रोमांचक होंगे - और कभी-कभी बहुत नहीं - एक कार्यक्रम लिखने और इसे डीबग करने के घंटे)
इस कृति को लिखते समय, हमें वास्तव में चरण-दर-चरण डिबगिंग की आवश्यकता होती है, इसलिए कृपया इस सुविधा के साथ Pyharm, VS या कुछ और डाउनलोड करें। टेबल बनाने के लिए, इस फ़ंक्शन की कमी इतनी महत्वपूर्ण नहीं है, लेकिन साजिश रचने के लिए ...
तो, मेरा कार्यक्रम क्या होगा। इनपुट में, यह तीन मान लेगा: खंड की शुरुआत और अंत जिस पर हम अपने कार्य को देखना चाहते हैं और जिस चरण के साथ हम आगे बढ़ेंगे। अगला, हम इनपुट डेटा द्वारा निर्दिष्ट मूल्यों की सीमा से प्रत्येक बिंदु पर फ़ंक्शन मानों की एक तालिका तैयार करेंगे। खैर, फिर हम चल रहे y अक्ष के साथ ही फंक्शन का ग्राफ खींचेंगे।
तो चलिए चलते हैंशुरू करने के लिए, मैं कई कार्यों की घोषणा करूंगा जिनके मूल्यों पर हम विचार करेंगे। मैं विशेष रूप से काफी सरल हूं
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x)))
अब हमारे पास तीन कार्य हैं, जिनमें से दो का विराम बिंदु है। गणित मॉड्यूल से, जो सभी गणितीय बन्स (कोसाइन, आर्कटैंट्स, और अन्य त्रिकोणमिति सहित) को संग्रहीत करता है, हम sqrt को आयात करते हैं, अर्थात वर्गमूल। फ़ंक्शन 3 को पढ़ने के लिए हमें इसकी आवश्यकता है।
उसके बाद, हमें x द्वारा फ़ंक्शन की श्रेणी और उस चरण को पढ़ने की आवश्यकता है जिसके साथ हम इस श्रेणी से गुजरते हैं। इसके लिए, मैं मानचित्र का उपयोग करूंगा।
पहले पैरामीटर के रूप में, यह फ़ंक्शन कुछ फ़ंक्शन लेता है जो किसी भी तरह से हमें आवश्यक डेटा को बदल देता है, और दूसरे तर्क के रूप में, कुछ प्रकार की डेटा शीट जिसे हमें संसाधित करने की आवश्यकता होती है
from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split())
हम एक स्थान के माध्यम से दर्ज किए गए तीन मानों को पढ़ते हैं, उन्हें एक स्थान से तत्वों में विभाजित करते हैं (विभाजन विधि का उपयोग करके, जिसे जब मापदंडों के बिना कहा जाता है, तो स्वचालित रूप से रिक्त स्थान आपके द्वारा निर्दिष्ट स्ट्रिंग को विभाजित करेगा)। इनपुट () का उपयोग करके दर्ज किया गया डेटा डिफ़ॉल्ट रूप से स्ट्रिंग, अर्थात, एक स्ट्रिंग के रूप में होगा, इसलिए हमारे यहाँ कोई त्रुटि नहीं है।
चूंकि सीमा सीमा संख्याएं भिन्नात्मक हो सकती हैं, हम परिणामस्वरूप फ़ंक्शन के प्रत्येक तत्व को फ्लोट फ़ंक्शन का उपयोग करके वास्तविक संख्या में परिवर्तित करते हैं।
ध्यान दें कि चर एक डेटा प्रकार निर्दिष्ट किए बिना घोषित किए जाते हैं। यह स्वचालित रूप से निर्धारित किया जाता है (किसी वैरिएबल को असाइन करने की कोशिश कर रहे मूल्य का डेटा प्रकार), या str, int, float, आदि कार्यों का उपयोग करना । वैरिएबल द्वारा मैन्युअल रूप से सेट किया गया है, इन समान फ़ंक्शन को मूल्यों पर लागू करना। पूरे प्रोग्राम में एक ही वैरिएबल का एक अलग डेटा टाइप हो सकता है - बस इसे एक अलग डेटा टाइप के साथ एक नया मान असाइन करें।
उदाहरण के लिए
auxiliary_variable = ""
आइये अपने कार्यक्रम पर वापस आते हैं। हमें यह जांचने की आवश्यकता है कि दर्ज किया गया डेटा सही है या नहीं।
प्रोग्राम को प्रिंट करना चाहिए कि दर्ज किया गया डेटा गलत है यदि:
- चरण ० है
- सीमा का निचला भाग ऊपरी एक से अधिक है, और चरण सकारात्मक है (अर्थात, हमारे पास xn = from_x + speed_x * (n - 1) के एक अंकगणितीय प्रगति है, जिसमें from_x> to_x । speed_x के बाद से, यह प्रगति बढ़ जाएगी और हम बढ़ जाएंगे। कभी नहीं मिल
- सीमा का निचला भाग ऊपरी एक से कम है, और चरण ऋणात्मक (समान तर्क) है
- एक बिंदु से मिलकर रेखांकन जानकारीपूर्ण नहीं है, इसलिए जिस खंड पर हम फ़ंक्शन का निर्माण करते हैं, उसमें कम से कम दो मान होने चाहिए
हम कोड में इन शर्तों को तैयार करते हैं। जाहिर है, पहला आइटम सेट करना आसान है। दूसरे और तीसरे को एक में जोड़ा जा सकता है, यदि आप ध्यान दें कि पहले (from_x) और अंतिम (to_x) के बीच अंतर का संकेत कदम के संकेत के साथ मेल खाना चाहिए। खैर, चौथा बिंदु भी इतना जटिल नहीं है: पहले और अंतिम मूल्यों के अंतर का मापांक कदम मॉड्यूल से कम नहीं होना चाहिए।
मॉड्यूल के कारण, हमारे पास एक ऐसी स्थिति हो सकती है जिसमें अंतर और चरण के संकेत मेल नहीं खाएंगे, लेकिन दूसरी स्थिति इन मामलों को काट देगी, इसलिए स्थिति सही है।
परिणामस्वरूप, ये तीन स्थितियां इस तरह दिखेंगी:
if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x):
हम सीधे मेज पर आगे बढ़ते हैं। डिबगिंग की आसानी के लिए, मैं बोलने वाले नामों के साथ कई चर बनाऊंगा जो संख्याओं की सटीकता, संख्या से पहले रिक्त स्थान की संख्या, संख्या के बाद रिक्त स्थान की संख्या आदि के लिए जिम्मेदार होंगे।
dials_precision = "%10.6g"
तो यहाँ क्या हो रहा है?

dials_precision = "%10.6g"
इस पंक्ति में मैंने संख्या की शुद्धता निर्धारित की है। पूरी संख्या के लिए अधिकतम 10 वर्ण और आंशिक भाग के लिए 6 वर्ण। यदि हमारे पास इस श्रेणी के लिए बहुत बड़ा मान है, तो सभी प्रकार के
ई -15 या कुछ समान दिखाई देंगे।
spaces_in_the_title = int((int(dials_precision[1:3])) / 2)
डायल__प्रेशन एक स्ट्रिंग है, इसलिए हम इस स्ट्रिंग का एक स्लाइस ले सकते हैं, यानी किसी प्रकार का विकल्प। इस स्थिति में, हमें संख्या 10 प्राप्त करने की आवश्यकता है, इसलिए हम 1 और 2 सूचकांकों पर वर्ण लेते हैं, हम इस विकल्प को पूर्णांक डेटा प्रकार में परिवर्तित करते हैं, दो से विभाजित करते हैं और इसे नीचे गोल करते हैं।
हमें इस चर की आवश्यकता है ताकि टेबल हेडिंग में शिलालेख सेल पर केंद्रित हों
length_of_table_lower_bound = (int(dials_precision[1:3]) + 2) * 4 + 5
जैसा कि नाम से पता चलता है, यह चर फ़ंक्शन के मानों की तालिका की कोशिकाओं की निचली सीमाओं की लंबाई के लिए जिम्मेदार है। कुल में, संख्या 10 पदों पर रहती है, जिसका अर्थ है कि कॉलम 10 से कम चौड़ा नहीं हो सकता है। जब हम ई -15 प्रारूप (ऊपर वर्णित) के साथ संख्या प्राप्त करते हैं, तो मान 11-12 स्थिति लेता है। इसलिए, 10 से हम एक और ड्यूज जोड़ते हैं।
4 स्तंभों की संख्या (x, y1, y2, y3) के लिए जिम्मेदार है, और 5 उन वर्णों की संख्या के लिए है जो एक पंक्ति में सेल को सीमित करते हैं।
शेष चर सहज ज्ञान युक्त प्रतीत होते हैं, इसलिए प्लेट को प्रिंट करने के लिए आगे बढ़ते हैं
print("|" + (spaces_in_the_title + 1) * delimiter + 'x' + spaces_in_the_title * delimiter + '|' + spaces_in_the_title * delimiter + "y1" +\ spaces_in_the_title* delimiter\ + '|' + spaces_in_the_title * delimiter + 'y2'\ + spaces_in_the_title * delimiter + '|' +\ spaces_in_the_title * delimiter\ + "y3" + spaces_in_the_title * delimiter + "|\n"\ + length_of_table_lower_bound * '-')
यदि हम अपने द्वारा लिखे गए सभी कोड को कनेक्ट करते हैं, तो कंसोल में हम इसे देखेंगे:
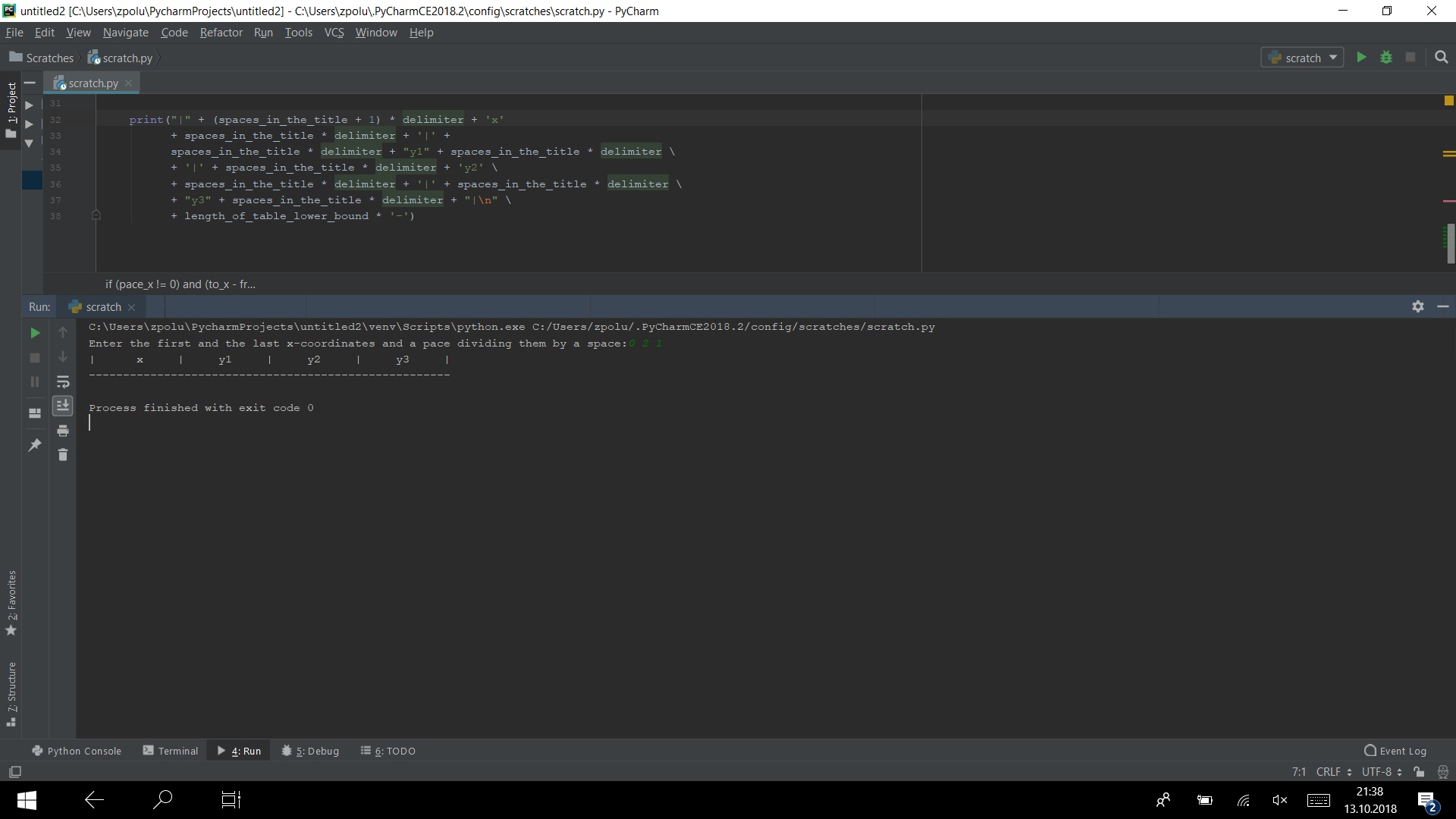
अब हमें खुद मूल्यों को छापने की जरूरत है। ऐसा करने के लिए, आपको एक लूप की आवश्यकता है। चूंकि दर्ज किया गया डेटा आंशिक हो सकता है,
रेंज का उपयोग करने से काम नहीं चलेगा, इसलिए मैं एक नियमित लूप का उपयोग करूंगा।
चूंकि हमारे पास एक्स के घटते क्रम और बढ़ते हुए दोनों हो सकते हैं, इसलिए चक्र की स्थिति निर्धारित की जानी चाहिए ताकि इन दोनों विकल्पों को ध्यान में रखा जाए। हमारे पास पहले से बना हुआ वैरिएबल है जो 0 या 1. के रूप में अनुक्रम की प्रकृति के बारे में उत्तर को संग्रहीत करता है। इसलिए, यह दो मामलों पर विचार करने और प्रत्येक के लिए उपयुक्त स्थिति का चयन करने के लिए पर्याप्त है
while(is_sequence_decreasing and x_copy >= to_x) or\ (not is_sequence_decreasing and x_copy <= to_x):
चूंकि ग्राफ के लिए हमें न्यूनतम और अधिकतम ग्राफ y1 की आवश्यकता है, जिसे हम ड्रा करेंगे, हम विशेष चर पेश करते हैं जो न्यूनतम और अधिकतम के लिए जिम्मेदार होंगे
y1_cur_value = y1(x_copy) min_y1_value = (min_y1_value > y1_cur_value) * y1_cur_value + \ (min_y1_value <= y1_cur_value) * min_y1_value max_y1_value = (max_y1_value < y1_cur_value) * y1_cur_value + \ (max_y1_value >= y1_cur_value) * max_y1_value negative_value_exists += y1_cur_value < 0
निर्माण, संक्षेप में,
यदि का निर्माण दोहराता है
: ... और: ... , केवल बूलियन असमानताओं के माध्यम से।
y1_cur_value फ़ंक्शन का वर्तमान मान संग्रहीत करता है। मैंने एक वैरिएबल बनाया है ताकि किसी फ़ंक्शन को लगातार तब न बुलाया जा सके जब एक बिंदु पर उसके मूल्य की आवश्यकता हो।
हमें साजिश रचने के लिए नकारात्मक मूल्यों की उपस्थिति की भी आवश्यकता होगी।

अब सीधे मानों को प्रिंट करें। मैं चाहता हूं कि प्रत्येक चीज सभी कोशिकाओं में सुंदर और केंद्रित हो, इसलिए मुझे संख्या की लंबाई की जांच करने के लिए प्रत्येक मूल्य को मैन्युअल रूप से संसाधित करना होगा और मूल्य संरेखित करने के लिए इसके आधार पर रिक्त स्थान की संख्या का चयन करना होगा।
टिप्पणी
वस्तुतः संख्या केन्द्रित करने से काम नहीं चलेगा। सटीकता के लिए जिम्मेदार चर में पैरामीटर जी है। उनका कहना है कि संख्याओं के लिए एक निश्चित संख्या एक संख्या के लिए आरक्षित है (हमारे मामले में, डिफ़ॉल्ट रूप से 10)। यदि 10 अंक डायल नहीं किए जाते हैं, तो रिक्त पदों को भरे गए पदों के बाईं ओर स्थित किया जाएगा। इसलिए, हम केवल 10 पदों की एक पंक्ति को केंद्र में रख सकते हैं।
aux_x = dials_precision % x_copy aux = len(aux_x) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_x) == int(dials_precision[1:3]) + 1 print('|' + delimiter * aux + aux_x + delimiter * (aux - aux_2) + '|', end='')
aux_x - एक स्ट्रिंग जो पहले से ही दिए गए सटीक के साथ एक दृश्य में लाया गया है। अब हमें संख्या की लंबाई की जांच करने और रिक्त स्थान की आवश्यक संख्या का चयन करने की आवश्यकता है। चूँकि प्रत्येक तरफ एक से अधिक स्थान की आवश्यकता नहीं होती है, फिर
बूल ईवा चर इन समान स्थानों की संख्या के संरक्षक के रूप में परिपूर्ण हैं।
aux_2 मामले को पकड़ता है जब संख्या की लंबाई 11 होती है।
हम तीन कार्यों के मूल्यों के लिए भी करते हैं
aux_y1 = dials_precision % y1_cur_value aux = len(aux_y1) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y1) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y1 + delimiter * (aux - aux_2) + '|', end='') if (x_copy != 0): aux_y2 = dials_precision % y2(x_copy) aux = len(aux_y2) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y2) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y2 + delimiter * (aux - aux_2) + '|', end='') aux_y3 = dials_precision % y3(x_copy) aux = len(aux_y3) != int(dials_precision[1:3]) + 2 aux_2 = len(aux_y3) == int(dials_precision[1:3]) + 1 print(delimiter * aux + aux_y3 + delimiter * (aux - aux_2) + \ "|\n" + length_of_table_lower_bound * '-') else: print((spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + '|' \ + (spaces_in_the_title - 2) * delimiter + " " \ + (spaces_in_the_title - 2) * delimiter + "|\n" \ + length_of_table_lower_bound * '-') x_copy += pace_x
जैसा कि मैंने पहले ही कहा था, दूसरे और तीसरे फंक्शन में ब्रेक पॉइंट होते हैं - दोनों फंक्शन पॉइंट x = 0. पर मौजूद नहीं होते हैं, इसलिए हमें इन मामलों को भी पकड़ने की जरूरत है।
खैर, वर्तमान x मान को बढ़ाने के लिए मत भूलना ताकि हमें एक अंतहीन चक्र न मिले।
चलो एक कार्यक्रम में सभी कोड इकट्ठा करते हैं और इसे चलाते हैं, उदाहरण के लिए, टेस्ट -1.2 3.6 0.3 पर
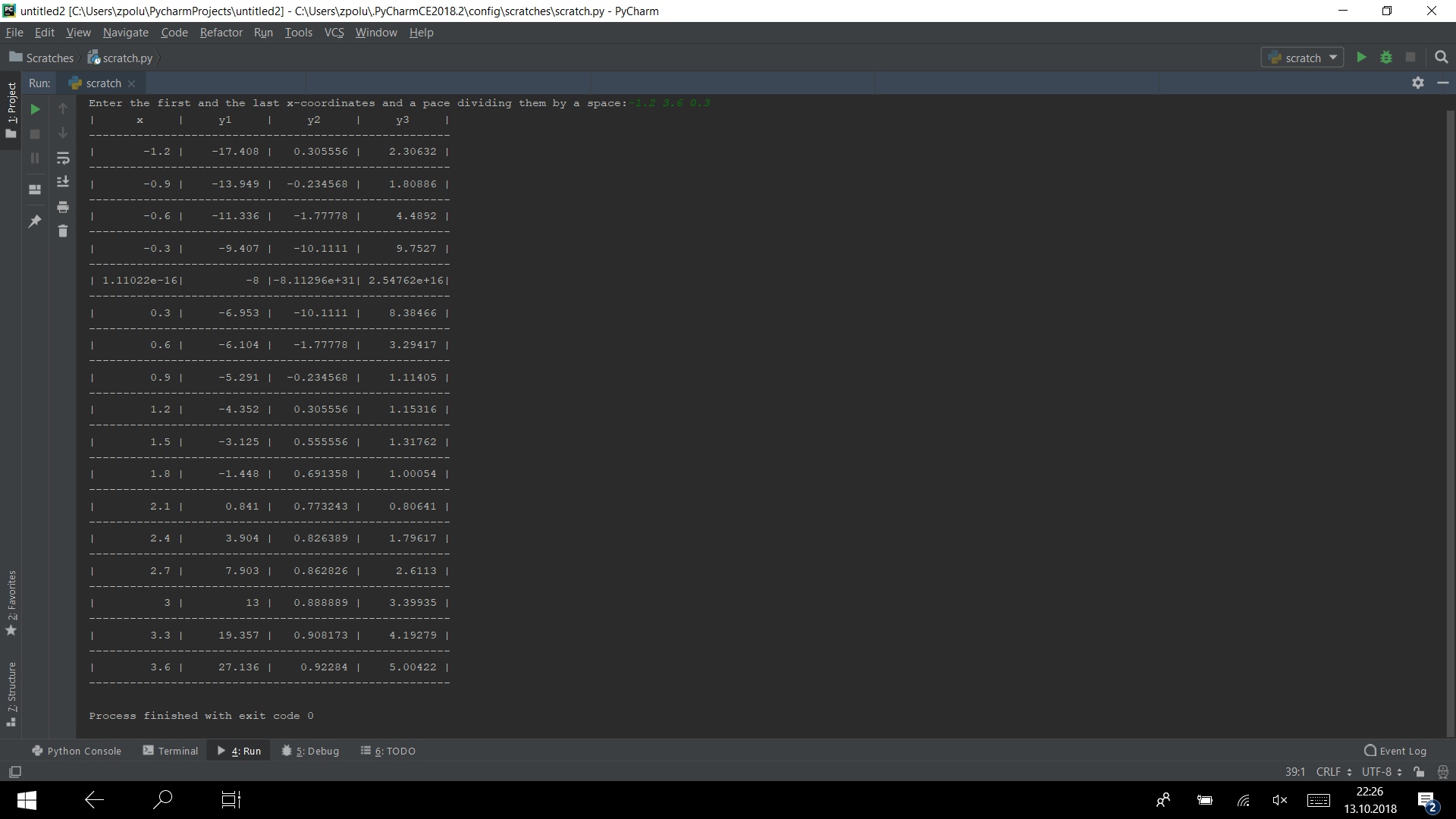
from math import sqrt def y1(x): return x**3 - 2*x**2 + 4*x - 8 def y2(x): return 1 - 1/x**2 def y3(x): return sqrt(abs(y1(x)*y2(x))) from_x, to_x, pace_x = map(float, input("Enter the first and the last"\ " x-coordinates and a pace dividing them by a"\ " space:").split()) if (pace_x != 0) and (to_x - from_x)*pace_x >= 0 and abs(to_x - from_x): dials_precision = "%10.6g"
इस निर्माण के दूसरे भाग में, हम ग्राफ़ बनाएंगे
 जारी रखने के लिए ...
जारी रखने के लिए ...