जूलिया में ग्राफिक्स। अजीब पैटर्न, एक सीधी रेखा से एक त्रिकोण का प्रतिबिंब और एक वैक्यूम में एक गोलाकार बिल्ली के मानदंडों का निर्माण

हम बहुत ही युवा, लेकिन अविश्वसनीय रूप से सुंदर और शक्तिशाली प्रोग्रामिंग भाषा जूलिया के साथ अपने परिचित को जारी रखते हैं। छह साल का बीटा आखिरकार समाप्त हो गया है, इसलिए अब आप सिंटैक्स परिवर्तनों से डर नहीं सकते। और जब हर कोई यह तर्क दे रहा है कि क्या एक से अनुक्रमण शुरू करना अच्छा है या बुरा, उत्तेजित समुदाय सक्रिय रूप से गड़बड़ कर रहा है: नए पुस्तकालय सामने आ रहे हैं, पुराने अपडेट हो रहे हैं, गंभीर परियोजनाएं शुरू हो रही हैं, और छात्र सक्रिय रूप से विश्वविद्यालयों में इस भाषा को पढ़ा रहे हैं। तो चलो पीछे नहीं रहना है! हम चाय को मजबूत बनाते हैं, क्योंकि हम इस रात को कोड करेंगे!

काम की तैयारी

यहां रूसी में एक छोटी समीक्षा है, हब पर भी भाषा और स्थापना निर्देशों के साथ एक परिचित है । फिर से, विंडोज मैनेजमेंट फ्रेमवर्क की आवश्यकता पर ध्यान केंद्रित करते हुए, पैकेज डाउनलोड करने में समस्याएं होंगी।

उन्नयन के बाद, जूलियाप्रो में अब केवल जूनो शामिल है। लेकिन मुझे व्यक्तिगत रूप से जुपिटर अधिक पसंद है: लैपटॉप पर इसके साथ कोई समस्या नहीं थी, साथ ही यह ब्राउज़र में काम करने के लिए सुविधाजनक है और तुरंत नोट्स और सूत्र तैयार करता है, सामान्य तौर पर, रिपोर्ट, स्लाइड या मैनुअल बनाने के लिए आदर्श।

जूलिया के लिए कई पैकेज हैं, उनमें से सबसे सफल बैकेंड के रूप में प्लॉट्स में शामिल हैं। Plots.jl - Plots.jl का Plots.jl : Plots.jl , विभिन्न चार्टिंग पुस्तकालयों के लिए एक इंटरफ़ेस। इस प्रकार, Plots.jl वास्तव में सिर्फ आपकी आज्ञाओं की व्याख्या करता है और फिर कुछ प्रकार के ग्राफ़ लाइब्रेरी का उपयोग करके ग्राफ़ बनाता है। इन बैकग्राउंड ग्राफिक्स लाइब्रेरी को बैकेंड कहा जाता है। सबसे अच्छी बात यह है कि आप Plots.jl सिंटैक्स के साथ कई अलग-अलग ग्राफिक्स लाइब्रेरी का उपयोग कर सकते हैं, और हम यह भी देखेंगे कि Plots.jl इनमें से प्रत्येक लाइब्रेरी में नई सुविधाएँ जोड़ता है!

 # Pkg.add("Plots") #      0.7.0 julia>] pkg>add Plots pkg>add GR pkg>add PyPlot pkg>add Gadfly pkg>add PlotlyJS pkg>add UnicodePlots 

अंतहीन प्रमुख पैटर्न

हैबर पर एक लेख के विचार को लागू किया। कुछ शब्दों में: क्या होगा यदि हम बिंदु के समन्वय को लेते हैं और एक ऑपरेशन का उपयोग करते हैं, कहते हैं, XOR या बिटवाइज़ और फ़िरस्किसा और ऑर्डिनेट के बीच, और फिर सादगी के लिए या फ़ाइबोनैचि संख्याओं से संबंधित संख्या की जाँच करें, और यदि उत्तर हाँ है, तो बिंदु को एक रंग से भरें, और दूसरे में एक नकारात्मक के साथ? की जाँच करें:

 using Plots plotlyjs() function eratosphen(n, lst) #   ar = [i for i=1:n] ar[1] = 0 for i = 1:n if ar[i] != 0 push!(lst, ar[i]) for j = i:i:n ar[j] = 0 end end end end ertsfn = [] eratosphen(1000, ertsfn) # print(ertsfn) # print( size(ertsfn) ) # -> 168 N = 80 M = 80 W1 = [in( x % y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x % y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y is prime?") p2 = spy(W2, title = "x % y") plot(p1, p2, layout=(2),legend=false) 

 W1 = [in( x + y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x + y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x + y is prime?") p2 = spy(W2, title = "x + y") plot(p1, p2, layout=(2),legend=false) 

 W1 = [in( x | y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x | y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x | y is prime?") p2 = spy(W2, title = "x | y") plot(p1, p2, layout=(2),legend=false) 

 W1 = [in( x & y, ertsfn) for x = 1:N, y = 1:M]; W2 = [x & y for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x & y is prime?") p2 = spy(W2, title = "x & y") plot(p1, p2, layout=(2),legend=false) 

 W1 = [in( xor(x, y), ertsfn) for x = 1:N, y = 1:M]; W2 = [xor(x, y) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y is prime?") p2 = spy(W2, title = "x xor y") plot(p1, p2, layout=(2),legend=false) 

 function fib(n) a = 0 b = 1 for i = 1:n a, b = b, a + b end return a end fbncc = fib.( [i for i=1:10] ) 

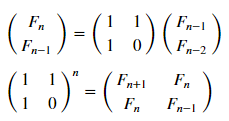
 matr_fib = n -> [1 1; 1 0]^(n-1) #  ,     n-1 mfbnc = [ matr_fib( i )[1,1] for i=1:17]; #  1,1    n-    N = 100 M = N W1 = [in( x % y, mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x | y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x % y ∈ fibonacci?") p2 = spy(W2, title = "x | y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false) 

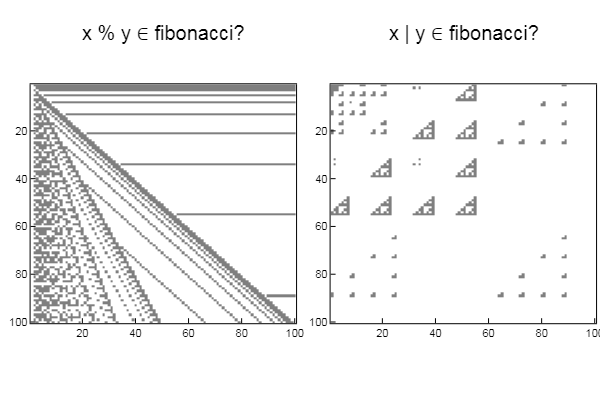
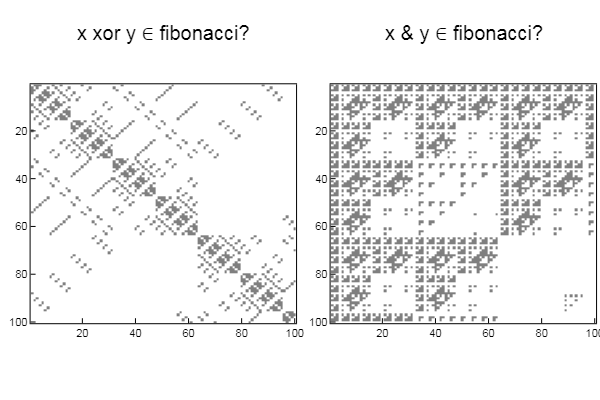
 W1 = [in( xor(x, y), mfbnc) for x = 1:N, y = 1:M]; W2 = [in( x & y, mfbnc) for x = 1:N, y = 1:M]; p1 = spy(W1, title = "x xor y ∈ fibonacci?") p2 = spy(W2, title = "x & y ∈ fibonacci?") plot(p1, p2, layout=(2),legend=false) 

अपेक्षाकृत सीधे एक आकृति का प्रतिबिंब

इस प्रकार का प्रदर्शन मैट्रिक्स द्वारा निर्धारित किया जाता है:

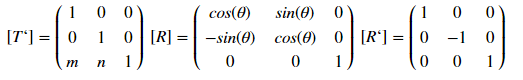
जहां [टी '], [आर] और [आर ’], क्रमशः, विस्थापन, रोटेशन और प्रतिबिंब मैट्रिक्स। यह कैसे काम करता है? आइए हम ऑफसेट के एक उदाहरण का विश्लेषण करते हैं - निर्देशांक (x, y) के साथ एक बिंदु के लिए, x द्वारा m द्वारा x और खेल द्वारा n को परिवर्तन द्वारा निर्धारित किया जाएगा:

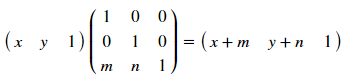
ये मैट्रीक विभिन्न बहुभुजों के लिए रूपांतरण की अनुमति देते हैं, मुख्य बात यह है कि एक दूसरे के तहत निर्देशांक रिकॉर्ड करना है और अंत में इकाई कॉलम के बारे में नहीं भूलना है। इस प्रकार [T]:

• बहुभुज के रूप में मूल में रेखा को बदल दिया जाता है
• एक्स अक्ष के साथ मेल खाने के लिए इसे घुमाता है
• एक्स के संबंध में बहुभुज के सभी बिंदुओं को दर्शाता है
• रिवर्स रोटेशन और स्थानांतरण के बाद

पुस्तक रोजर्स डी।, एडम्स जे। मैथमेटिकल फ़ाउंडेशन ऑफ़ कंप्यूटर ग्राफ़िक्स में इस विषय का अधिक विस्तार से वर्णन किया गया है

अब इसे कोड करें!

 using Plots plotlyjs() f = x -> 0.4x + 2 #    #       X = [2 4 2 2]' Y = [4 6 6 4]' xs = [-2; 7] #    ys = f(xs) inptmtrx = [ XY ones( size(X, 1), 1 ) ] #    m = 0 n = -f(0) #   Y displacement = [1 0 0; 0 1 0; mn 1] a = (ys[2]-ys[1]) / (xs[2]-xs[1]) #     θ = -atan(a) rotation = [cos(θ) sin(θ) 0; -sin(θ) cos(θ) 0; 0 0 1] reflection = [1 0 0; 0 -1 0; 0 0 1] T = displacement * rotation * reflection * rotation^(-1) * displacement^(-1) #    outptmtrx = inptmtrx * T plot( X, Y) plot!( xs, ys ) plot!( outptmtrx[:,1], outptmtrx[:,2] ) 

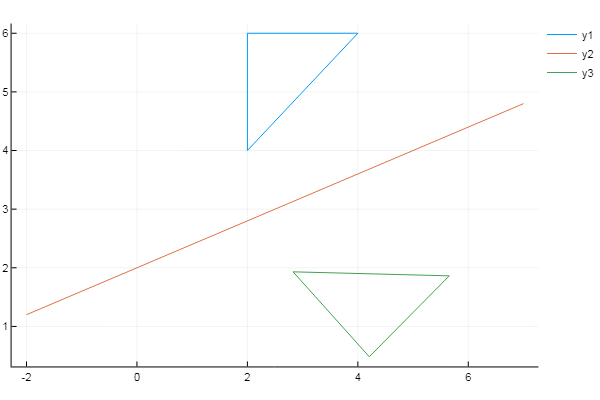
दिलचस्प तथ्य: यदि आप ग्रीक वर्णों से छुटकारा पा लेते हैं और पहली पंक्ति को बदल देते हैं

 function y=f(x,t) y=0.4*x + 2 endfunction, 

चूंकि कोष्ठक [] पर () , और plot( X, Y, xs, ys, trianglenew(:,1), trianglenew(:,2) ) पर सरणियों के अनुक्रमित को फ्रेम करते हैं, फिर यह कोड सिलाब में काफी लॉन्च किया जाता है।

त्रि-आयामी ग्राफिक्स के साथ काम करें

इनमें से कुछ पैकेज तीन-आयामी रेखांकन के निर्माण का समर्थन करते हैं। लेकिन मैं माकी के बल्कि शक्तिशाली विज़ुअलाइज़ेशन टूल का अलग से उल्लेख करना चाहूंगा, जो GLFW और GLAbstraction संकुल के साथ मिलकर काम करता है जो जूलिया में OpenGL सुविधाओं को लागू करता है। माकी के बारे में अधिक जानकारी। हम उसके अनुमोदन को छिपाते हैं

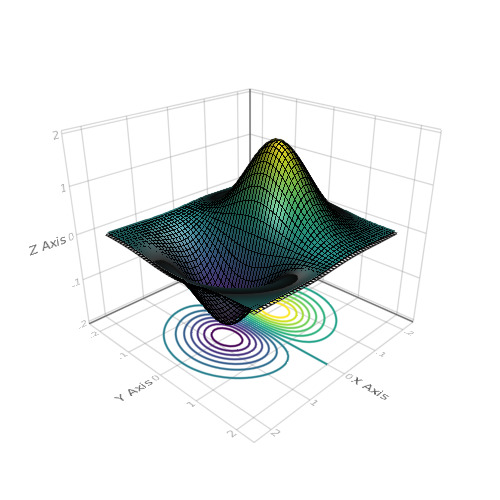
 using Makie N = 51 x = linspace(-2, 2, N) y = x z = (-x .* exp.(-x .^ 2 .- (y') .^ 2)) .* 4 scene = wireframe(x, y, z) xm, ym, zm = minimum(scene.limits[]) scene = surface!(scene, x, y, z) contour!(scene, x, y, z, levels = 15, linewidth = 2, transformation = (:xy, zm)) scene 

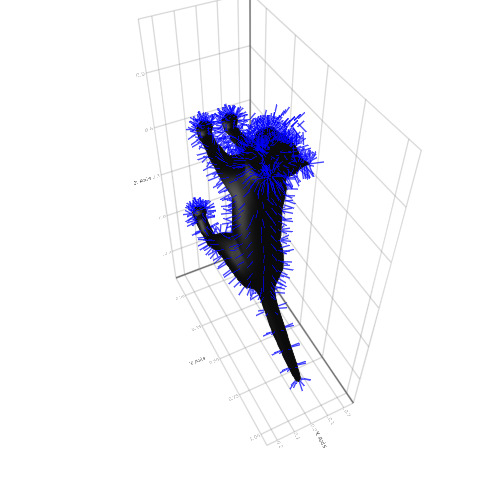
 wireframe(Makie.loadasset("cat.obj")) 

 using FileIO scene = Scene(resolution = (500, 500)) catmesh = FileIO.load(Makie.assetpath("cat.obj"), GLNormalUVMesh) mesh(catmesh, color = Makie.loadasset("diffusemap.tga")) 

 x = Makie.loadasset("cat.obj") mesh(x, color = :black) pos = map(x.vertices, x.normals) do p, n p => p .+ (normalize(n) .* 0.05f0) end linesegments!(pos, color = :blue) 

यही सब ग्राफिक्स के साथ है। अन्तरक्रियाशीलता, एनीमेशन, 3 डी, बड़े डेटा या सरल रेखांकन के तेजी से निर्माण - लगातार विकसित होने वाले पैकेज लगभग किसी भी स्वाद और जरूरतों को पूरा करेंगे, और इसके अलावा, सब कुछ सीखना बहुत आसान है। व्यावहारिक अभ्यास डाउनलोड करने के लिए स्वतंत्र महसूस करें और जूलिया को समझना जारी रखें!

UPD: उपरोक्त सभी सूचियाँ जुपिटर में जूलिया 0.6.4 के साथ बनाई गई हैं। दुर्भाग्य से, भूखंड मेटा-पैकेज के कुछ कार्यों को या तो हटा दिया गया था या नाम बदल दिया गया था, इसलिए हम अपडेट के लिए निगरानी करना जारी रखते हैं, लेकिन अभी के लिए जासूस पूरी तरह से बदल दिया गया है:

 julia> using GR julia> Z = [x | y for x = 1:40, y = 1:40]; julia> heatmap(Z)