अगर अंतरिक्ष के साथ-साथ जीआरटी प्रकाश में फैला हो तो LIGO गुरुत्वाकर्षण तरंगों को कैसे देख सकता है?

यदि दर्पण के बीच की जगह के साथ प्रकाश को फैलाएंगे तो LIGO गुरुत्वाकर्षण तरंगों का पता कैसे लगा सकता है?

छवि क्रेडिट: www.ligo.caltech.edu

यह सवाल निश्चित रूप से उठता है जब बातचीत गुरुत्वाकर्षण तरंगों (GW) का पता लगाती है। आमतौर पर तर्क इस प्रकार है: हम जानते हैं कि एक गुरुत्वाकर्षण रेडशिफ्ट है , अर्थात गुरुत्वाकर्षण तरंग दैर्ध्य को बढ़ाता है। यह मान लेना उचित है कि LIGO में प्रकाश भी खिंचेगा और तरंग दैर्ध्य जो हम दर्पण के बीच की दूरी को मापने के लिए "शासक" के रूप में उपयोग करते हैं, दूरी के समान ही खिंच जाएगा। तो गुरुत्वाकर्षण तरंगों को मापने के लिए एक इंटरफेरोमीटर का उपयोग कैसे किया जा सकता है?

इसके संभावित उत्तर की कल्पना करें:

1. जीवी प्रकाश को प्रभावित नहीं करता है, इसलिए प्रश्न का कोई मतलब नहीं है।
2. जीडब्ल्यू प्रकाश की तरंग दैर्ध्य को बढ़ाते हैं, लेकिन बहुत कमजोर रूप से, इसलिए हम ध्यान नहीं देते हैं।
3. इससे कोई फर्क नहीं पड़ता, पता लगाने का सिद्धांत तरंग दैर्ध्य के प्रति संवेदनशील नहीं है।
4. डिटेक्टर वास्तव में काम नहीं करते हैं।

1. क्या कोई लड़का था?

शुरू करने के लिए, डिटेक्टर अभी भी काम करते हैं।


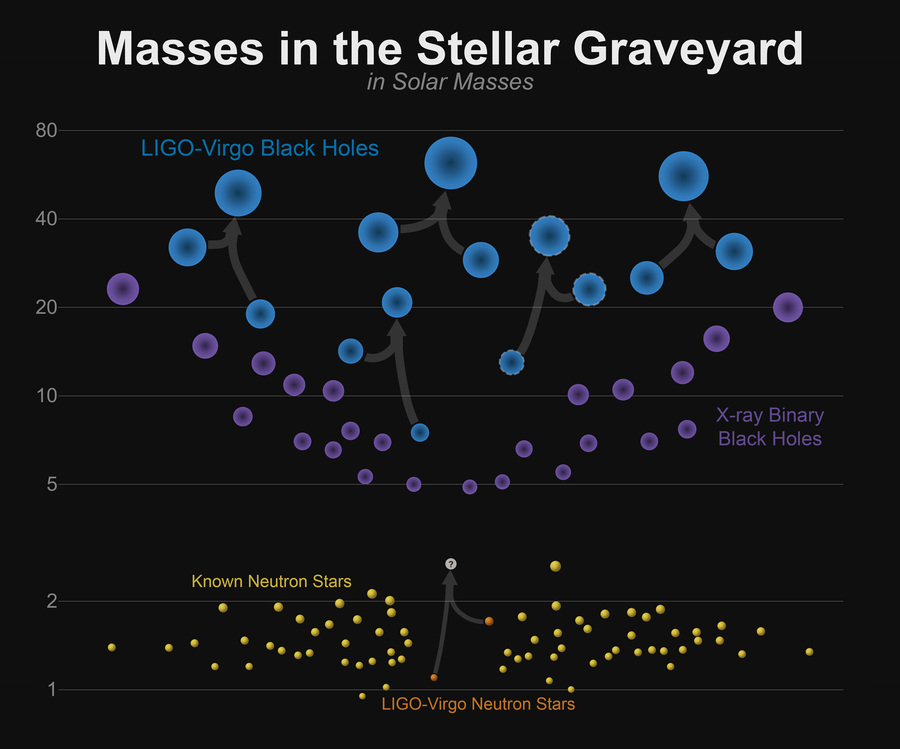तारों का कब्रिस्तान: न्यूट्रॉन सितारों का द्रव्यमान और हमारे लिए ज्ञात ब्लैक होल, जिसमें LIGO के अवलोकन भी शामिल हैं। छवि क्रेडिट: www.ligo.caltech.edu


फिलहाल, हमने जीडब्ल्यू से एक दर्जन से अधिक घटनाओं को देखा है। सबसे अधिक आश्वस्त जीडब्ल्यू का संयुक्त पता लगाने और न्यूट्रॉन सितारों के संलयन से प्रकाश की चमक है । LIGO में, उन्होंने GW को देखा, आकाश में उस क्षेत्र को त्रिभुजित किया, जहाँ से वे आते हैं, और दूरबीनों से कहा: "वहाँ देखो!" उन्होंने देखा, और ठीक उसी तरह देखा, जैसे कि LIGO से संकेत मिलता है। इसलिए इसमें कोई संदेह नहीं है कि यह काम करता है। आइए देखें कि वास्तव में कैसे।

2. सामान्य में LIGO क्या है?

कन्या डिटेक्टर एक यूरोपीय डिटेक्टर है, तीन डिटेक्टरों में से एक है जिसने गुरुत्वाकर्षण तरंगों को देखा है। छवि क्रेडिट: www.ligo.caltech.edu

एक गुरुत्वाकर्षण लहर, जो बड़े पैमाने पर वस्तुओं के विलय के दौरान उत्पन्न होती है (उदाहरण के लिए, दो ब्लैक होल), अपने वक्रता के एक छोटे से गड़बड़ी के रूप में अंतरिक्ष-समय में प्रचार करती है। यह इस तथ्य की ओर जाता है कि वस्तुओं के बीच की दूरी थोड़ी बदल जाती है जब लहर उनके बीच से गुजरती है (अधिक सटीक रूप से, दूरी में परिवर्तन की परिभाषा)। एलआईजीओ में, 4 किमी के दो हथियार माइकलसन इंटरफेरोमीटर ~ 10 ^-18 मीटर द्वारा बदलते हैं, और डिटेक्टर इस बदलाव का पता लगाने में सक्षम है। एक महत्वपूर्ण बिंदु: यदि वेवगाइड इंटरफेरोमीटर के एक हाथ को फैलाता है, तो दूसरा हाथ आनुपातिक रूप से संकुचित हो जाएगा (आदर्श रूप से, यह वेवगाइड की चौगुनी प्रकृति और दो ध्रुवीकरणों की उपस्थिति से निम्नानुसार है)।

LIGO डिवाइस के बारे में Habré पर पहले से ही एक अच्छा लेख है , तो चलिए लेख की शुरुआत में प्रस्तुत प्रश्न का उत्तर देने के लिए आगे बढ़ते हैं।

3. मापन अवधारणा

एक एनीमेशन जो दर्शाता है कि डिटेक्टर कैसे काम करता है

शुरू करने के लिए, एक उदाहरण पर विचार करें जो आपको डिटेक्टर के मूल सिद्धांत को समझने में मदद करेगा।
यह डिटेक्टर निरंतर प्रकाश के साथ काम करता है - लेजर लगातार प्रकाश के साथ LIGO में गुंजयमान यंत्र को पंप करता है, और फोटोडायोड लगातार एक संकेत की उपस्थिति / अनुपस्थिति का पता लगाता है। लेकिन उदाहरण के लिए, आइए योजना को सरल करें: मान लें कि हमारे पास एक फोटॉन स्रोत है जो एक साथ दो दिशाओं में फोटॉन भेजता है, वहां वे दर्पण से परिलक्षित होते हैं और फोटॉन डिटेक्टर (हमारे मामले में, बीम फाड़नेवाला) में वापस आ जाते हैं, जैसा कि नीचे चित्रण में दिखाया गया है।



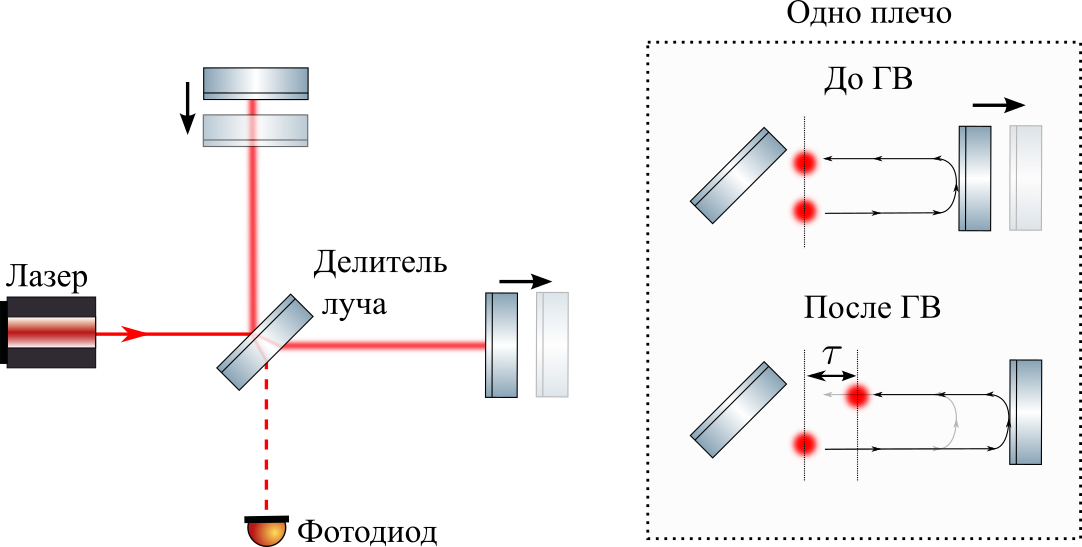
यदि दो दर्पण फोटॉन स्रोत से समान दूरी पर हैं, तो दो फोटॉनों एक ही समय में डिटेक्टर पर वापस आ जाएंगे (जैसा कि आंकड़े में है)। यदि जीडब्ल्यू एक कंधे पर फैला है $$$x$ , और दूसरे पर संपीड़ित करता है $$$x$ फिर एक फोटॉन पहले से दूसरे पर आ जाएगा $$$2 \ tau = 4x / c \ sim 4 \ गुना 10 ^ {- 18} / (3 * 10 ^ 8) \ sim 10 ^ {- 26}$ सी, जैसा कि ऊपर की आकृति में है। यह बहुत छोटा है, ज़ाहिर है, और सीधे मापना असंभव होगा, लेकिन हम थोड़ा अलग तरीके से मापते हैं। मैं इस पोस्ट का मुख्य संदेश दिखाना चाहता था:

डिटेक्टर एक शासक नहीं है, बल्कि एक घड़ी है

4. विस्तृत विवरण

आइए अब हम माइकलसन इंटरफेरोमीटर पर विचार करते हैं, जिसमें वे एक निरंतर लेजर के साथ चमकते हैं, बीम को समान रूप से बीम फाड़नेवाला द्वारा विभाजित किया जाता है, अंतिम दर्पण से परिलक्षित होता है और, बीम फाड़नेवाला पर वापस लौटता है, हस्तक्षेप करता है।



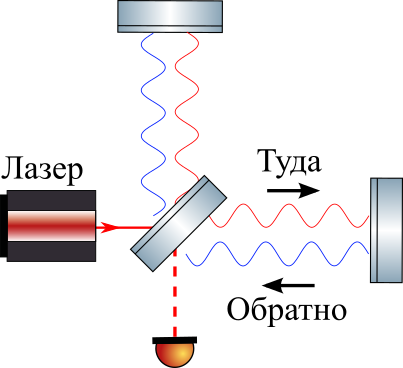
सादगी के लिए, हम मानते हैं कि GW एक "चरण" है - यह थोड़ी मात्रा में मीट्रिक को तुरंत बदल देता है $$$h_0$ । "मीट्रिक परिवर्तन" शब्दों से हमारा मतलब है कि दूरी की परिभाषा कुछ हद तक बदल जाती है, अर्थात्। सभी दूरियां बढ़ जाती हैं (या घट जाती हैं) $$$(1+ h_0 / 2)$ समय। यदि हम बीम फाड़नेवाला और अंतिम दर्पण के बीच की दूरी पर विचार करते हैं $$$एल$ , जब मीट्रिक बदलता है, तो यह बढ़ेगा $$$\ Delta L$ ताकि $$$h_0 = 2 \ Delta L / L$ ।

नोट: यह महत्वपूर्ण है कि "कदम" के रूप में GW का प्रतिनिधित्व केवल उंगलियों पर विचार के लिए उपयोगी है, वास्तव में, GW को एक निश्चित लंबाई के साथ एक लहर के रूप में मानना ​​आवश्यक है।

गौर कीजिए कि इस समय प्रकाश क्या होता है।


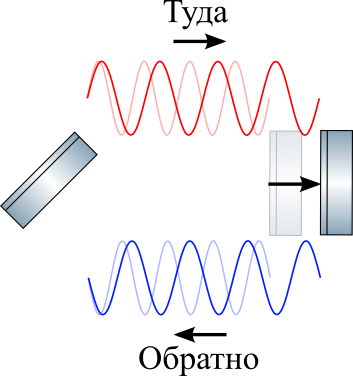GW के आगमन के समय, मूल तरंगदैर्ध्य (पारभासी वक्र) के सापेक्ष प्रकाश की तरंगदैर्ध्य खिंच जाती है। एनबी: दिखाया गया तरंग दैर्ध्य स्पष्टता के लिए कंधे की लंबाई के बराबर है, वास्तव में, लेजर तरंग दैर्ध्य लगभग 1 माइक्रोन है, और कंधे की लंबाई 4 किमी है।

यदि दर्पण में स्ट्रेचिंग से पहले एक खड़े तरंग की गाँठ होती है, तो वह स्ट्रेचिंग के बाद वहीं रहेगी, जैसा कि ऊपर चित्र में दिखाया गया है। क्यों? यह सापेक्षता के सिद्धांत द्वारा आवश्यक है: चूंकि अलग-अलग स्वतंत्र आराम प्रणाली नहीं है, नोड को कुछ भी नहीं करना है, लेकिन जहां यह दर्पण की सतह के सापेक्ष था, वहां रहने के लिए कुछ भी नहीं है। यही है, में तरंग दैर्ध्य बढ़ता है $$$(1 + h_0 / 2)$ समय, जैसा कि लेख की शुरुआत में उम्मीद की जाती है, गुरुत्वाकर्षण रेडशिफ्ट के अनुरूप है।

तो यह पता चला है कि सभी समान प्रकाश डिटेक्टर के साथ बढ़ाया गया था, और हम सिग्नल को पंजीकृत नहीं कर सकते हैं?

और फिर भी हम कर सकते हैं!



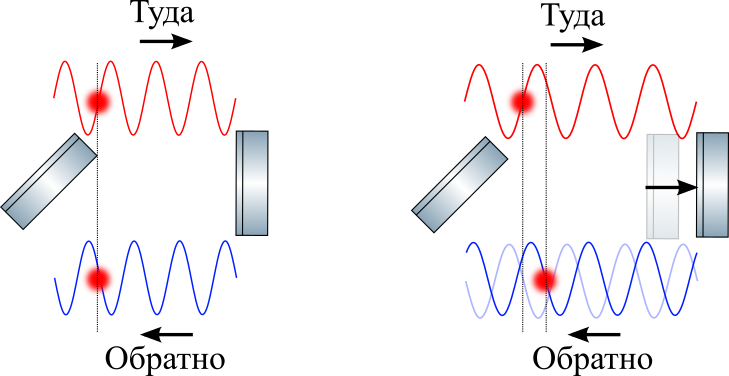
हम इसे ऊपर की तस्वीर में दिखाएंगे: हम एक विशेष नोड के रास्ते को वहां और पीछे के रास्ते पर एक खिंचाव वाली लहर में एक सर्कल के साथ चिह्नित करेंगे। स्ट्रेचिंग के बावजूद, प्रकाश अभी भी प्रकाश की गति से फैलता है। इसका मतलब यह है कि लहर के उस भाग के लिए जो अभी-अभी कंधे में घुसा है, उसे गोल यात्रा पर काबू पाने में अधिक समय लगेगा (यहां से अनुच्छेद 3 को याद करें)। यही है, आगमन पर इसका चरण बदल जाएगा (जैसा कि चित्र में देखा जा सकता है)।

इसके अलावा, एक निरंतर तरंग दैर्ध्य के साथ प्रकाश पंप करना जारी रखता है।

विभक्त से दर्पण और इसके विपरीत रास्ते पर प्रकाश द्वारा संचित चरण प्रकाश की प्राकृतिक आवृत्ति पर निर्भर करता है $$$\ _ ओमेगा _ {\ rm sob}$ किरण फाड़नेवाला और समय पर मनाया $$$\ _ ताऊ _ {\ rm गोल यात्रा}$ :

$$

$$\ phi = \ omega _ {\ rm sob} \ tau _ {\ rm गोल यात्रा}$$

यह दिखाया जा सकता है (उदाहरण के लिए, यहां या यहां ) कि अगर HW की तरंग दैर्ध्य इंटरफेरोमीटर के हाथ की लंबाई से बहुत अधिक है, तो प्राकृतिक आवृत्ति व्यावहारिक रूप से नहीं बदलती है। और देरी का समय दर्पणों के बीच की दूरी पर निर्भर करेगा:

$$

$$\ tau _ {\ rm गोल यात्रा} \ लगभग \ frac {2 L} {c} (1+ \ frac {h_0} {2})$$

तदनुसार, बीम विभक्त के आने पर, प्रकाश के चरण में देरी होगी, जो मीट्रिक के आकार पर निर्भर करता है $$$h_0$ । दूसरे कंधे में, सब कुछ वैसा ही होगा, सामने संकेत पर सटीक $$$h_0$ - क्योंकि यह कंधे फैला नहीं होगा, लेकिन संकुचित। नतीजतन, बीम फाड़नेवाला पर, दोनों कंधों के बीच चरण अंतर होगा

$$

$$\ Delta \ phi = \ frac {2 \ omega L} {c} (1+ \ frac {h_0} {2}) - \ frac {2 \ _ \ _ oomega L} {c} (1- \ frac / h_0) { 2}) = 2 \ pi \ frac {L} {\ lambda} h_0$$

इस समीकरण से, यह स्पष्ट है कि डिटेक्टर की इतनी लंबी भुजा क्यों है - तरंगदैर्घ्य की तुलना में लंबाई L जितनी अधिक होगी, उतनी ही अधिक संवेदनशील होगी। अगली पीढ़ी के डिटेक्टर, जैसे कि आइंस्टीन टेलीस्कोप या कॉस्मिक एक्सप्लोरर , 10 से 40 किमी से अधिक लंबा होगा।

मैं ध्यान देता हूं कि वास्तव में GW एक "चरण" नहीं है, यह कंधे की लंबाई की तुलना में बहुत अधिक तरंग दैर्ध्य वाली लहर है, ताकि, जबकि प्रकाश तरंग का एक "नोड" आगे और पीछे से गुजरता है, इसकी स्ट्रेचिंग की उपेक्षा की जा सकती है। इसलिए, "उंगलियों पर" विचार से प्रकाश के "खींच" का पहला क्षण वास्तव में लगभग अनुपस्थित है।

तो, निष्कर्ष। प्रश्न का सही उत्तर लेख की शुरुआत में है: 2 और 3 - गुरुत्वाकर्षण तरंगें दोनों दर्पणों के बीच की दूरी की तुलना में थोड़ी अलग तरह से प्रकाश पर काम करती हैं, लेकिन इससे कोई फर्क नहीं पड़ता, क्योंकि किसी भी मामले में हम तरंग दैर्ध्य को मापते हैं, लेकिन चरण में देरी। दूसरे शब्दों में

गुरुत्वाकर्षण तरंग डिटेक्टर एक शासक की तरह नहीं, एक घड़ी की तरह काम करता है।

5. निष्कर्ष

यह जोर देना महत्वपूर्ण है कि गुरुत्वाकर्षण तरंग दर्पण के बीच की दूरी की तुलना में प्रकाश की तरंग दैर्ध्य को अलग तरह से प्रभावित करती है। यह मुख्य रूप से इस तथ्य के कारण है कि जीडब्ल्यू की अवधि प्रकाश के आगे और पीछे जाने के समय की तुलना में बहुत अधिक है। GW की अवधि के बाद इंटरफेरोमीटर का हाथ समय के साथ बढ़ता रहता है, और प्रकाश लगातार लेजर से "नया" आ रहा है।

इसके अलावा, असली डिटेक्टर में अतिरिक्त दर्पण होते हैं जो कई गुंजयमान यंत्र बनाते हैं, जो कंधे की लंबाई को प्रभावी ढंग से बढ़ाते हैं। हालांकि, यह मुख्य विचार को प्रभावित नहीं करता है।

इसलिए हम वास्तव में गुरुत्वाकर्षण तरंगों का निरीक्षण कर सकते हैं, और कोई साजिश सिद्धांत नहीं!

छवि क्रेडिट: www.ligo.caltech.edu

6. LIGO समाचार

एक पोस्टस्क्रिप्ट के रूप में, अब LIGO में क्या हो रहा है, इसके बारे में थोड़ा। O2 के अवलोकनों के दूसरे चक्र में न केवल न्यूट्रॉन सितारों के संलयन का अवलोकन और एचएस का पहला संयुक्त अवलोकन तीन डिटेक्टरों द्वारा किया गया , जिसमें कन्या भी शामिल है, लेकिन कई अन्य घटनाएं भी हैं। बहुत निकट भविष्य में, डेटा विश्लेषण के परिणाम प्रकाशित किए जाएंगे, और डेटा स्वयं खुला और विश्लेषण के लिए उपलब्ध होगा।

LIGO अब कई अपडेट पूरा कर रहा है, जिसमें संपीड़ित प्रकाश की स्थापना और एक अधिक शक्तिशाली लेजर शामिल है, जो डिटेक्टर की संवेदनशीलता को कई गुना बढ़ा देगा और आपको बहुत अधिक घटनाओं (एक अच्छे परिदृश्य में - प्रति सप्ताह घटना द्वारा) का निरीक्षण करने की अनुमति देगा।

अगले साल की शुरुआत में, एक नया ओ 3 अवलोकन चक्र शुरू होगा।