एबीसी परिकल्पना का संख्यात्मक सत्यापन (हाँ, यह एक)

हाय, हैब्र।

Geektimes Habr (उदाहरण के लिए, 2013 और 2018 में ) पर abc परिकल्पना पर पहले ही कई लेख आ चुके हैं। एक प्रमेय के बारे में कहानी जो पहले कई वर्षों के लिए साबित नहीं की जा सकती है, और फिर एक ही संख्या में वर्षों के लिए सत्यापित नहीं की जा सकती है, निश्चित रूप से कम से कम एक फीचर फिल्म की हकदार है। लेकिन इस अद्भुत कहानी की छाया में, प्रमेय को बहुत ही सतही रूप से माना जाता है, हालांकि यह कम दिलचस्प नहीं है। पहले से ही कम से कम तथ्य यह है कि एबीसी परिकल्पना आधुनिक विज्ञान की कुछ अनसुलझी समस्याओं में से एक है, इस समस्या का बयान जो एक पांचवें ग्रेडर को भी समझ सकता है। यदि यह परिकल्पना वास्तव में सच है, तो यह आसानी से अन्य महत्वपूर्ण प्रमेयों के प्रमाण से अनुसरण करता है, उदाहरण के लिए, फर्मेट के प्रमेय का प्रमाण।

मोतीज़ुकी लॉरेल्स का दावा किए बिना, मैंने भी कोशिश करने का फैसला किया और एक कंप्यूटर के साथ जांच करने का फैसला किया कि परिकल्पना में कितना समानता का वादा किया गया है। वास्तव में, क्यों नहीं - आधुनिक प्रोसेसर न केवल गेम खेलने के लिए हैं - क्यों इसके मुख्य (गणना) उद्देश्य के लिए एक कंप्यूटर का उपयोग न करें ...

बिल्ली के नीचे, कृपया क्या हुआ, कौन परवाह करता है।

समस्या का बयान

शुरू से शुरू करते हैं। प्रमेय के बारे में क्या है? जैसा कि विकिपीडिया कहता है (अंग्रेजी संस्करण में शब्दांकन थोड़ा अधिक स्पष्ट है), पारस्परिक रूप से अभाज्य (सामान्य भाजक नहीं होने पर) संख्या a, b और c ऐसी है कि a + b = c, किसी भी 0> 0 के लिए सीमित संख्या में triples है a + b = c, ऐसे:



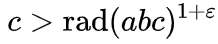
रेड फ़ंक्शन को रेडिकल कहा जाता है, और किसी संख्या के प्रमुख कारकों के उत्पाद को दर्शाता है। उदाहरण के लिए, रेड (16) = रेड (2 * 2 * 2 * 2) = 2, रेड (17) = 17 (17 एक प्राइम), रेड (18) = रेड (2 * 3 * 3) = 2 * 3 = 6, रेड (1,000,000) = रेड (2 ^ 6 6 5 ^ 6) = 2 * 5 = 10।

दरअसल, प्रमेय का सार यह है कि ऐसे त्रिगुणों की संख्या काफी कम है। उदाहरण के लिए, यदि हम यादृच्छिक ε = 0.2 और समानता 100 + 27 = 127: रेड (100) = रेड (2 * 2 * 5 * 5) = 10, रेड (27) = रेड (3 * 3 * 3) = 3 लेते हैं, rad (127) = 127, rad (a * b * c) = rad (a) * rad (b) * rad (c) = 3810, 3810 ^ 1.2 स्पष्ट रूप से 127 से अधिक है, असमानता धारण नहीं करती है। लेकिन अपवाद हैं, उदाहरण के लिए, समानता 49 + 576 = 625 के लिए, प्रमेय की शर्त पूरी होती है (जो लोग अपने दम पर जांच कर सकते हैं)।

हमारे लिए अगला महत्वपूर्ण क्षण प्रमेय के अनुसार सीमित संख्या में है। यानी इसका मतलब है कि आप बस उन सभी को कंप्यूटर पर छांटने की कोशिश कर सकते हैं। नतीजतन, यह हमें नोबेल पुरस्कार काफी रोचक प्रोग्रामिंग कार्य देता है।

तो चलिए शुरू करते हैं।

स्रोत कोड

पहला संस्करण पायथन में लिखा गया था, और हालांकि यह भाषा ऐसी गणनाओं के लिए बहुत धीमी है, इस पर कोड लिखना आसान और सरल है, जो प्रोटोटाइप के लिए सुविधाजनक है।

रेडिकल प्राप्त करना : हम संख्या को प्रमुख कारकों में विघटित करते हैं, फिर पुनरावृत्तियों को हटाते हैं, सरणी को एक सेट में परिवर्तित करते हैं। फिर बस सभी तत्वों का उत्पाद प्राप्त करें।

def prime_factors(n): factors = [] # Print the number of two's that divide n while n % 2 == 0: factors.append(int(2)) n = n / 2 # n must be odd at this point so a skip of 2 ( i = i + 2) can be used for i in range(3, int(math.sqrt(n)) + 1, 2): # while i divides n , print i ad divide n while n % i == 0: factors.append(int(i)) n = n / i # Condition if n is a prime number greater than 2 if n > 2: factors.append(int(n)) return set(factors) def rad(n): result = 1 for num in prime_factors(n): result *= num return result 

पारस्परिक रूप से अभाज्य संख्याएँ : संख्याओं का गुणनखंड, और केवल समुच्चयों के प्रतिच्छेदन की जाँच करें।

 def not_mutual_primes(a,b,c): fa, fb, fc = prime_factors(a), prime_factors(b), prime_factors(c) return len(fa.intersection(fb)) == 0 and len(fa.intersection(fc)) == 0 and len(fb.intersection(fc)) == 0 

जांचें : हम पहले से ही बनाए गए कार्यों का उपयोग करते हैं, यहां सब कुछ सरल है।

 def check(a,b,c): S = 1.2 # Eps=0.2 if c > (rad(a)*rad(b)*rad(c))**S and not_mutual_primes(a, b, c): print("{} + {} = {} - PASSED".format(a, b, c)) else: print("{} + {} = {} - FAILED".format(a, b, c)) check(10, 17, 27) check(49, 576, 625) 

जो लोग उपरोक्त कोड को किसी भी ऑनलाइन पायथन भाषा संपादक में कॉपी करके स्वतंत्र रूप से प्रयोग कर सकते हैं। बेशक, कोड उम्मीद के मुताबिक चलता है, और कम से कम एक मिलियन के लिए सभी परीक्षणों की गणना करना बहुत लंबा होगा। स्पॉइलर के नीचे एक अनुकूलित संस्करण है, इसका उपयोग करने की अनुशंसा की जाती है।

अंतिम संस्करण को C ++ में मल्टीथ्रेडिंग और कुछ ऑप्टिमाइज़ेशन का उपयोग करके फिर से लिखा गया था (इंटरसेक्टिंग सेट के साथ सी में काम करना बहुत कट्टर होगा, हालांकि शायद तेज है)। स्रोत कोड स्पॉइलर के नीचे है, इसे मुफ्त जी ++ संकलक में संकलित किया जा सकता है, कोड विंडोज, ओएसएक्स और यहां तक ​​कि रास्पबेरी पाई के तहत काम करता है।


उन लोगों के लिए जो C ++ कंपाइलर को स्थापित करने के लिए बहुत आलसी हैं, एक थोड़ा अनुकूलित पायथन संस्करण प्रदान किया गया है, जिसे किसी भी ऑनलाइन संपादक में चलाया जा सकता है (मैंने https://repl.it/languages/python का उपयोग किया है)।

परिणाम

त्रिक a, b, c वास्तव में बहुत कम हैं।

कुछ परिणाम नीचे दिए गए हैं:
एन = 10 : 1 "तीन", लीड समय <0.001c
1 + 8 = 9

एन = 100 : 2 "ट्रिपल्स", रनटाइम <0.001 सी
1 + 8 = 9
1 + 80 = 81

एन = 1000 : 8 "ट्रिपल्स", रनटाइम <0.01c
1 + 8 = 9
1 + 80 = 81
1 + 242 = 243
1 + 288 = 289
1 + 512 = 513
3 + 125 = 128
13 + 243 = 256
49 + 576 = 625

एन = 10000 : 23 "ट्रिपल्स", रनटाइम 2 एस


एन = 100000 : 53 ट्रिपल्स, रनटाइम 50 सी


एन = 1,000,000 के साथ, हमारे पास केवल 102 "ट्रिपल्स" हैं, स्पॉइलर के तहत एक पूरी सूची दी गई है।


काश, कार्यक्रम अभी भी धीरे-धीरे काम करता है, मैंने एन = 10,000,000 के लिए परिणामों की प्रतीक्षा नहीं की, गणना का समय एक घंटे से अधिक है (शायद मैंने कहीं एल्गोरिदम को अनुकूलित करने के साथ गलती की, और मैं बेहतर कर सकता हूं)।

और भी दिलचस्प परिणाम को रेखांकन के साथ देखना है:



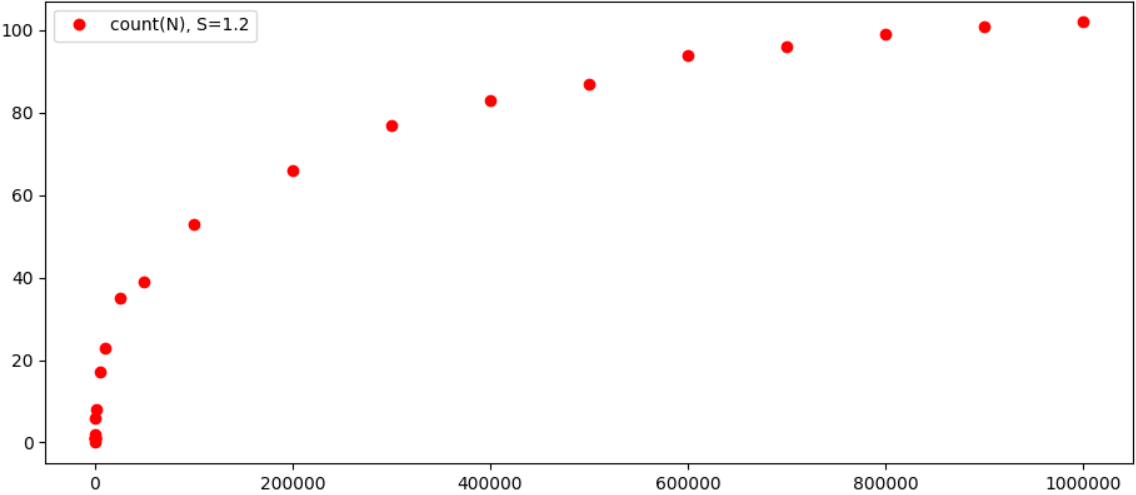
सिद्धांत रूप में, यह काफी स्पष्ट है कि एन पर संभावित त्रिगुणों की संख्या की निर्भरता एन की तुलना में काफी धीमी हो जाती है, और यह संभावना है कि परिणाम प्रत्येक each के लिए कुछ विशिष्ट संख्या में परिवर्तित हो जाएगा। वैसे, ε में वृद्धि के साथ, "triples" की संख्या में उल्लेखनीय रूप से कमी आती है, उदाहरण के लिए,, = 0.4 के लिए हमारे पास N <100000 (1 + 4374 = 4375 और 34,0 + 59049 = 59392) के लिए केवल 2 समानताएँ हैं। तो सामान्य तौर पर, ऐसा लगता है कि प्रमेय वास्तव में (अच्छी तरह से, और शायद यह पहले से ही अधिक शक्तिशाली कंप्यूटरों पर परीक्षण किया गया है, और शायद यह सब लंबे समय से गणना की गई है)।

जो लोग अपने दम पर प्रयोग कर सकते हैं, अगर किसी के पास 10,000,000 और अधिक संख्या के लिए परिणाम हैं, तो मुझे उन्हें लेख में जोड़ने में खुशी होगी। बेशक, यह "गिनती" करने के लिए दिलचस्प होगा जब तक कि "ट्रिपल" का सेट पूरी तरह से बढ़ना बंद हो जाता है, लेकिन यह वास्तव में लंबा समय ले सकता है, गणना की गति एन के रूप में एन * एन (या शायद एन ^ 3) पर निर्भर करती है, और प्रक्रिया बहुत लंबा। फिर भी, एक आश्चर्यजनक चीज पास में है, और जो लोग चाहते हैं वे खोज में शामिल हो सकते हैं।

संपादित करें: जैसा कि टिप्पणियों में सुझाया गया है, विकिपीडिया में पहले से ही परिणामों के साथ एक तालिका है - एन में 10 ^ 18 तक की सीमा में "ट्रिपल" की संख्या अभी भी बढ़ रही है, इसलिए सेट का "अंत" अभी तक नहीं मिला है। सभी अधिक दिलचस्प - साज़िश अभी भी संरक्षित है।