👨🏽‍🍳 🤰🏿 🧜🏾 TensorFlow पर तंत्रिका नेटवर्क के अनुकूलन के लिए लेवेनबर्ग-मार्क्वर्ट एल्गोरिथ्म का कार्यान्वयन ✊🏼 👸🏿 🙋🏻

यह एक TensorFlow लाइब्रेरी ट्यूटोरियल है। हस्तलिखित संख्याओं की मान्यता पर लेखों की तुलना में इसे थोड़ा गहरा मानें। यह अनुकूलन विधियों पर एक ट्यूटोरियल है। यहां आप गणित के बिना नहीं कर सकते। यह ठीक है अगर आप इसे पूरी तरह से भूल गए। याद। कोई औपचारिक सबूत और जटिल निष्कर्ष नहीं होगा, केवल सहज समझ के लिए आवश्यक न्यूनतम। शुरुआत करने के लिए, इस एल्गोरिथ्म पर एक छोटी पृष्ठभूमि कैसे तंत्रिका नेटवर्क के अनुकूलन में उपयोगी हो सकती है।

छह महीने पहले, एक मित्र ने मुझे यह दिखाने के लिए कहा कि पायथन में एक तंत्रिका नेटवर्क कैसे बनाया जाए। उनकी कंपनी भूभौतिकीय मापन के लिए उपकरणों का उत्पादन करती है। ड्रिलिंग के दौरान कई अलग-अलग जांच कुओं के आसपास के वातावरण के मापदंडों से जुड़े संकेतों के एक सेट को मापते हैं। कुछ जटिल मामलों में, एक शक्तिशाली कंप्यूटर पर भी लंबे समय तक संकेतों से पर्यावरणीय मापदंडों की सटीक गणना करें, और क्षेत्र में माप परिणामों की व्याख्या करना आवश्यक है। एक क्लस्टर पर कई सौ हजार मामलों की गणना करने और उन पर एक तंत्रिका नेटवर्क को प्रशिक्षित करने का विचार था। चूंकि तंत्रिका नेटवर्क बहुत तेज है, इसका उपयोग उन मापदंडों को निर्धारित करने के लिए किया जा सकता है जो मापा संकेतों के अनुरूप हैं, ड्रिलिंग की प्रक्रिया में सही हैं। विवरण लेख में हैं:

कुशनिर, डी।, वेलकर, एन।, बोंडारेंको, ए।, डायटलोव, जी।, और दासहेवस्की, वाई। (2018, 29 अक्टूबर)। तंत्रिका नेटवर्क (रूसी) का उपयोग करके 2 डी फॉल्ट मॉडल में डीप अजीमुथल प्रतिरोधकता उपकरण का वास्तविक समय सिमुलेशन। पेट्रोलियम इंजीनियर्स का समाज। doi: 10.2118 / 192573-RU

एक शाम, मैंने दिखाया कि कैसे केर एक सरल तंत्रिका नेटवर्क को लागू कर सकते हैं, और काम पर एक मित्र ने गिने हुए डेटा पर प्रशिक्षण शुरू किया। कुछ दिनों के बाद, हमने परिणाम पर चर्चा की। मेरे दृष्टिकोण से, वह आशाजनक लग रहा था, लेकिन एक दोस्त ने कहा कि उसे डिवाइस की सटीकता के साथ गणना की आवश्यकता थी। और अगर औसत चुकता त्रुटि 1 के आसपास हो गई, तो 1e-3 की आवश्यकता थी। 3 आदेश कम। एक हजार बार।

तंत्रिका नेटवर्क वास्तुकला, डेटा सामान्यीकरण, और अनुकूलन दृष्टिकोण के साथ प्रयोग लगभग कुछ भी नहीं मिला। कुछ हफ़्ते बाद, एक दोस्त ने फोन किया और कहा कि उसने माटलैब स्थापित किया और लेवेनबर्ग-मार्क्वार्ड विधि द्वारा समस्या को हल किया (इसके बाद हम एलएम को कॉल करेंगे)। यह लंबे समय (कई दिनों) के लिए अनुकूलित किया गया था, यह GPU पर काम नहीं करता था, लेकिन परिणाम सही था। यह एक चुनौती की तरह लग रहा था।

कैरस या टेंसॉरफ्लो के लिए तैयार एलएम ऑप्टिमाइज़र की एक त्वरित खोज विफल रही। मैं केवल पाइरन लाइब्रेरी में आया था, लेकिन इसकी कार्यक्षमता मुझे खराब लग रही थी। मैंने खुद इसे लागू करने का फैसला किया। पहली नज़र में, सब कुछ सरल लग रहा था, और दो शामें पर्याप्त होनी चाहिए थीं। इसमें अधिक समय लगा। दो समस्याएं थीं:

TensorFlow। लेखों का एक समूह, लेकिन लगभग सभी स्तरों "लेकिन चलो ~~हैलो विश्व~~ हस्तलिखित अंक मान्यता लिखते हैं।"
गणित। मैं बहुत कुछ भूल गया, और गणितीय लेखों के लेखकों को मेरे जैसे लोगों के बारे में बिल्कुल परवाह नहीं है: स्पष्टीकरण के बिना ठोस सूत्र, "जाहिर है!" और इसी तरह।

नतीजतन, उन्होंने उन लोगों के लिए एक लेख लिखा जो गणित भूल गए और टेंसोरफ्लो को थोड़ा गहराई से समझना चाहते हैं, लेकिन कट्टर के बिना। लेख में बहुत सारे पाठ और छोटे कोड हैं। विपरीत विकल्प, जब थोड़ा पाठ और बहुत सारे कोड होते हैं, तो यहां ज्यूपिटर नोटबुक लीवेनबर्ग-मार्क्वार्ड है ।

रोसेनब्रॉक सुविधा को जानिए

हम रोसेनब्रॉक फ़ंक्शन द्वारा प्रशिक्षण डेटा उत्पन्न करेंगे, जिसे अक्सर अनुकूलन एल्गोरिदम के लिए बेंचमार्क के रूप में उपयोग किया जाता है:

$f (x, y) = (a-x) ^ 2 + b (y-x ^ 2) ^ 2$

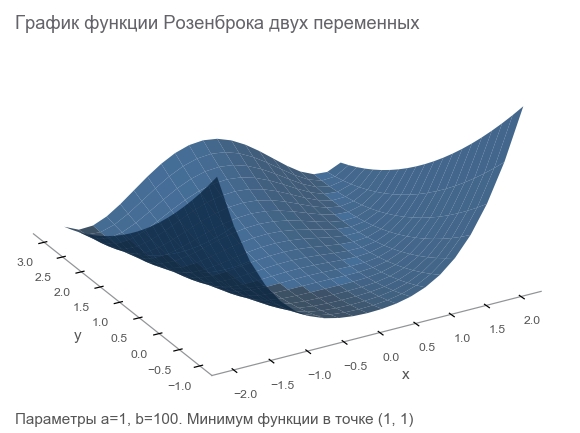
वह अच्छी क्यों है?

सुंदर अनुसूची। इसे रोसेनब्रॉक वैली और अनट्रांसबल रोसेनब्रोक की केला फंक्शन कहा जाता है।
वैश्विक न्यूनतम लंबी, संकीर्ण, परवलयिक समतल घाटी के अंदर है। एक घाटी ढूँढना तुच्छ है, और एक वैश्विक न्यूनतम मुश्किल है।
एक बहुआयामी विकल्प है। कई चरों के लिए अच्छे कार्य के साथ आना इतना आसान नहीं है।

हम आगे के काम के लिए आवश्यक पुस्तकालयों को जोड़कर इससे कोड लिखना शुरू करेंगे:

import numpy as np import tensorflow as tf import math def rosenbrock(x, y, a, b): return (a - x)**2 + b*(y - x**2)**2

हम समस्या बताते हैं

जब से हम एक मापने वाले उपकरण के बारे में बात कर रहे थे, तो हम सादृश्य का उपयोग करना जारी रखते हैं। एक काल्पनिक दुनिया में हमारा उपकरण निर्देशांक को माप सकता है $(x, y)$ और ऊंचाई $z$ । भौतिकविदों ने दुनिया का अध्ययन किया और कहा: " हां, यह रोसेनब्रोक है! निर्देशांक को जानने के बाद, आप ऊंचाई की सही गणना कर सकते हैं, आपको इसे मापने की आवश्यकता नहीं है। " दूसरे शब्दों में, वैज्ञानिकों ने हमें एक मॉडल दिया $z = रोसब्रुक (एक्स, वाई, ए, बी)$ जो मापदंडों पर निर्भर करता है $(ए, बी)$ । ये पैरामीटर, हालांकि एक काल्पनिक दुनिया में स्थिर हैं, अज्ञात हैं। उन्हें ढूंढने की जरूरत है।

हमने प्रयोगों की एक श्रृंखला आयोजित की, जो दिए गए $एम$ अंक $(x_1, y_1, z_1), (x_2, y_2, z_2), ..., (x_m, y_m, z_m)$ :

 # (2.5, 2.5) -   ,  ,     data_points = np.array([[x, y, rosenbrock(x, y, 2.5, 2.5)] for x in np.arange(-2, 2.1, 2) for y in np.arange(-2, 2.1, 2)]) m = data_points.shape[0]

ऑप्टिमाइज़ करने का पहला तरीका मापदंडों की कोशिश और अनुमान लगाना है। हम Numpy लाइब्रेरी का उपयोग करते हैं:

 x, y = data_points[:, 0], data_points[:, 1] z = data_points[:, 2] #   =5  b=5? a_guess, b_guess = 5., 5. #  -hat   ,   , #   ,   ,   .   #     ^   - # .    hat. z_hat = rosenbrock(x, y, a_guess, b_guess)

कैसे समझें कि हम कितने गलत हैं? अवशिष्टों की गणना करें - त्रुटि आकार। $एम$ अंक देते हैं $एम$ अवशिष्ट - आपको एक अभिन्न संकेतक की आवश्यकता होती है। हम प्रत्येक अवशिष्ट को एक वर्ग में रखते हैं और औसत की गणना करते हैं:

$MSE (a, b) = \ frac {1} {m} \ sum_ {i = 1} ^ {m} (z_ {i} - \ widehat {z_ {i}}) 2$

निकटता के इस माप को माध्य चुकता त्रुटि कहा जाता है (बाद में इसे mse कहा जाता है):

 # r - residuals () r = z - z_hat # mse loss = np.mean(r**2) print(loss)

 [Out]: 3868.2291666666665

न्यूनतम को कम करके , हम कम से कम वर्गों की समस्या को हल करते हैं ( गैर-वर्ग वर्ग न्यूनतम ):

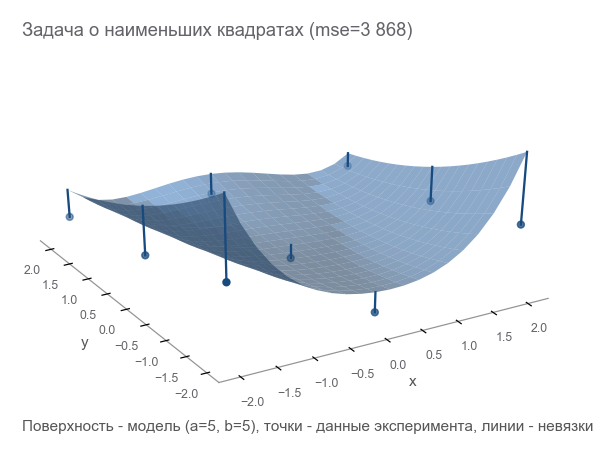
यह देखा जा सकता है कि मापदंडों का अनुमान बिल्कुल नहीं था।

हम TensorFlow पर समस्या तैयार करते हैं

मॉडल का रूप है $z = रोसब्रुक (एक्स, वाई, ए, बी)$ । हम इसे फॉर्म में लाते हैं $y = f (x, p)$ (आमतौर पर मैथ्स लिखते हैं $\ बीटा$ के बजाय $पी$ लेकिन प्रोग्रामर बीटा का उपयोग नहीं करते हैं)। अब मॉडल का रूप है $y = रोसेनब्रोक (एक्स, पी)$ जहाँ $य$ - ऊंचाई $x$ दो तत्वों (घटक), और का समन्वय वेक्टर है $पी$ - मापदंडों का वेक्टर ।

प्रोग्रामर अक्सर वैक्टर को एक आयामी सरणियों के रूप में सोचते हैं। यह पूरी तरह सही नहीं है। संख्याओं की एक सरणी एक वेक्टर का प्रतिनिधित्व करने का एक साधन है। आप एक वेक्टर को आयाम के एक सरणी के रूप में दर्शा सकते हैं $एन$ , दो आयामी सरणी $1 \ N बार$ , और यहां तक कि एक सरणी $एन \ _ 1$ उन मामलों में जहां तथ्य यह है कि वेक्टर एक कॉलम वेक्टर है (उदाहरण के लिए, इसके द्वारा मैट्रिक्स को गुणा करना) महत्वपूर्ण है:

$\ start {bmatrix} x_1 \\\ vdots \\ x_N \ end {bmatrix}$

TensorFlow टेंसर की अवधारणा का उपयोग करता है। एक टेंसर , एक सरणी की तरह, एक आयामी (एक वेक्टर का प्रतिनिधित्व करने के लिए), दो-आयामी (एक मैट्रिक्स या स्तंभ वेक्टर के लिए ) और किसी भी बड़े आयाम हो सकता है।

 #    ('placeholder' ,    #      ) x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m]) #   ('variable' ,    ) #     (5, 5) p = tf.Variable([5., 5.], dtype=tf.float64) #  y_hat = rosenbrock(x[:, 0], x[:, 1], p[0], p[1]) #  r = y - y_hat # mse (mean squared error) loss = tf.reduce_mean(r**2)

TensorFlow कोड Numpy कोड से अलग नहीं है। सामग्री बहुत बड़ी है। Numpy कोड mse मान की गणना करता है । TensorFlow कोड किसी भी गणना को पूरा नहीं करता है, यह एक डेटा फ्लो ग्राफ बनाता है जो mse गणना कर सकता है । एक बहुत दिमाग- सहनशील क्षण रोसब्रुक फ़ंक्शन का काम है। हम इसे दोनों मामलों में उपयोग करते हैं। लेकिन जब हम Numpy सरणियों को पास करते हैं, तो यह सूत्र के अनुसार गणना करता है और संख्याओं को वापस करता है। और जब हम टेंसरों को TensorFlow में स्थानांतरित करते हैं, तो यह डेटा स्ट्रीम का एक सबग्राफ बनाता है और एक टेंसर के रूप में अपनी बढ़त देता है। बहुरूपता के चमत्कार, लेकिन उनका दुरुपयोग न करें:

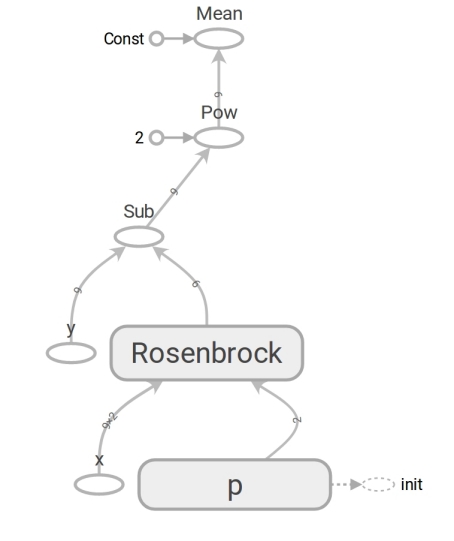
इस तरह के एक डेटा प्रवाह ग्राफ की उपस्थिति के लिए धन्यवाद, TensorFlow विशेष रूप से स्वचालित रूप से डेरिवेटिव की गणना करने में सक्षम है ( रिवर्स मोड स्वत: भिन्न तकनीक का उपयोग करके)।

गणित का एक क्षण। ब्लॉक "उन लोगों के लिए जो भूल गए हैं" एक स्पॉइलर में छिपाया जाएगा।

व्युत्पन्न (संख्या दर्ज - संख्या शेष)

सबसे अधिक संभावना है कि आपको एक स्केलर के व्युत्पन्न की परिभाषा याद है (एक संख्या लौटना) एक चर का कार्य: के लिए $f: \ mathbb {R} \ rightarrow \ mathbb {R}$ यौगिक $च$ बिंदु पर $x \ in \ mathbb {R}$ के रूप में परिभाषित:

${f} '(x) = \ lim_ {h \ to 0} \ frac {f (x + h) -f (x)} {h}$

डेरिवेटिव्स परिवर्तन को मापने का एक तरीका है। स्केलर मामले में, व्युत्पन्न दिखाता है कि फ़ंक्शन कितना बदल जाएगा $च$ अगर $x$ एक छोटे से मूल्य में परिवर्तन $\ _ varepsilon$ :

$f (x + \ varepsilon) \ लगभग f (x) + \ varepsilon {f} '(x)$

सुविधा के लिए, हम निरूपित करते हैं $य = च (x)$ , और व्युत्पन्न $य$ पर $x$ हम लिखेंगे कि कैसे $\ frac {\ आंशिक y} {\ आंशिक x}$ । ऐसा रिकॉर्ड इस बात पर जोर देता है $\ frac {\ आंशिक y} {\ आंशिक x}$ - चर के बीच परिवर्तन की दर $x$ और $य$ । अधिक विशेष रूप से, यदि $x$ को बदलो $\ _ varepsilon$ तो $य$ लगभग बदल जाना $\ varepsilon \ frac {\ आंशिक y} {\ आंशिक x}$ । आप इसे इस तरह भी लिख सकते हैं:

$x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ लगभग y + \ frac {\ आंशिक y} {\ आंशिक x} \ Delta x$

के रूप में पढ़ता है: "बदल रहा है $x$ पर $x + \ Delta x$ परिवर्तन $य$ लगभग $y + \ Delta x \ frac {\ आंशिक y} {\ आंशिक x}$ "इस तरह के एक रिकॉर्ड स्पष्ट रूप से परिवर्तन के बीच की कड़ी को उजागर करता है $x$ और बदल जाते हैं $य$ ।

हमने एक डेटा फ्लो ग्राफ बनाया है, चलो गणना गणना चलाते हैं:

 #        #      placeholder (  ) feed_dict = {x: data_points[:,0:2], y: data_points[:,2]} #       TensorFlow session = tf.Session() #     session.run(tf.global_variables_initializer()) #   ()  loss (mse) current_loss = session.run(loss, feed_dict) print(current_loss)

 [Out]: 3868.2291666666665

नतीजा नेम्पी के साथ भी ऐसा ही है। इसलिए उनसे गलती नहीं हुई।

अनुकूलन शुरू करें

दुर्भाग्य से, मापदंडों का अनुमान लगाना संभव नहीं था। लेकिन फिर हम:

हम इष्टतम मानदंड निर्धारित करते हैं - न्यूनतम मूल्य।
चर पैरामीटर निर्धारित किए गए थे: वेक्टर $पी$ घटकों के साथ $एक$ । $ब$ रोसेनब्रक कार्य करता है।
हमने अभी तक सीमाओं के बारे में नहीं सोचा है, लेकिन वे वहां नहीं हैं।

अंतिम चरण में, हमने एक परिमित हानि टेंसर ( हानि फ़ंक्शन ) के साथ डेटा प्रवाह ग्राफ का निर्माण किया। अनुकूलन का लक्ष्य पैरामीटर वेक्टर के मूल्य को खोजना है $पी$ जिस पर नुकसान फ़ंक्शन का मूल्य न्यूनतम है। हम भाग्यशाली थे, इस समारोह का ग्राफ बहुत सरल है (अवतल और स्थानीय मीनिमा के बिना):

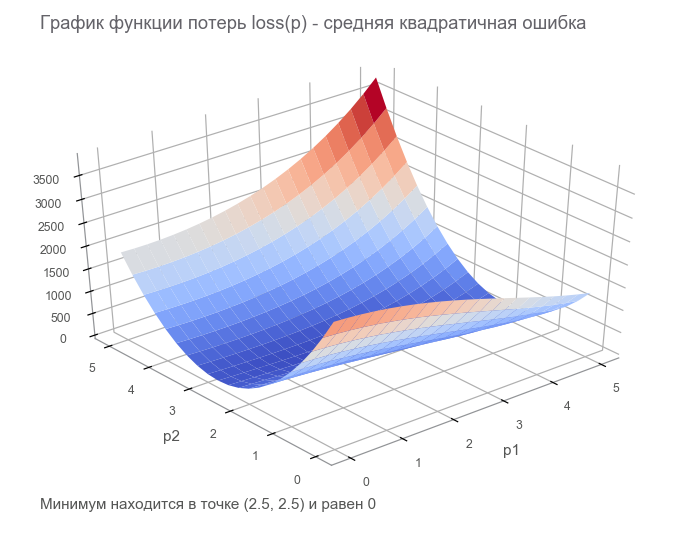
अनुकूलन के साथ शुरुआत करना। शुरू करने के लिए, हम एक सामान्यीकृत चक्र लिखते हैं:

 # :   mse,   ,  #   mse,        placeholder def train(target_loss, max_steps, loss_tensor, train_step_op, inputs): step = 0 current_loss = session.run(loss_tensor, inputs) #           while current_loss > target_loss and step < max_steps: step += 1 #    1, 2, 4, 8, 16...  if math.log(step, 2).is_integer(): print(f'step: {step}, current loss: {current_loss}') #    session.run(train_step_op, inputs) current_loss = session.run(loss_tensor, inputs) print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}')

हम सबसे तेज़ ढाल डिसेंट (SGD) की विधि से अनुकूलन करते हैं

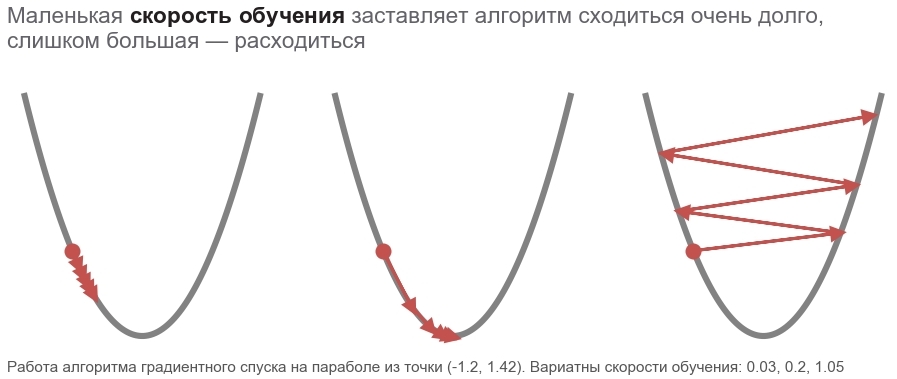
इस पद्धति के कार्यों की तुलना एक साहसी स्कीयर की सवारी से की जा सकती है, जो हमेशा ढलान (सबसे स्थिर दिशा में) को नीचे रखता है। इस मामले में, स्थान के बिंदु पर केवल ढलान को ध्यान में रखा जाता है। और अगर ढलान मजबूत है, तो स्कीयर अगले बदलाव से पहले एक लंबी दूरी की उड़ान भरता है। कमजोर ढलान के साथ, यह छोटे चरणों में चलता है। शायद उड़ने का तरीका ~~एक पेड़ में~~ ( एल्गोरिथ्म विचलन ), और एक गड्ढे ( स्थानीय न्यूनतम ) में फंस जाते हैं।

आप इस प्रकार (परिवर्तन) लिख सकते हैं $\ boldsymbol {p}$ पर $\ _ सुनार {p} - ...$ ):

$\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _। सुनहरा $ {सुनार {{}} दायाँ भौंरा \ _ \$

फैटी $\ boldsymbol {p}$ जोर देता है कि यह वास्तविक स्थान का बिंदु है - वर्तमान कदम पर पैरामीटर वेक्टर का मूल्य। पहले कदम पर, यह हमारा अनुमान है (5, 5)। सूत्र में दो दिलचस्प बिंदु हैं: $\ अल्फा$ - सीखने की दर ( सीखने की दर ), $\ nabla_ {p} हानि$ - मापदंडों के वेक्टर द्वारा नुकसान समारोह के ढाल ( ढाल )।

ग्रेडिएंट (वेक्टर दर्ज किया गया - नंबर बाईं ओर)

एक फ़ंक्शन पर विचार करें जो एक वेक्टर को इनपुट के रूप में लेता है और एक स्केलर का उत्पादन करता है: $f: \ mathbb {R} ^ {N} \ rightarrow \ mathbb {R}$ । यौगिक $च$ बिंदु पर $x \ in \ mathbb {R} ^ {N}$ अब एक ढाल कहा जाता है और एक वेक्टर है $[\ nabla_ {x} f (x)] in \ mathbb {R} ^ {N}$ ("नाबला" के रूप में पढ़ा) आंशिक व्युत्पन्न से बना:

$\ nabla_ {x} y = (\ frac {\ आंशिक y} {\ आंशिक x_ {1}}, \ frac {\ आंशिक y} {\ आंशिक x_ {2}}, ..., \ frac {\ आंशिक y} {\ आंशिक x_ {N}})$

इस मामले के लिए, तर्क के परिवर्तन पर फ़ंक्शन के परिवर्तन की निर्भरता का रिकॉर्ड निम्नानुसार है:

$x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ लगभग y + \ nabla_ {x} y \ cdot \ Delta x$

उस खाते को लेने के लिए रिकॉर्ड काफी बदल गया है $x$ । $\ Delta x$ और $\ nabla_ {x} y$ - वैक्टर में $\ mathbb {R} ^ {N}$ , और $य$ - स्केलर। जब कई गुणा वैक्टर $\ nabla_ {x} y$ और $\ Delta x$ स्केलर उत्पाद का उपयोग किया जाता है (घटकों के उत्पादों का योग)।

 #        grad = tf.gradients(loss, p)[0] #   learning_rate = 0.0005 #   ,     apply_gradients - #         opt = tf.train.GradientDescentOptimizer(learning_rate=1) #           sgd = opt.apply_gradients([(learning_rate*grad, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, sgd, feed_dict) print('PARAMETERS:', session.run(p))

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 1381.5379689135807 [...] ENDED ON STEP: 582, FINAL LOSS: 9.698531012270816e-11 PARAMETERS: [2.50000205 2.49999959]

इसने 582 कदम उठाए:

एंटी-ग्रेडिएंट की दिशा में आंदोलन

हम ढाल के विपरीत क्यों बढ़ रहे हैं? स्केलर उत्पाद के साथ प्रविष्टि को याद करें: $x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ लगभग y + \ nabla_ {x} y \ cdot \ Delta x$ । कम से कम $य$ । चूंकि फ़ंक्शन के व्यवहार को व्युत्पन्न के माध्यम से केवल एक छोटे से पड़ोस में जाना जाता है, इसलिए यह छोटे, लेकिन इष्टतम चरणों में, उत्पाद को छोटा करने के लिए आवश्यक है। $\ nabla_ {x} y \ cdot \ Delta x$ । स्कूल की परिभाषा के अनुसार, दो वैक्टरों का स्केलर उत्पाद उनके बीच के कोण के कोसाइन द्वारा इन वैक्टरों की लंबाई के उत्पाद के बराबर संख्या है : $a \ cdot b = \ left | a \ right | \ left | b \ right | cos \ angle (a, b)$ । वैक्टर की एक निश्चित लंबाई के लिए, यह उत्पाद न्यूनतम -1 के कोसाइन के साथ पहुंचता है, अर्थात। 180 डिग्री के कोण पर, जब वैक्टर विपरीत दिशाओं में निर्देशित होते हैं। तदनुसार, न्यूनतम स्केलर उत्पाद $\ nabla_ {x} y \ cdot \ Delta x$ जब हासिल किया $\ Delta x$ एंटी-ग्रेडिएंट की दिशा में।

हम एडम विधि द्वारा अनुकूलन करते हैं

हम आगे धीरे-धीरे तरीकों में नहीं जाएंगे, लेकिन कई विविधताएं हैं। आप उनके बारे में लेख में पढ़ सकते हैं तंत्रिका नेटवर्क के अनुकूलन के तरीके । TensorFlow में, कई ऑप्टिमाइज़र पहले से ही लागू हैं। उदाहरण के लिए, एडम:

 #       , #      adm = tf.train.AdamOptimizer(15).minimize(loss) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, adm, feed_dict) print('PARAMETERS:', session.run(p))

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 34205.72916492336 [...] ENDED ON STEP: 317, FINAL LOSS: 2.424142714263483e-12 PARAMETERS: [2.49999969 2.50000008]

317 चरणों में प्रबंधित। बहुत तेज।

हम न्यूटन की विधि द्वारा अनुकूलन करते हैं

दूसरे क्रम के तरीकों की कार्रवाई एक तर्कसंगत फ्रीराइड स्नोबोर्डर की सवारी करने के लिए की जा सकती है जो अपने मार्ग के अगले बिंदु को लंबे समय तक रोकते हैं और स्थान पर न केवल ढलान को ध्यान में रखते हैं, बल्कि वक्रता भी।

वास्तव में, ग्रेडिएंट डिसेंट तरीके और सेकंड-ऑर्डर दोनों तरीके वर्तमान बिंदु पर फ़ंक्शन को अनुमानित ( अनुमानित ) करने का प्रयास करते हैं। ग्रेडिएंट तरीके केवल बिंदु पर फ़ंक्शन के ग्राफ के ढलान पर ध्यान केंद्रित करते हैं - पहला व्युत्पन्न। पूर्वाग्रह के अलावा दूसरी-क्रम विधियां, वक्रता को ध्यान में रखती हैं , दूसरी व्युत्पन्न: "यदि वक्रता बनी रहती है, तो न्यूनतम कहां होगा?" हम गणना करते हैं और वहां जाते हैं:

इस तरह के एक सन्निकटन के निर्माण और अनुमानित न्यूनतम बिंदु की गणना करने के लिए, आप टेलर श्रृंखला का उपयोग कर सकते हैं। एक आयामी मामले के लिए, बिंदु पर एक दूसरे क्रम के बहुपद द्वारा सन्निकटन $एक$ इस तरह दिखता है:

$f (x) \ लगभग f (a) + \ _ frac {f '(a) (x-a)} {1!} + \ frac {f' '(a) (x-a) ^ 2} {2!}$

न्यूनतम पर पहुँच जाता है $x = a - \ frac {f '(a)} {f' '(a)}$ । बहुआयामी मामला अधिक गंभीर दिखता है:

हेसियन मैट्रिक्स (वेक्टर दर्ज - संख्या बाईं ओर)

हेसियन मैट्रिक्स एक वर्ग मैट्रिक्स है जो दूसरे डेरिवेटिव से बना है:

$\ boldsymbol {H} y_ {x} = \ start {bmatrix} \ frac {\ आंशिक ^ 2y} {\ आंशिक x_1 ^ 2} और \ frac {\ आंशिक ^ 2y} {\ आंशिक x_1 / आंशिक x_2} और \ \ cdots & \ frac {\ आंशिक ^ 2y} {\ आंशिक x_1 \ आंशिक x_N} \\ \ frac {\ आंशिक ^ 2y} {\ आंशिक x_2 \ आंशिक x_1} & \ frac {\ आंशिक ^ 2y} {\ आंशिक x_2 ^ 2} & \ cdots & \ frac {\ आंशिक ^ 2y} {\ आंशिक x_2 \ आंशिक x_N} \\ \ vdots & \ vdots & \ ddots & \ vdots \\ \ frac {आंशिक ^ 2y} {\ आंशिक x_N \ \ आंशिक x_1} और \ frac {\ आंशिक ^ 2y} {\ आंशिक x_N \ आंशिक x_2} & \ cdots & \ frac {\ आंशिक ^ 2y} {\ आंशिक x_N ^ 2} \ अंत {bmatrix}$

एक बिंदु पर एक ढाल और एक हेसियन मैट्रिक्स के माध्यम से एक वेक्टर के कार्य के लिए दूसरे क्रम के बहुपद का अनुमान $एक$ इस तरह दिखता है:

$f (x) \ लगभग f (a) + (xa) ^ \ intercal [\ nabla_ {x} f (a)] + \ frac {1} {2!} (xa) ^ \ intercal [boldsymbol {H] } f_ {x} (a)] (xa)$

न्यूनतम पर पहुँच जाता है $x = a - [\ boldsymbol {H} f_ {x} (a)] ^ - - 1} [\ nabla_ {x} f (a)]$ । आकार व्यावहारिक रूप से एक-आयामी मामले के साथ मेल खाता है: हमने पहले व्युत्पन्न को एक ढाल के साथ बदल दिया, दूसरे को हेसियन मैट्रिक्स के साथ और वैक्टर के साथ काम करने के लिए एक सुधार किया। आप मैट्रिक्स द्वारा वेक्टर को विभाजित नहीं कर सकते हैं, इसलिए, व्युत्क्रम मैट्रिक्स द्वारा गुणा का उपयोग किया जाता है। टी का अर्थ है, संक्रमण । सूत्र का अर्थ है कि डिफ़ॉल्ट रूप से एक वेक्टर एक स्तंभ है। ट्रांज़ोज़ एक कॉलम वेक्टर को एक पंक्ति वेक्टर में बदल देता है । TensorFlow पर लागू करते समय, इसे ध्यान में रखा जाना चाहिए, लेकिन विपरीत दिशा में: डिफ़ॉल्ट रूप से, वेक्टर एक स्ट्रिंग (एक-आयामी टेंसर) है। बस के मामले में: वाष्पोत्सर्जन 90 डिग्री का एक घुमाव नहीं है, यह एक ही क्रम में पंक्तियों में पंक्तियों का परिवर्तन है।

तो, न्यूटन विधि के कदम के निम्नलिखित रूप हैं:

$\ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ \ _ to )]$

TensorFlow में इस विधि को लागू करने के लिए सब कुछ है:

 #        hess = tf.hessians(loss, p)[0] #    - grad_col = tf.expand_dims(grad, -1) # ,      dp = tf.matmul(tf.linalg.inv(hess), grad_col) #  -  - dp = tf.squeeze(dp) #  p  dp    newton = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, newton, feed_dict) print('PARAMETERS:', session.run(p))

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 105.04357496954218 step: 4, current loss: 9.96663526704236 ENDED ON STEP: 6, FINAL LOSS: 5.882202372519996e-20 PARAMETERS: [2.5 2.5]

पर्याप्त 6 चरण:

गॉस-न्यूटन एल्गोरिथ्म द्वारा अनुकूलित

न्यूटन की विधि में एक दोष है - हेसियन मैट्रिक्स। TensorFlow की बदौलत हम इसे कोड की एक पंक्ति में गिन सकते हैं। विकी के अनुसार, जोहान कार्ल फ्रेडरिक गॉस ने 1809 में अपनी पद्धति का पहला उल्लेख किया। कम से कम वर्ग विधि के लिए कई मापदंडों के लिए हेसियन मैट्रिक्स की गणना में बहुत समय लग सकता है। अब हम मान सकते हैं कि गॉस-न्यूटन एल्गोरिथ्म गणनाओं को सरल बनाने के लिए जैकोबी मैट्रिक्स के माध्यम से हेसियन मैट्रिक्स के सन्निकटन का उपयोग करता है। लेकिन इतिहास के दृष्टिकोण से, ऐसा नहीं है: लुडविग ओटो हेसे (जिन्होंने उनके नाम पर मैट्रिक्स का विकास किया) 1811 में पैदा हुआ था - एल्गोरिथम के पहले उल्लेख के 2 साल बाद। और कार्ल गुस्ताव जैकोबी 5 साल का था।

गॉस-न्यूटन एल्गोरिथ्म नुकसान फ़ंक्शन के साथ काम नहीं करता है। यह अवशिष्ट कार्य के साथ काम करता है $आर (पी)$ । यह फ़ंक्शन मापदंडों का एक इनपुट वेक्टर लेता है $पी$ और एक अवशिष्ट वेक्टर देता है । हमारे मामले में, वेक्टर $पी$ 2 घटक (पैरामीटर) होते हैं $एक$ और $ब$ रोसेनब्रॉक फ़ंक्शंस), और अवशिष्ट वेक्टर से $एम$ घटक (प्रयोगों की संख्या के अनुसार)। वेक्टर तर्क का वेक्टर फ़ंक्शन प्राप्त किया जाता है। इसका व्युत्पन्न:

जैकोबी मैट्रिक्स (वेक्टर दर्ज - वेक्टर जारी)

एक फ़ंक्शन पर विचार करें जो एक वेक्टर को इनपुट के रूप में लेता है और एक वेक्टर भी पैदा करता है: $f: \ mathbb {R} ^ {N} \ rightarrow \ mathbb {R} ^ {M}$ । यौगिक $च$ बिंदु पर $x$ अब आकार है $N \ गुना M$ , जिसे जैकोबी मैट्रिक्स कहा जाता है , और इसमें आंशिक डेरिवेटिव के सभी संयोजन शामिल हैं:

$\ boldsymbol {J} y_ {x} = \ start {pmatrix} \ frac {\ आंशिक y_ {1}} {\ आंशिक x_ {1}} & \ cdots & \ frac {\ आंशिक y {1}} {\ _ \ _ आंशिक x_ {N}} \\ \ vdots & \ ddots & \ vdots \\ \ frac {\ आंशिक y_ {M}} {\ आंशिक x_ {1}} & \ cdots & \ frac {आंशिक y_ {M}} {आंशिक x_ {N}} \ end {pmatrix}$

आप देख सकते हैं कि जैकोबी मैट्रिक्स की पंक्तियाँ घटकों के ग्रेडिएंट हैं $य$ । तत्त्व $(i, j)$ मैट्रिक्स $\ frac {\ आंशिक y} {\ आंशिक x}$ के बराबर है $\ frac {\ आंशिक y_ {i}} {\ आंशिक x_ {j}}$ और हमें बताता है कि कितना परिवर्तन होगा $y_ {i}$ जब बदल रहा हो $x_ {j}$ एक छोटे से मूल्य पर। पिछले मामलों की तरह, आप लिख सकते हैं:

$x \ rightarrow x + \ Delta x \ Rightarrow y \ rightarrow \ लगभग y + \ boldsymbol {J} y_ {x} \ Delta x$

यहां $\ _ सुनहरा {J} y_ {x}$ मैट्रिक्स $N \ गुना M$ , और $\ Delta x$ आकार वेक्टर $एन$ इस प्रकार उत्पाद $\ boldsymbol {J} y_ {x} \ Delta x$ वेक्टर द्वारा मैट्रिक्स का उत्पाद है, जिसके परिणामस्वरूप आकार का एक वेक्टर होता है $एम$ ।

वर्णों की बहुतायत में भ्रमित न होने के लिए, हम यह मान लेते हैं $\ boldsymbol {J} _ {r}$ - वर्तमान बिंदु पर अवशिष्ट कार्यों के जैकोबी मैट्रिक्स $\ boldsymbol {p}$ । तब गॉस-न्यूटन एल्गोरिथम को निम्नानुसार लिखा जा सकता है:

$\ boldsymbol {p} \ rightarrow \ boldsymbol {p} - [\ boldsymbol {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r}] ^ {- 1 = \ boldsymbol {J} _ {r} } ^ \ intercal r (\ boldsymbol {p})$

फॉर्म में रिकॉर्डिंग पूरी तरह से न्यूटन की विधि की रिकॉर्डिंग के साथ मेल खाती है। केवल हेसियन मैट्रिक्स के बजाय उपयोग किया जाता है $\ _ सुनहरा {J} _ {r} ^ \ intercal \ boldsymbol {J} _ {r$ ग्रेडिएंट के बजाय $\ boldsymbol {J} _ {r} ^ \ intercal r (\ boldsymbol {p})$ । अगला, हम देखेंगे कि इस तरह के सन्निकटन का उपयोग क्यों किया जा सकता है। इस बीच, चलो TensorFlow पर कार्यान्वयन के लिए आगे बढ़ें:

 #  ,  TensorFlow     , #   ,        #  .  ,   : # 1)       tf.unstack(r) # 2)      tf.gradients(r_i, p) # 3)       tf.stack #      ,     #       j = tf.stack([tf.gradients(r_i, p)[0] for r_i in tf.unstack(r)]) jT = tf.transpose(j) #     - r_col = tf.expand_dims(r, -1) #      hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r_col) # ,      dp = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) #  -  - dp = tf.squeeze(dp) #  p  dp    ng = opt.apply_gradients([(dp, p)]) #   ,    40000  session.run(tf.global_variables_initializer()) train(1e-10, 40000, loss, ng, feed_dict)

 [Out]: step: 1, current loss: 3868.2291666666665 step: 2, current loss: 14.653025157673625 step: 4, current loss: 4.3918079172783016e-07 ENDED ON STEP: 4, FINAL LOSS: 3.374364957618591e-17 PARAMETERS: [2.5 2.5]

पर्याप्त 4 कदम। न्यूटन की विधि की तुलना में कम है।

जैसा कि कोड से देखा जा सकता है, नुकसान फ़ंक्शन का उपयोग अनुकूलन में नहीं किया जाता है, केवल मानदंड और लॉगिंग मानदंड के लिए किया जाता है। अनुकूलन एल्गोरिथ्म कैसे जानता है कि किस फ़ंक्शन को कम करना है? जवाब आश्चर्य की बात है: कोई रास्ता नहीं! गॉस-न्यूटन न्यूनतम मतलब चुकता त्रुटि है ।

लेख के गणितीय भाग को ठीक करें

हमने अपनी जरूरत का सारा गणित दोहराया। आइए इसे केवल प्रोग्रामिंग और TensorFlow पर आगे ध्यान केंद्रित करने के लिए थोड़ा ठीक करें। गणितीय क्रियाओं के अनुक्रम का पता लगाने के लिए आपको एक पेंसिल की आवश्यकता हो सकती है।

एक मॉडल है $y = f (x, p)$ जहाँ $x$ - वेक्टर $पी$ - आयाम मापदंडों के वेक्टर $एन$ , और $य$ - स्केलर। प्राप्त प्रयोगों से $एम$ अंक $(x_ {1}, y_ {1}), ..., (x_ {m}, y_ {m})$ ( डेटा जोड़े )। वेक्टर अवशिष्ट फ़ंक्शन केवल पैरामीटर वेक्टर पर निर्भर करता है: $r (p) = (r_ {1} (p), ... r_ {m} (p))$ जहाँ $r_ {k} (p) = y_ {k} - \ widehat {y_ {k}} = y_ {k} - f (x_ {k}, p)$ । , $p$ , $x_{k}, y_{k}$ ? , $x_{k}, y_{k}$ , .

$p$ , ( sum of squared error — sse residual sum-of-squares — rss ) . mse sse , $एम$ । . :

$loss(p) = r_{1}^2(p) + \cdots + r_{m}^2(p) = \sum_{k=1}^{m} r_{k}^2(p)$

$p$ $(p)$ ।

, . — . — , $r^2$ $2r \frac{\partial r}{\partial p}$ । :

$\nabla_{p}loss = (\sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{1}}, \cdots, \sum_{k=1}^{m}2r_{k}\frac{\partial r_{k}}{\partial p_{n}})$

. :

$[\boldsymbol{H}loss_{p}]_{ij} = \frac{\partial^2 loss}{\partial p_{i} \partial p_{j}} = \sum_{k=1}^{m}(2\frac{\partial r_{k}}{\partial p_{i}}\frac{\partial r_{k}}{\partial p_{j}} + 2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}})$

. , , ${(uv)}'={u}'v+u{v}'$ ।
बहुत बढ़िया! .

, , , — $2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$ । , , $r_{k}$ , . — . , ? -.

$\boldsymbol{J}_{r} = \begin{pmatrix} \frac{\partial r_{1}}{\partial p_{1}} & \cdots & \frac{\partial r_{1}}{\partial p_{n}}\\ \vdots & \ddots & \vdots \\ \frac{\partial r_{m}}{\partial p_{1}} & \cdots & \frac{\partial p_{m}}{\partial p_{n}} \end{pmatrix}$

, , . ध्यान दें:

$2\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r} \approx \boldsymbol{H}loss_{p}$

"" . ( ). , — $2r_{k}\frac{\partial^2 r_{k}}{\partial p_{i}\partial p_{j}}$ , .
( ):

$2\boldsymbol{J}_{r}^\intercal r = \nabla_{p}loss$

, , - — , mse .

. , , . $एम$ $(x_{1}, y_{1}), ..., (x_{m}, y_{m})$ , $y = rosenbrock(x, p)$ । $p$ , .

, : " . - ! ". , , , ( supervised learning ). , . : ( training set ) — ; — ( prediction model ) ; — , .

( multi-layer perceptron neural network mlp ). , , :

( starting values ) . Xavier'a, .
( overfitting ). — . , . — .
( scaling of the input ). , .

9 . 500:

 #    def get_random_rosenbrock_data_points(m): result = np.zeros((m, 3)) result[:, 0] = np.random.uniform(-2, 2, m) result[:, 1] = np.random.uniform(-2, 2, m) result[:, 2] = rosenbrock(result[:, 0], result[:, 1], 2.5, 2.5) return result m = 500 data_points = get_random_rosenbrock_data_points(m) # overfitting   ,      validation_data_points = get_random_rosenbrock_data_points(m)

500 . — ( learner ), ( outcome measurement ) ( features ) .

( network diagram ). MatLab:

( input ). $W$ ( weights ) 2x10, $b$ ( bias ) 10, ( activation ). () ( hidden layer ) 10 . , , ( output ).

, , ( $tanh$ ):

$\begin{matrix} h_{1} = tanh(xW_{1} + b_{1})\\ \widehat{y} = h_{1}W_{2} + b_{2} \end{matrix}$

$h_1 = tanh(\begin{bmatrix} x_1 & x_2 \end{bmatrix}\begin{bmatrix} w^{(1)}_{1,1} & \cdots& w^{(1)}_{1,10} \\ w^{(1)}_{2,1} &\cdots& w^{(1)}_{2,10} \end{bmatrix} + \begin{bmatrix} b^{(1)}_1 & \cdots & b^{(1)}_{10} \end{bmatrix}) \\ \widehat{y} = \begin{bmatrix}h^{(1)}_1 & \cdots & h^{(1)}_{10}\end{bmatrix} \begin{bmatrix} w^{(2)}_{1,1} \\ \vdots \\ w^{(2)}_{1,10} \\ \end{bmatrix} + b_2$

. $W_{1}$ "" $h_{1}$ , - $W_{2}$ । 41 . , .

$m \times 2$ , . - $\widehat{y}$ से $एम$ :

 #     10 "" n_hidden = 10 #      Xavier'a initializer = tf.contrib.layers.xavier_initializer() #    x = tf.placeholder(tf.float64, shape=[m, 2]) y = tf.placeholder(tf.float64, shape=[m, 1]) #         W1 = tf.Variable(initializer([2, n_hidden], dtype=tf.float64)) b1 = tf.Variable(initializer([1, n_hidden], dtype=tf.float64)) #   ,  tanh   h1 = tf.nn.tanh(tf.matmul(x, W1) + b1) #        W2 = tf.Variable(initializer([n_hidden, 1], dtype=tf.float64)) b2 = tf.Variable(initializer([1], dtype=tf.float64)) #   y_hat = tf.matmul(h1, W2) + b2 #  r = y - y_hat #   mse     loss = tf.reduce_mean(tf.square(r)) #      placeholder feed_dict = {x: data_points[:,0:2], y: data_points[:,2:3]} validation_feed_dict = {x: validation_data_points[:,0:2], y: validation_data_points[:,2:3]}

Adam

Adam $rosenbrock$ । mse :

 #    adm = tf.train.AdamOptimizer(1e-2).minimize(loss) session.run(tf.global_variables_initializer()) #   ,    40000  train(1e-10, 40000, loss, adm, feed_dict) print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))

 [Out]: step: 1, current loss: 671.4242576535694 [...] ENDED ON STEP: 40000, FINAL LOSS: 0.22862158574440725 VALIDATION LOSS: 0.29000289644978866

. : , , .

$rosenbrock$ 2 . :

. 9 , 500. .
. - $p$ , .

 #      y   x def jacobian(y, x): loop_vars = [ tf.constant(0, tf.int32), tf.TensorArray(tf.float64, size=m), ] #  -   #      _, jacobian = tf.while_loop( lambda i, _: i < m, #           #   (-),   x     lambda i, res: (i+1, res.write(i, tf.reshape(tf.gradients(y[i], x), (-1,)))), loop_vars) #       return jacobian.stack() #       r_flat = tf.squeeze(r) #        #       parms = [W1, b1, W2, b2] parms_sizes = [tf.size(p) for p in parms] j = tf.concat([jacobian(r_flat, p) for p in parms], 1) jT = tf.transpose(j) #           hess_approx = tf.matmul(jT, j) grad_approx = tf.matmul(jT, r)

$\boldsymbol{J}r_{p}$ . , 4 $W_1, b_1, W_2, b_2$ । 4 $\boldsymbol{J}r_{W_1}, \boldsymbol{J}r_{b_1}, \boldsymbol{J}r_{W_2}, \boldsymbol{J}r_{b_2}$ tf.concat .

. tf.while_loop , $r_i$ , , stack .

$r_i$ $W_1$ : $\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} \\ \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$ । tf.reshape (-1,) $\begin{bmatrix} \frac{\partial r_i}{\partial w^{(1)}_{1,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{1,10}} & \frac{\partial r_i}{\partial w^{(1)}_{2,1}} & \cdots& \frac{\partial r_i}{\partial w^{(1)}_{2,10}} \end{bmatrix}$ ।

. - . — TensorFlow . — - - $W_1, b_1, W_2, b_2$ । -. Levenberg-Marquardt Jupyter Notebook rosenbrock_train.py . , TensorFlow . - , ( ) , , .

-

hess_approx grad_approx -. $rosenbrock$ , . :

: $\Delta \boldsymbol{p} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} & \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} & \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} & \Delta b_2\end{bmatrix}$
:
$\Delta W_{1} = \begin{bmatrix}\Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$ । $\Delta b_{1} = \begin{bmatrix} \Delta b^{(1)}_1 & \cdots & \Delta b^{(1)}_{10} \end{bmatrix}$ । $\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} & \cdots & \Delta w^{(2)}_{1,10} \end{bmatrix}$ । $\Delta b_{2} = \begin{bmatrix} \Delta b_2\end{bmatrix}$ ।
, :
$\Delta W_{1} = \begin{bmatrix} \Delta w^{(1)}_{1,1} & \cdots & \Delta w^{(1)}_{1,10} \\ \Delta w^{(1)}_{2,1} &\cdots & \Delta w^{(1)}_{2,10} \end{bmatrix}$ । $\Delta W_{2} = \begin{bmatrix} \Delta w^{(2)}_{1,1} \\ \vdots \\ \Delta w^{(2)}_{1,10} \\ \end{bmatrix}$
.

 # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       gn = opt.apply_gradients(zip(dps, parms)) #   session.run(tf.global_variables_initializer()) train(1e-10, 100, loss, gn, feed_dict)

 [Out]: step: 1, current loss: 548.8468777701685 step: 2, current loss: 49648941.340197295 InvalidArgumentError: Input is not invertible.

- . , . - , .

, .

-

. Matlab trainlm . . MathWorks.

- : $\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$ । - :

$\boldsymbol{p} \rightarrow \boldsymbol{p}-[\boldsymbol{J}_{r}^\intercal\boldsymbol{J}_{r}+\mu \boldsymbol{I}]^{-1}\boldsymbol{J}_{r}^\intercal r(\boldsymbol{p})$

$\ _मु$ $मैं$ $एन$ ( ). $\ _मु$ , -. , . , LM -.

 mu = tf.placeholder(tf.float64, shape=[1]) n = tf.add_n(parms_sizes) I = tf.eye(n, dtype=tf.float64) # 1.     dp_flat = tf.matmul(tf.linalg.inv(hess_approx + tf.multiply(mu, I)), grad_approx) # 2.     dps = tf.split(dp_flat, parms_sizes, 0) # 3.     for i in range(len(dps)): dps[i] = tf.reshape(dps[i], parms[i].shape) # 4.  :       lm = opt.apply_gradients(zip(dps, parms))

$\ _मु$ ? LM - . , . , $\ _मु$ , . — , mse . , :

 #       store = [tf.Variable(tf.zeros(p.shape, dtype=tf.float64)) for p in parms] #  TensorFlow       save_parms = [tf.assign(s, p) for s, p in zip(store, parms)] restore_parms = [tf.assign(p, s) for s, p in zip(store, parms)] #   mu    3. feed_dict[mu] = np.array([3.]) step = 0 session.run(tf.global_variables_initializer()) #    mse current_loss = session.run(loss, feed_dict) #    100   while current_loss > 1e-10 and step < 100: step += 1 #  1, 2, 4...   if math.log(step, 2).is_integer(): print(f'step: {step}, mu: {feed_dict[mu][0]} current loss: {current_loss}') #    session.run(save_parms) # ,     mse while True: #    session.run(lm, feed_dict) new_loss = session.run(loss, feed_dict) if new_loss > current_loss: #  -  mu  10     feed_dict[mu] *= 10 session.run(restore_parms) else: #  -  mu  10     feed_dict[mu] /= 10 current_loss = new_loss break print(f'ENDED ON STEP: {step}, FINAL LOSS: {current_loss}') print('VALIDATION LOSS: '+str(session.run(loss, validation_feed_dict)))

 [Out]: step: 1, mu: 3.0 current loss: 692.6211687622557 [...] ENDED ON STEP: 100, FINAL LOSS: 0.012346989371823602 VALIDATION LOSS: 0.01859463694102034

100 LM mse 10 , 40 .

. , . , rosenbrock_train.py .

2D . . . , " " ( curse of dimentionality , Bellman, 1961). . .

$f(\boldsymbol{x}) = \sum_{i=1}^{N-1}\left [ 100(x_{i+1} - x_{i}^2)^2 + (1-x_{i})^2 \right ], \boldsymbol{x}=[x_1 \cdots x_{N}]\in \mathbb{R}^N$

rosenbrock_train.py get_rand_rosenbrock_points .

-

- : " ! 4 , 300! ". , ( ) -. , , . - . . : ? , . . , - :

10 000 6D .
3 12, 10, 8 (311 ).
.
3.5 .

. - 2 . LM . 20 .

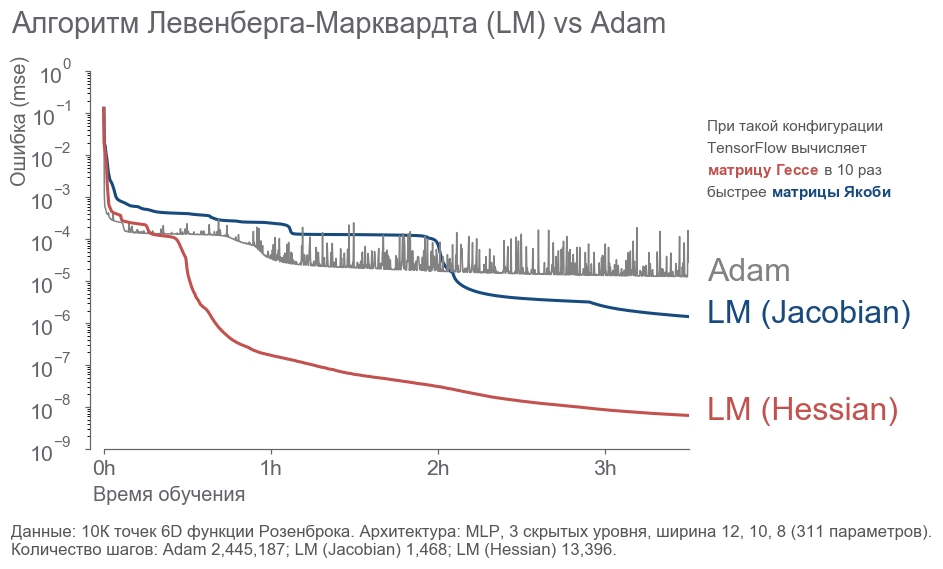
rosenbrock_train.py . . , .

निष्कर्ष

, . " ", , . , . , 273 . - , .

, :

.
( ) -:
[1] Petros Drineas, Ravi Kannan, and Michael W. Mahoney. 2006. Fast Monte Carlo Algorithms for Matrices I: Approximating Matrix Multiplication. SIAM J. Comput. 36, 1 (July 2006), 132-157. DOI= http://dx.doi.org/10.1137/S0097539704442684
[2] Adelman, M., & Silberstein, M. (2018). Faster Neural Network Training with Approximate Tensor Operations. CoRR, abs/1805.08079.

, - . , . "".

TensorFlow पर तंत्रिका नेटवर्क के अनुकूलन के लिए लेवेनबर्ग-मार्क्वर्ट एल्गोरिथ्म का कार्यान्वयन