मैंने एक लंबे समय के लिए तैयार किया और सामग्री एकत्र की, मुझे उम्मीद है कि इस बार यह बेहतर निकला। मैं इस लेख को सीमाओं के साथ गणितीय अनुकूलन समस्याओं को हल करने के लिए बुनियादी तरीकों के लिए समर्पित करता हूं, इसलिए यदि आपने सुना कि सिंप्लेक्स विधि कुछ
बहुत महत्वपूर्ण विधि है, लेकिन फिर भी यह नहीं जानते कि यह क्या करता है, तो यह लेख शायद आपकी मदद करेगा।
PS आलेख में मैक्रो संपादक द्वारा जोड़े गए गणितीय सूत्र शामिल हैं। वे कहते हैं कि कभी-कभी वे प्रदर्शित नहीं होते हैं। जीआईएफ प्रारूप में कई एनिमेशन भी हैं।
प्रस्तावना
गणितीय अनुकूलन की समस्या फ़ॉर्म की समस्या है "सेट में खोजें
mathcalK तत्व
x∗ ऐसे सभी के लिए
x से
mathcalK प्रदर्शन
f(x∗) leqf(x) ”, वैज्ञानिक साहित्य में कौन सा ऐसा कुछ लिखे जाने की संभावना है
\ start {array} {rl} \ mbox {छोटा} & f (x) \\ \ mbox {प्रदान किया गया} और x \ in \ mathcal {K}। \ अंत {सरणी}
\ start {array} {rl} \ mbox {छोटा} & f (x) \\ \ mbox {प्रदान किया गया} और x \ in \ mathcal {K}। \ अंत {सरणी}
ऐतिहासिक रूप से, लोकप्रिय विधियां जैसे कि ढाल वंश या न्यूटन की विधि केवल रैखिक स्थानों में काम करती हैं (और अधिमानतः सरल वाले, उदाहरण के लिए)
mathbbRn )। व्यवहार में, अक्सर ऐसी समस्याएं होती हैं जहां आपको रैखिक स्थान में न्यूनतम नहीं खोजने की आवश्यकता होती है। उदाहरण के लिए, आपको ऐसे वैक्टर पर कुछ फ़ंक्शन को कम से कम खोजने की आवश्यकता है
x=(x1, ldots,xn) जिसके लिए
xi geq0 , यह इस तथ्य के कारण हो सकता है कि
xi किसी भी ऑब्जेक्ट की लंबाई को निरूपित करें। या उदाहरण के लिए, यदि
x एक बिंदु के निर्देशांक का प्रतिनिधित्व करते हैं जो इससे अधिक नहीं होना चाहिए
आर से
य , टी ई
x−y | leqr । ऐसी समस्याओं के लिए, ढाल वंश या न्यूटन विधि अब सीधे लागू नहीं होती है। यह पता चला कि अनुकूलन समस्याओं का एक बहुत बड़ा वर्ग आसानी से "प्रतिबंध" द्वारा कवर किया गया है, उन लोगों के समान जो मैंने ऊपर वर्णित किया था। दूसरे शब्दों में, सेट का प्रतिनिधित्व करना सुविधाजनक है
mathcalK समानता और असमानताओं की एक प्रणाली के रूप में
startarraylgi(x) leq0, 1 leqi leqm,hi(x)=0, 1 leqi leqk। अंतसरणी
फ़ॉर्म की जगह पर न्यूनतमकरण की समस्याएं
mathbbRn इस प्रकार उन्होंने मनमाने ढंग से उन्हें "असंबंधित समस्या" कहना शुरू कर दिया, और समानता और असमानताओं के सेट द्वारा परिभाषित समस्याओं पर - "विवश समस्याएं"।
तकनीकी रूप से, बिल्कुल कोई भी भीड़
mathcalK संकेतक- फंक्शन का उपयोग करके एकल समानता या असमानता के रूप में प्रतिनिधित्व किया जा सकता है, जिसे इस रूप में परिभाषित किया गया है
I_ \ mathcal {K} (x) = \ start {case} 0, & x \ notin \ mathcal {K} \\ 1, & x \ in \ mathcal {K}, \ end {केस}
हालांकि, इस तरह के फ़ंक्शन में विभिन्न उपयोगी गुण (उत्तलता, भिन्नता, आदि) नहीं होते हैं। हालांकि, कोई अक्सर कल्पना कर सकता है
mathcalK कई समानताएं और असमानताओं के रूप में, जिनमें से प्रत्येक में ऐसे गुण हैं। मामले के तहत मूल सिद्धांत को संक्षेप में प्रस्तुत किया गया है
\ start {array} {rl} \ mbox {छोटा} & f (x) \\ \ mbox {प्रदान किया गया} और g_i (x) \ leq 0, ~ 1 \ leq i \ leq m \\ & Ax = b , \ अंत {सरणी}
जहाँ
च,gi - उत्तल (लेकिन आवश्यक रूप से भिन्न नहीं) कार्य,
ए - मैट्रिक्स। यह प्रदर्शित करने के लिए कि तरीके कैसे काम करते हैं, मैं दो उदाहरणों का उपयोग करूंगा:
- रैखिक प्रोग्रामिंग कार्य
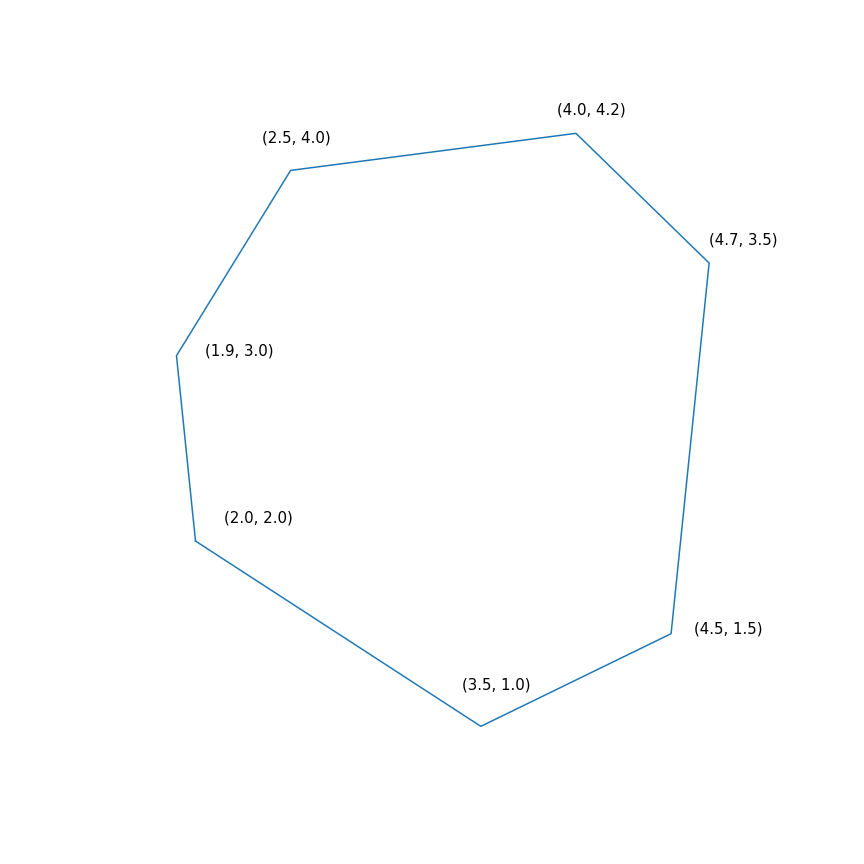
$$ प्रदर्शन $ $ \ _ {आरंभ}} आरएल} \ mbox {न्यूनतम} & -2 & x ~~~ - & y \\ \ mbox {प्रदान} & -1.0 & ~ x -0.1 & ~ y \ leq -1.0 \ \ & -1.0 & ~ x + ~ 0.6 & ~ y \ leq -1.0 \\ & -0.2 & ~ x + ~ 1.5 & ~ y \ leq -0.2 \\ & ~ 0.7 & ~ x + ~ 0.7 & ~ y \ leq 0.7 \\ & ~ 2.0 & ~ x -0.2 & ~ y \ leq 2.0 \\ & ~ 0.5 & ~ x -1.0 & ~ y \ leq 0.5 \\ & -1.0 & ~ x -1.5 & ~ y \ leq - 1.0 \\ \ end {सरणी} $ $ प्रदर्शन $ $
संक्षेप में, इस समस्या को दिशा (2, 1) में बहुभुज के सबसे दूर के बिंदु को खोजने में शामिल है, समस्या का समाधान बिंदु (4.7, 3.5) है - बहुभुज में सबसे "सही" है। लेकिन बहुभुज ही
- एक द्विघात अवरोध के साथ एक द्विघात कार्य का न्यूनतमकरण
\ start {सरणी} {rl} \ mbox {छोटा} और 0.7 (x - y) ^ 2 + 0.1 (x + y) ^ 2 \\ \ mbox {प्रदान}} & (x-4) ^ 2 + ( y-6) ^ 2 \ leq 9 \ end {सरणी}
सिंप्लेक्स विधि
सभी तरीकों में से जो मैं इस समीक्षा के साथ कवर करता हूं, सरल विधि शायद सबसे प्रसिद्ध है। विधि विशेष रूप से लीनियर प्रोग्रामिंग के लिए विकसित की गई थी और प्रस्तुत में से केवल एक ही चरण की परिमित संख्या में सटीक समाधान प्राप्त करता है (बशर्ते कि गणना के लिए सटीक अंकगणित का उपयोग किया जाता है, व्यवहार में यह आमतौर पर मामला नहीं है, लेकिन सिद्धांत रूप में यह संभव है)। एक सरल विधि के विचार में दो भाग होते हैं:
- रैखिक असमानता और समानता की प्रणालियाँ बहुआयामी उत्तल बहुभुज (बहुवचन) को परिभाषित करती हैं। एक आयामी मामले में, यह एक बिंदु, किरण या खंड है, दो आयामी मामले में, एक उत्तल बहुभुज, तीन आयामी मामले में, एक उत्तल बहुभुज। लीनियर फ़ंक्शन को कम से कम करना एक निश्चित दिशा में "सबसे दूर" बिंदु ढूंढना है। मुझे लगता है कि अंतर्ज्ञान को सुझाव देना चाहिए कि यह बहुत दूर का बिंदु एक निश्चित शिखर होना चाहिए, और यह वास्तव में ऐसा है। सामान्य तौर पर, एक प्रणाली से एम में असमानताएँ एन -डिमेटिक स्पेस एक वर्टेक्स एक ऐसा बिंदु है जो सिस्टम को संतुष्ट करता है एन इनमें से असमानताएं समानता में बदल जाती हैं (बशर्ते कि विषमताओं में कोई समानता न हो)। हमेशा ऐसे बिंदुओं की एक सीमित संख्या होती है, हालांकि उनमें से बहुत कुछ हो सकता है।
- अब हमारे पास बिंदुओं का एक सीमित सेट है, आम तौर पर बोलना, आप बस उन्हें चुन सकते हैं और छांट सकते हैं, अर्थात्, कुछ ऐसा करें: प्रत्येक सबसेट के लिए एन असमानताएं, चुने हुए असमानताओं पर संकलित रैखिक समीकरणों की प्रणाली को हल करती हैं, यह सत्यापित करें कि समाधान असमानताओं की मूल प्रणाली को फिट करता है और ऐसे अन्य बिंदुओं के साथ तुलना करता है। यह एक काफी सरल अक्षम लेकिन काम करने का तरीका है। सिम्प्लेक्स विधि, पुनरावृति के बजाय, किनारों के साथ ऊपर से ऊपर की ओर चलती है ताकि उद्देश्य फ़ंक्शन के मूल्यों में सुधार हो। यह पता चला है कि यदि किसी शीर्ष पर "पड़ोसी" नहीं है जिसमें फ़ंक्शन के मान बेहतर हैं, तो यह इष्टतम है।
सिंप्लेक्स विधि पुनरावृत्ति है, अर्थात्, यह क्रमिक रूप से समाधान में थोड़ा सुधार करता है। इस तरह के तरीकों के लिए, आपको कहीं शुरू करने की आवश्यकता है, सामान्य स्थिति में यह एक सहायक समस्या को हल करके किया जाता है
\ start {array} {rl} \ mbox {न्यूनतम} & s \\ \ mbox {प्रदान} & g_i (x) \ leq s, ~ 1 \ leq i \ leq m \\ \ end {array}
अगर इस समस्या को हल करने के लिए
x∗,s∗ ऐसा है
s∗ leq0 फिर निष्पादित किया गया
gi(x∗) leqs leq0 अन्यथा, मूल समस्या आम तौर पर एक खाली सेट पर दी जाती है। सहायक समस्या को हल करने के लिए, आप सिम्प्लेक्स विधि का भी उपयोग कर सकते हैं, लेकिन प्रारंभिक बिंदु लिया जा सकता है
s= maxigi(x) मनमानी के साथ
x । प्रारंभिक बिंदु को खोजने को मनमाने ढंग से विधि का पहला चरण कहा जा सकता है, मूल समस्या के समाधान को खोजने को मनमाने ढंग से विधि का दूसरा चरण कहा जा सकता है।
द्वि-चरण सिंप्लेक्स विधि का प्रक्षेपवक्रप्रक्षेपवक्र scipy.optimize.linprog का उपयोग करके उत्पन्न किया गया था।
प्रोजेक्टिव ग्रेडिएंट डिसेंट
धीरे-धीरे वंश के बारे में, मैंने हाल ही में एक अलग
लेख लिखा है जिसमें मैंने इस पद्धति का संक्षिप्त वर्णन भी किया है। अब यह विधि काफी जीवंत है, लेकिन एक अधिक सामान्य
समीपस्थ ढाल वंश के हिस्से के रूप में अध्ययन किया जा रहा है। विधि का बहुत विचार काफी सामान्य है: यदि हम एक उत्तल कार्य के लिए ढाल वंश को लागू करते हैं
च , फिर मापदंडों के सही विकल्प के साथ हमें एक वैश्विक न्यूनतम मिलता है
च । यदि, ढाल वंश के प्रत्येक चरण के बाद, प्राप्त बिंदु को सही किया जाता है, इसके बजाय एक बंद उत्तल सेट पर इसका प्रक्षेपण होता है।
mathcalK , तब परिणामस्वरूप हमें न्यूनतम कार्य मिलता है
च पर
mathcalK । खैर, या अधिक औपचारिक रूप से, प्रक्षेपवक्र ढाल वंशज एक एल्गोरिथ्म है जो क्रमिक रूप से गणना करता है
केसxk+1=yk− Alphak nablaf(yk)yk+1=P mathcalK(x++1), अंतमामलों
जहाँ
P mathcalK(x)= mboxargminy in mathcalK |x−y ||
अंतिम समानता सेट पर प्रक्षेपण के मानक ऑपरेटर को परिभाषित करती है, वास्तव में यह एक फ़ंक्शन है, जो बिंदु के अनुसार है
x सेट के निकटतम बिंदु की गणना करता है
mathcalK । दूरी की भूमिका यहां निभाई जाती है
| ldots | , यह ध्यान देने योग्य है कि यहां किसी भी
मानदंड का उपयोग किया जा सकता है, हालांकि, विभिन्न मानदंडों के साथ अनुमान भिन्न हो सकते हैं!
व्यवहार में, प्रोजेक्टिव ग्रेडिएंट डीसेंट का उपयोग केवल विशेष मामलों में किया जाता है। इसकी मुख्य समस्या यह है कि प्रक्षेपण की गणना मूल एक की तुलना में अधिक कठिन हो सकती है, और इसे कई बार गणना करने की आवश्यकता होती है। सबसे आम मामला जिसके लिए प्रोजेक्टिव ग्रेडिएंट डीसेंट का उपयोग करना सुविधाजनक है, वह है "बॉक्स प्रतिबंध", जिसका स्वरूप है
elli leqxi leqri, 1 leqi leqn।
इस मामले में, प्रक्षेपण की गणना बहुत सरलता से की जाती है, प्रत्येक समन्वय के लिए यह निकलता है
]]। अंतमामलों
रैखिक प्रोग्रामिंग समस्याओं के लिए प्रक्षेप्य ढाल वंश का उपयोग पूरी तरह से व्यर्थ है, हालांकि, यदि आप ऐसा करते हैं, तो यह कुछ इस तरह दिखाई देगा
एक रैखिक प्रोग्रामिंग समस्या के लिए प्रक्षेप्य ढाल वंश प्रक्षेपवक्र और यहाँ दूसरी समस्या के लिए प्रक्षेपवक्र ढाल वंश का प्रक्षेपवक्र है, यदि
और अगर
दीर्घवृत्त विधि
यह विधि उल्लेखनीय है कि यह रैखिक प्रोग्रामिंग समस्याओं के लिए पहला बहुपद एल्गोरिथ्म है; इसे
द्विध्रुवीय विधि का बहुआयामी सामान्यीकरण माना जा सकता है। मैं
हाइपरप्लेन को अलग करने के अधिक सामान्य
तरीके से शुरू करूंगा:
- विधि के प्रत्येक चरण में, कुछ सेट होता है जिसमें समस्या का समाधान होता है।
- प्रत्येक चरण में, एक हाइपरप्लेन का निर्माण किया जाता है, जिसके बाद चयनित हाइपरप्लेन के एक तरफ पड़े हुए सभी बिंदु सेट से हटा दिए जाते हैं, और इस सेट में कुछ नए बिंदु जोड़े जा सकते हैं
अनुकूलन समस्याओं के लिए, "हाइपरप्लेन को अलग करना" का निर्माण उत्तल कार्यों के लिए निम्नलिखित असमानता पर आधारित है
f(y) geqf(x)+ nablaf(x)T(y−x)।
अगर ठीक हो
x , फिर उत्तल कार्य के लिए
च आधा स्थान
nनबलाf(x)T(y−x) geq0 एक बिंदु से कम मूल्य वाले केवल अंक होते हैं
x , जिसका मतलब है कि उन्हें काट दिया जा सकता है, क्योंकि ये बिंदु उस से बेहतर नहीं हैं जो हमने पहले ही पाया है। प्रतिबंधों की समस्याओं के लिए, आप उन बिंदुओं से छुटकारा पा सकते हैं जो प्रतिबंधों में से एक का उल्लंघन करने की गारंटी है।
अलग करने वाले हाइपरप्लेन विधि का सबसे सरल संस्करण केवल बिना किसी बिंदु को जोड़े आधे स्थानों को काट देना है। नतीजतन, हर कदम पर हमारे पास एक निश्चित पॉलीहेड्रॉन होगा। इस पद्धति के साथ समस्या यह है कि पॉलीहेड्रोन के चेहरों की संख्या कदम से कदम तक बढ़ने की संभावना है। इसके अलावा, यह तेजी से बढ़ सकता है।
दीर्घवृत्त विधि वास्तव में प्रत्येक चरण पर एक दीर्घवृत्ताभ संग्रहीत करती है। अधिक सटीक रूप से, हाइपरप्लेन के निर्माण के बाद, न्यूनतम आयतन का एक दीर्घवृत्ताभ निर्मित किया जाता है, जिसमें मूल भागों में से एक होता है। नए बिंदुओं को जोड़कर इसे हासिल किया जा सकता है। एक दीर्घवृत्त हमेशा एक सकारात्मक निश्चित मैट्रिक्स द्वारा परिभाषित किया जा सकता है और एक वेक्टर (एक दीर्घवृत्त का केंद्र) निम्नानुसार होता है
\ mathcal {E} (P, x) = \ {z ~ | ~ (z-x) ^ TP (z-x) \ leq 1 \} |
अर्ध-स्थान और एक और दीर्घवृत्त के चौराहे वाले आयतन में एक न्यूनतम दीर्घवृत्त का निर्माण,
मामूली बोझिल सूत्रों का उपयोग करके किया जा सकता है। दुर्भाग्य से, व्यवहार में, यह विधि अभी भी सिम्पलेक्स विधि या आंतरिक बिंदु विधि जितनी ही अच्छी थी।
लेकिन वास्तव में यह कैसे काम करता है
और के लिए
अंदर की विधि
इस पद्धति का विकास का एक लंबा इतिहास रहा है, पहले आवश्यक शर्तें में से एक उसी समय के आसपास दिखाई दी थी जब सिम्पलेक्स विधि विकसित की गई थी। लेकिन उस समय यह अभी भी प्रभावी नहीं था कि अभ्यास में इस्तेमाल किया जाए। बाद में 1984 में, विधि का एक
प्रकार विशेष रूप से रैखिक प्रोग्रामिंग के लिए विकसित किया गया था, जो सिद्धांत और व्यवहार में दोनों अच्छा था। इसके अलावा, आंतरिक बिंदु विधि केवल सरल विधि के विपरीत, रैखिक प्रोग्रामिंग तक ही सीमित नहीं है, और अब यह प्रतिबंधों के साथ उत्तल अनुकूलन समस्याओं के लिए मुख्य एल्गोरिथ्म है।
विधि का मूल विचार तथाकथित
बाधा फ़ंक्शन के रूप में प्रतिबंधों को जुर्माना के साथ बदलना है। समारोह
F:Int mathcalK rightarrow mathbbR सेट के लिए
बाधा कार्य कहा जाता है
mathcalK अगर
F(x) rightarrow+ infty mboxatx rightarrow आंशिक mathcal।
यहां
Int mathcalK - अंदर
mathcalK ।
आंशिक mathcalK - सीमा
mathcalK । मूल समस्या के बजाय, इस समस्या को हल करने का प्रस्ताव है
mboxद्वारान्यूनतम x varphi(x,t)=tf(x)+F(x)।
एफ और
varphi केवल इनसाइट्स पर दिया गया
mathcalK (वास्तव में, यह वह जगह है जहां से नाम आता है), बाधा की संपत्ति यह सुनिश्चित करती है
varphi कम से कम
x वहाँ। इसके अलावा, और अधिक
टी अधिक से अधिक प्रभाव
च । यथोचित रूप से उचित परिस्थितियों में, यदि आप लक्ष्य बनाते हैं तो आप इसे प्राप्त कर सकते हैं
टी अनंत तक तो न्यूनतम
varphi मूल समस्या के समाधान में जुट जाएगा।
अगर सेट है
mathcalK असमानताओं के एक सेट के रूप में दिया गया
gi(x) leq0, 1 leqi leqm तब बाधा कार्य का मानक विकल्प
लॉगरिदमिक अवरोध हैF(x)=− summi=1 ln(−gi(x))।
न्यूनतम अंक
x∗(t) कार्यों
varphi(x,t) अलग के लिए
टी एक वक्र बनाता है, जिसे आमतौर पर
केंद्रीय मार्ग कहा जाता है, आंतरिक बिंदु विधि, जैसा कि यह था, इस पथ का पालन करने की कोशिश कर रहा है। यह इसी तरह दिखता है
रैखिक प्रोग्रामिंग उदाहरण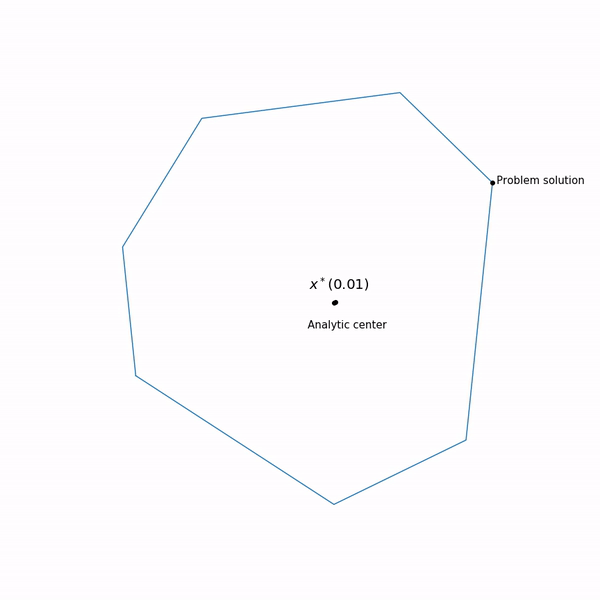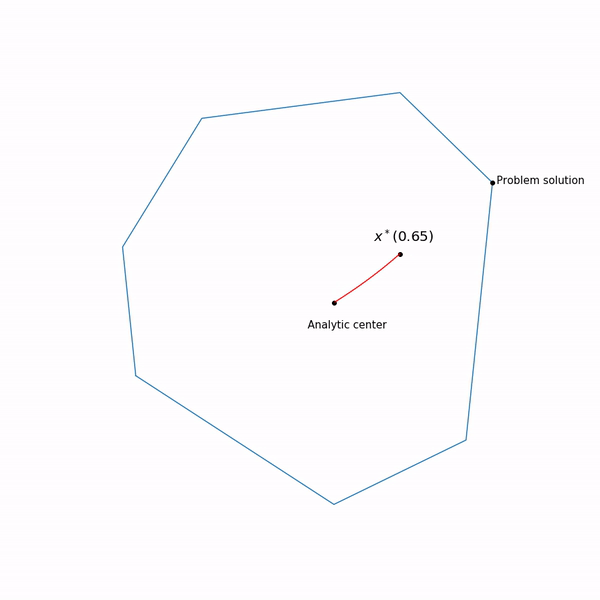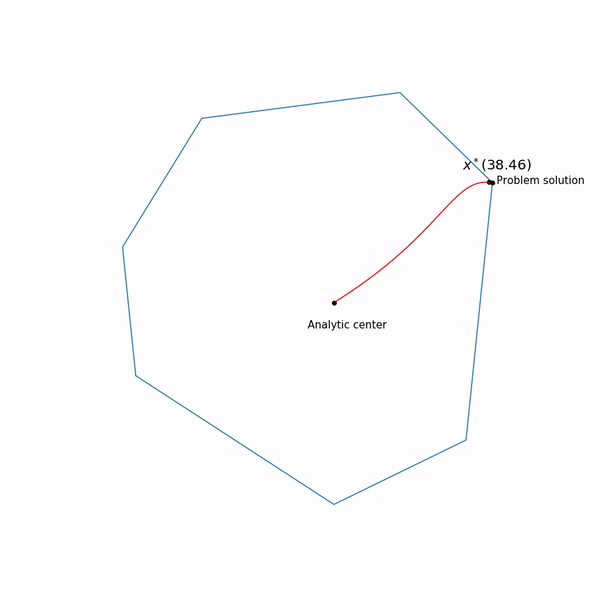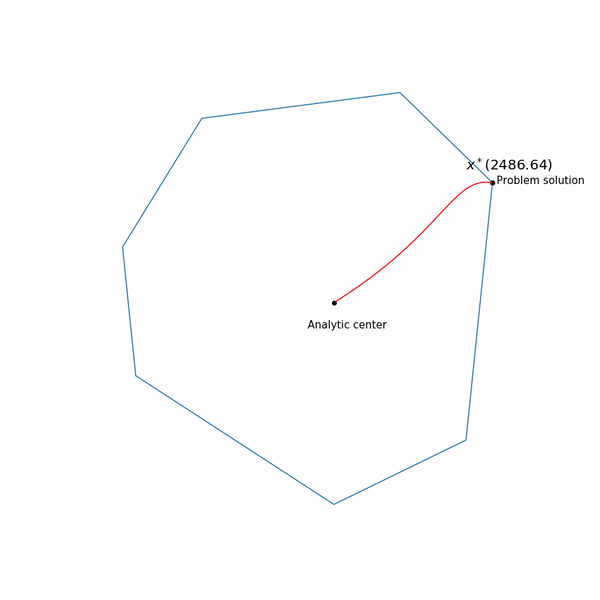 विश्लेषणात्मक केंद्र
विश्लेषणात्मक केंद्र सिर्फ है
x∗(0) अंत में, आंतरिक बिंदु विधि का स्वयं निम्न रूप है
- एक प्रारंभिक सन्निकटन का चयन करें x0 । t0>0
- न्यूटन विधि का उपयोग करके एक नया सन्निकटन चुनें
xk+1=xk−[ nabla2x varphi(xk,tk)]−1 nablax varphi(xk,tk)
- बड़ा करने के लिए क्लिक करें टी
tk+1= अल्फाtk, Alpha>1
न्यूटन विधि का उपयोग यहां बहुत महत्वपूर्ण है: तथ्य यह है कि बाधा फ़ंक्शन के सही विकल्प के साथ, न्यूटन विधि का कदम एक बिंदु उत्पन्न करता है
जो हमारे सेट के अंदर रहता है , हमने प्रयोग किया, यह हमेशा इस रूप में बाहर नहीं देता है। और अंत में, यह आंतरिक बिंदु विधि का प्रक्षेपवक्र कैसा दिखता है
रैखिक प्रोग्रामिंग कार्यउछलती हुई काली बिंदी है
x∗(tk) , यानी। जिस बिंदु पर हम वर्तमान कदम में न्यूटन विधि के कदम से संपर्क करने की कोशिश कर रहे हैं।
द्विघात प्रोग्रामिंग समस्या