🙍🏻 🍕 👬 जूलिया और चरण गतिशील प्रणालियों के चित्र 🆕 🐂 👧🏽

हम युवा और होनहार सामान्य-उद्देश्य वाली भाषा जूलिया में महारत हासिल करना जारी रखते हैं। लेकिन शुरुआत के लिए, हमें आवेदन की बहुत ही संकीर्ण संभावना की आवश्यकता है - भौतिकी की विशिष्ट समस्याओं को हल करने के लिए। यह साधन में महारत हासिल करने के लिए सबसे सुविधाजनक रणनीति है: एक हाथ पाने के लिए, हम दबाने वाली समस्याओं को हल करेंगे, धीरे-धीरे बढ़ती जटिलता और हमारे जीवन को आसान बनाने के तरीके खोजेंगे। संक्षेप में, हम अलग-अलग हल करेंगे और ग्राफ बनाएंगे।

आरंभ करने के लिए, गैडली ग्राफिक्स पैकेज और तुरंत डेवलपर का पूर्ण संस्करण डाउनलोड करें, ताकि यह हमारे जूलिया 1.0.1 के साथ अच्छी तरह से काम करे। हम अपने REPL, JUNO या Jupyter नोटबुक में ड्राइव करते हैं:

using Pkg pkg"add Compose#master" pkg"add Gadfly#master"

सबसे सुविधाजनक विकल्प नहीं है, लेकिन प्लॉटलीज अपडेट के लिए प्रतीक्षा करते समय, आप तुलना के लिए प्रयास कर सकते हैं।

आपको अंतर समीकरणों को हल करने के लिए एक शक्तिशाली उपकरण की भी आवश्यकता है

 ]add DifferentialEquations #

यह सबसे व्यापक और समर्थित पैकेज है जो विभिन्न तरीकों को हल करने के लिए कई तरीके प्रदान करता है। अब चरण पोर्ट्रेट के लिए आगे बढ़ें।

साधारण अंतर समीकरणों के समाधान अक्सर असामान्य रूप में चित्रित करने के लिए अधिक सुविधाजनक होते हैं $y ^ 1 (t), ..., y ^ L (t)$ , और चरण स्थानों में कुल्हाड़ियों के साथ जिनमें से प्रत्येक में पाया गया फ़ंक्शन के मान प्लॉट किए गए हैं। इसके अलावा, तर्क टी केवल पैरामीट्रिक रूप से रेखांकन में शामिल है। दो ओडीई के मामले में, ऐसा ग्राफ - सिस्टम का चरण चित्र - चरण विमान पर एक वक्र है और इसलिए विशेष रूप से दुर्घटना है।

थरथरानवाला

हार्मोनिक थरथरानवाला गतिशीलता $गामा$ समीकरणों की निम्नलिखित प्रणाली द्वारा वर्णित है:

$\ dot {x} = y \\ \ dot {y} = - \ omega ^ 2x + \ gamma y$

और प्रारंभिक स्थितियों की परवाह किए बिना (x0, y0), यह संतुलन की स्थिति, शून्य विक्षेपण कोण और शून्य गति के साथ (0,0) की स्थिति में आता है।

पर $\ Gamma = 0$ समाधान एक शास्त्रीय थरथरानवाला की विशेषता लेता है।

 using DifferentialEquations, Gadfly #     -    function garmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) A = [0 1 -ω^2 γ] syst(u,p,t) = A * u # ODE system u0 = [x0, y0] # start cond-ns tspan = (0.0, 4pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end

कोड का विश्लेषण करते हैं। फ़ंक्शन आवृत्ति और क्षीणन पैरामीटर के मूल्यों को स्वीकार करता है, साथ ही साथ प्रारंभिक शर्तें भी। नेस्टेड सिस्ट () फ़ंक्शन सिस्टम को परिभाषित करता है। इसे चालू करने के लिए, उन्होंने एक-लाइन मैट्रिक्स गुणन का उपयोग किया। बड़ी संख्या में मापदंडों को हल करने वाला समाधान () फ़ंक्शन, समस्या को हल करने के लिए बहुत लचीले ढंग से कॉन्फ़िगर किया गया है, लेकिन हमने केवल समाधान पद्धति का संकेत दिया है - रनगे-कुट्टा 4 ( कई अन्य हैं ), सापेक्ष त्रुटि, और यह तथ्य कि सभी बिंदुओं को बचाया नहीं जाना चाहिए, लेकिन केवल हर चौथे । प्रतिक्रिया मैट्रिक्स को चर सोल में रखा जाता है, इसके अलावा, सोल में कई बार वेक्टर होता है, और इन समय पर सिस्टम को हल करता है। यह सब शांति से प्लॉट्स में खींचा गया है, और गैडली के लिए आपको मैट्रिक्स में उत्तर को और अधिक सुविधाजनक बनाना होगा। हमें समय की आवश्यकता नहीं है, इसलिए हम केवल समाधान लौटाते हैं।

चलो एक चरण चित्र बनाएँ:

 Ans0 = garmosc() plot(x = Ans0[:,1], y = Ans0[:,2])

उच्च-क्रम के कार्यों में, broadcast(f, [1, 2, 3]) हमारे लिए विशेष रूप से उल्लेखनीय है, जो वैकल्पिक रूप से समारोह में सरणी [1, 2, 3] के मूल्यों को प्रतिस्थापित करता है । लघु रिकॉर्ड f.([1, 2, 3]) । यह आवृत्ति, क्षीणन पैरामीटर, प्रारंभिक समन्वय और प्रारंभिक गति को अलग करने के लिए उपयोगी है।

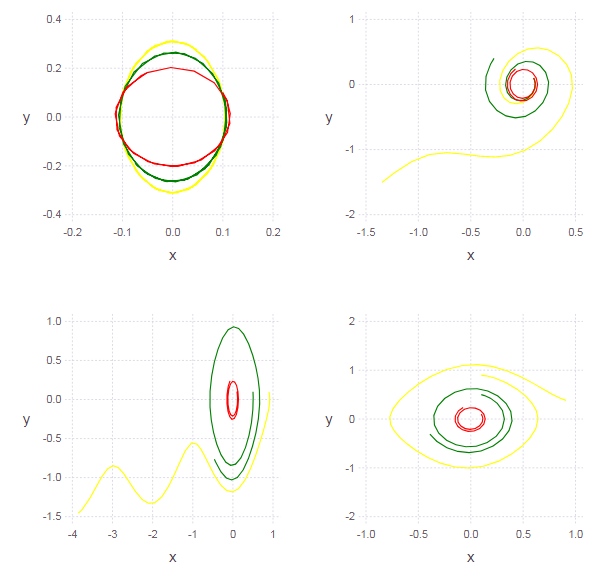
बिगाड़ने वाले के नीचे छिपा हुआ

 L = Array{Any}(undef, 3)#     (  ) clr = ["red" "green" "yellow"] function ploter(Answ) for i = 1:3 L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path, Theme(default_color=clr[i]) ) end p = plot(L[1], L[2], L[3]) end Ans1 = garmosc.( [pi 2pi 3pi] )#  p1 = ploter(Ans1) Ans2 = garmosc.( pi, [0.1 0.3 0.5] )#  p2 = ploter(Ans2) Ans3 = garmosc.( pi, 0.1, [0.2 0.5 0.8] ) p3 = ploter(Ans3) Ans4 = garmosc.( pi, 0.1, 0.1, [0.2 0.5 0.8] ) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) ) #

अब हम छोटे दोलनों पर विचार नहीं करते हैं, लेकिन मनमाने आयाम के दोलनों:

$\ dot {x} = y \\ \ dot {y} = - sin (\ omega x) + \ gamma y$

समाधान का चरण आरेख एक दीर्घवृत्त नहीं है (जो थरथरानवाला की अशुद्धता को इंगित करता है)। कम हम दोलनों के आयाम चुनते हैं (यानी, प्रारंभिक शर्तें), कम अशुद्धता दिखाई देगी (इसलिए, पेंडुलम के छोटे दोलनों को हार्मोनिक माना जा सकता है)।

बिगाड़ने वाले के नीचे छिपा हुआ

 function ungarmosc(ω = pi, γ = 0, x0 = 0.1, y0 = 0.1) function syst(du,u,p,t) du[1] = u[2] du[2] = -sin( ω*u[1] )+γ*u[2] end u0 = [x0, y0] # start cond-ns tspan = (0.0, 2pi) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 4) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end Ans1 = ungarmosc.( [pi 2pi 3pi] ) p1 = ploter(Ans1) Ans2 = ungarmosc.( pi, [0.1 0.4 0.7] ) p2 = ploter(Ans2) Ans3 = ungarmosc.( pi, 0.1, [0.1 0.5 0.9] ) p3 = ploter(Ans3) Ans4 = ungarmosc.( pi, 0.1, 0.1, [0.1 0.5 0.9] ) p4 = ploter(Ans4) vstack( hstack(p1,p2), hstack(p3,p4) )

Brusselator

यह मॉडल एक निश्चित ऑटोकैटलिक रासायनिक प्रतिक्रिया का वर्णन करता है जिसमें प्रसार एक भूमिका निभाता है। मॉडल को 1968 में लेफेब्रे और प्राइगोजिन द्वारा प्रस्तावित किया गया था।

$\ dot {u} _1 = - (\ mu + 1) u_1 + u ^ 2_1u_2 + 1 \\ \ dot {u} _2 = \ mu u_1-u ^ 2_1u_2$

अज्ञात कार्य $u_1 (t), \, u_2 (t)$ एक रासायनिक प्रतिक्रिया के मध्यवर्ती उत्पादों की एकाग्रता की गतिशीलता को दर्शाते हैं। मॉडल पैरामीटर $\ _मु$ उत्प्रेरक (तीसरा पदार्थ) की प्रारंभिक एकाग्रता समझ में आता है।

अधिक विस्तार से, विभिन्न मापदंडों के साथ गणना करके ब्रुसेलर के चरण चित्र का विकास देखा जा सकता है $\ _मु$ । इसकी वृद्धि के साथ, नोड पहले निर्देशांक के साथ धीरे-धीरे एक बिंदु पर शिफ्ट हो जाएगा (1, $\ _मु$ ) जब तक यह एक द्विभाजन मूल्य तक नहीं पहुंचता है $\ _मु$ = २। इस बिंदु पर, सीमा चक्र के जन्म में व्यक्त पोर्ट्रेट का गुणात्मक पुनर्गठन होता है। और वृद्धि के साथ $\ _मु$ इस चक्र के मापदंडों में केवल एक मात्रात्मक परिवर्तन होता है।

बिगाड़ने वाले के नीचे छिपा हुआ

 function brusselator(μ = 0.1, u0 = [0.1; 0.1]) function syst(du,u,p,t) du[1] = -(μ+1)*u[1] + u[1]*u[1]*u[2] + 1 du[2] = μ*u[1] - u[1]*u[1]*u[2] end tspan = (0.0, 10) # time period prob = ODEProblem(syst, u0, tspan) # problem to solve sol = solve(prob, RK4(),reltol=1e-6, timeseries_steps = 1) N = length(sol.u) J = length(sol.u[1]) U = zeros(N, J) for i in 1:N, j in 1:J U[i,j] = sol.u[i][j] #      end U end L = Array{Any}(undef, 10) function ploter(Answ) for i = 1:length(Answ) L[i] = layer(x = Answ[i][:,1], y = Answ[i][:,2], Geom.path ) end plot(L[1], L[2], L[3], L[4], L[5], L[6], L[7], L[8], L[9], L[10]) end SC = [ [0 0.5], [0 1.5], [2.5 0], [1.5 0], [0.5 1], [1 0], [1 1], [1.5 2], [0.1 0.1], [0.5 0.2] ] Ans1 = brusselator.( 0.1, SC ) Ans2 = brusselator.( 0.8, SC ) Ans3 = brusselator.( 1.6, SC ) Ans4 = brusselator.( 2.5, SC ) p1 = ploter(Ans1) p2 = ploter(Ans2) p3 = ploter(Ans3) p4 = ploter(Ans4) set_default_plot_size(16cm, 16cm) vstack( hstack(p1,p2), hstack(p3,p4) )

आज के लिए पर्याप्त है। अगली बार, हम यह जानने की कोशिश करेंगे कि नए कार्यों के लिए दूसरे ग्राफिक्स पैकेज का उपयोग कैसे करें, साथ ही साथ जूलिया के सिंटैक्स पर अपना हाथ टाइप करें। समस्याओं को हल करने की प्रक्रिया में, धीरे-धीरे पता लगाया जाना शुरू हो जाता है, न कि पेशेवरों और विपक्ष सीधे हैं ... बल्कि, सुविधाएं और असुविधाएं - इसके लिए एक अलग वार्तालाप समर्पित होना चाहिए। और, ज़ाहिर है, मैं अपने खेल की तुलना में अपने खेल की तुलना में अपने हेब्रा पर कुछ अधिक गंभीर देखना चाहूंगा - इसलिए, मैं जूलिस्ट से और अधिक गंभीर परियोजनाओं के बारे में बताने का आग्रह करता हूं, इससे कई और विशेष रूप से, इस अद्भुत भाषा को सीखने में मदद मिलेगी।

जूलिया और चरण गतिशील प्रणालियों के चित्र

थरथरानवाला

Brusselator

More articles: