👩🏼‍🔧 🚠 🖼️ जूलिया और आंशिक अंतर समीकरण 🤚🏾 ♌️ 🌳

सबसे विशिष्ट भौतिक मॉडल के उदाहरण पर, हम कार्यों के साथ काम करने के कौशल को मजबूत करेंगे और तेज, सुविधाजनक और सुंदर PyPlot विज़ुअलाइज़र से परिचित होंगे, जो कि मैटलपोटलिब पायथन की सारी शक्ति प्रदान करता है। बहुत सारे चित्र होंगे (स्पॉइलर के नीचे छिपे हुए)

हम यह सुनिश्चित करते हैं कि हुड के नीचे सब कुछ साफ और ताजा हो:

हुड के नीचे

]status Status `C:\Users\\.julia\environments\v1.0\Project.toml` [537997a7] AbstractPlotting v0.9.0 [ad839575] Blink v0.8.1 [159f3aea] Cairo v0.5.6 [5ae59095] Colors v0.9.5 [8f4d0f93] Conda v1.1.1 [0c46a032] DifferentialEquations v5.3.1 [a1bb12fb] Electron v0.3.0 [5789e2e9] FileIO v1.0.2 [5752ebe1] GMT v0.5.0 [28b8d3ca] GR v0.35.0 [c91e804a] Gadfly v1.0.0+ #master (https://github.com/GiovineItalia/Gadfly.jl.git) [4c0ca9eb] Gtk v0.16.4 [a1b4810d] Hexagons v0.2.0 [7073ff75] IJulia v1.13.0+ [`C:\Users\\.julia\dev\IJulia`] [6218d12a] ImageMagick v0.7.1 [c601a237] Interact v0.9.0 [b964fa9f] LaTeXStrings v1.0.3 [ee78f7c6] Makie v0.9.0+ #master (https://github.com/JuliaPlots/Makie.jl.git) [7269a6da] MeshIO v0.3.1 [47be7bcc] ORCA v0.2.0 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.0+ #master (https://github.com/sglyon/PlotlyJS.jl.git) [91a5bcdd] Plots v0.21.0 [438e738f] PyCall v1.18.5 [d330b81b] PyPlot v2.6.3 [c4c386cf] Rsvg v0.2.2 [60ddc479] StatPlots v0.8.1 [b8865327] UnicodePlots v0.3.1 [0f1e0344] WebIO v0.4.2 [c2297ded] ZMQ v1.0.0

अन्यथा, हमें आज के लिए वह सब कुछ मिलेगा जो हमें चाहिए

 julia>] pkg> add PyCall pkg> add LaTeXStrings pkg> add PyPlot pkg> build PyPlot #     build #    -      ,    pkg> add Conda #    Jupyter -    pkg> add IJulia #      pkg> build IJulia #     build

अब कार्यों के लिए!

समीकरण साधना

भौतिक विज्ञान में, शब्द स्थानांतरण को अपरिवर्तनीय प्रक्रियाओं के रूप में समझा जाता है, जिसके परिणामस्वरूप द्रव्यमान, गति, ऊर्जा, आवेश, या कुछ अन्य भौतिक मात्रा का एक स्थानिक आंदोलन (स्थानांतरण) भौतिक प्रणाली में होता है।
रैखिक एक आयामी परिवहन समीकरण (या संवहन समीकरण) - सबसे सरल आंशिक अंतर समीकरण - के रूप में लिखा जाता है

आ ं श ि क आ ं श ि क आ ं श ि क आ ं श ि क

$\ frac {\ आंशिक U (x, t)} {\ आंशिक t} + c \ frac {\ आंशिक U (x, t)} {\ आंशिक x} = \ Phi (U, x, t)$

परिवहन समीकरण के संख्यात्मक समाधान के लिए, आप स्पष्ट अंतर योजना का उपयोग कर सकते हैं:

\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ _i_ {i-1} + \ Phi_i} {२}

$\ frac {\ hat {U} _i-U_i} {\ tau} + c \ frac {U_i-U_ {i-1}} {\ Delta} = \ frac {\ _i_ {i-1} + \ Phi_i} {२}$

जहाँ $\ _ {यू}$ - ऊपरी समय परत पर ग्रिड फ़ंक्शन का मूल्य। यह सर्किट कर्टन संख्या के साथ स्थिर है। $K = c \ tau / \ Delta <1$

नॉनलाइनर ट्रांसफर

आ ं श ि क आ ं श ि क आ ं श ि क आ ं श ि क

$\ frac {\ आंशिक U (x, t)} {\ आंशिक t} + (C_0 + UC_1) \ frac {\ आंशिक U (x, t)} {\ आंशिक x} = \ Phi (U, x, T) )$

लाइन स्रोत (अवशोषण स्थानांतरण): $\ Phi (यू, एक्स, टी) = - बीयू$ । हम स्पष्ट अंतर योजना का उपयोग करते हैं:

$U ^ {j + 1} _i = \ left (1- \ frac {h_tB} {2} - \ frac {h_tC_0} {h_x} - \ frac {h_tC_1} {@_x} U ^ j_i \ right) U ^ j_i + U ^ j_ {i-1} \ left (\ frac {h_tC_0} {h_x} - \ frac {h_tB} {2} + \ frac {h_tC_1} {h_t} U ^ j_i \ right)$

 using Plots pyplot() a = 0.2 b = 0.01 ust = x -> x^2 * exp( -(xa)^2/b ) #   bord = t -> 0. #  #    - function transferequi(;C0 = 1., C1 = 0., B = 0., Nx = 50, Nt = 50, tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt b0 = 0.5B*dt c0 = C0*dt/dx c1 = C1*dt/dx print("Kurant: $c0 $c1") x = [i for i in range(0, length = Nx, step = dx)]#         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[:,1] = ust.(x) U[1,:] = bord.(t) for j = 1:Nt-1, i = 2:Nx U[i, j+1] = ( 1-b0-c0-c1*U[i,j] )*U[i,j] + ( c0-b0+c1*U[i,j] )*U[i-1,j] end t, x, U end t, X, Ans0 = transferequi( C0 = 4., C1 = 1., B = 1.5, tlmt = 0.2 ) plot(X, Ans0[:,1], lab = "t1") plot!(X, Ans0[:,10], lab = "t10") p = plot!(X, Ans0[:,40], lab = "t40") plot( p, heatmap(t, X, Ans0) ) #

परिणाम

अवशोषण को बढ़ाएं:

 t, X, Ans0 = transferequi( C0 = 2., C1 = 1., B = 3.5, tlmt = 0.2 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,10]) p = plot!(X, Ans0[:,40]) plot( p, heatmap(t, X, Ans0) )

परिणाम

 t, X, Ans0 = transferequi( C0 = 1., C1 = 15., B = 0.1, Nx = 100, Nt = 100, tlmt = 0.4 ) plot(X, Ans0[:,1]) plot!(X, Ans0[:,20]) plot!(X, Ans0[:,90])

लगभग खटखटाया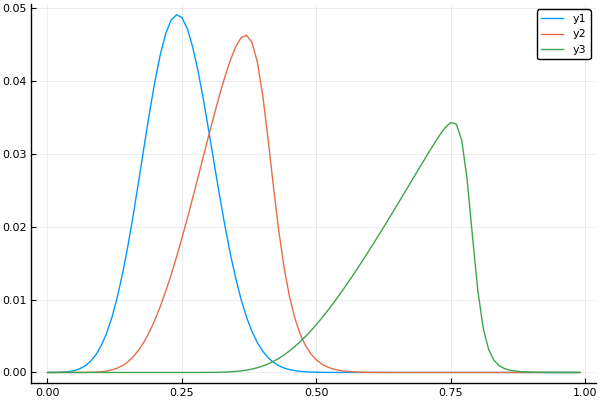

heatmap(t, X, Ans0)

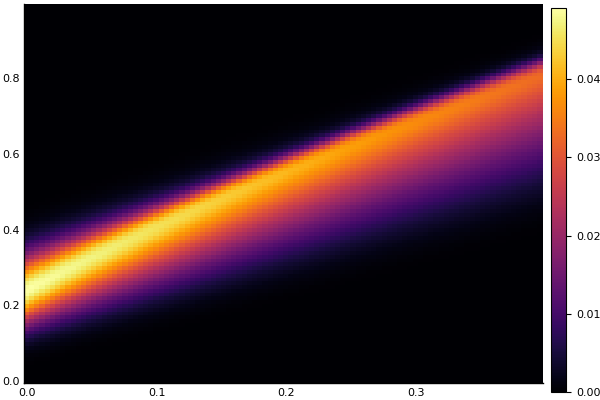
गर्मी का समीकरण

अंतर गर्मी समीकरण (या गर्मी प्रसार समीकरण) निम्नानुसार लिखा जाता है:

$\ frac {\ आंशिक T (x, t)} {\ आंशिक t} + D \ frac {\ आंशिक ^ 2 U (x, t)} {\ आंशिक x ^ 2} = \ phi (T, x, t) )$

यह एक पैराबोलिक समीकरण है जिसमें समय टी के संबंध में पहला व्युत्पन्न है और दूसरा स्थानिक समन्वय x के संबंध में है। यह तापमान की गतिशीलता का वर्णन करता है, उदाहरण के लिए, एक शीतलन या हीटिंग धातु की छड़ (फ़ंक्शन टी रॉड के साथ तालमेल के साथ तापमान प्रोफ़ाइल का वर्णन करता है)। गुणांक डी को तापीय चालकता (प्रसार) का गुणांक कहा जाता है। यह या तो स्थिर या निर्भर हो सकता है, दोनों स्पष्ट रूप से निर्देशांक पर, और वांछित फ़ंक्शन डी (टी, एक्स, टी) पर ही।

रैखिक समीकरण पर विचार करें (प्रसार गुणांक और गर्मी स्रोत तापमान स्वतंत्र हैं)। क्रमशः अंतर और स्पष्ट यूलर योजनाओं का उपयोग करते हुए एक अंतर समीकरण का अंतर:

$\ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T_ {i-1, n} -2T_ {i, n} + T_ {i 1 , n}} {\ Delta ^ 2} + \ phi_ {i, n} \\ \ frac {T_ {i, n + 1} -T_ {i, n}} {\ tau} = D \ frac {T {{ i-1, n + 1} -2T_ {i, n + 1} + T_ {i + 1, n + 1}} {\ Delta ^ 2} + \ phi_ {i, n}$

 δ(x) = x==0 ? 0.5 : x>0 ? 1 : 0 # -     startcond = x-> δ(x-0.45) - δ(x-0.55) #   bordrcond = x-> 0. #    D(u) = 1 #   Φ(u) = 0 #    #      LaTex    Tab # \delta press Tab -> δ function linexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)") x = [i for i in range(0, length = Nx, step = dx)] #         t = [i for i in range(0, length = Nt, step = dt)] #   -   U = zeros(Nx, Nt) U[: ,1] = startcond.(x) U[1 ,:] = U[Nt,:] = bordrcond.(t) for j = 1:Nt-1, i = 2:Nx-1 U[i, j+1] = U[i,j]*(1-2k*D( U[i,j] )) + k*U[i-1,j]*D( U[i-1,j] ) + k*U[i+1,j]*D( U[i+1,j] ) + dt*Φ(U[i,j]) end t, x, U end t, X, Ans2 = linexplicit( tlmt = 0.005 ) plot(X, Ans2[:,1], lab = "t1") plot!(X, Ans2[:,10], lab = "t10") p = plot!(X, Ans2[:,40], lab = "t40", title = "Explicit scheme") plot( p, heatmap(t, X, Ans2) )

परिणाम

हम निहित योजना और स्वीप विधि का उपयोग करते हैं

 function nonexplicit(Nx = 50, Nt = 40; tlmt = 0.01) dx = 1/Nx dt = tlmt/Nt k = dt/(dx*dx) print("Kurant: $k dx = $dx dt = $dt k<0.5? $(k<0.5)\n") x = [i for i in range(0, length = Nx, step = dx)] t = [i for i in range(0, length = Nt, step = dt)] U = zeros(Nx, Nt) η = zeros(Nx+1) ξ = zeros(Nx) U[: ,1] = startcond.(x) U[1 ,:] = bordrcond.(t) U[Nt,:] = bordrcond.(t) for j = 1:Nt-1 b = -1 - 2k*D( U[1,j] ) c = -k*D( U[2,j] ) d = U[1,j] + dt*Φ(U[1,j]) ξ[2] = c/b η[2] = -d/b for i = 2:Nx-1 a = -k*D( U[i-1,j] ) b = -2k*D( U[i,j] ) - 1 c = -k*D( U[i+1,j] ) d = U[i,j] + dt*Φ(U[i,j]) ξ[i+1] = c / (ba*ξ[i]) η[i+1] = (a*η[i]-d) / (ba*ξ[i]) end U[Nx,j+1] = η[Nx] for i = Nx:-1:2 U[i-1,j+1] = ξ[i]*U[i,j+1] + η[i] end end t, x, U end plot(X, Ans2[:,1], lab = "ex_t1") plot!(X, Ans2[:,10], lab = "ex_t10") plot!(X, Ans2[:,40], lab = "ex_t40") plot!(X, Ans3[:,1], lab = "non_t1") plot!(X, Ans3[:,10], lab = "non_t10") plot!(X, Ans3[:,40], lab = "non_t40", title = "Comparison schemes")

सर्किट तुलना

नॉनलाइनर हीट समीकरण

बहुत अधिक रोचक समाधान नॉनलाइन गर्मी समीकरण के लिए प्राप्त किया जा सकता है, उदाहरण के लिए, एक नॉनलाइन गर्मी स्रोत के साथ $\ phi (x, T) = 10 ^ 3 (T-T ^ 3)$ । यदि आप इसे इस रूप में सेट करते हैं, तो आपको थर्मल मोर्चों के रूप में एक समाधान मिलता है, जो प्राथमिक हीटिंग ज़ोन के दोनों किनारों पर फैलता है

 Φ(u) = 1e3*(uu^3) t, X, Ans4 = linexplicit( tlmt = 0.005 ) plot(X, Ans4[:,1], lab = "ex_t1") plot!(X, Ans4[:,10], lab = "ex_t10") plot!(X, Ans4[:,40], lab = "ex_t40", title = "Thermal front")

थर्मल सामने

इससे भी अधिक अप्रत्याशित समाधान प्रसार गुणांक की गैर-शुद्धता के साथ-साथ संभव है। उदाहरण के लिए, यदि आप लेते हैं $D (x, T) = T ^ 2$ , ए $\ phi (x, T) = 10 ^ 3T ^ {3.5}$ , तब व्यक्ति अपने प्राथमिक ताप (दहन के साथ एस मोड) के क्षेत्र में स्थानीय माध्यम के दहन के प्रभाव का निरीक्षण कर सकता है।
उसी समय, हम यह जांच करेंगे कि हमारी निहित योजना दोनों स्रोतों की गैर-मौजूदगी और प्रसार गुणांक के साथ कैसे काम करती है

 D(u) = u*u Φ(u) = 1e3*abs(u)^(3.5) t, X, Ans5 = linexplicit( tlmt = 0.0005 ) t, X, Ans6 = nonexplicit( tlmt = 0.0005 ) plot(X, Ans5[:,1], lab = "ex_t1") plot!(X, Ans5[:,10], lab = "ex_t10") p1 = plot!(X, Ans5[:,40], lab = "ex_t40", title = "Burning with aggravation") p2 = heatmap(abs.(Ans6-Ans5), title = "Difference") #      plot(p1, p2)

एस मोड

वेव समीकरण

हाइपरबोलिक वेव समीकरण

$\ frac {\ आंशिक ^ 2 U (x, t)} {\ आंशिक t ^ 2} = c ^ 2 \ frac {\ आंशिक ^ 2 U (x, t)} {\ आंशिक x ^ 2}$

फैलाव के बिना एक आयामी रैखिक तरंगों का वर्णन करता है। उदाहरण के लिए, एक तार में कंपन, तरल (गैस) में ध्वनि या निर्वात में विद्युत चुम्बकीय तरंगें (बाद वाले मामले में, समीकरण को वेक्टर रूप में लिखा जाना चाहिए)।

इस समीकरण को अनुमानित करने वाली सबसे सरल अंतर योजना एक स्पष्ट पांच-बिंदु योजना है

$\ frac {U ^ {n + 1} _i-2U ^ {n} _i + U ^ {n-1} _i} {\ tau ^ 2} = c ^ 2 \ frac {U ^ n_ {i +}} -2U ^ n_i + U ^ n_ {i-1}} {h ^ 2} \\ x_i = ih, \, t_n = \ tau$

"क्रॉस" नामक इस योजना में समय और स्थानिक समन्वय में सटीकता का दूसरा क्रम है और समय में तीन-परत है।

 #     ψ = x -> x^2 * exp( -(x-0.5)^2/0.01 ) #    ϕ(x) = 0 c = x -> 1 #     function pdesolver(N = 100, K = 100, L = 2pi, T = 10, a = 0.1 ) dx = L/N; dt = T/K; gam(x) = c(x)*c(x)*a*a*dt*dt/dx/dx; print("Kurant-Fridrihs-Levi: $(dt*a/dx) dx = $dx dt = $dt") u = zeros(N,K); x = [i for i in range(0, length = N, step = dx)] #      u[:,1] = ψ.(x); u[:,2] = u[:,1] + dt*ψ.(x); #     fill!( u[1,:], 0); fill!( u[N,:], ϕ(L) ); for t = 2:K-1, i = 2:N-1 u[i,t+1] = -u[i,t-1] + gam( x[i] )* (u[i-1,t] + u[i+1,t]) + (2-2*gam( x[i] ) )*u[i,t]; end x, u end N = 50; #     K = 40; #    a = 0.1; #    L = 1; #   T = 1; #   t = [i for i in range(0, length = K, stop = T)] X, U = pdesolver(N, K, L, T, a) #    plot(X, U[:,1]) plot!(X, U[:,40])

परिणाम

एक सतह का निर्माण करने के लिए, हम PyPlot को प्लॉट पर्यावरण के रूप में उपयोग करेंगे, लेकिन सीधे:

सतह ग्राफ

 using PyPlot surf(t, X, U)

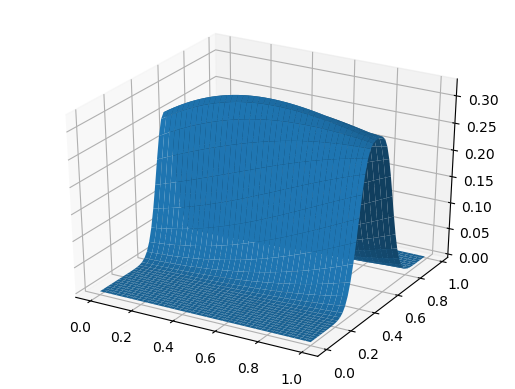
और मिठाई के लिए, तरंग समन्वय के आधार पर एक गति से फैलती है:

 ψ = x -> x>1/3 ? 0 : sin(3pi*x)^2 c = x -> x>0.5 ? 0.5 : 1 X, U = pdesolver(400, 400, 8, 1.5, 1) plot(X, U[:,1]) plot!(X, U[:,40]) plot!(X, U[:,90]) plot!(X, U[:,200], xaxis=("  ", (0, 1.5), 0:0.5:2) )

परिणाम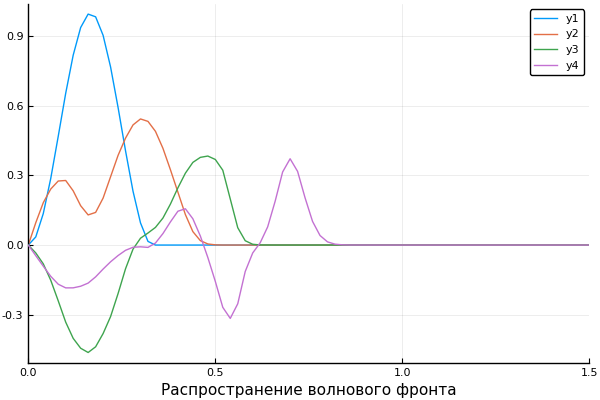

 U2 = [ U[i,j] for i = 1:60, j = 1:size(U,2) ] #    surf(U2) #

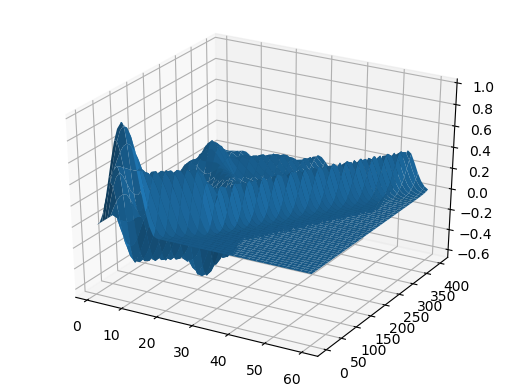
heatmap(U, yaxis=(" ", (0, 50), 0:10:50))

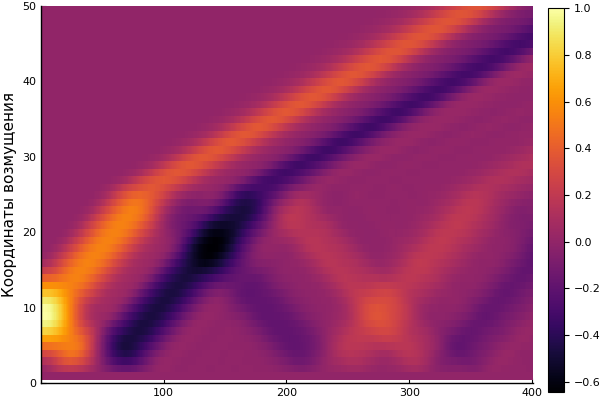
आज के लिए पर्याप्त है। अधिक विस्तृत समीक्षा के लिए:
पाइप्लॉट जीथुब से लिंक करता है , प्लॉट के अन्य उदाहरण पर्यावरण के रूप में इस्तेमाल किए जा रहे हैं, और जूलिया द्वारा एक अच्छी रूसी भाषा का ज्ञापन ।

जूलिया और आंशिक अंतर समीकरण

समीकरण साधना

नॉनलाइनर ट्रांसफर

गर्मी का समीकरण

नॉनलाइनर हीट समीकरण

वेव समीकरण

More articles: