एक वैरिएबल ऑटो-एनकोडर (ऑटो-एनकोडर) एक जेनरिक मॉडल है जो किसी दिए गए छिपे हुए स्थान में वस्तुओं को प्रदर्शित करना सीखता है।

कभी आपने सोचा है कि एक वैचारिक ऑटो-एनकोडर (VAE) मॉडल कैसे काम करता है? यह जानना चाहते हैं कि VAE उस डेटासेट की तरह नए उदाहरण कैसे उत्पन्न करता है जिस पर इसे प्रशिक्षित किया गया था? इस लेख को पढ़ने के बाद, आपको VAE की आंतरिक कार्यप्रणाली की एक सैद्धांतिक समझ मिलेगी, और आप इसे स्वयं भी लागू कर सकते हैं। फिर मैं हाथ से लिखे अंकों के एक सेट पर काम करने वाले VAE कोड को दिखाऊंगा, और नए अंक उत्पन्न करने में हमें कुछ मज़ा आएगा!

पीढ़ी के मॉडल

VAE एक जेनरेटिव मॉडल है - यह प्रशिक्षण डेटा की संभावना घनत्व (पीडीएफ) का अनुमान लगाता है। यदि इस तरह के मॉडल को प्राकृतिक छवियों में प्रशिक्षित किया जाता है, तो यह शेर की छवि को एक उच्च संभावना मूल्य और यादृच्छिक बकवास की छवि को कम मूल्य प्रदान करेगा।

VAE मॉडल प्रशिक्षित पीडीएफ से उदाहरण लेने में भी सक्षम है, जो सबसे ठंडा हिस्सा है, क्योंकि यह मूल डेटासेट के समान नए उदाहरण उत्पन्न कर सकता है!

मैं हस्तलिखित संख्या सेट MNIST का उपयोग करके VAE की व्याख्या करूँगा। मॉडल के लिए इनपुट डेटा प्रारूप में चित्र हैं

$\ mathbb {R} ^ {28 × 28}$ । मॉडल को इस बात की संभावना का आकलन करना चाहिए कि इनपुट एक अंक की तरह कितना दिखता है।

छवि मॉडलिंग कार्य

पिक्सल के बीच इंटरैक्शन एक मुश्किल काम है। यदि पिक्सेल एक दूसरे से स्वतंत्र हैं, तो आपको स्वतंत्र रूप से प्रत्येक पिक्सेल के पीडीएफ का अध्ययन करने की आवश्यकता है, जो कि आसान है। चयन भी सरल है - हम प्रत्येक पिक्सेल को अलग से लेते हैं।

लेकिन डिजिटल छवियों में, पिक्सल के बीच स्पष्ट निर्भरताएं हैं। यदि आप बाएं आधे पर चार की शुरुआत देखते हैं, तो आप बहुत आश्चर्यचकित होंगे यदि दाहिना आधा शून्य का पूरा होता है। पर क्यों? ।।

छिपी हुई जगह

आप जानते हैं कि प्रत्येक छवि में एक नंबर होता है। के लिए प्रवेश

$\ mathbb {R} ^ {28 × 28}$ स्पष्ट रूप से यह जानकारी नहीं है। लेकिन यह कहीं होना चाहिए ... यह "कहीं" एक छिपी हुई जगह है।

आप छिपी हुई जगह के बारे में सोच सकते हैं

$\ mathbb {R} ^ {k}$ जहां प्रत्येक वेक्टर शामिल है

$k$ एक छवि को प्रस्तुत करने के लिए आवश्यक जानकारी के टुकड़े। मान लीजिए कि पहले आयाम में एक संख्या एक अंक द्वारा दर्शाई गई है। दूसरा आयाम चौड़ाई हो सकता है। तीसरा कोण है, और इसी तरह।

हम एक व्यक्ति को दो चरणों में खींचने की प्रक्रिया की कल्पना कर सकते हैं। सबसे पहले, एक व्यक्ति निर्धारित करता है - होशपूर्वक या नहीं - संख्या की सभी विशेषताएं जो प्रदर्शित होने वाली हैं। इसके बाद, ये निर्णय कागज पर स्ट्रोक में बदल जाते हैं।

VAE इस प्रक्रिया को अनुकरण करने की कोशिश कर रहा है: एक दी गई छवि के लिए

$x$ हम कम से कम एक छिपे हुए वेक्टर को ढूंढना चाहते हैं जो इसका वर्णन कर सकते हैं; एक वेक्टर जिसमें उत्पादन के लिए निर्देश हैं

$x$ । कुल संभावना के सूत्र द्वारा इसे तैयार करना, हमें प्राप्त होता है

$P (x) = \ int P (x | z) P (z) dz$ ।

आइए इस समीकरण में कुछ उचित समझ रखें:

इंटीग्रल का मतलब है कि उम्मीदवारों को सभी छिपे हुए स्थान में तलाश किया जाना चाहिए।
प्रत्येक उम्मीदवार के लिए $z$ हम सवाल पूछते हैं: क्या यह उत्पन्न करना संभव है $x$ निर्देशों का उपयोग करना $z$ ? क्या यह काफी बड़ा है $P (x | z)$ ? उदाहरण के लिए, यदि $z$ अंक 7 के बारे में जानकारी एनकोड करता है, तो छवि 8 संभव नहीं है। हालांकि, छवि 1 स्वीकार्य है क्योंकि 1 और 7 समान हैं।
हमें एक अच्छा मिला। $z$ ? बहुत बढ़िया! लेकिन एक सेकंड रुकिए ... कितना है $z$ संभावना है? $P (z)$ काफी बड़ा है? उल्टे नंबर की छवि पर विचार करें 7. एक आदर्श मैच 7 का वर्णन करते हुए एक छिपा हुआ वेक्टर होगा, जहां कोण का आकार 180 ° पर सेट किया गया है। हालाँकि ऐसे $z$ इसकी संभावना कम है, क्योंकि आमतौर पर संख्या 180 ° के कोण पर नहीं लिखी जाती है।

VAE प्रशिक्षण का लक्ष्य अधिकतम करना है

$P (x)$ । हम मॉडल करेंगे

$P (x | z)$ बहुआयामी गाऊसी वितरण का उपयोग करना

$\ mathcal {N} (f (z), \ sigma ^ 2 \ cdot I)$ ।

$च (z)$ एक तंत्रिका नेटवर्क का उपयोग करके बनाया गया।

$\ _ सिग्मा$ पहचान मैट्रिक्स को गुणा करने के लिए एक हाइपरपैरेट है

$मैं$ ।

ध्यान रखें कि

$च$ - यह वह है जो हम एक प्रशिक्षित मॉडल का उपयोग करके नई छवियां उत्पन्न करने के लिए करेंगे। एक गौसियन वितरण को ओवरलैप करना केवल शैक्षिक उद्देश्यों के लिए है। यदि हम डिराक डेल्टा फ़ंक्शन (यानी, नियतात्मक) लेते हैं

$x = f (z)$ ), फिर हम ढाल वंश का उपयोग करके मॉडल को प्रशिक्षित करने में सक्षम नहीं होंगे!

छिपे हुए स्थान के चमत्कार

छिपे हुए स्थान के दृष्टिकोण में दो बड़ी समस्याएं हैं:

प्रत्येक आयाम में क्या जानकारी होती है? कुछ आयाम अमूर्त तत्वों से संबंधित हो सकते हैं, जैसे शैली। भले ही सभी आयामों की व्याख्या करना आसान था, हम डेटा सेट पर लेबल असाइन नहीं करना चाहते हैं। यह दृष्टिकोण अन्य डेटा सेट के पैमाने पर नहीं है।
आयामों के बीच संबंध होने पर छिपी हुई जगह को भ्रमित किया जा सकता है। उदाहरण के लिए, एक बहुत जल्दी तैयार की गई संख्या एक साथ कोणीय और पतले स्ट्रोक की उपस्थिति का कारण बन सकती है। इन निर्भरताओं को परिभाषित करना मुश्किल है।

गहरी शिक्षा बचाव के लिए आती है

यह पता चलता है कि प्रत्येक वितरण मानक बहुआयामी गाऊसी वितरण के बजाय एक जटिल फ़ंक्शन को लागू करके उत्पन्न किया जा सकता है।

हम चुनें

$P (z)$ एक मानक बहुआयामी गाऊसी वितरण के रूप में। इस प्रकार एक तंत्रिका नेटवर्क द्वारा मॉडलिंग की जाती है

$च$ दो चरणों में विभाजित किया जा सकता है:

पहली परतें गॉसियन डिस्ट्रीब्यूशन को छिपे हुए स्थान पर वास्तविक वितरण में मैप करती हैं। हम मापों की व्याख्या नहीं कर सकते, लेकिन इससे कोई फर्क नहीं पड़ता।
बाद की परतों को छिपी हुई जगह से प्रदर्शित किया जाएगा $P (x | z)$ ।

तो हम इस जानवर को कैसे प्रशिक्षित करते हैं?

के लिए सूत्र

$P (x)$ अघुलनशील, इसलिए, हम इसे मोंटे कार्लो विधि द्वारा अनुमानित करते हैं:

चयन $\ {z_i \} _ {i = 1} ^ n$ पिछले से $P (z)$
के साथ प्रतिदान $P (x) \ लगभग \ frac {1} {n} \ sum_ {i = 1} ^ n P (x | z_i)$

बहुत बढ़िया! तो बस बहुत सारे प्रयास करें

$z$ और बग प्रचार पार्टी शुरू करें!

दुर्भाग्य से

$x$ बहुत बहुआयामी, एक उचित अनुमान प्राप्त करने के लिए, कई नमूनों की आवश्यकता होती है। मेरा मतलब है अगर तुम कोशिश करो

$z$ , तो छवि पाने की संभावना क्या है जो कुछ इस तरह दिखती है

$x$ ? यह, वैसे, क्यों बताते हैं

$P (x | z)$ किसी भी संभावित छवि के लिए एक सकारात्मक संभावना मान निर्दिष्ट करना चाहिए, अन्यथा मॉडल सीखने में सक्षम नहीं होगा: नमूना

$z$ एक छवि में परिणाम होगा जो लगभग निश्चित रूप से अलग है

$x$ , और यदि संभावना 0 है, तो ग्रेडिएंट्स प्रचार नहीं कर पाएंगे।

इस समस्या को कैसे हल करें?

रास्ता काटो!

अधिकांश नमूने

$z$ चयन से कुछ भी नहीं जोड़ा जाएगा

$P (x)$ - वे इसकी सीमाओं से बहुत दूर हैं। अब, यदि आप पहले से जानते थे कि उन्हें कहां से लेना है ...

दर्ज कर सकते हैं

$Q (z | x)$ । यह

$क्यू$ को उच्च संभावना मान निर्दिष्ट करने के लिए प्रशिक्षित किया जाएगा

$z$ उत्पन्न होने की संभावना है

$x$ । अब आप मोंटे कार्लो विधि का उपयोग करके एक आकलन कर सकते हैं, जिससे बहुत कम नमूने ले सकते हैं

$क्यू$ ।

दुर्भाग्य से, एक नई समस्या पैदा होती है! इसके बजाय अधिकतम

$P (x) = \ int P (x | z) P (z) dz = \ mathbb {E} _ {z \ sim P (z)} P (x | z)$ हम अधिकतम

$\ mathbb {E} _ {z \ sim Q (z | x)} P (x | z)$ । वे एक दूसरे से कैसे संबंधित हैं?

विविधतापूर्ण निष्कर्ष

परिवर्तनीय निष्कर्ष एक अलग लेख का विषय है, इसलिए मैं इस पर यहां विस्तार से नहीं लिखूंगा। मैं केवल यह कह सकता हूं कि ये वितरण इस समीकरण से संबंधित हैं:

$log P (X) - \ mathcal {KL} [Q (z | x) || P (z | x)] = \ mathbb {E} _ {z \ sim Q (z | x)} [[P P (x | z)] - \ mathcal {KL} [Q (z | x) | पी (जेड)]$

$\ mathcal {KL}$ कुल्बैक - लाइबलर दूरी है , जो दो वितरणों की समानता का सहजता से आकलन करता है।

एक पल में, आप देखेंगे कि समीकरण के दाईं ओर अधिकतम कैसे करें। इस मामले में, बाईं ओर भी अधिकतम है:

$P (x)$ अधिकतम।
कितनी दूर है $Q (z | x)$ से $P (z | x)$ - अज्ञात एक वास्तविक - न्यूनतम किया जाएगा।

समीकरण के दाईं ओर का अर्थ यह है कि हमें यहां तनाव है:

एक ओर, हम अधिकतम कितना अच्छा करना चाहते हैं $x$ से डिकोड किया जाना चाहिए $z \ sim Q$ ।
दूसरी तरफ, हम चाहते हैं $Q (z | x)$ ( एनकोडर ) पहले की तरह ही था $P (z)$ (बहुआयामी गाऊसी वितरण)। इसे नियमितीकरण के रूप में देखा जा सकता है।

विचलन को कम से कम करना

$\ mathcal {KL}$ वितरण के सही चयन के साथ आसानी से प्रदर्शन किया। हम अनुकरण करेंगे

$Q (z | x)$ एक तंत्रिका नेटवर्क के रूप में, जिसका उत्पादन एक बहुआयामी गाऊसी वितरण के मापदंडों है:

औसत $\ mu_Q$
विकर्ण सहसंयोजक मैट्रिक्स $\ सिग्मा_ क्यू$

फिर विचलन

$\ mathcal {KL}$ विश्लेषणात्मक रूप से हल करने योग्य हो जाता है, जो हमारे लिए (और ग्रेडिएंट के लिए) बहुत अच्छा है।

डिकोडर भाग थोड़ा अधिक जटिल है। पहली नज़र में, मैं यह बताना चाहूंगा कि यह समस्या मोंटे कार्लो विधि द्वारा अस्वीकार्य है। लेकिन नमूना है

$z$ से

$क्यू$ ग्रेडिएंट के माध्यम से प्रचार करने की अनुमति नहीं देगा

$क्यू$ , क्योंकि चयन एक अलग संचालन नहीं है। यह एक समस्या है, तब से परतें जारी करने का वजन

$\ सिग्मा_ क्यू$ और

$\ mu_Q$ ।

नया पैरामीटर चाल

हम बदल सकते हैं

$क्यू$ एक गैर-यादृच्छिक यादृच्छिक चर का नियतात्मक पैराट्राइज्ड परिवर्तन:

मानक (मापदंडों के बिना) गाऊसी वितरण से एक नमूना।
वर्गमूल द्वारा नमूना गुणा $\ सिग्मा_ क्यू$ ।
परिणाम में जोड़ना $\ mu_Q$ ।

नतीजतन, हम एक समान वितरण प्राप्त करते हैं

$क्यू$ । अब भ्रूण ऑपरेशन मानक गाऊसी वितरण से आता है। नतीजतन, ग्रेडिएंट के माध्यम से प्रचार कर सकते हैं

$\ सिग्मा_ क्यू$ और

$\ mu_Q$ चूंकि अब ये निर्धारक मार्ग हैं।

परिणाम? मॉडल मापदंडों को समायोजित करने का तरीका जानने में सक्षम होगा

$क्यू$ : वह अच्छे के आसपास ध्यान केंद्रित करेगा

$z$ जो उत्पादन करने में सक्षम हैं

$x$ ।

यह सब एक साथ रखना

VAE मॉडल को समझना मुश्किल हो सकता है। हमने यहां बहुत सारी सामग्री की जांच की है जिसे पचाना मुश्किल है।

मुझे वीएई को लागू करने के लिए सभी चरणों को संक्षेप में प्रस्तुत करना चाहिए।

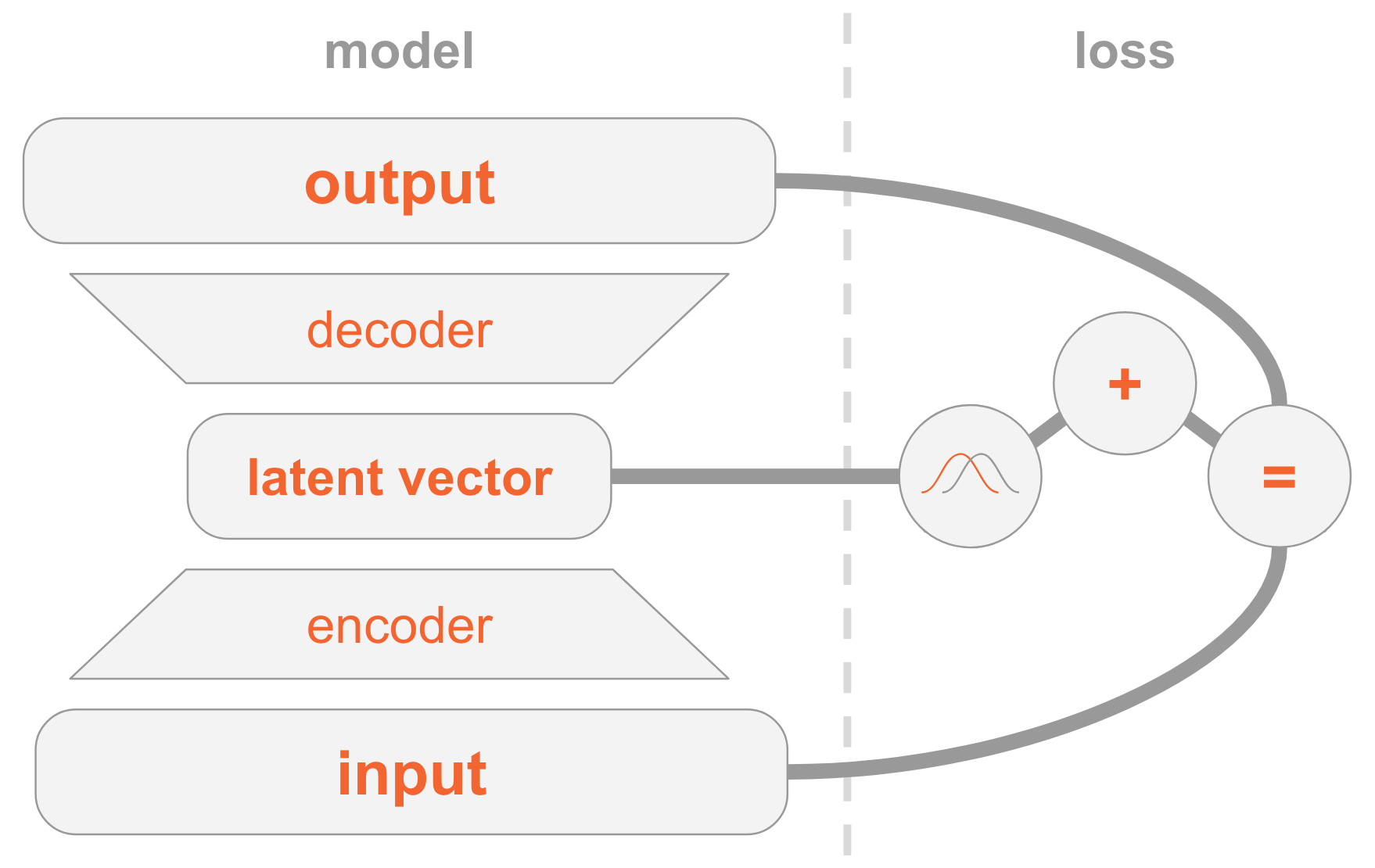
बाईं ओर हमारे पास एक मॉडल परिभाषा है:

इनपुट छवि एनकोडर नेटवर्क के माध्यम से प्रेषित होती है।
एनकोडर वितरण पैरामीटर प्रदान करता है $Q (z | x)$ ।
छिपे हुए वेक्टर $z$ से लिया गया $Q (z | x)$ । यदि एनकोडर अच्छी तरह से प्रशिक्षित है, तो ज्यादातर मामलों में $z$ एक विवरण शामिल हैं $x$ ।
डिकोडर डिकोड $z$ छवि में।

दाईं ओर, हमारे पास एक हानि कार्य है:

पुनर्प्राप्ति त्रुटि: आउटपुट इनपुट के समान होना चाहिए।
$Q (z | x)$ पिछले एक के समान होना चाहिए, अर्थात् एक बहुआयामी मानक सामान्य वितरण।

नई छवियां बनाने के लिए, आप सीधे पिछले वितरण से छिपे हुए वेक्टर का चयन कर सकते हैं और इसे एक छवि में डीकोड कर सकते हैं।

कार्य कोड

अब हम वीएई का अधिक विस्तार से अध्ययन करेंगे और कार्य कोड पर विचार करेंगे। आप वीएई को लागू करने के लिए आवश्यक सभी तकनीकी विवरणों को समझेंगे। एक बोनस के रूप में, मैं आपको एक दिलचस्प चाल दिखाऊंगा: छिपे हुए वेक्टर के कुछ आयामों के लिए विशेष भूमिकाएं कैसे असाइन करें ताकि मॉडल संकेतित संख्याओं के चित्र उत्पन्न करना शुरू कर दे।

import numpy as np import tensorflow as tf from tensorflow.examples.tutorials.mnist import input_data import matplotlib.pyplot as plt np.random.seed(42) tf.set_random_seed(42) %matplotlib inline

मैं आपको याद दिलाता हूं कि मॉडल MNIST पर प्रशिक्षित हैं - हस्तलिखित संख्याओं का एक सेट। इनपुट चित्र प्रारूप में आते हैं

$\ mathbb {R} ^ {28 × 28}$ ।

 mnist = input_data.read_data_sets('MNIST_data') input_size = 28 * 28 num_digits = 10

अगला, हम हाइपरपरमेटर्स को परिभाषित करते हैं।

मॉडल को प्रभावित करने के तरीके के बारे में जानने के लिए विभिन्न मूल्यों के साथ खेलने के लिए स्वतंत्र महसूस करें।

 params = { 'encoder_layers': [128], #       'decoder_layers': [128], #    (CNN ,     ) 'digit_classification_layers': [128], #   ,   'activation': tf.nn.sigmoid, #      'decoder_std': 0.5, #   P(x|z)   'z_dim': 10, #    'digit_classification_weight': 10.0, #   ,   'epochs': 20, 'batch_size': 100, 'learning_rate': 0.001 }

आदर्श

मॉडल में तीन सबनेट होते हैं:

हो जाता है $x$ (छवि), इसे एक वितरण में एनकोड करता है $Q (z | x)$ छिपी हुई जगह में।
हो जाता है $z$ छिपे हुए स्थान में (छवि का कोड प्रतिनिधित्व), इसे संबंधित छवि में डिकोड करता है $च (z)$ ।
हो जाता है $x$ और 10-आयामी परत के साथ तुलना करके संख्या निर्धारित करता है, जहां i-th मान में i-th संख्या की संभावना होती है।

पहले दो सबनेट शुद्ध VAE की नींव हैं।

तीसरा एक सहायक कार्य है जो छवि में पाई गई संख्याओं को एनकोड करने के लिए कुछ छिपे हुए आयामों का उपयोग करता है। मैं समझाता हूं कि क्यों: पहले हमने चर्चा की थी कि हमें परवाह नहीं है कि छिपे हुए स्थान के प्रत्येक आयाम में क्या जानकारी है। एक मॉडल किसी भी जानकारी को कोड करना सीख सकता है जिसे वह अपने कार्य के लिए मूल्यवान समझता है। चूंकि हम डेटा सेट से परिचित हैं, हम आयाम के महत्व को जानते हैं, जिसमें अंकों का प्रकार (यानी इसका संख्यात्मक मान) होता है। और अब हम उसे यह जानकारी प्रदान करके मॉडल की मदद करना चाहते हैं।

किसी दिए गए प्रकार के अंक के लिए, हम सीधे इसे सांकेतिक शब्दों में बदलना करते हैं, अर्थात्, हम आकार के एक वेक्टर का उपयोग करते हैं। 10. ये दस नंबर एक छिपे हुए वेक्टर से जुड़े हैं, इसलिए जब इस वेक्टर को एक छवि में डिकोड किया जाता है, तो मॉडल डिजिटल जानकारी का उपयोग करेगा।

प्रत्यक्ष कोडिंग वेक्टर मॉडल प्रदान करने के दो तरीके हैं:

इसे मॉडल के इनपुट के रूप में जोड़ें।
इसे एक लेबल के रूप में जोड़ें, ताकि मॉडल स्वयं पूर्वानुमान की गणना करेगा: हम एक और सबनेट जोड़ेंगे जो 10-आयामी वेक्टर की भविष्यवाणी करता है, जहां हानि फ़ंक्शन अपेक्षित आगे कोडिंग वेक्टर के साथ क्रॉस एन्ट्रॉपी है।

दूसरा विकल्प चुनें। क्यों? ठीक है, तो जब आप दो तरीकों से मॉडल का परीक्षण कर सकते हैं:

छवि को इनपुट के रूप में निर्दिष्ट करें और एक छिपे हुए वेक्टर को प्रदर्शित करें।
एक छिपे हुए वेक्टर को इनपुट के रूप में निर्दिष्ट करें और एक छवि उत्पन्न करें।

चूंकि हम पहले विकल्प का समर्थन करना चाहते हैं, इसलिए हम मॉडल को इनपुट के रूप में एक अंक नहीं दे सकते, क्योंकि हम परीक्षण के दौरान इसे जानना नहीं चाहते हैं। इसलिए, मॉडल को इसकी भविष्यवाणी करना सीखना चाहिए।

 def encoder(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) mu = tf.layers.dense(x, params['z_dim']) var = 1e-5 + tf.exp(tf.layers.dense(x, params['z_dim'])) return mu, var def decoder(z, layers): for layer in layers: z = tf.layers.dense(z, layer, activation=params['activation']) mu = tf.layers.dense(z, input_size) return tf.nn.sigmoid(mu) def digit_classifier(x, layers): for layer in layers: x = tf.layers.dense(x, layer, activation=params['activation']) logits = tf.layers.dense(x, num_digits) return logits

 images = tf.placeholder(tf.float32, [None, input_size]) digits = tf.placeholder(tf.int32, [None]) #        encoder_mu, encoder_var = encoder(images, params['encoder_layers']) #     ,  #     eps = tf.random_normal(shape=[tf.shape(images)[0], params['z_dim']], mean=0.0, stddev=1.0) z = encoder_mu + tf.sqrt(encoder_var) * eps # classify the digit digit_logits = digit_classifier(images, params['digit_classification_layers']) digit_prob = tf.nn.softmax(digit_logits) #     ,  #    decoded_images = decoder(tf.concat([z, digit_prob], axis=1), params['decoder_layers'])

 #    ,    #    loss_reconstruction = -tf.reduce_sum( tf.contrib.distributions.Normal( decoded_images, params['decoder_std'] ).log_prob(images), axis=1 ) #         . #      , #         #  ,  KL-   # ,    loss_prior = -0.5 * tf.reduce_sum( 1 + tf.log(encoder_var) - encoder_mu ** 2 - encoder_var, axis=1 ) loss_auto_encode = tf.reduce_mean( loss_reconstruction + loss_prior, axis=0 ) # digit_classification_weight      , #      loss_digit_classifier = params['digit_classification_weight'] * tf.reduce_mean( tf.nn.sparse_softmax_cross_entropy_with_logits(labels=digits, logits=digit_logits), axis=0 ) loss = loss_auto_encode + loss_digit_classifier train_op = tf.train.AdamOptimizer(params['learning_rate']).minimize(loss)

ट्रेनिंग

हम दो नुकसान कार्यों के अनुकूलन के लिए एक मॉडल को प्रशिक्षित करेंगे - VAE और वर्गीकरण - SGD का उपयोग करते हुए।

प्रत्येक युग के अंत में, हम छिपे हुए वैक्टरों का चयन करते हैं और उन्हें छवियों में डिकोड करते हैं कि वे यह देख सकें कि किस प्रकार मॉडल की पीढ़ी की शक्ति युगों में सुधार करती है। नमूना लेने की विधि इस प्रकार है:

स्पष्ट रूप से उन आयामों को सेट करें जिनका उपयोग उस अंक द्वारा वर्गीकृत करने के लिए किया जाता है जिसे हम उत्पन्न करना चाहते हैं। उदाहरण के लिए, यदि हम संख्या 2 की एक छवि बनाना चाहते हैं, तो हम माप निर्धारित करते हैं $[0010000000]$ ।
बहुआयामी सामान्य वितरण के अन्य आयामों से बेतरतीब ढंग से चयन करें। इस युग में उत्पन्न होने वाली विभिन्न संख्याओं के लिए ये मूल्य हैं। इसलिए हमें इस बात का अंदाजा हो जाता है कि अन्य आयामों में क्या कूटबद्ध है, उदाहरण के लिए, लिखावट शैली।

चरण 1 का अर्थ यह है कि अभिसरण के बाद, मॉडल को इन माप सेटिंग्स द्वारा इनपुट छवि में आंकड़े को वर्गीकृत करने में सक्षम होना चाहिए। हालाँकि, इनका उपयोग चित्र बनाने के लिए डिकोडिंग चरण में भी किया जाता है। यही है, डिकोडर सबनेट जानता है: जब माप 2 नंबर के अनुरूप होता है, तो उसे इस संख्या के साथ एक चित्र उत्पन्न करना चाहिए। इसलिए, यदि हम माप को मैन्युअल रूप से संख्या 2 पर सेट करते हैं, तो हमें इस आंकड़े की एक उत्पन्न छवि मिलेगी।

 samples = [] losses_auto_encode = [] losses_digit_classifier = [] with tf.Session() as sess: sess.run(tf.global_variables_initializer()) for epoch in xrange(params['epochs']): for _ in xrange(mnist.train.num_examples / params['batch_size']): batch_images, batch_digits = mnist.train.next_batch(params['batch_size']) sess.run(train_op, feed_dict={images: batch_images, digits: batch_digits}) train_loss_auto_encode, train_loss_digit_classifier = sess.run( [loss_auto_encode, loss_digit_classifier], {images: mnist.train.images, digits: mnist.train.labels}) losses_auto_encode.append(train_loss_auto_encode) losses_digit_classifier.append(train_loss_digit_classifier) sample_z = np.tile(np.random.randn(1, params['z_dim']), reps=[num_digits, 1]) gen_samples = sess.run(decoded_images, feed_dict={z: sample_z, digit_prob: np.eye(num_digits)}) samples.append(gen_samples)

आइए देखें कि दोनों नुकसान कार्य अच्छे लगते हैं, अर्थात् वे घटते हैं:

 plt.subplot(121) plt.plot(losses_auto_encode) plt.title('VAE loss') plt.subplot(122) plt.plot(losses_digit_classifier) plt.title('digit classifier loss') plt.tight_layout()

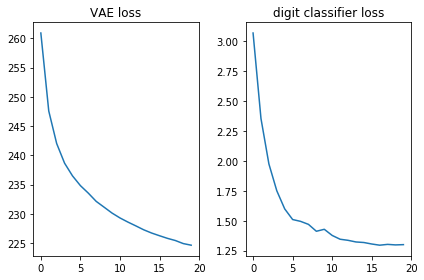
इसके अलावा, आइए उत्पन्न चित्रों को प्रदर्शित करें और देखें कि क्या मॉडल वास्तव में हस्तलिखित संख्याओं के साथ चित्र बना सकता है:

 def plot_samples(samples): IMAGE_WIDTH = 0.7 plt.figure(figsize=(IMAGE_WIDTH * num_digits, len(samples) * IMAGE_WIDTH)) for epoch, images in enumerate(samples): for digit, image in enumerate(images): plt.subplot(len(samples), num_digits, epoch * num_digits + digit + 1) plt.imshow(image.reshape((28, 28)), cmap='Greys_r') plt.gca().xaxis.set_visible(False) if digit == 0: plt.gca().yaxis.set_ticks([]) plt.ylabel('epoch {}'.format(epoch + 1), verticalalignment='center', horizontalalignment='right', rotation=0, fontsize=14) else: plt.gca().yaxis.set_visible(False) plot_samples(samples)

निष्कर्ष

यह देखना अच्छा है कि एक साधारण प्रत्यक्ष वितरण नेटवर्क (बिना फैंसी कनवल्शन के) केवल 20 युगों में सुंदर चित्र बनाता है। मॉडल ने संख्याओं के लिए विशेष माप का उपयोग करना जल्दी से सीखा: 9 वें युग में, हम पहले से ही उन संख्याओं के अनुक्रम को देखते हैं जिन्हें हम उत्पन्न करने की कोशिश कर रहे थे।

प्रत्येक युग में अन्य आयामों के लिए विभिन्न यादृच्छिक मूल्यों का उपयोग किया जाता है, इसलिए शैली युगों के बीच भिन्न होती है, लेकिन यह उनके भीतर समान है: कम से कम कुछ के भीतर। उदाहरण के लिए, 18 वें में, 20 की तुलना में सभी संख्याएं मोटी हैं।

नोट

लेख मेरे अनुभव और निम्नलिखित स्रोतों पर आधारित है:

विभिन्न ऑटो-एनकोडर्स: सिद्धांत और कार्य कोड