❗️ 🚺 🧜 परिप्रेक्ष्य: मल्टीकेलेट एस 1 🍈 👩🏼‍🌾 🤚

इसलिए, अगली पीढ़ी के बहुकोशिकीय प्रोसेसर के बारे में बात करने का समय आ गया है: MultiClet S1। यदि यह आपके बारे में पहली बार सुन रहा है, तो इन लेखों में वास्तुकला के इतिहास और विचारधारा की जांच करना सुनिश्चित करें:

फिलहाल, नया प्रोसेसर विकास के अधीन है, लेकिन पहले परिणाम सामने आ चुके हैं और आप इसका मूल्यांकन कर सकते हैं कि यह क्या करने में सक्षम होगा।

आइए सबसे बड़े परिवर्तनों के साथ शुरू करें: बुनियादी विशेषताएं।

खासियत है।

यह निम्नलिखित संकेतक प्राप्त करने की योजना है:

कोशिकाओं की संख्या: 64
तकनीकी प्रक्रिया: 28 एनएम
घड़ी की आवृत्ति: 1.6 गीगाहर्ट्ज़
चिप पर मेमोरी का आकार: 8 एमबी
क्रिस्टल क्षेत्र: 40 मिमी ²
बिजली की खपत: 6 डब्ल्यू

2019 में निर्मित नमूनों के परीक्षणों के परिणामों के आधार पर वास्तविक संख्या की घोषणा की जाएगी। चिप की विशेषताओं के अलावा, प्रोसेसर 16 जीबी तक डीडीआर 4 3200 मेगाहर्ट्ज मानक रैम, पीसीआई एक्सप्रेस बस और पीएलएल का समर्थन करेगा।

यह ध्यान दिया जाना चाहिए कि 28 एनएम विनिर्माण प्रक्रिया सबसे कम घरेलू सीमा है जिसे उपयोग के लिए विशेष अनुमति की आवश्यकता नहीं है, इसलिए यह वह था जिसे चुना गया था। कोशिकाओं की संख्या से, विभिन्न विकल्पों पर विचार किया गया था: 128 और 256, लेकिन क्रिस्टल के क्षेत्र में वृद्धि के साथ, अस्वीकार का प्रतिशत बढ़ जाता है। हम 64 कोशिकाओं पर बसे और, तदनुसार, एक अपेक्षाकृत छोटा क्षेत्र, जो प्लेट पर उपयुक्त क्रिस्टल की एक बड़ी उपज देगा। आईसीएस के ढांचे के भीतर आगे विकास संभव है (मामले में प्रणाली) , जहां एक मामले में कई 64-सेल क्रिस्टल को संयोजित करना संभव होगा।

यह कहा जाना चाहिए कि प्रोसेसर का उद्देश्य और उपयोग मौलिक रूप से बदल रहा है। S1 एक माइक्रोप्रोसेसर नहीं होगा जिसे एम्बेड करने के लिए डिज़ाइन किया गया है, जैसा कि P1 और R1 थे, लेकिन गणना का एक त्वरक। GPGPU की तरह, एक S1- आधारित बोर्ड को नियमित पीसी के PCI एक्सप्रेस मदरबोर्ड में डाला जा सकता है और इसका उपयोग डाटा प्रोसेसिंग के लिए किया जा सकता है।

आर्किटेक्चर

S1 में, "मल्टीसेल" अब न्यूनतम कम्प्यूटेशनल इकाई है: कमांड के एक निश्चित अनुक्रम को निष्पादित करने वाली 4 कोशिकाओं का एक सेट। सबसे पहले इसे समूहों में बहुस्तरों को संयोजित करने की योजना थी, जिन्हें कमांडों के संयुक्त निष्पादन के लिए एक क्लस्टर कहा जाता था: एक क्लस्टर में 4 बहुस्तरीय होते थे, कुल मिलाकर एक क्रिस्टल पर 4 अलग-अलग क्लस्टर होते थे। हालांकि, प्रत्येक कोशिका का क्लस्टर में अन्य सभी कोशिकाओं के साथ एक पूर्ण संबंध होता है, और बांडों के समूह में वृद्धि के साथ यह बहुत अधिक हो जाता है, जो माइक्रोक्रेकिट के टोपोलॉजिकल डिजाइन को बहुत जटिल करता है और इसकी विशेषताओं को कम करता है। इसलिए, उन्होंने क्लस्टर डिवीजन को छोड़ने का फैसला किया, क्योंकि जटिलता परिणामों को सही नहीं ठहराती है। इसके अलावा, अधिकतम प्रदर्शन के लिए, प्रत्येक मल्टीसेल पर समानांतर में कोड को चलाने के लिए सबसे अधिक फायदेमंद है। कुल मिलाकर, अब प्रोसेसर में 16 अलग-अलग मल्टीकास्ट हैं।

एक मल्टीसेल, हालांकि इसमें 4 सेल होते हैं, एक 4-सेल R1 से भिन्न होता है, जिसमें प्रत्येक सेल की अपनी मेमोरी, नमूना कमांड का अपना ब्लॉक, अपना ALU होता है। S1 को थोड़ा अलग तरीके से व्यवस्थित किया गया है। ALU में 2 भाग होते हैं: एक फ्लोटिंग पॉइंट अंकगणितीय ब्लॉक और एक पूर्णांक अंकगणितीय ब्लॉक। प्रत्येक सेल में एक अलग पूर्णांक ब्लॉक होता है, लेकिन एक मल्टीसेल में फ्लोटिंग पॉइंट के साथ केवल दो ब्लॉक होते हैं, और इसलिए दो जोड़े कोशिकाएं उन्हें आपस में विभाजित करती हैं। यह मुख्य रूप से क्रिस्टल के क्षेत्र को कम करने के लिए किया गया था: 64-बिट फ्लोटिंग-पॉइंट अंकगणित, पूर्णांक अंकगणित के विपरीत, बहुत अधिक स्थान लेता है। प्रत्येक कोशिका पर ऐसा ALU होना निरर्थक है: आदेश प्राप्त करना ALU लोडिंग प्रदान नहीं करता है और वे निष्क्रिय हैं। ALU ब्लॉकों की संख्या कम करने और आदेशों और डेटा को प्राप्त करने की गति को बनाए रखते हुए, जैसा कि अभ्यास ने दिखाया है, समस्याओं को हल करने के लिए कुल समय व्यावहारिक रूप से नहीं बदलता है या थोड़ा बदल जाता है, और ALU ब्लॉक पूरी तरह से लोड होते हैं। इसके अलावा, फ्लोटिंग-पॉइंट अंकगणित का उपयोग अक्सर पूर्णांक के रूप में नहीं किया जाता है।

प्रोसेसर R1 और S1 के ब्लॉक का एक योजनाबद्ध दृश्य नीचे चित्र में दिखाया गया है। यहां:

सीयू (कंट्रोल यूनिट) - इंस्ट्रक्शन लाने वाली यूनिट
ALU _FX - पूर्णांक अंकगणित की अंकगणितीय तर्क इकाई
ALU _FP - अस्थायी बिंदु अंकगणित की अंकगणितीय तर्क इकाई
डीएमएस (डेटा मेमोरी शेड्यूलर) - डेटा मेमोरी कंट्रोल यूनिट
डीएम - डेटा मेमोरी
पीएमएस (प्रोग्राम मेमोरी शेड्यूलर) - प्रोग्राम मेमोरी कंट्रोल यूनिट
पीएम - कार्यक्रम स्मृति

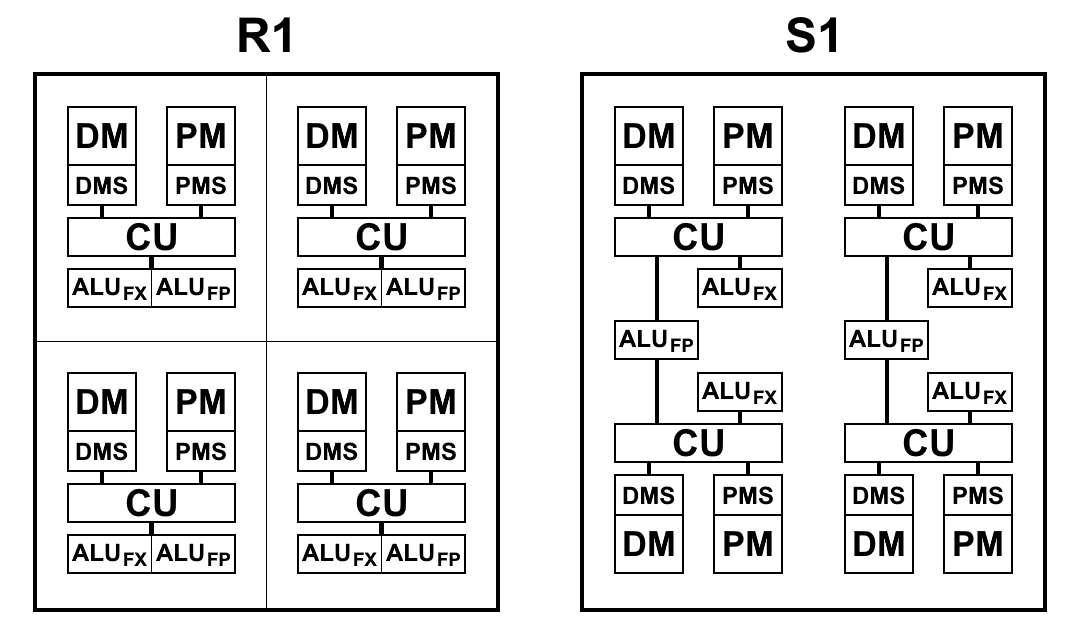
वास्तु अंतर S1:

टीमें अब पिछले पैराग्राफ से टीम परिणामों तक पहुंच सकती हैं। यह एक बहुत ही महत्वपूर्ण परिवर्तन है जो आपको कोड को ब्रांच करते समय संक्रमण को काफी तेज करने की अनुमति देता है। प्रोसेसर P1 और R1 के पास मेमोरी के वांछित परिणाम लिखने के अलावा और कोई विकल्प नहीं था और नए पैराग्राफ में बहुत पहले आदेशों के साथ तुरंत उन्हें वापस पढ़ें। चिप पर मेमोरी का उपयोग करते समय भी, लिखने और पढ़ने का संचालन 2 से 5 चक्रों से होता है, जिसे पिछले पैराग्राफ से कमांड के परिणाम का संदर्भ देकर बचाया जा सकता है।
मेमोरी और रजिस्टरों पर लिखना अब तुरंत होता है, न कि एक पैराग्राफ के अंत में, जो आपको पैराग्राफ के अंत से पहले कमांड लिखना शुरू करने की अनुमति देता है। नतीजतन, पैराग्राफ के बीच संभावित डाउनटाइम कम हो जाता है।
कमांड सिस्टम को अनुकूलित किया गया है, जिसका नाम है:
- जोड़ा गया 64-बिट पूर्णांक अंकगणित: इसके अलावा, घटाव, 32-बिट संख्याओं का गुणन, जो 64-बिट परिणाम देता है।
- मेमोरी से पढ़ने का तरीका बदल दिया गया है: अब किसी भी कमांड के लिए, आप केवल उस पते को निर्दिष्ट कर सकते हैं जिससे आप डेटा को एक तर्क के रूप में पढ़ना चाहते हैं, जबकि रीड एंड राइट कमांड के निष्पादन का क्रम संरक्षित है।
  
  इसने एक अलग मेमोरी रीड कमांड को भी अप्रचलित बना दिया। इसके बजाय, लोड मान कमांड का उपयोग लोड स्विच (पहले, प्राप्त करें ) में किया जाता है, जो एक तर्क के रूप में मेमोरी में पते को निर्दिष्ट करता है:
```
.data foo: .long 0x1234 .text habr: load_l foo ;      foo load_l [foo] ;    0x1234 add_l [foo], 0xABCD ;       ;   complete 
```
- एक कमांड प्रारूप जोड़ा गया है जो 2 निरंतर तर्कों के उपयोग की अनुमति देता है।
  पहले, आप केवल एक दूसरे तर्क के रूप में एक निरंतर निर्दिष्ट कर सकते थे, पहला तर्क हमेशा स्विच में परिणाम के लिए एक लिंक होना चाहिए। परिवर्तन सभी दो-तर्क टीमों पर लागू होता है। स्थिर क्षेत्र हमेशा 32 बिट होता है, इसलिए यह प्रारूप, उदाहरण के लिए, एक कमांड के साथ 64-बिट स्थिरांक उत्पन्न करने की अनुमति देता है।
  
  यह था:
```
 load_l 0x12345678 patch_q @1, 0xDEADBEEF 
```
  यह बन गया:
```
 patch_q 0x12345678, 0xDEADBEEF 
```
- संशोधित और पूरक वेक्टर डेटा प्रकार।
  जिसे "पैक्ड" डेटा प्रकार कहा जाता था, उसे अब वेक्टर कहा जा सकता है। पी 1 और आर 1 में, पैक्ड नंबरों पर संचालन केवल दूसरे तर्क के रूप में एक स्थिर था, अर्थात, जब जोड़ते समय, वेक्टर के प्रत्येक तत्व को एक ही नंबर के साथ जोड़ा गया था, और यह समझदारी से लागू नहीं किया जा सकता था। अब, इसी तरह के संचालन को दो पूर्ण वैक्टर पर लागू किया जा सकता है। इसके अलावा, वैक्टर के साथ काम करने का यह तरीका पूरी तरह से एलएलवीएम में वैक्टर के तंत्र के अनुरूप है, जो अब वेक्टर प्रकार का उपयोग करके कोड को उत्पन्न करने की अनुमति देता है।
```
 patch_q 0x00010002, 0x00030004 patch_q 0x00020003, 0x00040005 mul_ps @1, @2 ;  - 00020006000C0014 
```
प्रोसेसर के झंडे हटा दिए गए।

नतीजतन, झंडे के मूल्यों के आधार पर लगभग 40 टीमों को हटा दिया गया था। इसने टीमों की संख्या को काफी कम कर दिया है और, तदनुसार, क्रिस्टल का क्षेत्र। और सभी आवश्यक जानकारी अब स्विच सेल में सीधे संग्रहीत की जाती है।
- जब शून्य ध्वज के बजाय शून्य के साथ तुलना की जाती है, तो अब स्विच में केवल मूल्य का उपयोग किया जाता है
- साइन फ़्लैग के बजाय, कमांड के प्रकार से संबंधित थोड़ा सा अब उपयोग किया जाता है: बाइट के लिए 7 वें, शॉर्ट के लिए 15 वें, लंबे समय तक 31 वें, क्वाड के लिए 63 वें। इस तथ्य के कारण कि चरित्र 63 वें बिट तक गुणा करता है, प्रकार की परवाह किए बिना, आप विभिन्न प्रकारों की संख्या की तुलना कर सकते हैं:
```
 .data long: .long -0x1000 byte: .byte -0x10 .text habr: a := load_b [byte] ;     0xFFFFFFFFFFFFFFF0, ;   byte 7    63. b := loadu_b [byte] ;     0x00000000000000F0, ; ..  loadu_b    c := load_l [long] ;     0xFFFFFFFFFFFFF000. ge_l @a, @c ;   "  "  1: ;   31 ,   . lt_s @a, @b ; 1, .. b     complete 
```
- कैरी फ़्लैग की अब आवश्यकता नहीं है, क्योंकि 64-बिट अंकगणित है
पैराग्राफ से पैराग्राफ तक का संक्रमण समय 1 माप (R1 में 2-3 के बजाय) तक कम हो गया था

एलएलवीएम आधारित संकलक

S1 के लिए C भाषा संकलक R1 के समान है, और चूँकि वास्तुकला मूल रूप से नहीं बदली है, इसलिए पिछले लेख में वर्णित समस्याएं, दुर्भाग्य से, गायब नहीं हुई हैं।

हालाँकि, नए कमांड सिस्टम को लागू करने की प्रक्रिया में, कमांड कोड के अपडेट के कारण आउटपुट कोड की मात्रा अपने आप ही कम हो जाती है। इसके अलावा, कई और मामूली अनुकूलन हैं जो कोड में निर्देशों की संख्या को कम कर देंगे, जिनमें से कुछ पहले ही हो चुके हैं (उदाहरण के लिए, एक निर्देश के साथ 64-बिट स्थिरांक उत्पन्न करना)। लेकिन और भी अधिक गंभीर अनुकूलन हैं जिन्हें करने की आवश्यकता है, और उन्हें दक्षता और संयोजन दोनों के बढ़ते क्रम में बनाया जा सकता है:

दो स्थिरांक के साथ सभी दो-तर्क आदेश उत्पन्न करने की क्षमता।

पैच_क्यू के माध्यम से 64-बिट निरंतर बनाना केवल एक विशेष मामला है, लेकिन हमें एक सामान्य की आवश्यकता है। वास्तव में, इस अनुकूलन का उद्देश्य टीमों को पहले तर्क को एक स्थिर के रूप में बदलने की अनुमति देना है, क्योंकि दूसरा तर्क हमेशा एक स्थिर हो सकता है, और यह लंबे समय से लागू है। यह एक बहुत ही लगातार मामला नहीं है, लेकिन, उदाहरण के लिए, जब आपको किसी फ़ंक्शन को कॉल करने की आवश्यकता होती है और स्टैक के शीर्ष पर उससे वापसी का पता लिखना होता है, तो आप कर सकते हैं
```
 load_l func wr_l @1, #SP 
```
के लिए अनुकूलन
```
 wr_l func, #SP 
```
किसी भी कमांड में एक तर्क के माध्यम से मेमोरी एक्सेस का विकल्प।
उदाहरण के लिए, यदि आपको मेमोरी से दो नंबर जोड़ने की आवश्यकता है, तो आप कर सकते हैं
```
 load_l [foo] load_l [bar] add_l @1, @2 
```
के लिए अनुकूलन
```
 add_l [foo], [bar] 
```
यह अनुकूलन पिछले एक का एक विस्तार है, हालांकि, विश्लेषण पहले से ही यहां आवश्यक है: ऐसा प्रतिस्थापन केवल तभी किया जा सकता है यदि लोड किए गए मानों को केवल एक बार इस अतिरिक्त कमांड में उपयोग किया जाता है और कहीं नहीं। यदि रीडिंग परिणाम का उपयोग केवल दो कमांड में भी किया जाता है, तो मेमोरी से एक अलग कमांड के रूप में एक बार पढ़ना और अन्य दो में स्विच के माध्यम से इसे संदर्भित करना अधिक लाभदायक है।
आधार इकाइयों के बीच आभासी रजिस्टरों के हस्तांतरण का अनुकूलन।
R1 के लिए, सभी वर्चुअल रजिस्टरों का स्थानांतरण मेमोरी के माध्यम से किया गया था, जो बहुत बड़ी संख्या में रीड्स को मेमोरी में लिखता है, लेकिन पैराग्राफ के बीच डेटा ट्रांसफर करने का कोई अन्य तरीका नहीं था। S1 आपको पिछले पैराग्राफ के आदेशों के परिणामों तक पहुंचने की अनुमति देता है, इसलिए, सैद्धांतिक रूप से, कई मेमोरी ऑपरेशन को हटाया जा सकता है, जो सभी अनुकूलन के बीच सबसे बड़ा प्रभाव देगा। हालांकि, यह दृष्टिकोण अभी भी स्विच द्वारा सीमित है: 63 पिछले परिणामों से अधिक नहीं, अब तक वर्चुअल रजिस्टर के प्रत्येक हस्तांतरण से इस तरह लागू किया जा सकता है। यह कैसे करना एक तुच्छ कार्य नहीं है, और इसे हल करने के लिए संभावनाओं का विश्लेषण अभी तक किया जाना बाकी है। कंपाइलर स्रोत सार्वजनिक डोमेन में दिखाई दे सकते हैं, इसलिए यदि किसी के पास विचार हैं और आप विकास में शामिल होना चाहते हैं, तो आप यह कर सकते हैं।

मानक

चूंकि प्रोसेसर अभी तक चिप पर जारी नहीं किया गया है, इसलिए इसके वास्तविक प्रदर्शन का आकलन करना मुश्किल है। हालाँकि, RTL कर्नेल कोड पहले से ही तैयार है, जिसका अर्थ है कि आप सिमुलेशन या FPGA का उपयोग करके मूल्यांकन कर सकते हैं। निम्नलिखित मानदंड चलाने के लिए, हमने सटीक निष्पादन समय (उपायों में) की गणना करने के लिए ModelSim प्रोग्राम का उपयोग करके एक सिमुलेशन का उपयोग किया। चूंकि पूरे क्रिस्टल को अनुकरण करना मुश्किल है और इसमें बहुत लंबा समय लगता है, इसलिए, एक मल्टीसेल का अनुकरण किया गया था, और परिणाम 16 से गुणा किया गया था (यदि कार्य मल्टीथ्रेडिंग के लिए डिज़ाइन किया गया है), क्योंकि प्रत्येक मल्टीसेल दूसरों के स्वतंत्र रूप से काम कर सकता है।

उसी समय, वास्तविक हार्डवेयर पर प्रोसेसर कोड के प्रदर्शन का परीक्षण करने के लिए Xilinx Virtex-6 पर मल्टीसेल मॉडलिंग किया गया था।

CoreMark

CoreMark - माइक्रोकंट्रोलर और केंद्रीय प्रोसेसर के प्रदर्शन के व्यापक मूल्यांकन के लिए परीक्षणों का एक सेट, साथ ही साथ उनके सी-कंपाइलर भी। जैसा कि आप देख सकते हैं, एस 1 प्रोसेसर न तो एक है और न ही दूसरा है। हालांकि, यह पूरी तरह से मध्यस्थता कोड निष्पादित करने का इरादा है, अर्थात। कोई भी जो केंद्रीय प्रोसेसर पर चल सकता है। तो CoreMark S1 के प्रदर्शन का मूल्यांकन करने के लिए उपयुक्त है और खराब नहीं है।

CoreMark में लिंक्ड लिस्ट, मैट्रीस, एक स्टेट मशीन और CRC की गणना के साथ काम होता है। सामान्य तौर पर, अधिकांश कोड सख्ती से अनुक्रमिक हो जाते हैं (जो शक्ति के लिए बहुकोशिकीय हार्डवेयर समानता का परीक्षण करता है) और कई शाखाओं के साथ, यही वजह है कि संकलक क्षमताएं अंतिम प्रदर्शन में महत्वपूर्ण भूमिका निभाती हैं। संकलित कोड में काफी कम पैराग्राफ होते हैं और इस तथ्य के बावजूद कि उनके बीच संक्रमण की गति बढ़ गई है, शाखा में स्मृति के साथ काम करना शामिल है, जिसे हम अधिकतम से बचना चाहते हैं।

CoreMark स्कोरकार्ड:

	मल्टीलेट आर 1 (llvm संकलक)	मल्टीस्कलेट S1 (llvm संकलक)	एल्ब्रस -4 सी (आर 500 / ई)	टेक्सास इंस्टीट्यूट। AM5728 एआरएम कोर्टेक्स-ए 15	बाइकाल-T1	इंटेल कोर i7 7700K
निर्माण का वर्ष	2015	2019	2014	2018	2016	2017
घड़ी की आवृत्ति, मेगाहर्ट्ज	100	1600	700	1500	1200	4500
CoreMark समग्र स्कोर	59	18,356	1214	15,789	13142	182,128
कोरमार्क / मेगाहर्ट्ज	0.59	11.47	5.05	10.53	10.95	40.47

एक मल्टीसेल का परिणाम 1147, या 0.72 / मेगाहर्ट्ज है, जो कि आर 1 से अधिक है। यह नए प्रोसेसर में बहुकोशिकीय वास्तुकला के विकास के लाभों के बारे में बोलता है।

Whetstone

Whetstone - फ्लोटिंग पॉइंट नंबरों के साथ काम करते समय प्रोसेसर के प्रदर्शन को मापने के लिए परीक्षणों का एक सेट। यहां स्थिति बहुत बेहतर है: कोड अनुक्रमिक भी है, लेकिन बड़ी संख्या में शाखाओं के बिना और अच्छे आंतरिक संगति के साथ।

Whetstone में कई मॉड्यूल होते हैं, जो आपको न केवल समग्र परिणाम को मापने की अनुमति देता है, बल्कि प्रत्येक विशिष्ट मॉड्यूल पर प्रदर्शन भी करता है:

तत्वों को सरणी
पैरामीटर के रूप में सरणी
सशर्त कूदता है
पूर्णांक अंकगणित
त्रिकोणमितीय कार्य (तन, पाप, कोस)
प्रक्रिया कॉल
एरे संदर्भ
मानक कार्य (sqrt, ऍक्स्प, लॉग)

उन्हें श्रेणियों में विभाजित किया गया है: मॉड्यूल 1, 2, और 6 फ्लोटिंग पॉइंट ऑपरेशन के प्रदर्शन को मापते हैं (लाइनें MFLOPS1-3); मॉड्यूल 5 और 8 - गणितीय कार्य (COS MOPS, EXP MOPS); मॉड्यूल 4 और 7 - पूर्णांक अंकगणित (FIXPT MOPS, EQUAL MOPS); मॉड्यूल 3 - सशर्त कूदता है (IF MOPS)। नीचे दी गई तालिका में MWIPS की दूसरी पंक्ति एक सामान्य संकेतक है।

CoreMark के विपरीत, Whetstone की तुलना एक कोर पर या हमारे मामले में, एक मल्टीसेल पर की जाएगी। चूंकि विभिन्न प्रोसेसरों में कोर की संख्या बहुत भिन्न होती है, इसलिए, प्रयोग की शुद्धता के लिए, हम प्रति मेगाहर्ट्ज़ संकेतक पर विचार करते हैं।

वेटस्टोन स्कोरकार्ड:

प्रोसेसर	मल्टीकेलेट R1	MultiClet S1	कोर i7 4820K	एआरएम v8-A53
फ्रीक्वेंसी, मेगाहर्ट्ज	100	1600	3900	1300
MWIPS / मेगाहर्ट्ज	0.311	0.343	0.887	0.642
MFLOPS1 / मेगाहर्ट्ज	0.157	0.156	0.341	0.268
MFLOPS2 / MHz	0.153	0.111	0.308	0.241
MFLOPS3 / मेगाहर्ट्ज	0.029	0.124	0.167	0.239
COS MOPS / मेगाहर्ट्ज	0.018	0.008	0.023	0.028
EXP MOPS / मेगाहर्ट्ज	0.008	0.005	0.014	0.004
FIXPT MOPS / मेगाहर्ट्ज	0.714	0.116	0.998	1.197
यदि एमओपीएस / मेगाहर्ट्ज	0.081	0.196	1.504	1.436
एक्वल MOPS / मेगाहर्ट्ज	0.143	0.149	0.251	0439

Whetstone में CoreMark की तुलना में बहुत अधिक प्रत्यक्ष कम्प्यूटेशनल ऑपरेशन शामिल हैं (जो नीचे दिए गए कोड को देखते समय बहुत ध्यान देने योग्य हैं), इसलिए यहां याद रखना महत्वपूर्ण है: फ्लोटिंग-पॉइंट ALU की संख्या आधी है। हालांकि, गणना की गति R1 की तुलना में लगभग प्रभावित नहीं हुई थी।

कुछ मॉड्यूल एक बहुकोशिकीय वास्तुकला पर बहुत अच्छी तरह से फिट होते हैं। उदाहरण के लिए, मॉड्यूल 2 एक चक्र में बहुत सारे मानों को गिनता है, और प्रोसेसर और संकलक दोनों द्वारा दोहरे-सटीक फ्लोटिंग-पॉइंट संख्याओं के पूर्ण समर्थन के लिए धन्यवाद, संकलन के बाद हमें बड़े और सुंदर पैराग्राफ मिलते हैं जो वास्तव में एक बहुकोशिकीय वास्तुकला की कम्प्यूटेशनल क्षमताओं को प्रकट करते हैं:

120 टीमों के लिए बड़ा और सुंदर पैराग्राफ

 pa: SR4 := loadu_q [#SP + 16] SR5 := loadu_q [#SP + 8] SR6 := loadu_l [#SP + 4] SR7 := loadu_l [#SP] setjf_l @0, @SR7 SR8 := add_l @SR6, 0x8 SR9 := add_l @SR6, 0x10 SR10 := add_l @SR6, 0x18 SR11 := loadu_q [@SR6] SR12 := loadu_q [@SR8] SR13 := loadu_q [@SR9] SR14 := loadu_q [@SR10] SR15 := add_d @SR11, @SR12 SR11 := add_d @SR15, @SR13 SR15 := sub_d @SR11, @SR14 SR11 := mul_d @SR15, @SR5 SR15 := add_d @SR12, @SR11 SR12 := sub_d @SR15, @SR13 SR15 := add_d @SR14, @SR12 SR12 := mul_d @SR15, @SR5 SR15 := sub_d @SR11, @SR12 SR16 := sub_d @SR12, @SR11 SR17 := add_d @SR11, @SR12 SR11 := add_d @SR13, @SR15 SR13 := add_d @SR14, @SR11 SR11 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR11 SR15 := add_d @SR17, @SR11 SR16 := add_d @SR14, @SR13 SR13 := div_d @SR16, @SR4 SR14 := sub_d @SR15, @SR13 SR15 := mul_d @SR14, @SR5 SR14 := add_d @SR12, @SR15 SR12 := sub_d @SR14, @SR11 SR14 := add_d @SR13, @SR12 SR12 := mul_d @SR14, @SR5 SR14 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR11, @SR14 SR11 := add_d @SR13, @SR15 SR14 := mul_d @SR11, @SR5 SR11 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR13, @SR11 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR15 := mul_d @SR13, @SR5 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR15 SR14 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR11, @SR13 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR4 := loadu_q @SR4 SR5 := loadu_q @SR5 SR6 := loadu_q @SR6 SR7 := loadu_q @SR7 SR15 := mul_d @SR13, @SR5 SR8 := loadu_q @SR8 SR9 := loadu_q @SR9 SR10 := loadu_q @SR10 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR15 SR14 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR11, @SR13 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR15 := mul_d @SR13, @SR5 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR15, @SR12 SR15 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR15 SR14 := mul_d @SR13, @SR5 SR13 := add_d @SR16, @SR14 SR15 := add_d @SR17, @SR14 SR16 := add_d @SR11, @SR13 SR11 := div_d @SR16, @SR4 SR13 := sub_d @SR15, @SR11 SR15 := mul_d @SR13, @SR5 SR13 := add_d @SR12, @SR15 SR12 := sub_d @SR13, @SR14 SR13 := add_d @SR11, @SR12 SR12 := mul_d @SR13, @SR5 SR13 := sub_d @SR15, @SR12 SR16 := sub_d @SR12, @SR15 SR17 := add_d @SR14, @SR13 SR13 := add_d @SR11, @SR17 SR14 := mul_d @SR13, @SR5 SR5 := add_d @SR16, @SR14 SR13 := add_d @SR11, @SR5 SR5 := div_d @SR13, @SR4 wr_q @SR15, @SR6 wr_q @SR12, @SR8 wr_q @SR14, @SR9 wr_q @SR5, @SR10 complete

popcnt

वास्तुकला की विशेषताओं को स्वयं प्रतिबिंबित करने के लिए (संकलक की परवाह किए बिना), हम वास्तुशिल्प की सभी विशेषताओं को ध्यान में रखते हुए कोडांतरक में लिखे गए कुछ को मापेंगे। उदाहरण के लिए, एक 512-बिट संख्या (पॉपकंट) में यूनिट बिट्स की गिनती। स्पष्टता के लिए, हम एक मल्टीसेल के परिणाम लेंगे, ताकि उनकी तुलना R1 के साथ की जा सके।

तुलना तालिका, 32-बिट गणना चक्र प्रति घड़ी चक्रों की संख्या:

एल्गोरिथ्म	मल्टीस्कलेट r1	मल्टीस्कलेट एस 1 (एक मल्टीसेल)
BitHacks	5.0	2.625

नए अपडेट किए गए वेक्टर निर्देशों का उपयोग यहां किया गया था, जो हमें R1 कोडांतरक में लागू किए गए समान एल्गोरिथ्म की तुलना में निर्देशों की संख्या को आधा करने की अनुमति देता है। काम की गति, क्रमशः 2 गुना बढ़ गई।

popcnt

 bithacks: b0 := patch_q 0x1, 0x1 v0 := loadu_q [v] v1 := loadu_q [v+8] v2 := loadu_q [v+16] v3 := loadu_q [v+24] v4 := loadu_q [v+32] v5 := loadu_q [v+40] v6 := loadu_q [v+48] v7 := loadu_q [v+56] b1 := patch_q 0x55555555, 0x55555555 i00 := slr_pl @v0, @b0 i01 := slr_pl @v1, @b0 i02 := slr_pl @v2, @b0 i03 := slr_pl @v3, @b0 i04 := slr_pl @v4, @b0 i05 := slr_pl @v5, @b0 i06 := slr_pl @v6, @b0 i07 := slr_pl @v7, @b0 b2 := patch_q 0x33333333, 0x33333333 i10 := and_q @i00, @b1 i11 := and_q @i01, @b1 i12 := and_q @i02, @b1 i13 := and_q @i03, @b1 i14 := and_q @i04, @b1 i15 := and_q @i05, @b1 i16 := and_q @i06, @b1 i17 := and_q @i07, @b1 b3 := patch_q 0x2, 0x2 i20 := sub_pl @v0, @i10 i21 := sub_pl @v1, @i11 i22 := sub_pl @v2, @i12 i23 := sub_pl @v3, @i13 i24 := sub_pl @v4, @i14 i25 := sub_pl @v5, @i15 i26 := sub_pl @v6, @i16 i27 := sub_pl @v7, @i17 i30 := and_q @i20, @b2 i31 := and_q @i21, @b2 i32 := and_q @i22, @b2 i33 := and_q @i23, @b2 i34 := and_q @i24, @b2 i35 := and_q @i25, @b2 i36 := and_q @i26, @b2 i37 := and_q @i27, @b2 i40 := slr_pl @i20, @b3 i41 := slr_pl @i21, @b3 i42 := slr_pl @i22, @b3 i43 := slr_pl @i23, @b3 i44 := slr_pl @i24, @b3 i45 := slr_pl @i25, @b3 i46 := slr_pl @i26, @b3 i47 := slr_pl @i27, @b3 b4 := patch_q 0x4, 0x4 i50 := and_q @i40, @b2 i51 := and_q @i41, @b2 i52 := and_q @i42, @b2 i53 := and_q @i43, @b2 i54 := and_q @i44, @b2 i55 := and_q @i45, @b2 i56 := and_q @i46, @b2 i57 := and_q @i47, @b2 i60 := add_pl @i50, @i30 i61 := add_pl @i51, @i31 i62 := add_pl @i52, @i32 i63 := add_pl @i53, @i33 i64 := add_pl @i54, @i34 i65 := add_pl @i55, @i35 i66 := add_pl @i56, @i36 i67 := add_pl @i57, @i37 b5 := patch_q 0xf0f0f0f, 0xf0f0f0f i70 := slr_pl @i60, @b4 i71 := slr_pl @i61, @b4 i72 := slr_pl @i62, @b4 i73 := slr_pl @i63, @b4 i74 := slr_pl @i64, @b4 i75 := slr_pl @i65, @b4 i76 := slr_pl @i66, @b4 i77 := slr_pl @i67, @b4 b6 := patch_q 0x1010101, 0x1010101 i80 := add_pl @i70, @i60 i81 := add_pl @i71, @i61 i82 := add_pl @i72, @i62 i83 := add_pl @i73, @i63 i84 := add_pl @i74, @i64 i85 := add_pl @i75, @i65 i86 := add_pl @i76, @i66 i87 := add_pl @i77, @i67 b7 := patch_q 0x18, 0x18 i90 := and_q @i80, @b5 i91 := and_q @i81, @b5 i92 := and_q @i82, @b5 i93 := and_q @i83, @b5 i94 := and_q @i84, @b5 i95 := and_q @i85, @b5 i96 := and_q @i86, @b5 i97 := and_q @i87, @b5 iA0 := mul_pl @i90, @b6 iA1 := mul_pl @i91, @b6 iA2 := mul_pl @i92, @b6 iA3 := mul_pl @i93, @b6 iA4 := mul_pl @i94, @b6 iA5 := mul_pl @i95, @b6 iA6 := mul_pl @i96, @b6 iA7 := mul_pl @i97, @b6 iB0 := slr_pl @iA0, @b7 iB1 := slr_pl @iA1, @b7 iB2 := slr_pl @iA2, @b7 iB3 := slr_pl @iA3, @b7 iB4 := slr_pl @iA4, @b7 iB5 := slr_pl @iA5, @b7 iB6 := slr_pl @iA6, @b7 iB7 := slr_pl @iA7, @b7 wr_q @iB0, c wr_q @iB1, c+8 wr_q @iB2, c+16 wr_q @iB3, c+24 wr_q @iB4, c+32 wr_q @iB5, c+40 wr_q @iB6, c+48 wr_q @iB7, c+56 complete

Ethereum

बेंचमार्क बेशक, अच्छा है, लेकिन हमारे पास एक विशिष्ट कार्य है: एक संगणना त्वरक बनाने के लिए, और यह जानना अच्छा होगा कि यह वास्तविक दुनिया के कार्यों को कैसे संभालता है। आधुनिक क्रिप्टोकरेंसी इस तरह के सत्यापन के लिए सबसे उपयुक्त हैं, क्योंकि खनन एल्गोरिदम कई अलग-अलग उपकरणों पर चलते हैं और इसलिए तुलना के लिए एक बेंचमार्क के रूप में काम कर सकते हैं। हमने इथेरियम और एताश एल्गोरिथ्म के साथ शुरू किया, जो सीधे खनन डिवाइस पर चलता है।

एथेरियम का चुनाव निम्नलिखित विचारों के कारण था। जैसा कि आप जानते हैं, बिटकॉइन जैसे एल्गोरिदम विशेष रूप से विशेष एएसआईसी चिप्स द्वारा कुशलतापूर्वक कार्यान्वित किए जाते हैं, इसलिए बिटकॉइन खनन के लिए प्रोसेसर या वीडियो कार्ड का उपयोग और इसके क्लोन कम प्रदर्शन और उच्च बिजली की खपत के कारण आर्थिक रूप से नुकसानदेह हो जाते हैं। खनिकों का समुदाय, इस स्थिति से दूर होने के प्रयास में, अन्य एल्गोरिदम सिद्धांतों पर क्रिप्टोकरेंसी विकसित कर रहा है, खनन के लिए सामान्य प्रयोजन प्रोसेसर या वीडियो कार्ड का उपयोग करने वाले एल्गोरिदम के विकास पर ध्यान केंद्रित कर रहा है। यह प्रवृत्ति भविष्य में भी जारी रहने की संभावना है। एथेरियम इस दृष्टिकोण पर आधारित सबसे प्रसिद्ध क्रिप्टोक्यूरेंसी है। इथेरियम खनन के लिए मुख्य उपकरण वीडियो कार्ड हैं, जो दक्षता के मामले में (हैशेट / टीडीपी) सामान्य प्रयोजन प्रोसेसर से काफी आगे (कई बार) हैं।

एताश एक तथाकथित स्मृति बाध्य एल्गोरिथ्म है, अर्थात्। इसकी गणना का समय मुख्य रूप से स्मृति की मात्रा और गति से सीमित होता है, न कि स्वयं गणना की गति से। अब इथेरियम खनन के लिए, वीडियो कार्ड सबसे उपयुक्त हैं, लेकिन एक साथ कई ऑपरेशन करने की उनकी क्षमता बहुत मदद नहीं करती है, और वे अभी भी रैम की गति पर आराम करते हैं, जो इस लेख में स्पष्ट रूप से प्रदर्शित किया गया है। वहां से, आप यह बताने के लिए कि यह क्यों होता है, यह बताने के लिए एल्गोरिथ्म के संचालन को दर्शाती एक तस्वीर ले सकते हैं।

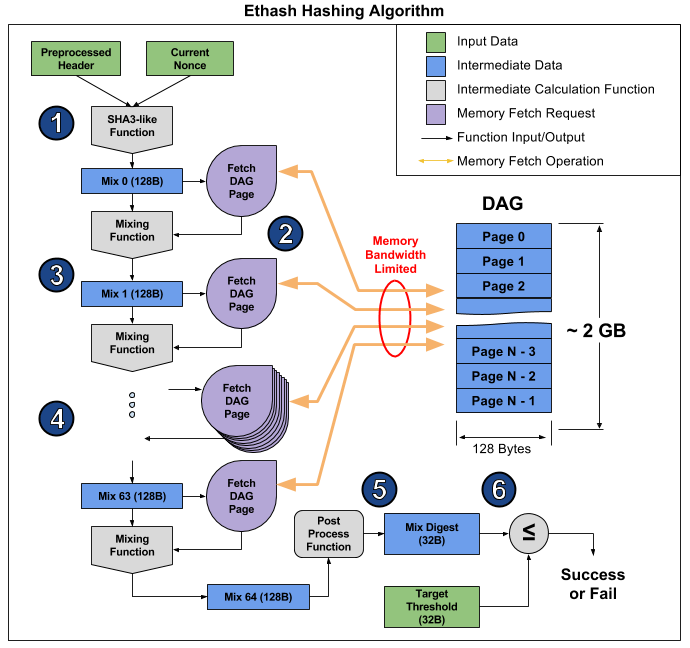
आलेख एल्गोरिथ्म को 6 बिंदुओं में तोड़ता है, लेकिन 3 चरणों को और भी स्पष्टता के लिए प्रतिष्ठित किया जा सकता है:

प्रारंभ: SHA-3 (512) मूल 128-बाइट मिक्स 0 (बिंदु 1) की गणना करने के लिए
अगले 128 बाइट्स को पढ़ने और मिक्सिंग फ़ंक्शन के माध्यम से पिछले वाले के साथ मिलाकर कुल 8 किलोबाइट (पैराग्राफ 2-4) पढ़कर मिक्स सरणी का 64-गुना पुनर्गणना करें।
अंतिम रूप और परिणाम का सत्यापन

RAM से यादृच्छिक 128 बाइट पढ़ने में जितना लगता है उससे कहीं अधिक समय लगता है। यदि आप MSI RX 470 ग्राफिक्स कार्ड लेते हैं, जिसमें 2048 कंप्यूटिंग डिवाइस और 211.2 GB / s की अधिकतम मेमोरी बैंडविड्थ है, तो प्रत्येक डिवाइस को लैस करने के लिए आपको 1 / (211.2 GB / (128 b * 2048)) - 1241 ns, या लगभग 1496 की आवश्यकता होती है दी गई आवृत्ति पर चक्र। मिक्सिंग फ़ंक्शन के आकार को देखते हुए, हम यह मान सकते हैं कि वीडियो कार्ड से मेमोरी पढ़ने में प्राप्त जानकारी को पुनर्गणना करने की तुलना में कई गुना अधिक समय लगता है। नतीजतन, एल्गोरिथ्म के चरण 2 में बहुत अधिक समय लगता है, चरण 1 और 3 की तुलना में, जो अंत में प्रदर्शन पर बहुत कम प्रभाव डालता है, इस तथ्य के बावजूद कि उनमें अधिक गणना होती है (मुख्य रूप से एसएचए -3 में)। आप बस इस वीडियो कार्ड के हैशटैर्ट पर देख सकते हैं: 26.375 मेगाचेस / एस सैद्धांतिक (केवल मेमोरी बैंडविड्थ द्वारा सीमित) बनाम 24 मेगाचेस / एस वास्तविक, अर्थात, चरण 1 और 3 केवल 10% समय लेते हैं।

S1 पर, सभी 16 मल्टीसेल समानांतर और अलग-अलग कोड पर काम कर सकते हैं। इसके अलावा, ड्यूल-चैनल रैम स्थापित किया जाएगा, साथ ही 8 मल्टीकास्ट के लिए एक चैनल। एताश एल्गोरिथ्म के चरण 2 में, हमारी योजना इस प्रकार है: एक मल्टीसेल मेमोरी से 128 बाइट्स पढ़ता है और उन्हें फिर से लिखना शुरू करता है, फिर अगला मेमोरी को पढ़ता है और रिकॉल करता है, और इसी तरह 8 वीं तक, यानी। स्मृति के 128 बाइट्स पढ़ने के बाद एक मल्टीसेल, सरणी को पुनर्गणना करने के लिए 7 * [128 बाइट्स का समय पढ़ें] है। यह माना जाता है कि इस तरह के पढ़ने में 16 चक्र होंगे, अर्थात्। रीकाउंटिंग के लिए 112 उपाय दिए गए हैं। मिक्सिंग फंक्शन की गणना करना एक ही क्लॉक साइकिल के बारे में है, इसलिए S1 प्रोसेसर के प्रदर्शन के लिए मेमोरी बैंडविड्थ के आदर्श अनुपात के करीब है। चूंकि समय दूसरे चरण में बर्बाद नहीं होता है, एल्गोरिथ्म के शेष हिस्सों को जितना संभव हो उतना अनुकूलित किया जाना चाहिए, क्योंकि तब वे वास्तव में प्रदर्शन को प्रभावित करते हैं।

SHA-3 (Keccak) C, . , SHA-3 (Keccak) 1550 . , 1550 + 64 * (16 + 112) = 9742 . 1.6 16 2.6 MHash/s.

	MultiClet S1	NVIDIA GeForce GTX 980 Ti	Radeon RX 470	Radeon RX Vega 64	NVIDIA GeForce GTX 1060	NVIDIA GeForce GTX 1080 Ti
कीमत		$650	$180	$500	$300	$700
	2.6 MHash/s	21.6 MHash/s	25.8 MHash/s	43.5 MHash/s	25 MHash/s	55 MHash/s
तेदेपा	6 W	250 W	120 W	295 W	120 W	250 W
/ TDP	0.43	0.09	0.22	0.15	0.22	0.21
	28	28	14	14	16	16

MultiClet S1 , 20 . , , S1 , 16 14 .

, . , .

, , . SDK, , , , .

परिप्रेक्ष्य: मल्टीकेलेट एस 1