अरे, पूरे ढेर, चलो कौशल को प्रशिक्षित करते हैं। मेरा सुझाव है कि गाइरस को सानना, यह मुझे लगता है, यह एक अलग, असामान्य प्रतिमान का उपयोग करना दिलचस्प है। अधिकांश डेवलपर्स के पास एल्गोरिदमाइजेशन का एक विकसित कौशल है - कार्य ईंटों में बदल जाता है, जिन्हें कनेक्ट करने की आवश्यकता होती है, चाल के अनुक्रम पर सोचने के लिए जो वांछित निष्कर्ष की ओर जाता है।

यहां, एक हफ्ते पहले, प्रोलॉग का उल्लेख किया गया था, मैं जवाब देना चाहता हूं कि प्रोलॉग भाषा समस्याओं को हल करने के लिए उपयुक्त है। मैंने पहले से ही इस विषय पर छुआ, और एल्गोरिदम के कार्यों के साथ एक साइट से मुझे उपलब्ध यादृच्छिक कार्यों के कई समाधानों का हवाला दिया, मैं यह बताना चाहूंगा कि कोई भी जटिल समाधान एक घोषणात्मक भाषा में उपलब्ध है, और यह धीमी गति से काम कर सकता है (अच्छी तरह से, शायद कभी नहीं। बहुत धीमी गति से नहीं)।

अगली समस्या पेश करने के लिए नीचे उतरने में लंबा समय लगा, और पहला समाधान पहले ही मिल चुका है, मैं समस्या का प्रदर्शन करता हूं और पता लगाता हूं कि यह कितना धीमा है।

प्रस्तावना इस मायने में दिलचस्प है कि आप एक कटौतीत्मक कार्यक्रम बना सकते हैं जो बहुत सारे समाधान दिखाता है और इसे सीमित भी कर सकता है, लेकिन पुनरावृति का रास्ता प्रदान नहीं करता है,
एल्गोरिथ्म विकसित किया जाएगा ~~solver~~ दुभाषिया।

तो, कार्य यह है :

बारिश के पानी को फँसाना ii
2 डी ऊंचाई के नक्शे में प्रत्येक इकाई सेल की ऊंचाई का प्रतिनिधित्व करने वाले सकारात्मक पूर्णांक के एक एमएक्सएन मैट्रिक्स को देखते हुए, पानी की मात्रा की गणना करें जो बारिश के बाद फंसने में सक्षम है।
ध्यान दें:
एम और एन दोनों 110 से कम हैं। प्रत्येक यूनिट सेल की ऊंचाई 0 से अधिक है और 20,000 से कम है।
उदाहरण:

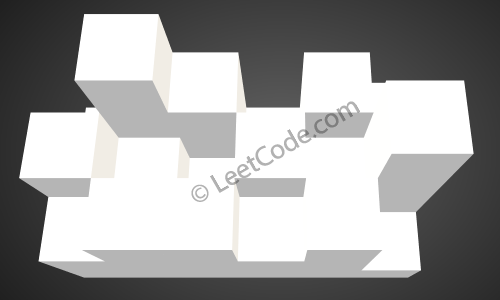
निम्नलिखित 3x6 ऊंचाई के नक्शे को देखते हुए:
[
[1,4,3,1,3,2]
[3,2,1,3,2,4]
[2,3,3,2,3,1]
]
वापसी ४।

एक समाधान तैयार करने के लंबे प्रयासों के बाद, मैं इस शब्द पर आया:
प्रत्येक सेल में अधिकतम पानी डालना आवश्यक है, जो इसके बाहर नहीं फैलता है । मैं प्रत्येक कोशिका में एक निश्चित मात्रा में पानी डालने का सुझाव देता हूं, लेकिन यह संभव है कि यह अधिकतम संभव मूल्य से कम हो।

यह इस तरह निकला:

reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!.

यह विधेय इनपुट सूची (मैट्रिक्स) को लेता है, और इसे एक मैट्रिक्स में एक समाधान में बदल देता है, जिसमें अन्य मान हैं जो एक मान्य उत्तर होगा। फिर एक और विधेय इन दो सूचियों को तत्व से लेता है और कुल राशि पाता है।

 repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X).

यह विधेय एक समाधान लेगा, और जांच करेगा कि क्या यह "सामान्य रूप से" भरा हुआ है, यदि यह समस्या की स्थिति को संतुष्ट करता है, तो यह समाधान है।

यह "उत्पन्न और सत्यापित" विधि है, हम कहते हैं कि मूल्य इस तरह के सेट में है और हम इस सेट के सभी तत्वों को संशोधित करते हैं, किसी प्रकार की निकास स्थिति की जांच करते हैं।

तो, फिर मैं पुट (वाल्स, एक्स 0, एक्स 1) के साथ एक नया समाधान प्राप्त करूंगा, यहां पहले स्थान पर, सभी संभावित ऊंचाइयों की सूची है जो इस मैट्रिक्स में हैं, जिसमें से हम प्रत्येक सेल के लिए संभव ऊंचाइयों का चयन करेंगे। इनपुट परीक्षणों के विश्लेषण के अनुसार, यह पता चला कि इस समस्या में पूरे सेल को भरना संभव है, अगर इसके चारों ओर इतना पानी डाला जा सकता है कि इसे "सिर के ऊपर" डाला जाए।

कुल मिलाकर, यह विधेय अधिक जटिल दिखता है, आपको उन लाइनों के त्रिभुज को संसाधित करना होगा जो एक 3x3 वर्ग बनाते हैं (हाँ, प्रोलॉग में कोई सरणी नहीं है, लेकिन यह इनपुट डेटा के विवरण की तरह दिखता है, हम इसे घोषणात्मक प्रोग्रामिंग में उपयोग करते हैं, आप सरणी में तत्वों के सूचकांकों के बारे में नहीं जानते हैं। , इसके सिर और पूंछ के साथ केवल एक सूची है, इसलिए बस एक टेम्पलेट का वर्णन करें जो इनपुट विनिर्देश से मेल खाता है)।

 puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St).

यह मैट्रिक्स के बाईपास को व्यक्त करने का तरीका है, जिसमें से आप पहली तीन (और आगे) पंक्तियों को ले सकते हैं, जिसमें से, आप बाएं से दाएं, तत्वों के त्रिभुज का भी चयन कर सकते हैं, और आठ पड़ोसियों के बीच परिदृश्य का एक [इताया] [यूटा] सेल होगा। Sel_biger (R2, V, R21) की मदद से इस सेल का एक नया अर्थ बनता है।

यह मान वर्तमान सेल पर सेट किया जा सकता है, यह संभव ऊंचाइयों में से एक हो सकता है, और यहां तक कि सूची को अवरोही क्रम में क्रमबद्ध किया गया है, ताकि पहले उच्चतम ऊंचाई हो जो सभी में उपलब्ध हो, और फिर किसी भी इसका पालन करें:

 sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X).

यह एक "निर्णय जनरेटर," का वर्णन था और फिर आपको यह सुनिश्चित करने की आवश्यकता है कि प्रत्येक बिंदु पर मनमाने ढंग से भरे ऊंचाइयों से प्राप्त मैट्रिक्स, उस उत्तर के समान है जिसकी हमें आवश्यकता है।

और इस तरह की स्थिति को खोजने के लिए आवश्यक था कि पानी छेदों में बसता है, मैं इसे इस तरह से डालने की कोशिश करूंगा:
एक वर्ग के नौ मान तीन से तीन होते हैं, केंद्र में हमेशा इतनी ऊंचाई होनी चाहिए कि यह इनपुट मैप का खंडन न करे, जिससे कि इन कोशिकाओं में मूल रूप से संतुलन परिवर्तन प्राप्त नहीं हुआ था, यदि ऊंचाई थी, तो इसके ऊपर भी कोशिकाएं नहीं होनी चाहिए, भले ही सब कुछ पानी से भर जाएगा, फिर यहां हम कह सकते हैं कि उच्च सेल को अपने आप से बने रहना चाहिए या उच्च मूल्य के साथ प्रतिस्थापित किया जाना चाहिए, लेकिन ऐसा है कि यह सभी पड़ोसियों के लिए समान है, अर्थात। कोशिकाओं को बाईं ओर, दाईं ओर और ऊपर से नीचे की ओर धारा से अधिक होना चाहिए या बराबर होना चाहिए, यदि सेल में अधिक पानी है, तो केवल अगर यह चारों ओर बढ़ गया है ...

 %%   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %%     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %%    , %        equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T).

और अंतिम दो विधेय, जो इनपुट मैट्रिक्स लेते हैं, एक उपयुक्त परिणाम की खोज शुरू करते हैं, अपने बीच के तत्वों के योग को घटाते हैं, और समस्या में आवश्यक अंतिम राशि पाते हैं:

 diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. %%  ,      sums(X,S):-reptest(X,X1),diffall(X,X1,S).

मैं उन परीक्षणों का प्रदर्शन करूंगा जो साइट ने प्रदान किए हैं।

 reptest(X0,X2):- flatten(X0,FX0), sort(0,>,FX0,Vals), repdown(X0,Vals,X0,X2),!. repdown(X0,Vals,X,X1):- puts(Vals,X0,X1), X\=X1, balns(X0,X1),!. repdown(_,_,X,X). puts(_,[],[]). puts(_,[X],[X]). puts(_,[X,Z],[X,Z]). puts(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!,sel_biger(R2,V,R21),puts(V,[R21,R3|T],St). puts(V,[R1,R2,R3|T],[R1|St]) :- puts(V,R2,R21),puts(V,[R21,R3|T],St). sel_biger(C,[H|_],H):-H>=C. sel_biger(C,[_|T],X):-sel_biger(C,T,X). %   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %    , %        equ(_,[],_,[]):-!. equ(C,_,C,_):-!. equ(C0,_,C,N):-C>C0,!,findall(X,(member(X,N),X<C),[]). equ(C0,[C0|T0],C,[C|T]):-!,equ(C0,T0,C,T). diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-reptest(X,X1),diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([],0),true). :-assert_are_equal(sums([[1]],0),true). :-assert_are_equal(sums([[2,3]],0),true). :-assert_are_equal(sums([[3],[2]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). %:-assert_are_equal(sums([[9,9,9,9,9,9,8,9,9,9,9],[9,0,0,0,0,0,1,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,0,0,0,0,0,0,0,0,0,9],[9,9,9,9,9,9,9,9,9,9,9]],215),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). %:-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true).

मुझे परीक्षणों पर टिप्पणी करनी थी। सब नहीं गुजरा।

कार्य यह है कि इसे कैसे गति दी जाए?

कुछ समाधान नहीं मिल सकते हैं, समाधानों की लंबी खोज के कारण, वे इस क्रम में बहुत धीरे-धीरे उत्पन्न होते हैं, यहां जटिलता शायद n है!, सरणी के प्रत्येक सेल के लिए सभी संभावित मानों को क्रमबद्ध किया गया है।

एक प्रोग्रामिंग सिस्टम में प्रतिबंधों में इस कार्य को व्यक्त करना सुविधाजनक है, सिर्फ प्रोलॉग पर इसे इस तरह कहा जाता है: सीएलपी (एफडी): परिमित तर्क प्रोग्रामिंग परिमित डोमेन पर।

clp (fd) मानक SWI-Prolog वितरण में शामिल एक पुस्तकालय है। यह उन समस्याओं को हल करता है जिसमें चर के सेट शामिल होते हैं, जहां चर के बीच संबंधों को संतुष्ट करने की आवश्यकता होती है।

>>

मैं इस तरह की समस्या तैयार करता हूं:
हमें इस तरह की एक सूची की आवश्यकता है, मानों के सेट का प्रत्येक तत्व पूरे मानचित्र में इसके अधिकतम मूल्य के बराबर या उससे अधिक है, इस सीमा को ध्यान में रखते हुए कि तत्वों को संबंधित स्पिल्ड तरल के क्रम में स्पष्ट रूप से स्थित होना चाहिए।

यह मैं इनपुट सूची से कर रहा हूं, एक नई सूची जिसके तत्व दिए गए रेंज में अज्ञात हो गए हैं (वर्तमान तत्व के आर 2 मान से अधिकतम मूल्य वी तक)
इनपुट पर, सूचियों की एक सूची; आउटपुट पर, मूल्यों की अधिकतम वितरण के साथ एक नई सूची,
जो "तरल पदार्थ संतुलन" की सीमा को पूरा करता है:

 checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St).

यह एक जनरेटर और एक ही समय में एक चेक दोनों है, यह संकेत दिया जाता है कि तत्व ऐसे सेट में हैं, और फिर धीरे-धीरे एक चेक लगाते हुए, यह सेट संकुचित है। आगे, कुछ रहता है, और इसे "चिह्नित" किया जा सकता है, अर्थात्। पूर्णांक मान सेट करें जो सभी बाधाओं के योग को पूरा करेगा। कॉलिंग लेबलिंग ([नीचे], FX2) भरने के लिए मजबूर करता है (संपर्क) ~~परिवर्तनशील~~ विशिष्ट मानों के साथ अज्ञात, और ऐसे कई विकल्प हो सकते हैं, लेकिन हम हमेशा बहुत पहले एक लेंगे, क्योंकि यह कहा गया था कि सभी चर खोज में नीचे की ओर बढ़ते हैं, उनके ऊपरी सीमा से, ये [नीचे] खोज विकल्प हैं।

और वहां आप इस तरह की जटिल सेटिंग्स देख सकते हैं:

16.2.1। चर चयन रणनीति
चर चयन रणनीति आपको यह निर्दिष्ट करने देती है कि कौन सा चर वर के बगल में लेबल किया गया है और इनमें से एक है:
बाईं ओर - वे में होने वाले क्रम में चर लेबल करें। यह डिफ़ॉल्ट है।
एफएफ पहले असफल। सबसे छोटे डोमेन के साथ सबसे बाईं ओर वाले चर को लेबल करें, ताकि इन्फैटेबिलिटी का जल्दी पता लगाया जा सके। यह अक्सर एक अच्छी रणनीति होती है जब पहले चर को चुने जाने के बाद के चर के लिए छोटे डोमेन होते हैं।
सबसे छोटे डोमेन वाले चरों के ffc, सबसे अधिक अवरोधों में भाग लेने वाले सबसे बाईं ओर अगला लेबल किया गया है। बाधा को लागू करने के लिए एक उपप्रकार निकालना होगा, इसलिए यह एक अच्छी रणनीति हो सकती है।
न्यूनतम बाईं चर का लेबल जिसकी निचली सीमा अगली सबसे कम है। ध्यान दें कि यह मिनट / 1 से अलग है, जो समाधान समाधान निर्धारित करता है और ऊपर पिछले अनुभाग में चर्चा की गई है। यह एक अच्छी रणनीति है यदि आप कुछ वैश्विक मूल्य को कम करने की कोशिश कर रहे हैं जो कि कम हो सकता है यदि विभिन्न चर हैं (उदाहरण के लिए एक न्यूनतम लागत समाधान)।
अधिकतम बाईं ओर वाला चर लेबल करें जिसका ऊपरी बाउंड सबसे आगे है। यह भी अधिकतम / 1 से भिन्न है। और वैश्विक मान को अधिकतम करने की कोशिश करते समय न्यूनतम के लिए सलाह अधिकतम पर लागू होती है।
16.2.2। मूल्य क्रम
मूल्य क्रम निम्न में से एक है:
variable चुने हुए चर के डोमेन के तत्वों को आरोही क्रम में आज़माएँ। यह डिफ़ॉल्ट है।
नीचे अवरोही क्रम में डोमेन तत्वों को आज़माएं।
जाहिर है, अगर आपके पास एक असममित वितरण मिला है, जैसे हमने ऊपर कुशलतापूर्वक लेबल करने के लिए प्रदर्शन किया है, तो पहले सामान्य क्रम में तत्वों को आज़माएं।
16.2.3। शाखापर रणनीति
शाखाओं में बंटी रणनीति निम्नलिखित में से एक है:
चरण प्रत्येक चर एक्स के लिए, एक्स = वी और एक्स # \ = वी के बीच एक विकल्प बनाया जाता है, जहां वी मूल्य आदेश विकल्पों द्वारा निर्धारित किया जाता है। यह डिफ़ॉल्ट है।
enum प्रत्येक चर X के लिए, X = V_1, X = V_2 आदि के बीच चयन किया जाता है, X के डोमेन के V_i के सभी मूल्यों के लिए। ऑर्डर मूल्य निर्धारण विकल्पों द्वारा निर्धारित किया जाता है।
bisect प्रत्येक चर X के लिए, X # = <M और X #> M के बीच एक विकल्प बनाया जाता है, जहाँ M, X के डोमेन का मध्य बिंदु है। इस विकल्प को चुनें यदि कई चर पूर्णांक की श्रेणी के बीच चयन करते हैं, तो एक मान, गणना मूल्यों के एक सेट के बीच एक के बजाय (जैसे प्रतिशत, बनाम ए = 0, बी = 1, सी = 2)

अब वास्तव में "संतुलित" क्या है जब डाला गया पानी सेल से सेल तक नहीं जाता है। यह तत्वों के प्रारंभिक क्रम का पत्राचार है। आप सोच सकते हैं कि कोशिकाओं को भरने से मूल परिदृश्य का आकार बरकरार रहेगा, जिसका मतलब है कि अगर दीवार थी, तो इसे शीर्ष पर पानी के साथ कवर किया जा सकता है, ताकि यह आवश्यक रूप से अपने सभी पड़ोसियों के बराबर हो जाए, या यदि यह पानी से ढकी हुई दीवार नहीं है ...

संतुलित स्थितियों पर विचार करें:
-यदि सेल में बाढ़ आ गई है, तो उसी के बगल में या उससे भी अधिक (अचानक यह दीवार है)।
-अगर सेल पड़ोसी के बराबर था, तो यह नए पड़ोसी के बराबर होना चाहिए।
और चरम मामले में, सेल ने अपना अर्थ नहीं बदला, और फिर भी उसके पास किस तरह के पड़ोसी थे:

 %   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %    , %        equ(C0,_,C,[U,L,R,D]):-C#>C0,C#=<U,C#=<R,C#=<L,C#=<D. equ(_,[],_,[]). equ(C0,[C0|T0],C,[C|T]):-equ(C0,T0,C,T). equ(C,_,C1,_):-C1#=C.

यह है कि आप कार्यक्रम में अपने दृष्टिकोण को कार्य में कैसे स्थानांतरित कर सकते हैं। निर्णय एल्गोरिथ्म के बारे में सोचना मेरे लिए आवश्यक नहीं है, परिणाम का सही विवरण प्रदान करना महत्वपूर्ण है, सभी प्रारंभिक बाधाओं (मूल्यों के सेट) को सही ढंग से सेट करना है। यह दृष्टिकोण बस लौटाया जा सकता है और लौटना के साथ सामान्य खोज के साथ "मिश्रित" हो सकता है। यह क्लासिक प्रोलॉग विधियों का उपयोग करने की तुलना में और भी अधिक घोषणात्मक कार्यक्रमों को तैयार करने का एक तरीका है।

मैं परीक्षण के एक सेट के साथ प्राप्त समाधान दूंगा:

 :- use_module(library(clpfd)). checks(X0,X2):- flatten(X0,FX), max_list(FX,Max),checks(Max,X0,X2), balns(X0,X2), flatten(X2,FX2), labeling([down],FX2). checks(_,[],[]). checks(_,[X],[X]). checks(_,[X,Z],[X,Z]). checks(V,[R1,R2,R3|T],[R1|St]) :- number(R2),!, R21 in R2..V, checks(V,[R21,R3|T],St). checks(V,[R1,R2,R3|T],[R1|St]) :- checks(V,R2,R21),checks(V,[R21,R3|T],St). %   balns([],[]). balns([_],[_]). balns([_,_],[_,_]). balns([B1,B2,B3|Tb],[R1,R2,R3|T]) :- blevel(B1,B2,B3,R1,R2,R3), balns([B2,B3|Tb],[R2,R3|T]). %     ,    33 blevel([],[],[],[],[],[]). blevel([_],[_],[_],[_],[_],[_]). blevel([_,_],[_,_],[_,_],[_,_],[_,_],[_,_]). blevel([_,U1,U2|Tu],[R,C,L|T],[_,B1,B2|Tb], [_,U10,U20|Tu0],[R0,C0,L0|T0],[_,B10,B20|Tb0]):- equ(C,[U1,L,R,B1],C0,[U10,L0,R0,B10]), blevel([U1,U2|Tu],[C,L|T],[B1,B2|Tb], [U10,U20|Tu0],[C0,L0|T0],[B10,B20|Tb0]). %    , %        equ(C0,_,C,[U,L,R,D]):-C#>C0,C#=<U,C#=<R,C#=<L,C#=<D. equ(_,[],_,[]). equ(C0,[C0|T0],C,[C|T]):-equ(C0,T0,C,T). equ(C,_,C1,_):-C1#=C. diffall(L0,L2,S):- flatten(L0,F0),sum_list(F0,S0), flatten(L2,F2),sum_list(F2,S2), S is S2-S0. sums(X,S):-checks(X,X1),!,diffall(X,X1,S). %unit-tests framework assert_are_equal(Goal, false):-get_time(St),not(Goal),!,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, true):- get_time(St),Goal, !,get_time(Fin),Per is round(Fin-St),writeln(Goal->ok:Per/sec). assert_are_equal(Goal, Exp):-writeln(Goal->failed:expected-Exp). :-assert_are_equal(sums([[1,4,3,1,3,2],[3,2,1,3,2,4],[2,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[1,3,3,1,3,2],[3,2,1,3,2,3],[3,3,3,2,3,1]],4),true). :-assert_are_equal(sums([[12,13,1,12],[13,4,13,12],[13,8,10,12],[12,13,12,12],[13,13,13,13]],14),true). :-assert_are_equal(sums([[2,3,4],[5,6,7],[8,9,10],[11,12,13],[14,15,16]],0),true). :-assert_are_equal(sums([[18,2,3],[4,5,6],[7,8,9]],0),true). :-assert_are_equal(sums([[3,5,5],[5,4,5],[5,5,5]],1),true). :-assert_are_equal(sums([[5,5,5,1],[5,1,1,5],[5,1,5,5],[5,2,5,8]],3),true). :-assert_are_equal(sums([[2,2,2],[2,1,2],[2,1,2],[2,1,2]],0),true). :-assert_are_equal(sums([[17,2,3,4,5,6,7,8,9,10]],0),true). :-assert_are_equal(sums([[9,9,9,9,9],[9,2,1,2,9],[9,2,8,2,9],[9,2,3,2,9],[9,9,9,9,9]],57),true). :-assert_are_equal(sums([[78,16,94,36],[87,93,50,22],[63,28,91,60],[64,27,41,27],[73,37,12,69],[68,30,83,31],[63,24,68,36]],44),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[5,5,5],[5,1,5],[5,5,5]],4),true). :-assert_are_equal(sums([[5,5,5],[5,1,5],[5,1000,6]],4),true). :-assert_are_equal(sums([[5,8,7,7],[5,2,1,5],[7,1,7,1],[8,9,6,9],[9,8,9,9]],12),true). :-assert_are_equal(sums([[11,21,31],[81,9,41],[17,61,51]],12),true). :-assert_are_equal(sums([[3,3,4,4,4,2],[3,1,3,2,1,4],[7,3,1,6,4,1]],5),true). :-assert_are_equal(sums([[14,17,18,16,14,16],[17,3,10,2,3,8],[11,10,4,7,1,7],[13,7,2,9,8,10],[13,1,3,4,8,6],[20,3,3,9,10,8]],25),true). :-assert_are_equal(sums([[14,17,12,13,20,14],[12,10,5,8,9,5],[16,1,4,7,2,1],[17,4,3,1,7,2],[16,6,5,8,7,6],[17,10,4,8,5,6]],12),true).

और अधिक परीक्षण

 :-assert_are_equal(sums([[13,16,15,18,15,15],[14,1,8,9,7,9],[19,5,4,2,5,10],[13,1,7,9,10,3],[17,7,5,10,6,1],[15,9,8,2,8,3]],36),true). :-assert_are_equal(sums([[18,13,13,17,12,11],[17,2,6,10,5,10],[11,10,2,8,8,2],[12,6,10,8,8,7],[18,4,7,6,7,4],[20,5,9,2,3,10]],18),true). :-assert_are_equal(sums([[14,20,11,19,19,16],[11,10,7,4,9,6],[17,2,2,6,10,9],[15,9,2,1,4,1],[15,5,5,5,8,7],[14,2,8,6,10,7]],11),true). :-assert_are_equal(sums([[19383,10886,12777,16915,17793,18335,15386,10492,16649,11421],[12362,27,8690,59,7763,3926,540,3426,9172,5736],[15211,5368,2567,6429,5782,1530,2862,5123,4067,3135],[13929,9802,4022,3058,3069,8167,1393,8456,5011,8042],[16229,7373,4421,4919,3784,8537,5198,4324,8315,4370],[16413,3526,6091,8980,9956,1873,6862,9170,6996,7281],[12305,925,7084,6327,336,6505,846,1729,1313,5857],[16124,3895,9582,545,8814,3367,5434,364,4043,3750],[11087,6808,7276,7178,5788,3584,5403,2651,2754,2399],[19932,5060,9676,3368,7739,12,6226,8586,8094,7539]],79058),true). :-assert_are_equal(sums([[10795,10570,11434,10378,17467,16601,10097,12902,13317,10492],[16652,756,7301,280,4286,9441,3865,9689,8444,6619],[18440,4729,8031,8117,8097,5771,4481,675,709,8927],[14567,7856,9497,2353,4586,6965,5306,4683,6219,8624],[11528,2871,5732,8829,9503,19,8270,3368,9708,6715],[16340,8149,7796,723,2618,2245,2846,3451,2921,3555],[12379,7488,7764,8228,9841,2350,5193,1500,7034,7764],[10124,4914,6987,5856,3743,6491,2227,8365,9859,1936],[11432,2551,6437,9228,3275,5407,1474,6121,8858,4395],[16029,1237,8235,3793,5818,4428,6143,1011,5928,9529]],68900),true). :-assert_are_equal(sums([[18776,12404,14443,15763,14613,14538,18606,16840,12904,14818],[15128,688,7369,7917,9917,6996,3324,7743,9470,2183],[18490,5499,9772,6725,5644,5590,7505,8139,2954,9786],[17669,8082,8542,8464,197,9507,9355,8804,6348,8611],[13622,7828,9299,7343,5746,5568,4340,5422,3311,3810],[17605,1801,5661,3730,4878,1305,9320,8736,9444,8626],[18522,3465,6708,3416,8282,3258,2924,7637,2062,5624],[12600,2036,3452,1899,9379,5550,7468,71,973,7131],[13881,4930,8933,5894,8660,163,7199,7981,8899,2996],[12959,3773,2813,9668,7190,1095,2926,6466,5084,1340]],61413),true). :-assert_are_equal(sums([[12090,17684,13376,15542,15936,19107,17445,19756,19179,18418],[16887,9412,3348,2172,1659,2009,2336,5210,6342,7587],[18206,9301,7713,7372,5321,1255,4819,4599,7721,9904],[15939,9811,3940,5667,1705,6228,1127,9150,5984,6658],[13920,9224,2422,7269,1396,4081,5630,84,9292,1972],[17672,3850,7625,5385,1222,9299,6640,6042,3898,713],[12298,6190,524,2590,8209,8581,8819,9336,7732,1155],[15994,8004,379,4769,5273,1776,8850,7255,1860,8142],[15579,5884,1993,3205,7621,9567,2504,613,1961,2754],[11326,4259,8944,8202,3202,3506,6784,2021,2842,868]],89383),true). :-assert_are_equal(sums([[19528,15189,18872,19908,19958,10498,18036,18808,17753,16248],[13303,3333,2133,1648,2890,9754,7567,1746,368,9529],[14500,8046,3788,9797,6249,6990,3303,3033,5363,2497],[10253,4892,7686,9125,1152,3996,5975,9188,9157,3729],[15436,2460,3414,3921,460,6304,28,8027,8050,6748],[17556,8902,4794,7697,8699,1043,1039,2002,428,6403],[14500,681,7647,8538,6159,5151,2535,2134,4339,1692],[12215,6127,504,5629,49,964,8285,6429,5343,6335],[13177,2900,5238,7971,6949,289,5367,7988,2292,5795],[10743,3144,2829,8390,1682,5340,3541,569,3826,4232]],100439),true).

साइट से ये परीक्षण किए गए, केवल पहले 30 टुकड़े। परिणाम उत्कृष्ट है, समस्या हल हो गई है, और जल्दी से भी, हर समय एक सेकंड तक।

आप देख सकते हैं ...

निष्कर्ष के रूप में

घोषणात्मक प्रोग्रामिंग में कार्य की एक विस्तृत औपचारिकता शामिल है, और सॉल्वर सबसे प्रभावी समाधान की तलाश करेगा जो शर्तों को पूरा करेगा।

विषय में थोड़ा गहरा, आप मिनीज़िंक खोल सकते हैं, एक प्रोग्रामिंग भाषा जिसमें यह प्रतिमान एम्बेडेड है। उन्होंने कई अर्थों का संकेत दिया, प्रतिबंध और संकेत के जवाब दिए। वे सुडोकू , मैपिंग कलरिंग टास्क, शेड्यूलिंग वर्क , रिसोर्स प्रॉब्लम, शेड्यूलिंग को हल करते हैं । मैं प्रशिक्षित करने का सुझाव देता हूं ...

प्रोलॉग का उपयोग करना

कार्य यह है कि इसे कैसे गति दी जाए?

निष्कर्ष के रूप में

More articles: