अराजकता के गणितीय मॉडल

परिचय

हैबर ने पहले ही लेखों में अराजकता सिद्धांत पर चर्चा की [1,2,3]। अराजकता सिद्धांत के निम्नलिखित पहलुओं को इन लेखों में माना जाता है: चुआ जनरेटर का सामान्यीकृत आरेख; लोरेंत्ज़ सिस्टम की गतिशीलता को मॉडलिंग करना; लॉरेंत्ज़, रोस्लर, रिकिटेक और नोज़-हूवर आकर्षित करने वाले तर्क एकीकृत सर्किट द्वारा क्रमादेशित हैं।

हालांकि, अराजकता सिद्धांत की तकनीकों का उपयोग जैविक प्रणालियों को मॉडल करने के लिए भी किया जाता है, जो निस्संदेह, उन सभी की सबसे अराजक प्रणालियों में से एक हैं जिनकी कल्पना की जा सकती है। डायनेमिक इक्वलाइजेशन सिस्टम का उपयोग आबादी और महामारी की वृद्धि से लेकर अतालतापूर्ण हृदय की धड़कन [4] तक सब कुछ मॉडल करने के लिए किया गया था।

वास्तव में, लगभग किसी भी अराजक प्रणाली का मॉडल तैयार किया जा सकता है - प्रतिभूति बाजार घटता उत्पन्न करता है, जिसका विश्लेषण आसानी से किया जा सकता है, जो कि अजीब आकर्षित करने वालों का उपयोग करके किया जाता है, नग्न कान से विश्लेषण करने पर एक लीक टैप से बूंदों को छोड़ने की प्रक्रिया यादृच्छिक होती है, लेकिन अगर एक अजीब आकर्षण के रूप में चित्रित किया जाता है, तो यह खुलता है। एक अलौकिक क्रम जिसे पारंपरिक तरीकों से उम्मीद नहीं की जा सकती थी।

इस लेख का उद्देश्य पाइथन में लिखित सरल सहज कार्यक्रमों के आधार पर गणितीय मॉडल के चित्रमय दृश्य के साथ जैविक आबादी की संख्या में वृद्धि और यांत्रिक प्रणालियों में चक्र को दोगुना करने के उदाहरण का उपयोग करके अराजकता के सिद्धांत की जांच करना है।

लेख पढ़ाने के उद्देश्य से लिखा गया था, लेकिन यह भी एक पाठक को बिना किसी प्रोग्रामिंग अनुभव के साथ उपरोक्त कार्यक्रमों का उपयोग करने की अनुमति देगा, जो कि अराजकता की घटनाओं के विषय पर स्वतंत्र रूप से मॉडलिंग की अधिकांश नई शैक्षणिक समस्याओं को हल कर सकता है।

जैविक आबादी की संख्या के विकास के उदाहरण पर चक्र और अराजकता की अवधि को दोगुना करना

आइए लॉजिस्टिक डिफरेंशियल समीकरण को देखते हुए शुरू करें, जो कि जैविक आबादी की संख्या में घातीय वृद्धि के बजाय एक सीमित मॉडल है:

$$$\ frac {dN} {dt} = aN-bN ^ {2}, (a, b> 0)। (१)$

यह ऐसा समीकरण है जो कुछ आबादी के व्यवहार के विदेशी और अप्रत्याशित पैटर्न की भविष्यवाणी कर सकता है। वास्तव में, (1) के अनुसार, के लिए $$$t \ rightarrow + \ infty$ जनसंख्या का आकार सीमा के बराबर / b तक पहुंचता है।

लॉजिस्टिक अंतर समाधान के संख्यात्मक समाधान के लिए, आप सरलतम एल्गोरिथ्म का उपयोग कर सकते हैं, समय कदम के संख्यात्मक मान के साथ, ले $$$t_ {n + 1} = t_ {n} + h$ , तो समाधान (1) निम्नलिखित संबंध को बार-बार लागू करके प्राप्त किया जा सकता है:

$$$N_ {n + 1} = N_ {n} + (aN_n-bN {_ {n}} ^ {2}) h।$ (2)

हम परिमित अंतर में लॉजिस्टिक समीकरण के रूप में समीकरण (2) का प्रतिनिधित्व करते हैं:

$$$N_ {n + 1} = rN_ {n} -sN {_ {n}} ^ {2}$ । (3)

जहाँ: r = 1 + आह और s = bh ।
(3) में प्रतिस्थापन $$$N_ {n} = \ frac {r} {s} x_ {n}$ हमें पुनरावृत्ति सूत्र मिलता है:

$$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ , (4)

संबंध (3) द्वारा दिए गए मूल्यों की गणना, हम एक अनुक्रम उत्पन्न कर सकते हैं $$$x_ {1}, x_ {2}, x_ {3}, .....$
आबादी की संख्या के अधिकतम मूल्य जो पर्यावरण दिए गए समय पर समर्थन करेंगे $$$t_ {1}, t_ {2}, t_ {3}$ ।

हम मानते हैं कि जनसंख्या के आकार के एक हिस्से को व्यक्त करने वाले भिन्नों का एक सीमित मूल्य है:

$$$x _ {\ infty} = \ lim_ {n \ to \ infty} x_ {n}$ , (5)।

हम जांच करेंगे कि यह कैसे निर्भर करता है $$$x _ {\ infty}$ समीकरण (4) में विकास पैरामीटर आर से। ऐसा करने के लिए, पायथन में, हम एक प्रोग्राम लिखते हैं, जिसके साथ शुरू होता है $$$x_ {1} = $ 0.$ r = 1.5; 2.0; 2.5 के लिए कई सौ पुनरावृत्तियों ( n = 200 ) पर परिणामों की गणना करता है ;


कार्यक्रम का परिणाम (परिणामों के उत्पादन को कम करने के लिए, पहले तीन और अंतिम चार मान दिए गए हैं):

  nr=1,5 r=2,0 r=2,5 0 0.5000 0.5000 0.5000 1 0.3750 0.5000 0.6250 2 0.3516 0.5000 0.5859 . . . 197 0.3333 0.5000 0.6000 198 0.3333 0.5000 0.6000 199 0.3333 0.5000 0.6000 200 0.3333 0.5000 0.6000 

असतत मॉडल के विश्लेषण से पता चलता है कि r = 1.5; 2.0; 2.5 के लिए पुनरावृत्तियों की संख्या में वृद्धि, मान $$$x_ {n}$ स्थिर और सीमा के लगभग बराबर हो जाता है $$$x _ {\ infty}$ , जो संबंध (5) से निर्धारित होता है। इसके अलावा, आर के दिए गए मूल्यों के लिए , मात्रा $$$x _ {\ infty}$ समान रूप से बराबर $$$x _ {\ infty} = 0.3333; 0.5000; $ 0.600$ ।
हम आर = 3.1; 3.25; 3.5 और पुनरावृत्तियों की संख्या n = 1008 बढ़ाते हैं, इसके लिए हम कार्यक्रम में निम्नलिखित परिवर्तन करते हैं:


कार्यक्रम का परिणाम (परिणामों के उत्पादन को कम करने के लिए, पहले चार और अंतिम आठ मान दिए गए हैं):

  nr=3,1 r=3,25 r=3,5 0 0.5000 0.5000 0.5000 1 0.7750 0.8125 0.8750 2 0.5406 0.4951 0.3828 3 0.7699 0.8124 0.8269 . . . 1000 0.5580 0.4953 0.5009 1001 0.7646 0.8124 0.8750 1002 0.5580 0.4953 0.3828 1003 0.7646 0.8124 0.8269 1004 0.5580 0.4953 0.5009 1005 0.7646 0.8124 0.8750 1006 0.5580 0.4953 0.3828 1007 0.7646 0.8124 0.8269 

उपरोक्त आंकड़ों के अनुसार, एक ही सीमित आबादी के पास स्थिर होने के बजाय, समय के परिवर्तन के साथ जनसंख्या का आंशिक भाग दो भिन्नताओं के बीच उतार-चढ़ाव करता है। आर = 3.1 की तुलना में, आर = 3.25 डबल्स के लिए चक्र अवधि, और आर = 3.5 चार बार के लिए।


कार्यक्रम का परिणाम:



पुनरावृत्ति अवधि को दोगुना करने के लिए, $$$x_ {n + 1} = rx_ {n} (1-x_ {n})$ व्यापक रूप से जाना जाता है। जब विकास दर का मान r = 3.56 से अधिक हो जाता है, तो अवधि का दोगुना बढ़ जाता है और चरम अराजकता बिंदु r = 3.57 पर पहले से ही उत्पन्न हो जाती है। अराजकता की शुरुआत को प्रदर्शित करने के लिए, हम निम्नलिखित कार्यक्रम का उपयोग करते हैं:


कार्यक्रम का परिणाम:

  nr=3,57 1000 0.4751 1001 0.8903 1002 0.3487 1003 0.8108 1004 0.5477 1005 0.8844 1006 0.3650 1007 0.8275 1008 0.5096 1009 0.8922 1010 0.3434 1011 0.8050 1012 0.5604 1013 0.8795 1014 0.3784 1015 0.8397 

हम विकास पैरामीटर आर पर पुनरावृत्ति व्यवहार की निर्भरता को देखने के लिए एक कार्यक्रम लिखेंगे। अंतराल में आर के प्रत्येक मूल्य के लिए $$$a \ leqslant r \ leqslant b$ स्थिरता प्राप्त करने के लिए 1000 पुनरावृत्तियों का प्रदर्शन किया जाता है। फिर, पुनरावृत्तियों के परिणामस्वरूप प्राप्त प्रत्येक 250 मान को ऊर्ध्वाधर अक्ष के साथ प्लॉट किया जाता है, अंक ( आर, एक्स ) बनाते हुए:


एक आरेख के रूप में परिणाम:



परिणामी ग्राफ़ को "शाखा आरेख" कहा जाता है, जो आपको यह निर्धारित करने की अनुमति देता है कि क्या दिए गए r मान एक चक्र या अराजकता से मेल खाती है। जनसंख्या के आकार का एकमात्र मूल्य मूल्य के लिए निर्धारित होता है $$$r \ लगभग 3$ फिर 2 से पीरियड के साथ एक चक्र $$$r \ लगभग 3.4$ , फिर 4 की अवधि के साथ एक चक्र, फिर अराजकता के लिए तेजी से दृष्टिकोण के साथ 8 आगे की अवधि के साथ एक चक्र।

यह ध्यान दिया जाना चाहिए कि ग्राफ पर अनफिल्टर्ड स्पेस के ऊर्ध्वाधर क्षेत्र आर = 3.6 और आर = 3.8 के बीच आर = 3.8 और आर = 3.9 के बीच के क्षेत्र आर = 3.6 और आर = 3.7 हैं । जहां चक्रीय क्रम पिछले अराजकता से लौटता है।
क्षेत्र में 3 की अवधि के साथ एक चक्र की उपस्थिति पर विचार करने के लिए $$$3.8 \ leqslant r \ leqslant $ 3.$ पिछले कार्यक्रम में परिवर्तन करें:


कार्यक्रम का परिणाम:



अवधि 3 का चक्र बिंदु r = 3.83 के आसपास के क्षेत्र में प्रकट होता है, और फिर क्रमिक रूप से चक्र 6,12,24 में विभाजित होता है। अवधि 3 के साथ एक चक्र का अस्तित्व किसी भी अन्य परिमित अवधि के चक्रों की उपस्थिति का अर्थ है, साथ ही साथ बिना किसी अवधि के अराजक चक्र भी।

शाखा आरेख आपको पैरामीटर में एक सहज बदलाव के साथ सिस्टम के विकास का पालन करने की अनुमति देता है। पैरामीटर के एक निश्चित मूल्य के साथ, मकड़ी आरेख (लामेरा आरेख) अंक कक्षाओं को ट्रेस करने की अनुमति देता है।

स्पाइडर आरेख का निर्माण आपको विभिन्न प्रभावों की पहचान करने की अनुमति देता है जो शाखा आरेख पर अदृश्य हैं। आइए एक कार्यक्रम लिखें:


लामेरा चित्र:

मैकेनिकल सिस्टम में दोहरीकरण

एक विभेदक समीकरण पर विचार करें जो मॉडल एक गैर-रैखिक वसंत पर किसी दिए गए द्रव्यमान के एक भौतिक बिंदु के कंपित कंपन को मुक्त करता है, जिस पर गति द्वारा गति निर्धारित की जाती है।

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = 0$ (6)

समीकरण (6) में, शब्द kx किसी दिए गए द्रव्यमान के भौतिक बिंदु पर लागू एक रैखिक वसंत के बल का प्रतिनिधित्व करता है, और शब्द $$$\ बीटा x ^ {3}$ वसंत की वास्तविक ग़ैरबराबरी का प्रतिनिधित्व करता है।

यदि कोई बल मुक्त दोलनों (6) की प्रणाली पर कार्य करता है, तो उस द्रव्यमान के भौतिक बिंदु का विस्थापन, जिस पर यह बल लगाया जाता है, को मजबूर दोलनों के लिए डफिंग अंतर समीकरण द्वारा वर्णित किया जाता है:

$$$mx ^ {''} + cx ^ {'} + kx + \ beta x ^ {3} = F_ {0} cos \ omega t$ (7)

इसमें शामिल अधिकांश मापदंडों के लिए समीकरण (7) संख्यात्मक रूप से हल किया गया है। समीकरण के अनुसार गणितीय मॉडल के लिए यांत्रिक प्रणाली (7) को चित्र में दिखाया गया है:



दी गई प्रणाली की एक विशेषता यह है कि वसंत के बजाय एक लचीली धातु के धागे का उपयोग किया जाता है, जो एक ऊर्ध्वाधर विमान में दोलन करता है, जिसके लिए हुक निरंतर k नकारात्मक है। इस योजना में, स्थिर संतुलन (ए) और (सी) के बिंदु, और अस्थिर संतुलन के बिंदु (बी)।

जब किसी भौतिक बिंदु को स्थिति (b) से विस्थापित किया जाता है, तो उस पर कार्य करने वाला बल प्रतिकारक होता है। यदि आवधिक बल, उदाहरण के लिए, दोलन चुंबकीय क्षेत्र द्वारा बनाया गया है, तो आंशिक रूप से वायु प्रतिरोध से भीगा हुआ है। फिर, समीकरण (7) निम्नलिखित घटकों के साथ एक भौतिक बिंदु के क्षैतिज विस्थापन x (t) के लिए एक स्वीकार्य गणितीय मॉडल है $$$k <0, c> 0, \ बीटा> 0$ ।

इस तरह के नॉनलाइनर सिस्टम के व्यवहार का अध्ययन करने के लिए, हम लेते हैं $$$k = -1, m = c = \ beta = \ omega = 1$ तब अंतर समीकरण (7) रूप लेता है:

$$$x ^ {''} + x ^ {'} - x + x ^ {3} = F_ {0} cos (t)$ , (8)

हम प्रारंभिक परिस्थितियों में समीकरण (8) के संख्यात्मक एकीकरण के लिए एक कार्यक्रम लिखते हैं $$$x (0) = 1, x ^ {'} (0) = 0$ मैदान में $$$100 \ leqllant t \ leqslant 200$ और निम्नलिखित आयाम मूल्यों में से प्रत्येक के लिए $$$F_ {0} = 0.6; 0.7; 0.75; 0.8$ , और प्रत्येक मामले में, विमानों के लिए समाधान की साजिश है $$$x (t), x ^ {'} (t)$ और $$$t, x (t)$ :


कार्यक्रम के परिणामस्वरूप चार्ट





अराजकता को दोगुना करने की अवधि से यह संक्रमण उदाहरण के लिए इसी भौतिक पैरामीटर में परिवर्तन के जवाब में एक गैर-यांत्रिक तंत्र के सामान्य व्यवहार को दर्शाता है: $$$k, m, c, \ beta, \ omega, F_ {0}$ । ऐसी घटनाएं रैखिक यांत्रिक प्रणालियों में नहीं होती हैं।

आकर्षण करने वाला लोरेंज

मजबूर दोलनों के लिए डफिंग समीकरण में प्रतिस्थापन (7) अंतर समीकरणों के दो-आयामी nonlinear प्रणाली की ओर जाता है, जिसे पिछली सूची में दिखाया गया था। मौसम संबंधी समस्याओं पर लागू अंतर समीकरणों की एक त्रि-आयामी nonlinear प्रणाली को ई.एन. लोरेन्ज:

$$$\ frac {dx} {dt} = - sx + sy,$
$$$\ frac {डाई} {dt} = - xz + rx-y,$ (9)
$$$\ frac {dz} {dt} = xy-dz$

सिस्टम का समाधान (9) तीन विमानों में से एक पर प्रक्षेपण में सबसे अच्छा देखा जाता है। हम मापदंडों के मूल्यों के लिए संख्यात्मक एकीकरण का एक प्रोग्राम लिखते हैं b = \ frac {8} {3}, s = 10, r = 28 और प्रारंभिक शर्तें x (0) = - 8, y (0) = 8, z (0) = 27 : 27


कार्यक्रम का परिणाम:



समय के साथ ग्राफ़ पर छवि को ध्यान में रखते हुए, यह माना जा सकता है कि बिंदु P (x (t), y (t), z (t) बिंदु, दाएं या बाएं यादृच्छिक संख्याएँ बनाता है। लोरेंज प्रणाली के मौसम संबंधी अनुप्रयोग के लिए, स्पष्ट दिनों की एक यादृच्छिक संख्या के बाद, बारिश के दिनों की एक यादृच्छिक संख्या इस प्रकार है।

थोड़ा अलग प्रारंभिक स्थितियों के लिए xyz विमान में लोरेंत्ज़ आकर्षित करने वाले के मानचित्रण के लिए एक कार्यक्रम पर विचार करें:


कार्यक्रम के परिणाम निम्नलिखित ग्राफ में दिखाए गए हैं:





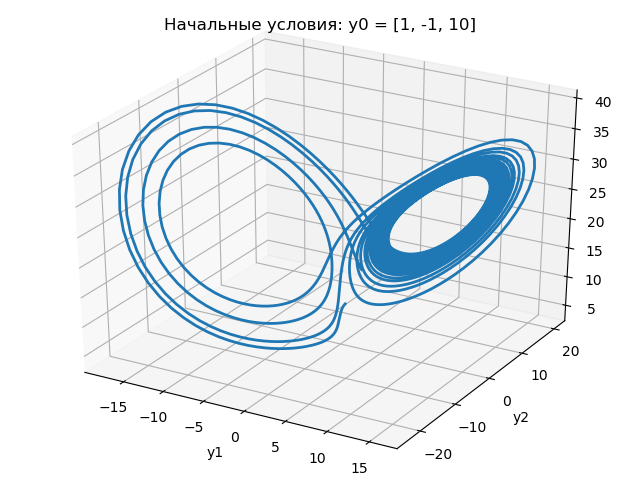
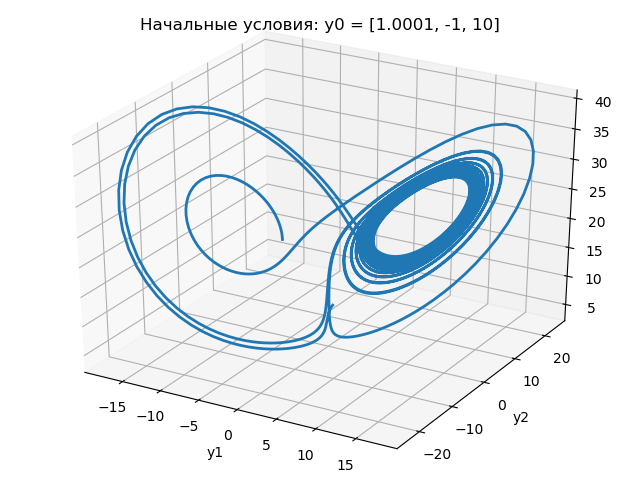
उपरोक्त ग्राफ़ से यह निम्नानुसार है कि 1.0 से 1.0001 के लिए प्रारंभिक स्थिति में परिवर्तन नाटकीय रूप से लॉरेंटज़ के आकर्षण में परिवर्तन की प्रकृति को बदलता है।

रोसलर प्रणाली

यह एक बहुत ही गहनता से अध्ययन किया जाने वाला अरेखीय त्रि-आयामी प्रणाली है:
$$$\ frac {dx} {dt} = - y-z,$
$$$\ frac {डाई} {dt} = x- \ अल्फा वाई,$ (10)
$$$\ frac {dz} {dt} = b + x (x-c)$

हम प्रारंभिक मानकों x (0) = 0, y (0) = 0, z (0) = 0 : के तहत प्रणाली के संख्यात्मक एकीकरण के लिए एक कार्यक्रम लिखेंगे।


कार्यक्रम का परिणाम:



प्लेन में, रॉसलर का टेप लूप की तरह दिखता है, लेकिन अंतरिक्ष में यह मोएबियस टेप की तरह मुड़ता है।

निष्कर्ष

अराजकता की घटनाओं को प्रदर्शित करने के लिए, एक उच्च-स्तरीय पायथन प्रोग्रामिंग भाषा में सरल और सहज कार्यक्रम प्रस्तुत किए जाते हैं, जो इस विषय पर नई परियोजनाओं को अपग्रेड करना आसान है। लेख में शैक्षिक और पद्धतिगत ध्यान दिया गया है और इसे सीखने की प्रक्रिया में उपयोग किया जा सकता है।

संदर्भ

1. अराजकता के बारे में थोड़ा और इसे कैसे बनाएं
2. लोरेंज आकर्षित करने वाले पर एक महत्वपूर्ण नज़र
3. FPGA कैओस जेनरेटर
4. विभेदक समीकरण और सीमा मूल्य की समस्याएं: मॉडलिंग और गणितज्ञ, मेपल और MATLAB का उपयोग करके गणना। तीसरा संस्करण ।: प्रति। अंग्रेजी से - एम।: एलएलसी “आई.डी. विलियम्स, 2008. - 1104 पी .: बीमार। - पराल। तैसा। अभियांत्रिकी।