biquaternions

यदि आप इस लेख को खोलते हैं, तो आप शायद पहले से ही quaternions के बारे में सुनते हैं, और शायद उन्हें अपने डिजाइनों में भी उपयोग करें। लेकिन यह उच्च स्तर पर उठने का समय है - द्विभाजनों के लिए।

यह लेख उनके साथ संबंधों और संचालन के बारे में बुनियादी अवधारणा देता है। द्विभाजनों के साथ काम करने की बेहतर समझ के लिए, कैनवस का उपयोग करके जावास्क्रिप्ट में एक स्पष्ट उदाहरण दिखाया गया है।

निर्धारण biquaternion

Biquaternion एक हाइपरकम्पलेक्स संख्या है, जिसका आयाम 8. है। अंग्रेजी भाषा के लेखों और साहित्य में उन्हें "दोहरी चतुर्भुज" कहा जाता है, और रूसी-भाषा के साहित्य में "दोहरी चतुर्भुज" या "जटिल पैतृक" नाम भी हैं।

चतुर्भुज से मुख्य अंतर यह है कि चतुर्धातुक अंतरिक्ष में वस्तु के उन्मुखीकरण का वर्णन करता है, और द्विअर्थी भी अंतरिक्ष में वस्तु की स्थिति का वर्णन करता है।

Bateraternion को दो उद्धरणों के रूप में दर्शाया जा सकता है:

$$

$$\ widetilde {\ textbf {q}} = \ start {bmatrix} \ textbf {q} _1 \\ \ textbf {q} _2 \ end {bmatrix},$$

$$$\ textbf {q} _1$ - वास्तविक भाग, अंतरिक्ष में वस्तु के उन्मुखीकरण को निर्धारित करता है;
$$$\ textbf {q} _2$ - दोहरे भाग, अंतरिक्ष में वस्तु की स्थिति निर्धारित करता है।

द्विवचन को जटिल चतुर्भुज भी कहा जाता है, इस मामले में इसे एक चतुर्भुज के रूप में दर्शाया गया है, जिनमें से प्रत्येक घटक एक दोहरी संख्या है (जटिल के साथ भ्रमित नहीं होना)। दोहरी संख्या $$$A = a_1 + \ epsilon a_2$ जहाँ $$$a_1$ और $$$a_2$ वास्तविक संख्या हैं, और $$$\ epsilon$ - क्लिफर्ड प्रतीक (जटिलता), संपत्ति रखने $$$\ epsilon ^ 2 = 0$ । हम गणित में आगे नहीं बढ़ेंगे, क्योंकि हम लागू भाग में अधिक रुचि रखते हैं, इसलिए, आगे हम द्विभुज को दो चतुर्भुज के रूप में मानेंगे।

द्विआधारी की ज्यामितीय व्याख्या

चतुर्धातुक के साथ सादृश्य द्वारा, जिसके साथ आप ऑब्जेक्ट के ओरिएंटेशन को सेट कर सकते हैं, बाइकेटरियन भी स्थिति सेट कर सकते हैं। यानी अंतरिक्ष में एक ही समय में दो मान सेट करता है - अंतरिक्ष में वस्तु की स्थिति और अभिविन्यास। यदि हम उन्हें गतिकी में मानते हैं, तो द्विभाजन दो मात्राओं को परिभाषित करता है - गति का रैखिक वेग और वस्तु के रोटेशन का कोणीय वेग। नीचे दिया गया आंकड़ा द्विआधारी के ज्यामितीय अर्थ को दर्शाता है।



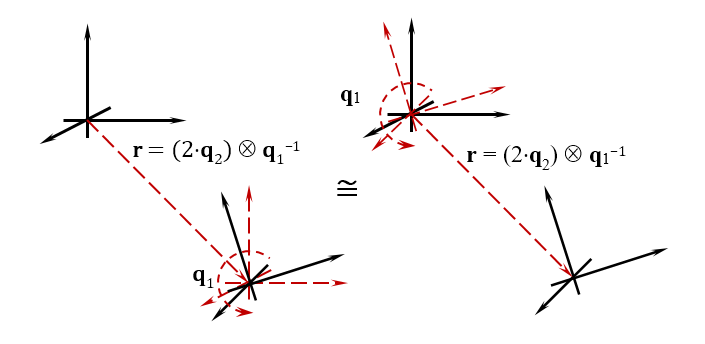
गेम डेवलपर्स को पता है कि प्लेइंग स्पेस में किसी ऑब्जेक्ट की स्थिति और ओरिएंटेशन सेट करने के लिए, रोटेशन मैट्रिसेस और विस्थापन मैट्रिसेस का उपयोग किया जाता है, और, जिस क्रम में आप उन्हें लागू करते हैं, उसके आधार पर, ऑब्जेक्ट की अंतिम स्थिति का परिणाम अलग होता है। उन लोगों के लिए जो आंदोलन को अलग-अलग कार्यों में विभाजित करने के आदी हैं, वे नियम के साथ काम करने के लिए स्वीकार करते हैं: पहले हम ऑब्जेक्ट को स्थानांतरित करते हैं, फिर हम इसे घुमाते हैं। वास्तव में, आप इन दो आंदोलनों को एक एकल संख्या के साथ वर्णन कर रहे हैं, भले ही एक जटिल हाइपरप्लोमक्स हो।

स्केलर विशेषताओं

मुख्य अदिश विशेषताओं पर विचार करें। यहां इस तथ्य पर ध्यान देना आवश्यक है कि वे साधारण वास्तविक संख्याएं नहीं लौटाते हैं, बल्कि दोहरे।

1. बाइकरनेशन का मानदंड

$$

$$\ _। \ n चौड़ी {\ textbf {q}} \ | = \ | \ textbf {q} _1 \ | + \ epsilon (q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2)$$

2. द्विभाजन मॉड्यूल

$$

$$| \ widetilde {\ textbf {q}} | = | \ textbf {q} _1 | + \ epsilon \ frac {q_ {1_0} q_ {2_0} + \ textbf {q} _1 ^ T \ textbf {q} _2} {| \ textbf {q} _1}$$

मूल संचालन

विचित्रताओं के साथ काम करने के बुनियादी कार्यों पर विचार करें। जैसा कि आप देख सकते हैं, वे quaternions के साथ समान संचालन के समान हैं।

1. द्विअर्थी युग्मन

$$

$$\ wideetilde {\ textbf {q}} ^ * = \ start {bmatrix} \ textbf {q} _1 ^ * \\ \ textbf {q} _2 ^ * \ end {bmatrix}$$

2. द्विभाजन जोड़ और घटाव

$$

$$\ widetilde {\ textbf {q}} \ pm \ widetilde {\ textbf {p}} = \ start {bmatrix} \ textbf {q} _1 \ pm \ textbf {p} _1 \\ \ textbf {q} _2 \ _ \ _ pm \ textbf {p} _2 \ end {bmatrix}$$

जुदाई और जोड़-घटाव कम्यूटेटिव है (शब्दों को आपस में जोड़ा जा सकता है)।

3. वास्तविक संख्या का बहुवचन द्वारा गुणा

$$

$$a \ widetilde {\ textbf {q}} = \ widetilde {\ textbf {q}} a = \ start {bmatrix} a \ textbf {q} _1 \\ a \ textbf {q} _2 \ end {bmatrix}$$

4. द्विअर्थी गुणन

$$

$$\ wideetilde {\ textbf {q}} \ otimes \ widetilde {\ textbf {p}} = \ start {bmatrix} \ textbf {q} _1 \ otimes \ textbf (p) _1 \\ \ textbf {q} _1 \ _ \ _ otimes \ textbf {p} _2 + \ textbf {q} _2 \ otimes \ textbf {p} _1 \ end {bmatrix}$$

Biquaternion गुणा गैर-कम्यूटेटिव है (कारकों के क्रम में बदलाव के साथ, biquaternion गुणन का परिणाम अलग है)।

यह ऑपरेशन मुख्य रूप से एक है जब बाइकेटरनियन्स के साथ काम करते हैं और एक भौतिक अर्थ को वहन करते हैं, अर्थात्, द्विभाजक गुणन का परिणाम दो द्विभाजनों के घुमाव और रैखिक आंदोलनों को जोड़ने का संचालन है।

5. विचित्रता का उलटा

$$

$$\ Widetilde {\ textbf {q}} ^ {- 1} = \ frac {\ widetilde {\ textbf {q}} ^ *}} \ {| \ wideetilde {\ textbf {q}}$$

अभिविन्यास कोणों और स्थिति वेक्टर के माध्यम से द्विबीजपत्री का निर्धारण

सबसे पहले, हम समन्वय प्रणालियों को परिभाषित करते हैं जिसमें हम अंतरिक्ष में वस्तु के अभिविन्यास और स्थिति पर विचार करेंगे। यह द्विभुज (ओरिएंटेशन क्वाटर्नेशन) के वास्तविक हिस्से को निर्दिष्ट करने के लिए किया जाना चाहिए, रोटेशन क्रम जिसमें अभिविन्यास कोणों से परिणामी चतुर्धातुकता को प्रभावित करता है। यहाँ हम हवाई जहाज के कोणों द्वारा निर्देशित होंगे - जम् $$$\ psi$ , पिच $$$\ _ वर्तते$ और रोल करें $$$गामा$ ।

आधार समन्वय प्रणाली को परिभाषित करें। कल्पना कीजिए कि आप पृथ्वी की सतह पर खड़े हैं और उत्तर की दिशा में देख रहे हैं।

बिंदु O _o - समन्वय प्रणाली की उत्पत्ति, वस्तु की उत्पत्ति के बिंदु पर स्थित है।
धुरी O _o Y _g - उर्ध्वाधर ऊपर की ओर निर्देशित है, और गुरुत्वाकर्षण वेक्टर की दिशा के विपरीत है।
अक्ष O _o X _g - स्थानीय मेरिडियन के स्पर्शरेखा के साथ उत्तर की ओर निर्देशित है।
एक्सिस ओ _ओ जेड _जी - सिस्टम को दाईं ओर पूरक करता है और पूर्व की ओर दाईं ओर निर्देशित किया जाता है।

दूसरा समन्वय प्रणाली जुड़ा हुआ है। उदाहरण के लिए, एक हवाई जहाज या अन्य वस्तु की कल्पना करें।
बिंदु ओ - एक नियम के रूप में, समन्वय प्रणाली की उत्पत्ति, वस्तु के द्रव्यमान के केंद्र के बिंदु पर स्थित है।
ओए अक्ष - वस्तु के क्षैतिज तल पर लंबवत ऊपर की ओर और लंबवत निर्देशित।
एक्सिस ओएक्स - वस्तु के सामने बिंदु के लिए आगे निर्देशित।
ओजेड अक्ष - सिस्टम को दाईं ओर पूरक करता है।

अंतरिक्ष में वस्तु की स्थिति निर्धारित आधार समन्वय प्रणाली के सापेक्ष संबद्ध समन्वय प्रणाली की उत्पत्ति (बिंदु O ) की त्रिज्या वेक्टर द्वारा निर्धारित की जाती है। आधार के सापेक्ष संबंधित समन्वय प्रणाली का उन्मुखीकरण तीन क्रमिक परिवर्तनों द्वारा निर्धारित किया जाता है:

यव कोण $$$\ psi$ - अक्ष के चारों ओर घूर्णन ओए ,
पिच कोण $$$\ _ वर्तते$ - धुरी OZ के चारों ओर रोटेशन,
रोल कोण $$$गामा$ - अक्ष OX के चारों ओर घूमना।

बाइकरनेशन के प्रारंभिक निर्धारण के लिए, आपको बाइकेटरियन के वास्तविक और दोहरे भागों को निर्दिष्ट करना होगा। ऑब्जेक्ट का अभिविन्यास और स्थिति अभिविन्यास कोणों का उपयोग करके एक निश्चित आधार समन्वय प्रणाली के सापेक्ष सेट किया गया है $$$\ psi, \ vartheta, \ gamma$ और द्रव्यमान के केंद्र की स्थिति वेक्टर $$$r = (r_x, r_y, r_z) ^ T$ ।

असली हिस्सा $$$\ textbf {q} _1$ सूत्र का उपयोग करके सेट किया जा सकता है:

$$

$$\ textbf {q} _1 = \ start {bmatrix} \ cos \ frac {\ psi} {2} \ cos \ frac {\ _ vartheta} {2} \ cos \ frac {\ _ \ _ गामा} [2} & - & \ _ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} / cos \ frac { \ vartheta} {2} \ sin \ frac {\ gamma} {2} और + और \ sin \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ cos \ frac {\ _ gma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ vartheta} {2} \ sin \ frac {\ _ गामा} {2} & + \ _ \ _ पाप \ _ \ _} {psi} { 2} \ cos \ frac {\ vartheta} {2} \ cos \ frac {\ gamma} {2} \\ \ cos \ frac {\ psi} {2} \ sin \ frac {\ _ vartheta {2} \ cos \ frac {\ gamma} {2} & - & \ sin \ frac {\ _ psi} {2} \ cos \ frac {\ vartheta} {2} \ sin \ frac {\ gamma} {2} अंत {bmatrix}$$

कृपया ध्यान दें कि यदि आपके पास एक अलग रोटेशन अनुक्रम है, तो अभिव्यक्तियां भी अलग होंगी।

दोहरा हिस्सा $$$\ textbf {q} _2$ अभिव्यक्ति द्वारा परिभाषित:

$$

$$\ textbf {q} _2 = \ frac12 \ textbf {r} \ otimes \ textbf {q} _1$$

अभिविन्यास कोणों की गणना और द्विआधारी से स्थिति वेक्टर। उलटा परिवर्तन

अभिविन्यास के कोणों की गणना जीवमंडल के वास्तविक भाग से की जा सकती है $$$\ textbf {q} _1$ :

$$

$$\ psi = \ arctan {\ frac {2 (q_0 q_2 - q_1 q_3)} {q_0 ^ 2 + q_1 ^ 2 - q_2 ^ 2 - q_3 ^ 2}}$$

$$

$$\ vartheta = \ arcsin {(2 (q_1 q_2 + q_0 q_3)) 2$$

$$

$$\ Gamma = \ arctan {\ frac {2 (q_0 q_1 - q_2 q_3)} {q_0 ^ 2 - q_1 ^ 2 + q_2 ^ 2 - q_3 ^ 2}}$$

ऑब्जेक्ट की स्थिति अभिव्यक्ति द्वारा निर्धारित की जाती है:

$$

$$\ textbf {r} = 2 \ textbf {q} _2 \ otimes \ textbf {q} _1 ^ {- 1}$$

परिणाम चतुर्धातुक रूप में एक वेक्टर है $$$\ textbf {r} = (0, r_x, r_y, r_z) ^ $$

सदिश द्विअर्थी घुमाएँ और घुमाएँ

द्विबीजपत्री के महान गुणों में से एक वेक्टर और एक समन्वय प्रणाली से दूसरे में घुमाव और आंदोलन है। O _o X X _G Y _G Z एक निश्चित आधार समन्वय प्रणाली है, और OXYZ ऑब्जेक्ट का कनेक्टेड समन्वय प्रणाली है। तब आधार समन्वय प्रणाली के सापेक्ष वस्तु का अभिविन्यास और स्थिति द्विभुज द्वारा निर्दिष्ट किया जा सकता है $$$\ widetilde {\ textbf {q}}$ । यदि एक वेक्टर निर्दिष्ट है $$$\ textbf {r}$ एक जुड़े समन्वय प्रणाली में, फिर आप एक वेक्टर प्राप्त कर सकते हैं $$$\ textbf {r} _0$ सूत्र का उपयोग करते हुए आधार समन्वय प्रणाली में:

$$

$$\ textbf {r} _0 = \ widetilde {\ textbf {q}} \ otimes \ textbf {r} \ otimes \ widetilde {\ textbf {q}} ^ {- 1 -$$

और पीछे:

$$

$$\ textbf {r} = \ widetilde {\ textbf {q}} ^ {- 1} \ otimes \ textbf {r} _0 \ otimes \ widetilde {\ textbf {q}:$$

जहाँ $$$\ textbf {r}$ विचित्र रूप में एक वेक्टर है, $$$\ textbf {r} = (1, 0, 0, 0, 0, 0, r_x, r_y, r_z)$

Biquaternion जावास्क्रिप्ट लाइब्रेरी

सभी प्रकार के संचालन के साथ biquaternions को जावास्क्रिप्ट-लाइब्रेरी में कार्यान्वित किया जाता है, आपके कार्यों के आधार पर, इसे अन्य प्रोग्रामिंग भाषाओं में लागू किया जा सकता है। जीविका के साथ काम करने के मुख्य कार्य:

समारोह	विवरण
DualQuaternion.dq	8 नंबर की एक सरणी के रूप में Biquaternion शरीर
DualQuaternion(dq0, dq1, dq2, dq3, dq4, dq5, dq6, dq7)	एक कंस्ट्रक्टर जो सभी आठ नंबरों को निर्दिष्ट करके एक biquaternion को परिभाषित करता है
DualQuaternion.fromEulerVector(psi, theta, gamma, v)	यूलर एंगल्स के साथ ऑब्जेक्ट के ओरिएंटेशन और ऑब्जेक्ट के पोजीशन वेक्टर को सेट करके बाइकेटरनियन प्राप्त करें
DualQuaternion.getEulerVector()	ईयूलर एंगल और पोज़िशन वेक्टर को बाइकेटरियन से प्राप्त करें
DualQuaternion.getVector()	बाइकरनेशन से स्थिति वेक्टर प्राप्त करें
DualQuaternion.getReal()	बाइकेटरियन का वास्तविक भाग प्राप्त करें (अंतरिक्ष में वस्तु के उन्मुखीकरण को निर्धारित करता है)
DualQuaternion.getDual()	द्विविभाजन का दोहरा भाग प्राप्त करें (अंतरिक्ष में वस्तु की स्थिति निर्धारित करता है)
DualQuaternion.norm()	द्विअर्थी मानदंड को एक दोहरी संख्या के रूप में प्राप्त करें
DualQuaternion.mod()	द्विअर्थी मॉड्यूल को दोहरी संख्या के रूप में प्राप्त करें
DualQuaternion.conjugate()	संयुग्मित द्विविभाजन प्राप्त करें
DualQuaternion.inverse()	उल्टा Biquaternion प्राप्त करें
DualQuaternion.mul(DQ2)	द्विबीजपत्री गुणन
DualQuaternion.toString()	उदाहरण के लिए, डिबग कंसोल के आउटपुट के लिए बाइकरनेटियन को स्ट्रिंग में बदलें

द्विविवाह के साथ काम करने का एक उदाहरण

एक उदाहरण के रूप में biquaternions का उपयोग करने की मूल बातें की बेहतर समझ के लिए, एक छोटे खेल पर विचार करें। आयताकार क्षेत्र सेट है - नक्शा। नक्शे पर तैरने वाली रोटरी बंदूक के साथ एक जहाज तैर रहा है। यहां यह ध्यान रखना आवश्यक है कि जहाज के लिए बुनियादी समन्वय प्रणाली नक्शे की समन्वय प्रणाली है, और बंदूक के लिए बुनियादी समन्वय प्रणाली जहाज है। सभी ऑब्जेक्ट मैप कोऑर्डिनेट सिस्टम में खींचे जाते हैं और यहाँ यह देखना दिलचस्प होगा कि आप कैसे बैकुंठ गुणन संपत्ति का उपयोग करके गन कोऑर्डिनेट सिस्टम से मैप कोऑर्डिनेट सिस्टम में जा सकते हैं। जहाज की चाल को डब्ल्यू, ए, एस, डी द्वारा नियंत्रित किया जाता है। बंदूक की दिशा माउस कर्सर द्वारा निर्धारित की जाती है।



जहाज और बंदूक दो वर्गों द्वारा वर्णित हैं: Ship और Gun । शिप क्लास के कंस्ट्रक्टर में, बाइकेटरनियन पॉइंट के रूप में इसका आकार, इस. this.dq_pos के रूप में मैप पर प्रारंभिक ओरिएंटेशन और स्थिति this.dq_pos ।

जहाज नियंत्रण के लिए द्विअर्थी वेतन वृद्धि भी दी जाती है। जब आगे और पीछे की (कीज़ W, S) चलती है, तो केवल द्विभुज का दोहरा भाग बदल जाएगा, और जब बाएं और दाएं (कुंजियाँ A, D) को नियंत्रित किया जाएगा, तो द्विभुज का वास्तविक और दोहरा हिस्सा बदल जाएगा, जो घूर्णन कोण सेट करता है।

 function Ship(ctx, v) { this.ctx = ctx; this.dq_pos = new DualQuaternion.fromEulerVector(0*Math.PI/180, 0, 0, v); //   this.dq_forward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, -10]); this.dq_forward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [ 15, 0, 10]); this.dq_backward_left = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, -10]); this.dq_backward_right = new DualQuaternion.fromEulerVector(0, 0, 0, [-15, 0, 10]); this.dq_forward_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 30, 0, 0]); //      this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 1, 0, 0]); this.dq_dx_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [-1, 0, 0]); return this; }; 

कक्षा में ही, Ship.draw() जहाज को प्रस्तुत करने का केवल एक कार्य है। जहाज के प्रत्येक बिंदु को वर्तमान स्थिति के biquaternion और जहाज के अभिविन्यास के साथ गुणा करने के biquaternion ऑपरेशन के आवेदन पर ध्यान दें।

 Ship.prototype = { 'ctx': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, 0, 0, 0), /** *   */ 'draw': function() { //         v_pos = this.dq_pos.getVector(); v_forward_left = this.dq_pos.mul(this.dq_forward_left).getVector(); v_forward_right = this.dq_pos.mul(this.dq_forward_right).getVector(); v_backward_left = this.dq_pos.mul(this.dq_backward_left).getVector(); v_backward_right = this.dq_pos.mul(this.dq_backward_right).getVector(); v_forward_forward = this.dq_pos.mul(this.dq_forward_forward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward_left[0], v_backward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_left[0], v_forward_left[2]); ctx.lineTo(v_forward_forward[0], v_forward_forward[2]); ctx.lineTo(v_forward_right[0], v_forward_right[2]); ctx.lineTo(v_backward_right[0], v_backward_right[2]); ctx.lineTo(v_backward_left[0], v_backward_left[2]); ctx.stroke(); ctx.closePath(); } }; 

गन क्लास के कंस्ट्रक्टर में, बाइकेटरनियन पॉइंट के रूप में इसका आकार निर्दिष्ट है। बंदूक को एक लाइन के रूप में प्रदर्शित किया जाएगा। जहाज पर प्रारंभिक अभिविन्यास और स्थिति इस. this.dq_pos द्वारा निर्धारित की गई है। इसके अलावा, जिस जहाज पर यह स्थापित किया गया है, उसके लिए बाध्यकारी भी सेट है। जहाज पर लगी बंदूक केवल घूम सकती है, इसलिए बंदूक को नियंत्रित करते समय द्विभाजित वेतन वृद्धि केवल बाइकेटरनियन के वास्तविक हिस्से को बदल देगी, जो रोटेशन के कोण को निर्धारित करता है। इस उदाहरण में, कार्यान्वयन माउस कर्सर द्वारा निर्देशित है, इसलिए बंदूक का रोटेशन तुरन्त होगा।

 function Gun(ctx, ship, v) { this.ctx = ctx; this.ship = ship; //     this.dq_pos = new DualQuaternion.fromEulerVector(0, 0, 0, v); //   this.dq_forward = new DualQuaternion.fromEulerVector(0, 0, 0, [20, 0, 0]); this.dq_backward = new DualQuaternion.fromEulerVector(0, 0, 0, [ 0, 0, 0]); //     this.dq_dx_left = new DualQuaternion.fromEulerVector( 1*Math.PI/180, 0, 0, [0, 0, 0]); this.dq_dx_right = new DualQuaternion.fromEulerVector(-1*Math.PI/180, 0, 0, [0, 0, 0]); return this; }; 

बंदूक वर्ग में, इसके प्रतिपादन का केवल एक कार्य Ship.draw() भी लागू किया जाता है। बंदूक को एक लाइन के रूप में प्रदर्शित किया जाता है, जिसे दो बिंदुओं द्वारा सेट किया जाता है this.dq_backward और this.dq_forward । बंदूक के बिंदुओं के निर्देशांक को निर्धारित करने के लिए, द्विबीजपत्री गुणन के संचालन का उपयोग किया जाता है।

 Gun.prototype = { 'ctx': 0, 'ship': 0, 'dq_pos': new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]), /** *   */ 'draw': function() { //     v_pos = this.ship.dq_pos.getVector(); v_forward = this.ship.dq_pos.mul(this.dq_backward).mul(this.dq_forward).getVector(); v_backward = this.ship.dq_pos.mul(this.dq_backward).getVector(); //   ctx.beginPath(); ctx.moveTo(v_backward[0], v_backward[2]); ctx.lineTo(v_forward[0], v_forward[2]); ctx.stroke(); ctx.closePath(); } }; 

घटनाओं के माध्यम से जहाज और बंदूक नियंत्रण प्रसंस्करण लागू किया जाता है। चार चर leftPressed, upPressed, rightPressed, downPressed , जो मुख्य प्रोग्राम लूप में संसाधित होते हैं, जहाज नियंत्रण कुंजी को दबाने और जारी करने के लिए जिम्मेदार होते हैं।

 leftPressed = false; rightPressed = false; upPressed = false; downPressed = false; dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [0, 0, 0]); document.addEventListener("keydown", keyDownHandler, false); document.addEventListener("keyup", keyUpHandler, false); document.addEventListener("mousemove", mouseMoveHandler, false); //     function keyDownHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = true; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = true; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = true; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = true; } //  S } //     function keyUpHandler(e) { if (e.keyCode == 37 || e.keyCode == 65 || e.keyCode == 97) { leftPressed = false; } //  A else if (e.keyCode == 38 || e.keyCode == 87 || e.keyCode == 119) { upPressed = false; } //  W else if (e.keyCode == 39 || e.keyCode == 68 || e.keyCode == 100) { rightPressed = false; } //  D else if (e.keyCode == 40 || e.keyCode == 83 || e.keyCode == 115) { downPressed = false; } //  S } 

सबसे दिलचस्प कार्यों में से एक, बाइकेटरनियन संचालन का उपयोग करने के दृष्टिकोण से, माउस पॉइंटर की दिशा में जहाज की बंदूक को नियंत्रित करना है। सबसे पहले, माउस पॉइंटर के निर्देशांक dq_mouse_pos में निर्धारित किए जाते हैं। फिर, जहाज के सापेक्ष माउस की स्थिति के द्विभाजक की गणना द्विभाजन गुणन का उपयोग करके की जाती है। जहाज का dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); माउस dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos);
(नोट: अनुक्रमिक द्विबीजपत्री गुणन संचालनों को दाएं से बाएं पढ़ा गया)। और अंत में, उपकरण और माउस के वैक्टर के बीच का कोण निर्धारित किया जाता है। बंदूक का प्रारंभिक बिंदु gun_1.dq_backward प्राप्त मान को सौंपा गया है।

 function mouseMoveHandler(e) { var relativeX = e.clientX - canvas.offsetLeft; var relativeY = e.clientY - canvas.offsetTop; //           if (relativeX > 0 && relativeX < canvas.width && relativeY > 0 && relativeY < canvas.height) { //    dq_mouse_pos = new DualQuaternion.fromEulerVector(0, 0, 0, [relativeX, 0, relativeY]); //      //  .       //     // DQ_ship^(-1) * DQ_mouse dq_mouse_pos_about_ship = ship_1.dq_pos.inverse().mul(dq_mouse_pos); //       q_gun_mouse = new Quaternion.fromBetweenVectors(gun_1.dq_forward.getVector(), dq_mouse_pos_about_ship.getVector()); dq_gun_mouse = new DualQuaternion(q_gun_mouse.q[0], q_gun_mouse.q[1], q_gun_mouse.q[2], q_gun_mouse.q[3], 0, 0, 0, 0); gun_1.dq_backward = dq_gun_mouse; // console.log(dq_gun_mouse.getEulerVector()); // console.log(relativeX + ' ' + relativeY + ' ' + gun_1.dq_forward.toString()); } } 

कार्यक्रम के मुख्य निकाय में, जहाज और बंदूकें ship_1 और gun_1 , डिबगिंग जानकारी प्रदर्शित की जाती है और जहाज नियंत्रण प्रसंस्करण किया जाता है।

 var canvas = document.getElementById("myCanvas"); var ctx = canvas.getContext("2d"); ship_1 = new Ship(ctx, [100, 0, 100]); gun_1 = new Gun(ctx, ship_1, [0, 0, 0]); function draw() { ctx.clearRect(0, 0, canvas.width, canvas.height); ship_1.draw(); gun_1.draw(); // Debug info ship_euler_vector = ship_1.dq_pos.getEulerVector(); ship_euler_vector[0] = ship_euler_vector[0]*180/Math.PI; ship_euler_vector[1] = ship_euler_vector[1]*180/Math.PI; ship_euler_vector[2] = ship_euler_vector[2]*180/Math.PI; ship_euler_vector = ship_euler_vector.map(function(each_element){ return each_element.toFixed(2); }); ship_dq = ship_1.dq_pos.dq.map(function(each_element){ return each_element.toFixed(2); }); gun_dq = ship_1.dq_pos.mul(gun_1.dq_backward).dq.map(function(each_element){ return each_element.toFixed(2); }); ctx.font = "8pt Courier"; ctx.fillText("Ship: " + ship_dq + " | psi, theta, gamma, vector:" + ship_euler_vector, 10, 20); ctx.fillText("Gun: " + gun_dq, 10, 40); //   if (leftPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_left); } if (rightPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_right); } if (upPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_forward); } if (downPressed) { ship_1.dq_pos = ship_1.dq_pos.mul(ship_1.dq_dx_backward); } requestAnimationFrame(draw); } draw(); 

संग्रह के लिंक में quaternions और biquaternions, प्रोग्राम स्क्रिप्ट ही और index.html फ़ाइल के साथ काम करने के लिए पुस्तकालयों का पूरा कोड है, जो उपरोक्त उदाहरण को चलाने के लिए ब्राउज़र में स्थानीय रूप से खोला जा सकता है।

द्विविवाह के साथ काम करने का एक उदाहरण

निष्कर्ष

आपके पास एक प्रश्न हो सकता है: जब आप वस्तुओं को हिलाने और घुमाने के लिए मानक उपकरणों के साथ प्राप्त कर सकते हैं तो ऐसे जटिल गणितीय तंत्र का उपयोग क्यों करें? मुख्य लाभों में से एक यह है कि लेखन का द्विभाजित रूप अधिक कम्प्यूटेशनल रूप से कुशल है, क्योंकि भावों के विस्तारित होने के बाद के विभाजनों के साथ सभी संचालन रैखिक होते हैं। यह वीडियो, जियोमेट्रिक स्किनिंग विथ एप्रोक्सिमेट ड्यूल क्वाटर्नियन ब्लेंडिंग, दिखाता है कि अन्य तरीकों की तुलना में कितना अधिक कुशल है द्विभाजन गणना।

मैंने मुख्य रूप से अंग्रेजी स्रोतों से biquaternions के उपयोग के बारे में जानकारी ली।
घरेलू साहित्य से, मैं दो पुस्तकों की सलाह दे सकता हूं:

1. चेलनोकोव यूरी निकोलाइविच। चतुर्धातुक और द्विवार्षिक मॉडल और ठोस यांत्रिकी के तरीके और उनके अनुप्रयोग। गति की ज्यामिति और कीनेमेटीक्स। - स्मारकीय सैद्धांतिक कार्य।
2. गोर्डीव वादिम निकोलाइविच। ज्यामिति और यांत्रिकी में आवेदन के साथ चतुर्धातुक और द्विवचन। - यह एक अधिक समझने योग्य भाषा में लिखा गया है और घुमावदार स्थानिक संरचनाओं को आकार देने के कार्यों में अनुप्रयोगों को दर्शाता है।