💵 ✂️ 💇🏼 पुनरावृत्ति और पुरस्कार जोड़कर स्टॉक-आधारित क्यू-लर्निंग एजेंट में सुधार 🔷 🚝 🌤️

अनुस्मारक

नमस्कार, हेब्र! मैं आपके नए लेख का एक और अनुवाद माध्यम से आपके ध्यान में लाता हूं।

पिछली बार ( पहला लेख ) ( हैबर ), हमने क्यू-लर्निंग तकनीक का उपयोग करके एक एजेंट बनाया, जो नकली और वास्तविक विनिमय समय श्रृंखला पर लेनदेन करता है और यह जांचने की कोशिश करता है कि कार्यों का यह क्षेत्र प्रबलित सीखने के लिए उपयुक्त है या नहीं।

इस बार हम प्रक्षेपवक्र के भीतर खाते की निर्भरता को ध्यान में रखते हुए एक LSTM परत जोड़ेंगे और प्रस्तुतियों के आधार पर इंजीनियरिंग को पुरस्कृत करेंगे।

मैं आपको याद दिला दूं कि अवधारणा को सत्यापित करने के लिए, हमने निम्नलिखित सिंथेटिक डेटा का उपयोग किया:

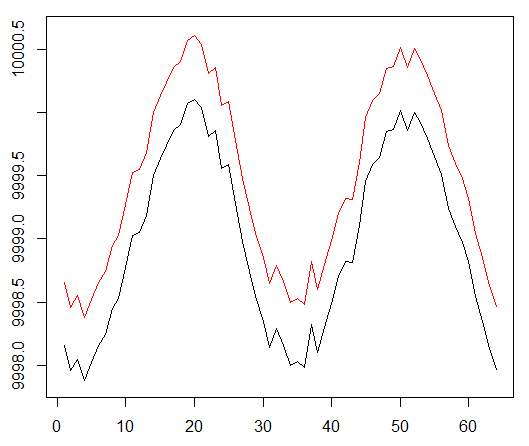
सिंथेटिक डेटा: सफेद शोर के साथ साइन।

साइन फ़ंक्शन पहला प्रारंभिक बिंदु था। दो वक्र एक परिसंपत्ति की खरीद और बिक्री मूल्य का अनुकरण करते हैं, जहां प्रसार न्यूनतम लेनदेन लागत है।

हालाँकि, इस बार हम इस सरल कार्य को क्रेडिट असाइनमेंट पथ का विस्तार करते हुए जटिल बनाना चाहते हैं:

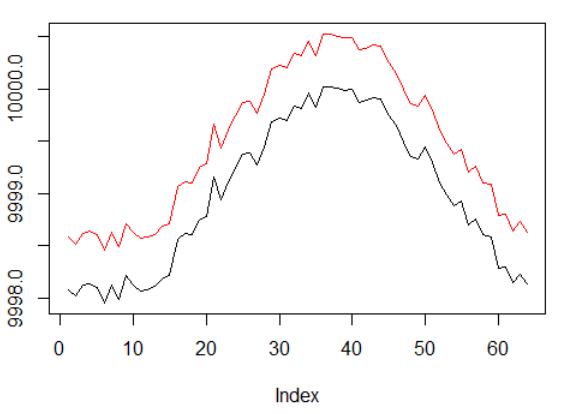
सिंथेटिक डेटा: सफेद शोर के साथ साइन।

साइनस चरण दोगुना हो गया था।

इसका मतलब यह है कि विरल पुरस्कार जो हम उपयोग करते हैं, वे लंबे समय तक प्रक्षेपवक्र में फैलने चाहिए। इसके अलावा, हम एक सकारात्मक इनाम प्राप्त करने की संभावना को काफी कम कर देते हैं, क्योंकि एजेंट को लेनदेन की लागतों को दूर करने के लिए 2 बार लंबे समय तक सही क्रियाओं का क्रम करना पड़ता था। दोनों कारक आरआईएल के लिए भी कार्य को जटिल करते हैं यहां तक कि एक साधारण लहर के रूप में ऐसी सरल परिस्थितियों में भी।

इसके अलावा, हमें याद है कि हमने इस तंत्रिका नेटवर्क वास्तुकला का उपयोग किया था:

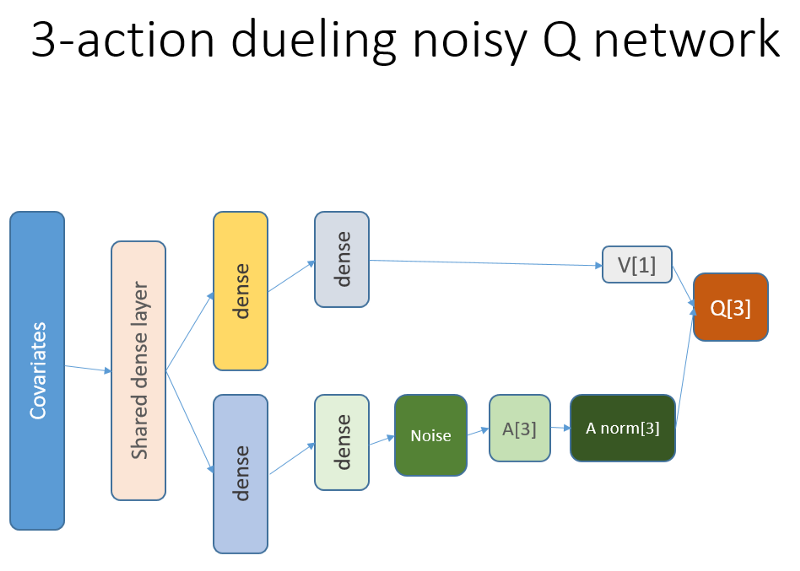
क्या जोड़ा गया और क्यों

LSTM

सबसे पहले, हम एजेंट को प्रक्षेपवक्र के भीतर परिवर्तनों की गतिशीलता की अधिक समझ देना चाहते थे। सीधे शब्दों में, एजेंट को अपने स्वयं के व्यवहार को बेहतर ढंग से समझना चाहिए: उसने अभी और पिछले कुछ समय से क्या किया, और राज्य-कार्यों के वितरण के साथ-साथ प्राप्त पुरस्कारों को कैसे विकसित किया। पुनरावृत्ति परत का उपयोग करके इस समस्या को ठीक से हल किया जा सकता है। प्रयोग के एक नए सेट को लॉन्च करने के लिए इस्तेमाल किए गए नए आर्किटेक्चर में आपका स्वागत है:

कृपया ध्यान दें कि मैंने विवरण में थोड़ा सुधार किया है। पुराने एनएन से एकमात्र अंतर पूरी तरह से बंधुआ के बजाय पहले छिपी हुई एलएसटीएम परत है।

कृपया ध्यान दें कि काम में LSTM के साथ, हमें प्रशिक्षण के लिए अनुभव के प्रजनन के उदाहरणों के चयन को बदलना होगा: अब हमें अलग-अलग उदाहरणों के बजाय संक्रमण अनुक्रमों की आवश्यकता है। यहां बताया गया है कि यह कैसे काम करता है (यह एल्गोरिदम में से एक है)। हमने पहले नमूने का उपयोग किया था:

प्लेबैक बफर की काल्पनिक योजना।

हम LSTM के साथ इस योजना का उपयोग करते हैं:

अब अनुक्रम चुने गए हैं (जिनकी लंबाई हम आनुभविक रूप से निर्दिष्ट करते हैं)।

पहले की तरह, और अब टेम्पोरल-टेम्पोरल लर्निंग की त्रुटियों के आधार पर नमूना को एक प्राथमिकता एल्गोरिथ्म द्वारा विनियमित किया जाता है।

LSTM पुनरावृत्ति स्तर अतीत के अंतराल में छिपे एक अतिरिक्त सिग्नल को रोकने के लिए समय श्रृंखला से सूचना के सीधे प्रसार की अनुमति देता है। हमारे साथ समय श्रृंखला आकार के साथ एक दो आयामी टेंसर है: हमारे राज्य-कार्रवाई के प्रतिनिधित्व पर अनुक्रम की लंबाई।

प्रस्तुतियों

क्षमता के आधार पर पुरस्कार विजेता इंजीनियरिंग, पोटेंशियल बेस्ड रिवार्ड शेपिंग (PBRS) एक शक्तिशाली उपकरण है जो आपको हमारे पर्यावरण को हल करने के लिए नीति खोज प्रक्रिया की अनुकूलता की गति, स्थिरता को बढ़ाने और उल्लंघन न करने की अनुमति देता है। मैं इस विषय पर कम से कम इस मूल दस्तावेज को पढ़ने की सलाह देता हूं:

people.eecs.berkeley.edu/~russell/papers/ml99-shaping.ps

संभावित यह निर्धारित करता है कि हमारा वर्तमान राज्य लक्ष्य राज्य के सापेक्ष कितना अच्छा है जिसे हम दर्ज करना चाहते हैं। यह कैसे काम करता है इसका एक योजनाबद्ध दृष्टिकोण:

ऐसे विकल्प और कठिनाइयाँ हैं जिन्हें आप परीक्षण और त्रुटि के बाद समझ सकते हैं, और हम इन विवरणों को छोड़ देते हैं, जो आपको आपके होमवर्क के साथ छोड़ देते हैं।

यह एक और बात का उल्लेख करने योग्य है, जो यह है कि पीबीआरएस को प्रस्तुतियों का उपयोग करके उचित ठहराया जा सकता है, जो पर्यावरण में एजेंट के लगभग इष्टतम व्यवहार के बारे में विशेषज्ञ (या सिम्युलेटेड) ज्ञान का एक रूप है। अनुकूलन योजनाओं का उपयोग करके हमारे कार्य के लिए ऐसी प्रस्तुतियाँ खोजने का एक तरीका है। हम खोज के विवरण को छोड़ देते हैं।

संभावित इनाम निम्नलिखित रूप लेता है (समीकरण 1):

r '= r + गामा * F (s') - F (s)

जहां एफ राज्य की क्षमता है, और आर प्रारंभिक इनाम है, गामा छूट कारक है (0: 1)।

इन विचारों के साथ, हम कोडिंग की ओर बढ़ते हैं।

आर में कार्यान्वयन
यहाँ केर नेटवर्क API पर आधारित तंत्रिका नेटवर्क कोड है:

कोड

# configure critic NN — — — — — — library('keras') library('R6') state_names_length <- 12 # just for example lstm_seq_length <- 4 learning_rate <- 1e-3 a_CustomLayer <- R6::R6Class( “CustomLayer” , inherit = KerasLayer , public = list( call = function(x, mask = NULL) { x — k_mean(x, axis = 2, keepdims = T) } ) ) a_normalize_layer <- function(object) { create_layer(a_CustomLayer, object, list(name = 'a_normalize_layer')) } v_CustomLayer <- R6::R6Class( “CustomLayer” , inherit = KerasLayer , public = list( call = function(x, mask = NULL) { k_concatenate(list(x, x, x), axis = 2) } , compute_output_shape = function(input_shape) { output_shape = input_shape output_shape[[2]] <- input_shape[[2]] * 3L output_shape } ) ) v_normalize_layer <- function(object) { create_layer(v_CustomLayer, object, list(name = 'v_normalize_layer')) } noise_CustomLayer <- R6::R6Class( “CustomLayer” , inherit = KerasLayer , lock_objects = FALSE , public = list( initialize = function(output_dim) { self$output_dim <- output_dim } , build = function(input_shape) { self$input_dim <- input_shape[[2]] sqr_inputs <- self$input_dim ** (1/2) self$sigma_initializer <- initializer_constant(.5 / sqr_inputs) self$mu_initializer <- initializer_random_uniform(minval = (-1 / sqr_inputs), maxval = (1 / sqr_inputs)) self$mu_weight <- self$add_weight( name = 'mu_weight', shape = list(self$input_dim, self$output_dim), initializer = self$mu_initializer, trainable = TRUE ) self$sigma_weight <- self$add_weight( name = 'sigma_weight', shape = list(self$input_dim, self$output_dim), initializer = self$sigma_initializer, trainable = TRUE ) self$mu_bias <- self$add_weight( name = 'mu_bias', shape = list(self$output_dim), initializer = self$mu_initializer, trainable = TRUE ) self$sigma_bias <- self$add_weight( name = 'sigma_bias', shape = list(self$output_dim), initializer = self$sigma_initializer, trainable = TRUE ) } , call = function(x, mask = NULL) { #sample from noise distribution e_i = k_random_normal(shape = list(self$input_dim, self$output_dim)) e_j = k_random_normal(shape = list(self$output_dim)) #We use the factorized Gaussian noise variant from Section 3 of Fortunato et al. eW = k_sign(e_i) * (k_sqrt(k_abs(e_i))) * k_sign(e_j) * (k_sqrt(k_abs(e_j))) eB = k_sign(e_j) * (k_abs(e_j) ** (1/2)) #See section 3 of Fortunato et al. noise_injected_weights = k_dot(x, self$mu_weight + (self$sigma_weight * eW)) noise_injected_bias = self$mu_bias + (self$sigma_bias * eB) output = k_bias_add(noise_injected_weights, noise_injected_bias) output } , compute_output_shape = function(input_shape) { output_shape <- input_shape output_shape[[2]] <- self$output_dim output_shape } ) ) noise_add_layer <- function(object, output_dim) { create_layer( noise_CustomLayer , object , list( name = 'noise_add_layer' , output_dim = as.integer(output_dim) , trainable = T ) ) } critic_input <- layer_input( shape = list(NULL, as.integer(state_names_length)) , name = 'critic_input' ) common_lstm_layer <- layer_lstm( units = 20 , activation = “tanh” , recurrent_activation = “hard_sigmoid” , use_bias = T , return_sequences = F , stateful = F , name = 'lstm1' ) critic_layer_dense_v_1 <- layer_dense( units = 10 , activation = “tanh” ) critic_layer_dense_v_2 <- layer_dense( units = 5 , activation = “tanh” ) critic_layer_dense_v_3 <- layer_dense( units = 1 , name = 'critic_layer_dense_v_3' ) critic_layer_dense_a_1 <- layer_dense( units = 10 , activation = “tanh” ) # critic_layer_dense_a_2 <- layer_dense( # units = 5 # , activation = “tanh” # ) critic_layer_dense_a_3 <- layer_dense( units = length(actions) , name = 'critic_layer_dense_a_3' ) critic_model_v <- critic_input %>% common_lstm_layer %>% critic_layer_dense_v_1 %>% critic_layer_dense_v_2 %>% critic_layer_dense_v_3 %>% v_normalize_layer critic_model_a <- critic_input %>% common_lstm_layer %>% critic_layer_dense_a_1 %>% #critic_layer_dense_a_2 %>% noise_add_layer(output_dim = 5) %>% critic_layer_dense_a_3 %>% a_normalize_layer critic_output <- layer_add( list( critic_model_v , critic_model_a ) , name = 'critic_output' ) critic_model_1 <- keras_model( inputs = critic_input , outputs = critic_output ) critic_optimizer = optimizer_adam(lr = learning_rate) keras::compile( critic_model_1 , optimizer = critic_optimizer , loss = 'mse' , metrics = 'mse' ) train.x <- array_reshape(rnorm(10 * lstm_seq_length * state_names_length) , dim = c(10, lstm_seq_length, state_names_length) , order = 'C') predict(critic_model_1, train.x) layer_name <- 'noise_add_layer' intermediate_layer_model <- keras_model(inputs = critic_model_1$input, outputs = get_layer(critic_model_1, layer_name)$output) predict(intermediate_layer_model, train.x)[1,] critic_model_2 <- critic_model_1

अपनी अंतरात्मा की आवाज पर अपना फैसला ...

परिणाम और तुलना

चलो अंत परिणामों में सही गोता लगाएँ। नोट: सभी परिणाम बिंदु अनुमान हैं और विभिन्न रैंडम सीड्स के साथ कई रन पर भिन्न हो सकते हैं।

तुलना में शामिल हैं:

LSTM और प्रस्तुतियों के बिना पिछले संस्करण
सरल 2-तत्व LSTM
4-तत्व एलएसटीएम
पीबीआरएस पुरस्कार के साथ 4-सेल एलएसटीएम उत्पन्न

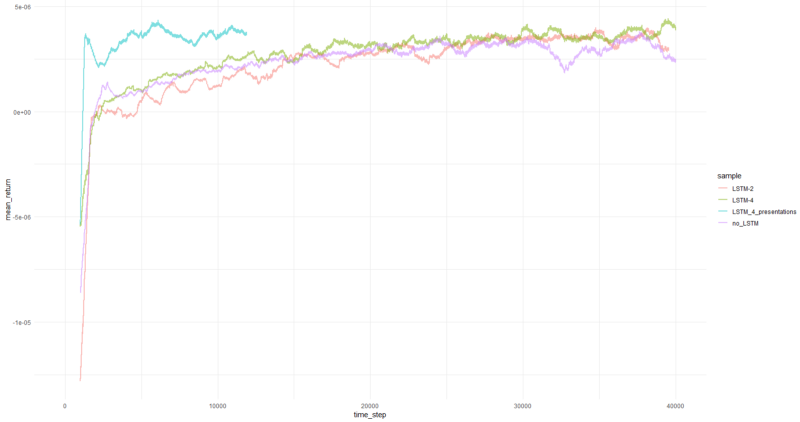
1000 एपिसोड से अधिक औसत प्रति एपिसोड औसत रिटर्न।

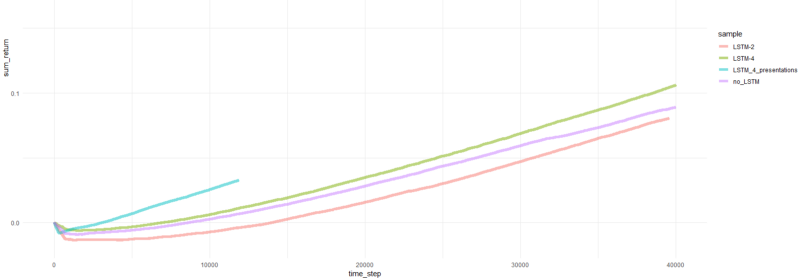
कुल एपिसोड की वापसी।

सबसे सफल एजेंट के लिए चार्ट:

एजेंट प्रदर्शन।

ठीक है, यह स्पष्ट है कि पीबीआरएस के रूप में एजेंट पहले के प्रयासों की तुलना में इतनी जल्दी और दृढ़ता से जुटता है कि इसे एक महत्वपूर्ण परिणाम के रूप में स्वीकार किया जा सकता है। प्रस्तुतियों के बिना गति लगभग 4-5 गुना अधिक है। स्थिरता अद्भुत है।

जब LSTM का उपयोग करने की बात आती है, तो 4 कोशिकाओं ने 2 कोशिकाओं से बेहतर प्रदर्शन किया। एक 2-सेल LSTM ने एक गैर-LSTM संस्करण की तुलना में बेहतर प्रदर्शन किया (हालांकि, शायद यह एक एकल प्रयोग का भ्रम है)।

अंतिम शब्द

हमने देखा है कि पुनरावृत्ति और क्षमता-निर्माण पुरस्कार मदद करते हैं। मुझे विशेष रूप से पसंद आया कि पीबीआरएस ने इतना उच्च प्रदर्शन कैसे किया।

किसी पर विश्वास न करें जो मुझे यह कहता है कि एक आरएल एजेंट बनाना आसान है जो अच्छी तरह से परिवर्तित होता है, क्योंकि यह एक झूठ है। सिस्टम में जोड़ा गया प्रत्येक नया घटक संभावित रूप से इसे कम स्थिर बनाता है और इसके लिए बहुत सारे कॉन्फ़िगरेशन और डीबगिंग की आवश्यकता होती है।

फिर भी, इस बात के स्पष्ट प्रमाण हैं कि समस्या का समाधान केवल इस्तेमाल किए गए तरीकों (डेटा बरकरार रहा) में सुधार करके किया जा सकता है। यह एक तथ्य है कि किसी भी कार्य के लिए मापदंडों की एक निश्चित सीमा दूसरों की तुलना में बेहतर काम करती है। इसे ध्यान में रखते हुए, आप एक सफल शिक्षण मार्ग पर चल रहे हैं।

आपका धन्यवाद