💗 👸🏿 📩 खरोंच से हेक्सापोड विकसित करना (भाग 3)

सभी को नमस्कार! हेक्सापॉड का विकास आगे बढ़ रहा है और अंत में बुनियादी गणितीय भाग का परीक्षण किया गया है और प्रलेखन के लिए तैयार है। परियोजना के अंत तक जीवित रहने और शेल्फ पर धूल इकट्ठा न करने के लिए, आपको इसकी सकारात्मक बदलाव देखने की जरूरत है, भले ही वे महत्वहीन हों। इस अनुच्छेद में, मैं उलटा किनेमैटिक्स समस्या को हल करने के लिए एक एल्गोरिथ्म के बारे में बात करूंगा और इसे कार्रवाई में प्रदर्शित करूंगा। मुझे उम्मीद है कि यह दिलचस्प होगा।

विकास के चरण:
भाग 1 - डिज़ाइन
भाग 2 - विधानसभा
भाग 3 - किनेमैटिक्स
भाग 4 - गणित के विषय और क्रम
भाग 5 - इलेक्ट्रॉनिक्स
भाग 6 - 3 डी प्रिंटिंग के लिए संक्रमण
भाग 7 - नए आवास, अनुप्रयोग सॉफ्टवेयर और संचार प्रोटोकॉल

समन्वय प्रणाली

शुरू करने के लिए, रोबोट के समन्वय प्रणालियों को निर्धारित करना आवश्यक है - उनमें से तीन के रूप में कई हैं:

वास्तव में, वे एक-दूसरे से अलग नहीं हैं, लेकिन मामले के विभिन्न स्थानों में स्थित हैं और किसी न किसी कोण पर एक-दूसरे के सापेक्ष घुमाए जा सकते हैं। जब ऊपर से देखा जाता है, तो कुल्हाड़ियों का स्थान निम्नानुसार होगा (coxa_zero_rotate पैरामीटर थोड़ा बाद में वर्णित किया जाएगा):

जैसा कि आप शायद पहले से ही देखते हैं, बाईं और दाईं ओर समन्वित सिस्टम शरीर के केंद्र के सापेक्ष सममित रूप से स्थित हैं। ऐसा लग रहा था कि यह आसान होगा।

प्रत्येक बिंदु के निर्देशांक उस अंग के सापेक्ष निर्धारित किए जाते हैं जिसके लिए यह बिंदु अभिप्रेत है। यह दृष्टिकोण आपको विन्यास के साथ हस्तक्षेप किए बिना दर्द को कहीं भी स्थानांतरित करने की अनुमति देता है।

और इसलिए वे अंग के सापेक्ष स्थित हैं:

लक्ष्य बिंदु के निर्देशांक मुख्य समन्वित प्रणाली के सापेक्ष हैं। प्रारंभ में, मैं मामले के केंद्र के सापेक्ष निर्देशांक सेट करना चाहता था, लेकिन यह बहुत सुविधाजनक नहीं था और कई अतिरिक्त मापदंडों के भंडारण की आवश्यकता थी।

इसके बाद, संकेतन X *, X **, आदि। X ′, X replaced will द्वारा प्रतिस्थापित किया जाएगा।

उलटा गतिज समस्या का समाधान

चलो मेरे लिए सबसे कठिन और दिलचस्प क्षण के साथ शुरू करते हैं - किनेमैटिक्स। मैंने स्वयं एल्गोरिथ्म का आविष्कार किया, कभी-कभी एक त्रिकोण और त्रिकोणमितीय कार्यों के गुणों को देखकर। यांत्रिकी के साथ, यह मेरे लिए कठिन है, और त्रिकोणमिति के साथ यह और भी बदतर है, इसलिए शायद कहीं मैं कुछ को ध्यान में नहीं रख सकता, लेकिन यह एल्गोरिथ्म काम करता है (अंत में वीडियो)।

1. समस्या का विवरण

मान लें कि हमें निर्देशांक (150; -20; 100) के साथ बिंदु ए तक पहुंचने के लिए सामने दाहिने अंग की आवश्यकता है। यह भी ज्ञात है कि अंग को शरीर के सापेक्ष 45 डिग्री तक घुमाया जाता है (पैरामीटर coxa_zero_rotate):

निम्‍नलिखित में निम्‍न पैरामीटर हैं:

मुझे लगता है कि आपको यह वर्णन करने की आवश्यकता नहीं है कि इन मापदंडों का क्या मतलब है, नाम खुद के लिए बोलते हैं। आप केवल यह जोड़ सकते हैं कि ये सभी पैरामीटर केस के कॉन्फ़िगरेशन द्वारा निर्धारित किए जाते हैं, बाहर से और लचीलेपन के लिए संपादित करने की क्षमता के साथ फ्लैश मेमोरी में स्थायी और संग्रहीत होते हैं।

इसलिए आपको इसकी आवश्यकता है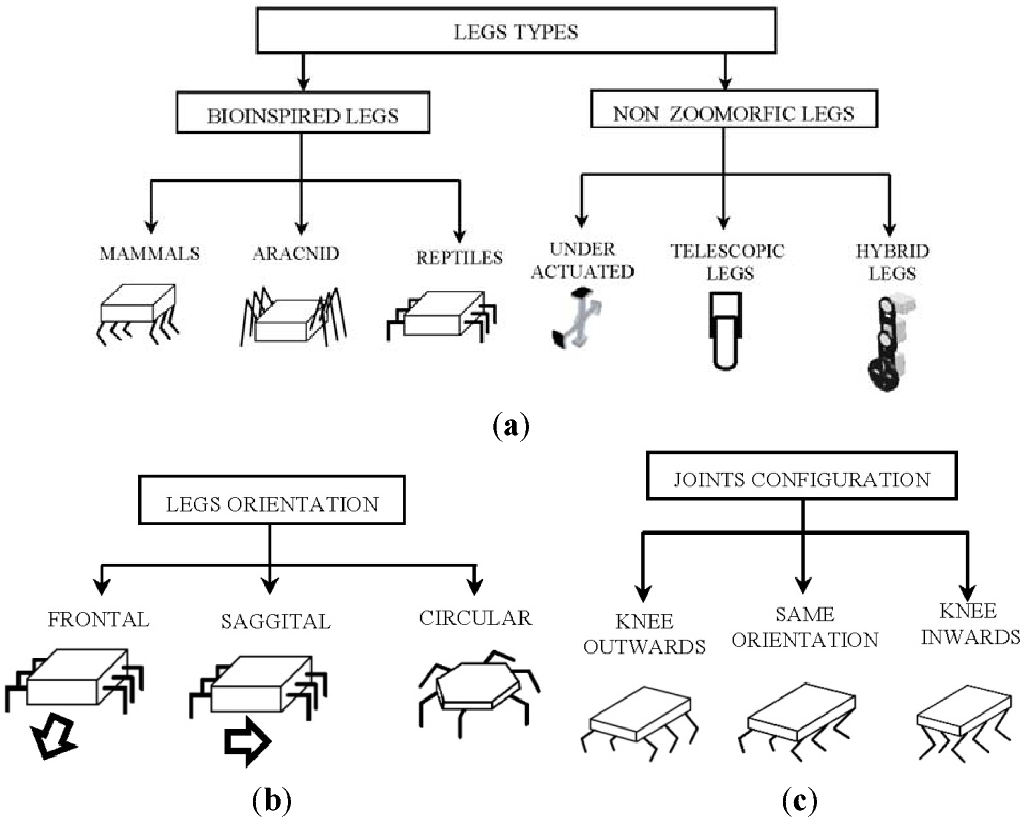

चित्र पतवार और हेक्सापॉड के पैरों के स्थान के विभिन्न रूपों को दर्शाता है। अब यह ARACNID कॉन्फ़िगरेशन से मेल खाता है। मान लीजिए कि मुझे मामले को REPTILES में बदलना पड़ा है, और इसके लिए यह केवल कार्यक्रम में माप के बिना मापदंडों के मूल्यों को बदलने के लिए पर्याप्त होगा, यहां तक कि लक्ष्य बिंदुओं को भी बदलना नहीं होगा (जब तक कि सही ढंग से यह दृष्टिकोण न हो)।

उपरोक्त सभी पैरामीटर समस्या को हल करने के लिए पर्याप्त हैं।

2. समस्या का समाधान

2.1 COXA के रोटेशन के कोण का पता लगाना

यह अवस्था सबसे सरल है। सबसे पहले आपको LIMB COORDINATE सिस्टम के सापेक्ष बिंदु A के निर्देशांक को पुनर्गणना करने की आवश्यकता है। जाहिर है, आपको कोण coxa_zero_rotate को घुमाने की जरूरत है, आप निम्न सूत्रों का उपयोग करके ऐसा कर सकते हैं:

$ $ प्रदर्शन $ $ x ′ = x कॉस (α) + z पाप (α) = १५० + कॉस (४५) + १०० (पाप (४५) = १8६. $ $ $ $ $ $ $ डिस्प्ले

$y ′ = y = -20$

$$ डिस्प्ले $$ z $ = -x sin (α) + z $ cos (α) = -150 -1 sin (45) + 100 (cos (45) = -35.36 $$ प्रदर्शन $$

इस प्रकार, हमें LIMB समन्वित प्रणाली के सापेक्ष लक्ष्य बिंदु A (176.78; -20; -35.36) के निर्देशांक मिले।

अब आप atan2 फ़ंक्शन का उपयोग करके COXA कोण पा सकते हैं:

$COXA = atan2 (z X, x =) = atan2 (-35.36, 176.78) = -11.30 °$

और इसलिए, हमें वह कोण मिला है जिसके द्वारा आपको COXA सर्वो को घुमाने की आवश्यकता है ताकि बिंदु A X weY ′ विमान में हो। आइए अब कोमपस 3 डी में हमारी गणना देखें:

बिलकुल ठीक।

2.2 FEMUR और TIBIA के रोटेशन के कोण का पता लगाना
इन कोणों को खोजने के लिए, X′Y these विमान पर जाना आवश्यक है। विमान पर जाने के लिए, आपको कोण COXA द्वारा उस बिंदु को घुमाना होगा, जिसकी हमने पहले ही गणना की थी।

$ $ प्रदर्शन $ $ x ′ = x display कॉस (α) + y ⋅ (पाप (α) = 176.78 (कॉस (-11) + -20 (पाप (-11) = 180.28 $ $ $ $ $

$y ′ = y = -20$

Y along का समन्वय नहीं बदलता, क्योंकि हम Y ′ अक्ष के साथ घूमते हैं।

अगला, आपको गणना से COXA की लंबाई को हटाने की आवश्यकता है, अर्थात। हम प्लेन X′′Y ′ के पास जाते हैं, इसके लिए हम COXA की लंबाई से बिंदु के निर्देशांक x of की एक शिफ्ट करते हैं:

$x x x = x ′ - coxaLength = 180.28 - 40 = 140.28$

$य ′ y = y ′$

इन सभी जोड़तोड़ों के बाद, समस्या का आगे का हल त्रिकोण के कोणों और बी को खोजने के लिए कम हो गया है:

कोणों को खोजने से पहले, आपको इस त्रिकोण के तीसरे पक्ष C को खोजने की आवश्यकता है। यह दूरी वेक्टर की लंबाई के अलावा और कुछ नहीं है और सूत्र द्वारा गणना की जाती है:

$ $ प्रदर्शन $ $ C = \ sqrt {x ′ + ^ 2 + y $ C ^ 2} = \ sqrt {140.28 ^ 2 + (-20) ^ 2} = 141.70 $ $ प्रदर्शन $ $

अब आपको यह जांचने की आवश्यकता है कि क्या अंग इस बिंदु तक पहुंच सकता है। यदि C, FEMUR और TIBIA की लंबाई के योग से अधिक है, तो बिंदु उपलब्ध नहीं है। हमारे मामले में, 141.70 <141 + 85 - बिंदु उपलब्ध है।

अब हम त्रिभुज के सभी पक्षों को जानते हैं और हम कोणों को खोज सकते हैं a और b जिसे हमें कॉशन प्रमेय का उपयोग करने की आवश्यकता है:

$a = acos ({A ^ 2 + C ^ 2 - B ^ 2 \ over 2AC}) = 72.05 °$

$b = acos ({B ^ 2 + A ^ 2 - C ^ 2 \ over 2BA}) = 72.95 °$

प्राप्त कोणों को उन्हें सर्वो में खिलाने के लिए लागू नहीं किया जाता है, क्योंकि प्रारंभिक स्थिति और सीधी रेखा C से X अक्ष तक झुकाव के कोण को यहां ध्यान नहीं दिया जाता है। यदि हम प्रारंभिक कोण FEMUR और TIBIA (135 ° और 45 °) को जानते हैं, तो झुकाव C का X अक्ष पर कोण नहीं है। यह सब जानते हैं। आप इसे फ़ंक्शन atan2 (y ′ x, x ′:) का उपयोग करके पा सकते हैं:

$ $ प्रदर्शन $ $ φ = atan2 (y ′ x, x ′ $) = atan2 (-20, 140.28) = -8.11 ° $ $ प्रदर्शन $ $

अंत में, आप FEMUR और TIBIA सर्वो के रोटेशन के कोण की गणना कर सकते हैं:

$FEMUR = femurZeroRotate - a - 135 = 135 - 72.05 + 8.11 = 71.06$

$FEMUR = b - tibiaZeroRotate = 45 - 72.95 = 27.95 °$

चलो हमारी गणना की जाँच करें:

यह सच जैसा लगता है।

परिणाम

गणना किए गए कोण COXA, FEMUR और TIBIA उनके सर्वो को खिलाने के लिए उपयुक्त हैं। आप देख सकते हैं कि COXA कोण नकारात्मक है और, तदनुसार, सवाल उठता है: "-11.3 डिग्री से ड्राइव को कैसे चालू करें?"। चाल यह है कि मैं एक तार्किक शून्य के रूप में सीओएक्सए सर्वो की तटस्थ स्थिति का उपयोग करता हूं, इससे ड्राइव सकारात्मक और नकारात्मक दोनों कोणों को घुमाने की अनुमति देता है। यह निश्चित रूप से स्पष्ट है, लेकिन मुझे लगता है कि यह उल्लेख करने के लिए जगह से बाहर नहीं होगा। मैं निम्नलिखित लेखों में इसके बारे में अधिक विस्तार से बात करूंगा जब मैं उपरोक्त सभी के कार्यान्वयन के बारे में बात करता हूं।

स्रोत कोड

पर्याप्त शब्द, मुझे कोड देखने दो

#define RAD_TO_DEG(rad) ((rad) * 180.0 / M_PI) #define DEG_TO_RAD(deg) ((deg) * M_PI / 180.0) typedef enum { LINK_COXA, LINK_FEMUR, LINK_TIBIA } link_id_t; typedef struct { // Current link state float angle; // Link configuration uint32_t length; int32_t zero_rotate; int32_t min_angle; int32_t max_angle; } link_info_t; typedef struct { point_3d_t position; path_3d_t movement_path; link_info_t links[3]; } limb_info_t; // *************************************************************************** /// @brief Calculate angles /// @param info: limb info @ref limb_info_t /// @return true - calculation success, false - no // *************************************************************************** static bool kinematic_calculate_angles(limb_info_t* info) { int32_t coxa_zero_rotate_deg = info->links[LINK_COXA].zero_rotate; int32_t femur_zero_rotate_deg = info->links[LINK_FEMUR].zero_rotate; int32_t tibia_zero_rotate_deg = info->links[LINK_TIBIA].zero_rotate; uint32_t coxa_length = info->links[LINK_COXA].length; uint32_t femur_length = info->links[LINK_FEMUR].length; uint32_t tibia_length = info->links[LINK_TIBIA].length; float x = info->position.x; float y = info->position.y; float z = info->position.z; // Move to (X*, Y*, Z*) coordinate system - rotate float coxa_zero_rotate_rad = DEG_TO_RAD(coxa_zero_rotate_deg); float x1 = x * cos(coxa_zero_rotate_rad) + z * sin(coxa_zero_rotate_rad); float y1 = y; float z1 = -x * sin(coxa_zero_rotate_rad) + z * cos(coxa_zero_rotate_rad); // // Calculate COXA angle // float coxa_angle_rad = atan2(z1, x1); info->links[LINK_COXA].angle = RAD_TO_DEG(coxa_angle_rad); // // Prepare for calculation FEMUR and TIBIA angles // // Move to (X*, Y*) coordinate system (rotate on axis Y) x1 = x1 * cos(coxa_angle_rad) + z1 * sin(coxa_angle_rad); // Move to (X**, Y**) coordinate system (remove coxa from calculations) x1 = x1 - coxa_length; // Calculate angle between axis X and destination point float fi = atan2(y1, x1); // Calculate distance to destination point float d = sqrt(x1 * x1 + y1 * y1); if (d > femur_length + tibia_length) { return false; // Point not attainable } // // Calculate triangle angles // float a = tibia_length; float b = femur_length; float c = d; float alpha = acos( (b * b + c * c - a * a) / (2 * b * c) ); float gamma = acos( (a * a + b * b - c * c) / (2 * a * b) ); // // Calculate FEMUR and TIBIA angle // info->links[LINK_FEMUR].angle = femur_zero_rotate_deg - RAD_TO_DEG(alpha) - RAD_TO_DEG(fi); info->links[LINK_TIBIA].angle = RAD_TO_DEG(gamma) - tibia_zero_rotate_deg; // // Check angles // if (info->links[LINK_COXA].angle < info->links[LINK_COXA].min_angle || info->links[LINK_COXA].angle > info->links[LINK_COXA].max_angle) { return false; } if (info->links[LINK_FEMUR].angle < info->links[LINK_FEMUR].min_angle || info->links[LINK_FEMUR].angle > info->links[LINK_FEMUR].max_angle) { return false; } if (info->links[LINK_TIBIA].angle < info->links[LINK_TIBIA].min_angle || info->links[LINK_TIBIA].angle > info->links[LINK_TIBIA].max_angle) { return false; } return true; }

कार्रवाई में एल्गोरिदम

फिर, संयोग से, एक अनुक्रम दिखाई दिया जो कुछ हद तक एक नृत्य की याद दिलाता था

पुनश्च

मुझे खुशी होगी अगर कोई भी इस एल्गोरिथम को सरल बना सके। मैंने इसे इसलिए बनाया ताकि मैं इसे समझ सकूं, कहो, आधा साल।

खरोंच से हेक्सापोड विकसित करना (भाग 3) - कीनेमेटीक्स