PyTorch में विज़ुअलाइज़ेशन के माध्यम से दृढ़ तंत्रिका नेटवर्क को समझना

हमारे युग में, मशीनों ने छवियों में सुविधाओं और वस्तुओं को समझने और परिभाषित करने में 99% सटीकता हासिल की है। हमें हर दिन इसका सामना करना पड़ता है, उदाहरण के लिए: स्मार्टफोन के कैमरे में चेहरा पहचानना, गूगल पर तस्वीरों की खोज करने की क्षमता, बार कोड से टेक्स्ट को स्कैन करना या अच्छी गति से किताबें इत्यादि। इस तरह की मशीन दक्षता को विशेष प्रकार के तंत्रिका संबंधी धन्यवाद के कारण संभव बनाया गया, जिसे दिवालात्मक तंत्रिका कहा जाता है। नेटवर्क। यदि आप एक गहरी शिक्षा के प्रति उत्साही हैं, तो आपने शायद इसके बारे में सुना है, और आप कई छवि वर्गीकरण विकसित कर सकते हैं। Tensorflow और PyTorch जैसे आधुनिक गहरे शिक्षण ढांचे छवि मशीन सीखने को सरल बनाते हैं। हालांकि, यह सवाल अभी भी बना हुआ है: डेटा तंत्रिका नेटवर्क की परतों से कैसे गुजरता है और कंप्यूटर उनसे कैसे सीखता है? खरोंच से स्पष्ट दृश्य प्राप्त करने के लिए, हम प्रत्येक परत की छवि को देखते हुए, एक दृढ़ संकल्प में गोता लगाते हैं।

संवादी तंत्रिका नेटवर्क

इससे पहले कि आप दृढ़ तंत्रिका नेटवर्क (SNA) का अध्ययन करना शुरू करें, आपको यह सीखना होगा कि तंत्रिका नेटवर्क के साथ कैसे काम किया जाए। तंत्रिका नेटवर्क जटिल समस्याओं को हल करने और डेटा में पैटर्न की खोज करने के लिए मानव मस्तिष्क की नकल करते हैं। पिछले कुछ वर्षों में, उन्होंने कई मशीन लर्निंग और कंप्यूटर विज़न एल्गोरिदम को बदल दिया है। एक तंत्रिका नेटवर्क के मूल मॉडल में परतों में आयोजित न्यूरॉन्स होते हैं। प्रत्येक तंत्रिका नेटवर्क में एक इनपुट और आउटपुट परत होती है और समस्या की जटिलता के आधार पर कई छिपी हुई परतें इसमें जोड़ी जाती हैं। परतों के माध्यम से डेटा संचारित करते समय, न्यूरॉन्स प्रशिक्षित होते हैं और संकेतों को पहचानते हैं। तंत्रिका नेटवर्क के इस प्रतिनिधित्व को एक मॉडल कहा जाता है। मॉडल के प्रशिक्षित होने के बाद, हम नेटवर्क को परीक्षण डेटा के आधार पर पूर्वानुमान बनाने के लिए कहते हैं।

एसएनएस एक विशेष प्रकार का तंत्रिका नेटवर्क है जो छवियों के साथ अच्छी तरह से काम करता है। इयान लेकुन ने उन्हें 1998 में प्रस्तावित किया, जहां उन्होंने इनपुट छवि में मौजूद संख्या को मान्यता दी। SNA का उपयोग वाक् पहचान, छवि विभाजन और पाठ प्रसंस्करण के लिए भी किया जाता है। कनफ्यूजनियल न्यूरल नेटवर्क के निर्माण से पहले, छवि क्लासिफायरियर के निर्माण में बहुपरत पर्सेप्ट्रोन्स का उपयोग किया गया था। छवि वर्गीकरण एक मल्टीचैनल (रंग, काले और सफेद) रेखापुंज छवि से कक्षाएं निकालने के कार्य को संदर्भित करता है। बहुपरत पेसेप्ट्रॉन को छवियों में जानकारी खोजने में लंबा समय लगता है, क्योंकि प्रत्येक इनपुट को अगली परत में प्रत्येक न्यूरॉन के साथ जुड़ा होना चाहिए। एसएनए स्थानीय कनेक्टिविटी नामक एक अवधारणा का उपयोग करके उनके चारों ओर चला गया। इसका मतलब है कि हम प्रत्येक न्यूरॉन को केवल स्थानीय इनपुट क्षेत्र से जोड़ेंगे। यह मापदंडों की संख्या को कम करता है, जिससे नेटवर्क के विभिन्न हिस्सों को उच्च-स्तरीय विशेषताओं जैसे कि बनावट या दोहराव पैटर्न में विशेषज्ञता प्राप्त करने की अनुमति मिलती है। उलझन में? आइए तुलना करें कि छवियों को मल्टी-लेयर परसेप्ट्रोन (एमपी) और कन्वेन्शनल न्यूरल नेटवर्क के माध्यम से कैसे प्रसारित किया जाता है।

MP और SNA की तुलना

बहुपरत परसेप्ट्रॉन के लिए इनपुट परत में प्रविष्टियों की कुल संख्या 784 होगी, क्योंकि इनपुट छवि का आकार 28x28 = 784 (MNIST डेटासेट माना जाता है) है। नेटवर्क को इनपुट छवि पर संख्या का अनुमान लगाने में सक्षम होना चाहिए, जिसका अर्थ है कि आउटपुट 0 से 9 तक की रेंज में निम्न में से किसी भी वर्ग से संबंधित हो सकता है। आउटपुट परत में, हम वर्ग अनुमान लौटाते हैं, कहते हैं कि क्या यह इनपुट नंबर "3" के साथ छवि है। फिर उत्पादन परत में इसी न्यूरॉन "3" का अन्य न्यूरॉन्स की तुलना में अधिक मूल्य होता है। फिर से सवाल उठता है: "हमें कितनी छिपी हुई परतों की आवश्यकता है और प्रत्येक में कितने न्यूरॉन्स होने चाहिए?" उदाहरण के लिए, निम्न MP कोड लें:



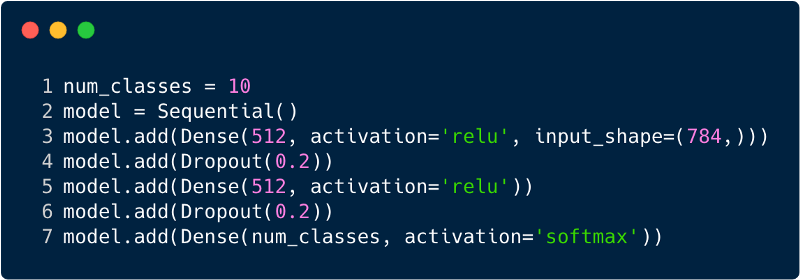
उपरोक्त कोड केरस नामक एक रूपरेखा का उपयोग करके लागू किया गया है। पहली छिपी हुई परत में 512 न्यूरॉन्स होते हैं जो 784 न्यूरॉन्स की इनपुट परत से जुड़े होते हैं। अगली छिपी हुई परत: अपवर्जन परत, जो रिट्रेनिंग की समस्या को हल करती है। 0.2 का मतलब है कि पिछली छिपी हुई परत के न्यूरॉन्स को ध्यान में नहीं रखने का 20% मौका है। हमने फिर से एक दूसरी छिपी हुई परत को पहले छिपे हुए परत (512) के समान न्यूरॉन्स के साथ जोड़ा, और फिर एक और विशेष परत को जोड़ा। अंत में, 10 वर्गों से युक्त आउटपुट परत के साथ परतों के इस सेट को समाप्त करना। वह वर्ग जो सबसे अधिक मायने रखता है वह मॉडल द्वारा अनुमानित संख्या होगी। यह है कि सभी परतों की पहचान करने के बाद एक बहुपरत नेटवर्क कैसा दिखता है। मल्टी-लेवल परसेप्ट्रॉन की कमियों में से एक यह है कि यह पूरी तरह से जुड़ा हुआ है, जिसमें बहुत समय और स्थान लगता है।



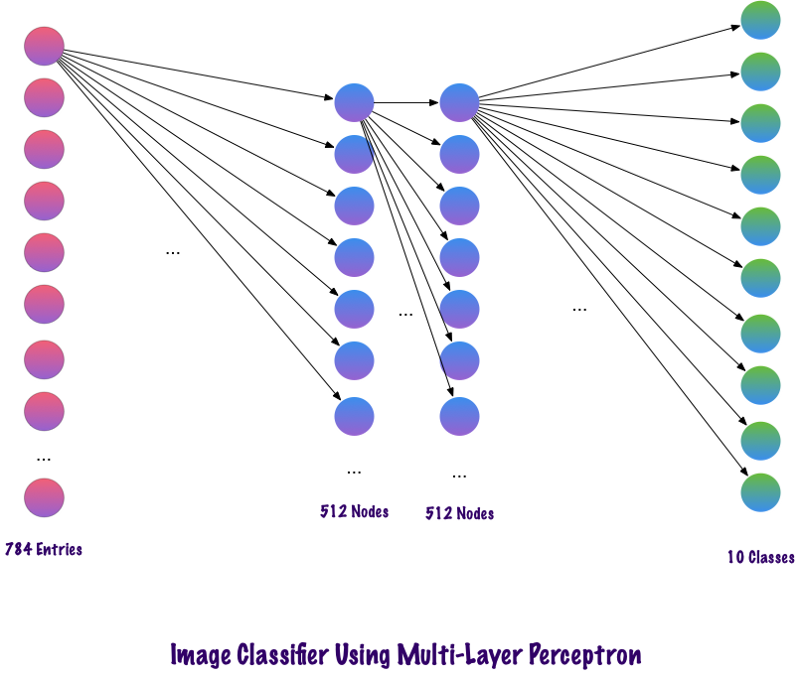
बातचीत पूरी तरह से जुड़े परतों का उपयोग नहीं करते हैं। वे विरल परतों का उपयोग करते हैं, जो इनपुट के रूप में मैट्रीस लेते हैं, जो एमपी पर एक लाभ देता है। एमपी में, प्रत्येक नोड पूरी तस्वीर को समझने के लिए जिम्मेदार है। एसएनए में, हम छवि को क्षेत्रों (पिक्सेल के छोटे स्थानीय क्षेत्रों) में तोड़ते हैं। आउटपुट लेयर पैटर्न को खोजने के लिए प्रत्येक छिपे हुए नोड से प्राप्त डेटा को जोड़ती है। नीचे एक छवि है कि परतें कैसे जुड़ी हुई हैं।



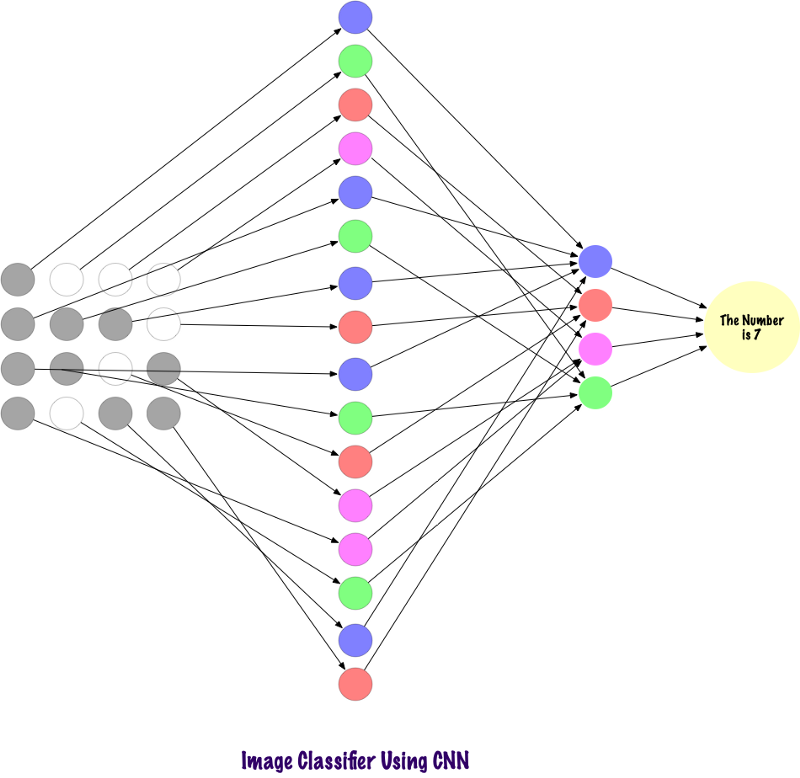
अब देखते हैं कि एसएनए तस्वीरों में कैसे जानकारी पाते हैं। इससे पहले, हमें यह समझने की आवश्यकता है कि संकेत कैसे निकाले जाते हैं। एसएनए में, हम विभिन्न परतों का उपयोग करते हैं, प्रत्येक परत छवि के संकेतों को संरक्षित करती है, उदाहरण के लिए, यह कुत्ते की छवि को ध्यान में रखता है, जब नेटवर्क को कुत्ते को वर्गीकृत करने की आवश्यकता होती है, तो उसे सभी संकेतों, जैसे आंख, कान, जीभ, पैर, आदि की पहचान करनी चाहिए। इन संकेतों को फ़िल्टर और कोर का उपयोग करके स्थानीय नेटवर्क स्तरों पर तोड़ा और पहचाना जाता है।

कंप्यूटर एक छवि को कैसे देखते हैं?

छवि को देखने और इसके अर्थ को समझने वाला व्यक्ति बहुत ही उचित लगता है। मान लीजिए कि आप चलते हैं, और अपने आसपास के कई परिदृश्यों को देखते हैं। हम इस मामले में प्रकृति को कैसे समझते हैं? हम अपने मुख्य अर्थ अंग - आंख का उपयोग करके पर्यावरण की तस्वीरें लेते हैं, और फिर इसे रेटिना पर भेजते हैं। यह सब बहुत दिलचस्प लगता है, है ना? अब आइए कल्पना करें कि एक कंप्यूटर भी ऐसा ही करता है। कंप्यूटर में, छवियों की व्याख्या पिक्सेल मूल्यों के एक सेट का उपयोग करके की जाती है जो 0 से 255 तक होते हैं। कंप्यूटर इन पिक्सेल मूल्यों को देखता है और उन्हें समझता है। पहली नज़र में, वह वस्तुओं और रंगों को नहीं जानता है। यह बस पिक्सेल मूल्यों को पहचानता है, और छवि कंप्यूटर के लिए पिक्सेल मूल्यों के एक सेट के बराबर है। बाद में, पिक्सेल मूल्यों का विश्लेषण करके, वह धीरे-धीरे सीखता है कि क्या छवि ग्रे या रंग है। ग्रेस्केल में छवियों का केवल एक चैनल होता है, क्योंकि प्रत्येक पिक्सेल एक रंग की तीव्रता का प्रतिनिधित्व करता है। 0 का अर्थ है काला, और 255 का अर्थ है सफेद, काले और सफेद के अन्य प्रकार, अर्थात्, ग्रे, उनके बीच हैं।

रंग चित्रों में तीन चैनल होते हैं, लाल, हरा और नीला। वे 3 रंगों (तीन आयामी मैट्रिक्स) की तीव्रता का प्रतिनिधित्व करते हैं, और जब मूल्य एक साथ बदलते हैं, तो यह रंगों का एक बड़ा सेट देता है, वास्तव में एक रंग पैलेट! उसके बाद, कंप्यूटर छवि में वस्तुओं के घटता और आकृति को पहचानता है। यह सब दृढ़ तंत्रिका नेटवर्क में अध्ययन किया जा सकता है। इसके लिए हम डेटासेट लोड करने और छवियों पर फ़िल्टर लागू करने के लिए PyTorch का उपयोग करेंगे। निम्नलिखित कोड का एक स्निपेट है।

# Load the libraries import torch import numpy as np from torchvision import datasets import torchvision.transforms as transforms # Set the parameters num_workers = 0 batch_size = 20 # Converting the Images to tensors using Transforms transform = transforms.ToTensor() train_data = datasets.MNIST(root='data', train=True, download=True, transform=transform) test_data = datasets.MNIST(root='data', train=False, download=True, transform=transform) # Loading the Data train_loader = torch.utils.data.DataLoader(train_data, batch_size=batch_size, num_workers=num_workers) test_loader = torch.utils.data.DataLoader(test_data, batch_size=batch_size, num_workers=num_workers) import matplotlib.pyplot as plt %matplotlib inline dataiter = iter(train_loader) images, labels = dataiter.next() images = images.numpy() # Peeking into dataset fig = plt.figure(figsize=(25, 4)) for image in np.arange(20): ax = fig.add_subplot(2, 20/2, image+1, xticks=[], yticks=[]) ax.imshow(np.squeeze(images[image]), cmap='gray') ax.set_title(str(labels[image].item())) 

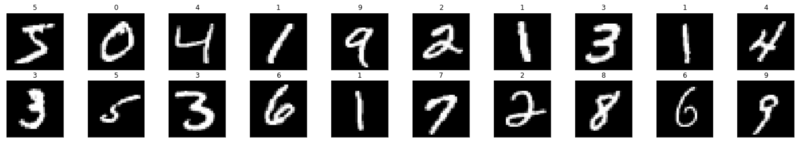
अब देखते हैं कि एक एकल छवि तंत्रिका नेटवर्क में कैसे खिलाया जाता है।

 img = np.squeeze(images[7]) fig = plt.figure(figsize = (12,12)) ax = fig.add_subplot(111) ax.imshow(img, cmap='gray') width, height = img.shape thresh = img.max()/2.5 for x in range(width): for y in range(height): val = round(img[x][y],2) if img[x][y] !=0 else 0 ax.annotate(str(val), xy=(y,x), color='white' if img[x][y]<thresh else 'black') 

यह कैसे "संख्या" पिक्सेल में टूट गया है। हस्तलिखित अंकों के सेट से, "3" को यादृच्छिक रूप से चुना जाता है, जिसमें पिक्सेल मान प्रदर्शित होते हैं। यहाँ ToTensor () वास्तविक पिक्सेल मान (0–255) को सामान्य करता है और उन्हें 0 से 1. तक सीमित करता है। यह क्यों है? क्योंकि यह बाद के वर्गों में गणना की सुविधा प्रदान करता है, या तो छवियों की व्याख्या करने के लिए, या उनमें मौजूद सामान्य पैटर्न खोजने के लिए।

अपना खुद का फ़िल्टर बनाएं

फ़िल्टर, जैसा कि नाम से पता चलता है, फ़िल्टर जानकारी। सजातीय तंत्रिका नेटवर्क के मामले में, जब छवियों के साथ काम करते हैं, तो पिक्सल के बारे में जानकारी फ़िल्टर की जाती है। हमें क्यों फ़िल्टर करना चाहिए? याद रखें कि एक कंप्यूटर को छवियों को समझने के लिए एक सीखने की प्रक्रिया से गुजरना चाहिए, यह बहुत ही समान है कि बच्चा कैसे करता है। इस मामले में, हालांकि, हमें कई वर्षों की आवश्यकता नहीं होगी! संक्षेप में, वह खरोंच से सीखता है और फिर पूरे को आगे बढ़ाता है।

इसलिए, नेटवर्क को शुरुआत में छवि के सभी मोटे हिस्सों, जैसे कि किनारों, आकृति और अन्य निम्न-स्तरीय तत्वों को जानना चाहिए। एक बार जब उन्हें पता चलता है, तो जटिल लक्षणों के लिए मार्ग प्रशस्त होता है। उन्हें प्राप्त करने के लिए, हमें पहले निम्न-स्तरीय विशेषताओं को निकालना होगा, फिर मध्य को, और फिर उच्च-स्तरीय लोगों को। फिल्टर जानकारी को निकालने का एक तरीका है जो उपयोगकर्ता को चाहिए, न कि केवल अंधे डेटा ट्रांसफर के कारण, क्योंकि कंप्यूटर छवियों की संरचना को नहीं समझता है। शुरुआत में, एक विशिष्ट फिल्टर के आधार पर निम्न-स्तरीय कार्यों को निकाला जा सकता है। यहां फिल्टर भी छवि के समान पिक्सेल मानों का एक सेट है। इसे उन वज़न के रूप में समझा जा सकता है जो कि परतदार तंत्रिका नेटवर्क में परतों को जोड़ते हैं। इन वज़न या फ़िल्टर को मध्यवर्ती मानों को उत्पन्न करने के लिए इनपुट मानों से गुणा किया जाता है जो छवि की कंप्यूटर समझ का प्रतिनिधित्व करते हैं। फिर उन्हें दृश्य का विस्तार करने के लिए कुछ और फिल्टर द्वारा गुणा किया जाता है। फिर यह एक व्यक्ति के दृश्य अंगों का पता लगाता है (बशर्ते कि कोई व्यक्ति छवि में मौजूद है)। बाद में, कई और फिल्टर और कई परतों को शामिल करने के साथ, कंप्यूटर ने कहा: "ओह, हाँ! यह एक आदमी है। ”

अगर हम फ़िल्टर के बारे में बात करते हैं, तो हमारे पास कई विकल्प हैं। आप छवि को धुंधला करना चाहते हैं, फिर एक धब्बा फ़िल्टर लागू कर सकते हैं, यदि आपको तीखेपन को जोड़ने की आवश्यकता है, तो एक तीक्ष्णता फ़िल्टर बचाव में आएगी, आदि।

आइए फिल्टर की कार्यक्षमता को समझने के लिए कुछ कोड स्निपेट देखें।









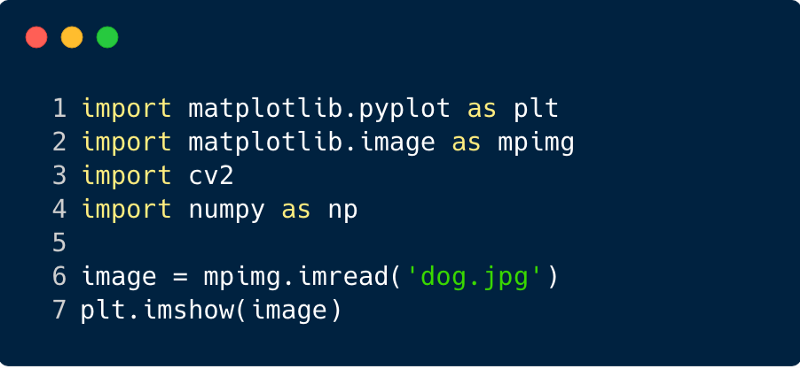
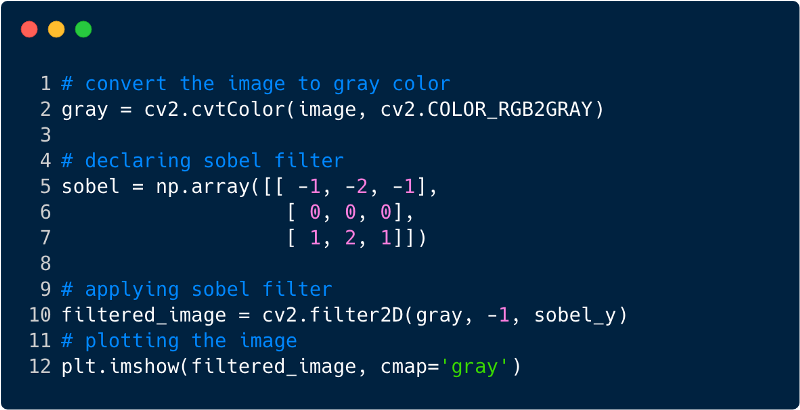
फ़िल्टर को लागू करने के बाद छवि कैसी दिखती है, इस मामले में हमने सोबेल फ़िल्टर का उपयोग किया।

संवादी तंत्रिका नेटवर्क

अब तक, हमने देखा है कि छवियों से सुविधाओं को निकालने के लिए फ़िल्टर का उपयोग कैसे किया जाता है। अब, संपूर्ण कनैक्शनल न्यूरल नेटवर्क को पूरा करने के लिए, हमें उन सभी परतों के बारे में जानना होगा जो हम इसे डिजाइन करने के लिए उपयोग करते हैं। SNA में उपयोग की गई परतें,

1. संवादी परत
2. पूलिंग परत
3. पूरी तरह से बंधी हुई परत

सभी तीन परतों के साथ, दृढ़ छवि वर्गीकरण इस तरह दिखता है:



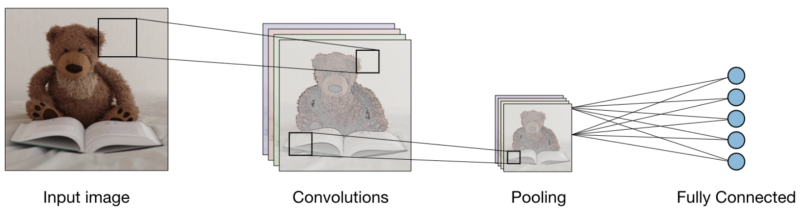
अब देखते हैं कि प्रत्येक परत क्या करती है।

कन्वेन्शियल लेयर (CONV) उन फिल्टर का उपयोग करता है जो इनपुट इमेज को स्कैन करके कनवल्शन ऑपरेशन करते हैं। इसके हाइपरपरमेटर्स में एक फिल्टर आकार शामिल है, जो 2x2, 3x3, 4x4, 5x5 (लेकिन यह तक सीमित नहीं है) हो सकता है और चरण एस। परिणाम ओ को एक फीचर मैप या एक सक्रियण मानचित्र कहा जाता है जिसमें सभी विशेषताओं की गणना इनपुट परतों और फिल्टर का उपयोग करके की जाती है। नीचे कनवल्शन लागू करते समय फीचर मैप्स की पीढ़ी की एक छवि है,



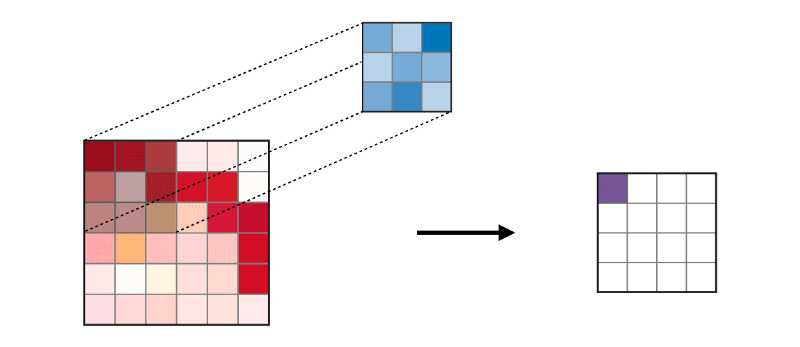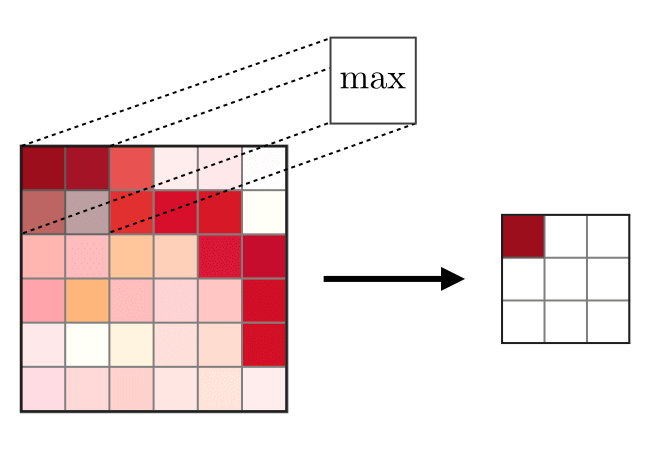
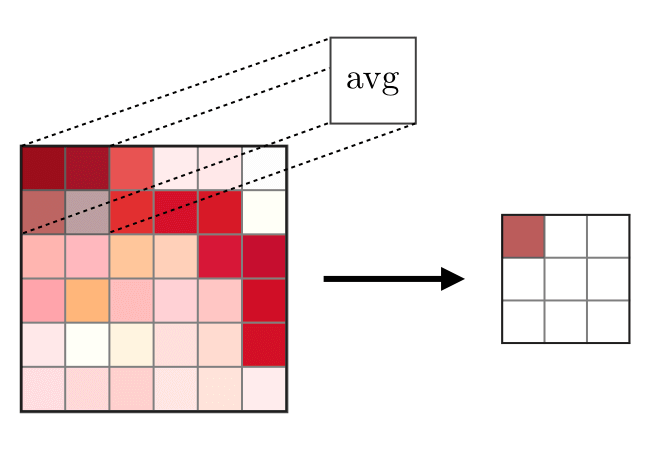
मर्जिंग लेयर (POOL) का उपयोग आमतौर पर कन्वेंशन लेयर के बाद उपयोग की जाने वाली सुविधाओं को कॉम्पैक्ट करने के लिए किया जाता है। दो प्रकार के संघ संचालन हैं - यह अधिकतम और औसत संघ है, जहां विशेषताओं के अधिकतम और औसत मूल्य क्रमशः लिए जाते हैं। निम्नलिखित मर्ज संचालन का कार्य है,





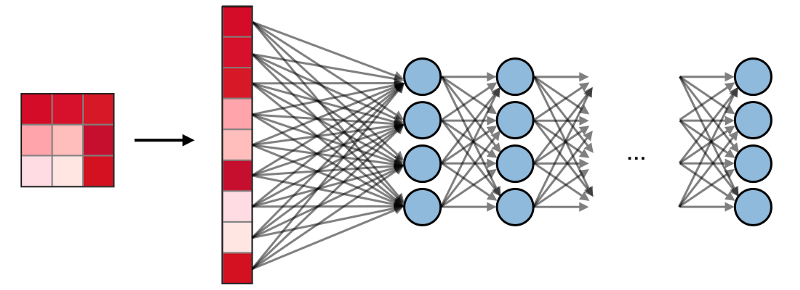
पूरी तरह से जुड़ी हुई परतें (एफसी) एक फ्लैट इनपुट के साथ संचालित होती हैं, जहां प्रत्येक इनपुट सभी न्यूरॉन्स से जुड़ा होता है। वे आम तौर पर नेटवर्क के अंत में आउटपुट लेयर से छिपी हुई परतों को जोड़ने के लिए उपयोग किए जाते हैं, जो वर्ग स्कोर को अनुकूलित करने में मदद करता है।

PyTorch में SNA दृश्य

अब जब हमारे पास SNA के निर्माण की पूरी विचारधारा है, तो आइए फेसबुक से PyTorch ढांचे का उपयोग करके SNA को लागू करें।

चरण 1 : नेटवर्क पर भेजे जाने के लिए इनपुट छवि डाउनलोड करें। (यहाँ हम इसे Numpy और OpenCV के साथ करते हैं)

 import cv2 import matplotlib.pyplot as plt %matplotlib inline img_path = 'dog.jpg' bgr_img = cv2.imread(img_path) gray_img = cv2.cvtColor(bgr_img, cv2.COLOR_BGR2GRAY) # Normalise gray_img = gray_img.astype("float32")/255 plt.imshow(gray_img, cmap='gray') plt.show() 

चरण 2 : रेंडर फिल्टर

आइए फ़िल्टर को बेहतर ढंग से समझने के लिए कल्पना करें कि हम किसका उपयोग करेंगे,

 import numpy as np filter_vals = np.array([ [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1], [-1, -1, 1, 1] ]) print('Filter shape: ', filter_vals.shape) # Defining the Filters filter_1 = filter_vals filter_2 = -filter_1 filter_3 = filter_1.T filter_4 = -filter_3 filters = np.array([filter_1, filter_2, filter_3, filter_4]) # Check the Filters fig = plt.figure(figsize=(10, 5)) for i in range(4): ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[]) ax.imshow(filters[i], cmap='gray') ax.set_title('Filter %s' % str(i+1)) width, height = filters[i].shape for x in range(width): for y in range(height): ax.annotate(str(filters[i][x][y]), xy=(y,x), color='white' if filters[i][x][y]<0 else 'black') 

चरण 3 : SNA निर्धारित करें

इस SNA में एक अल्टीमेटल लेयर और एक पूलिंग लेयर है, जिसमें अधिकतम फंक्शन है, और वेट्स को ऊपर दिखाए गए फिल्टर्स का उपयोग करके इनिशियलाइज़ किया जाता है।

 import torch import torch.nn as nn import torch.nn.functional as F class Net(nn.Module): def __init__(self, weight): super(Net, self).__init__() # initializes the weights of the convolutional layer to be the weights of the 4 defined filters k_height, k_width = weight.shape[2:] # assumes there are 4 grayscale filters self.conv = nn.Conv2d(1, 4, kernel_size=(k_height, k_width), bias=False) # initializes the weights of the convolutional layer self.conv.weight = torch.nn.Parameter(weight) # define a pooling layer self.pool = nn.MaxPool2d(2, 2) def forward(self, x): # calculates the output of a convolutional layer # pre- and post-activation conv_x = self.conv(x) activated_x = F.relu(conv_x) # applies pooling layer pooled_x = self.pool(activated_x) # returns all layers return conv_x, activated_x, pooled_x # instantiate the model and set the weights weight = torch.from_numpy(filters).unsqueeze(1).type(torch.FloatTensor) model = Net(weight) # print out the layer in the network print(model) 

 Net( (conv): Conv2d(1, 4, kernel_size=(4, 4), stride=(1, 1), bias=False) (pool): MaxPool2d(kernel_size=2, stride=2, padding=0, dilation=1, ceil_mode=False) ) 

चरण 4 : रेंडर फिल्टर
उपयोग किए गए फ़िल्टर पर एक त्वरित नज़र,

 def viz_layer(layer, n_filters= 4): fig = plt.figure(figsize=(20, 20)) for i in range(n_filters): ax = fig.add_subplot(1, n_filters, i+1) ax.imshow(np.squeeze(layer[0,i].data.numpy()), cmap='gray') ax.set_title('Output %s' % str(i+1)) fig = plt.figure(figsize=(12, 6)) fig.subplots_adjust(left=0, right=1.5, bottom=0.8, top=1, hspace=0.05, wspace=0.05) for i in range(4): ax = fig.add_subplot(1, 4, i+1, xticks=[], yticks=[]) ax.imshow(filters[i], cmap='gray') ax.set_title('Filter %s' % str(i+1)) gray_img_tensor = torch.from_numpy(gray_img).unsqueeze(0).unsqueeze(1) 

फिल्टर:



चरण 5 : परत द्वारा फ़िल्टर किए गए परिणाम

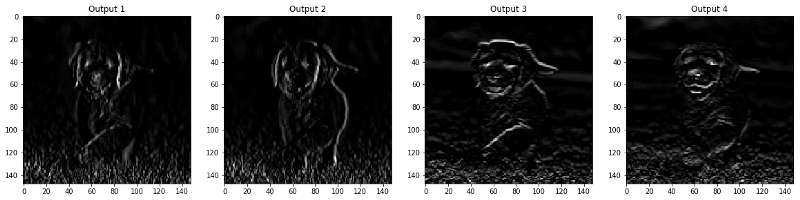
CONV और POOL लेयर में दिखाई देने वाली इमेज को नीचे दिखाया गया है।

 viz_layer(activated_layer) viz_layer(pooled_layer) 

संवादी परतें



पूलिंग लेयर्स


स्रोत