खरोंच से XGBoost लिखना - भाग 1: निर्णय पेड़

नमस्कार, हेब्र!

निर्णय लेने वाले पेड़ों के बारे में उच्च गुणवत्ता वाले गाइडों के लिए कई खोज के बाद और प्रोग्रामिंग भाषाओं में उनके प्रत्यक्ष कार्यान्वयन के साथ एल्गोरिदम (बूस्टिंग, निर्णय वन, आदि) और बिना कुछ पाए (जो कोई भी इसे पाता है, टिप्पणियों में लिखें, शायद मैं कुछ नया सीखूंगा), मैंने अपना खुद का नेतृत्व करने का फैसला किया, जैसा कि मैं इसे देखना चाहूंगा। शब्दों में कार्य सरल है, लेकिन, जैसा कि आप जानते हैं, शैतान छोटी चीजों में है, जिनमें से पेड़ों के लिए बहुत सारे एल्गोरिदम हैं।

चूंकि विषय काफी व्यापक है, इसलिए एक लेख में सब कुछ फिट करना बहुत मुश्किल होगा, इसलिए दो प्रकाशन होंगे: पहला पेड़ों के लिए समर्पित है, और दूसरा भाग ढाल बूस्टिंग एल्गोरिदम के कार्यान्वयन के लिए समर्पित होगा। यहां प्रस्तुत सभी सामग्री खुले स्रोतों, मेरे कोड, सहयोगियों और दोस्तों के कोड के आधार पर संकलित और डिज़ाइन की गई है। मैं आपको तुरंत चेतावनी देता हूं, बहुत सारे कोड होंगे।



तो आपको क्या जानने की ज़रूरत है और यह जानने में सक्षम हैं कि खरोंच से निर्णय पेड़ों के साथ अपने स्वयं के पहनावा एल्गोरिदम कैसे लिखें? चूंकि एल्गोरिदम का एक पहनावा "कमजोर एल्गोरिदम" की रचना से ज्यादा कुछ नहीं है, एक अच्छा पहनावा लिखने के लिए अच्छे "कमजोर एल्गोरिदम" की आवश्यकता होती है, हम इस लेख में विस्तार से उनका विश्लेषण करेंगे। जैसा कि नाम से पता चलता है, ये महत्वपूर्ण पेड़ हैं, और सरल से जटिल तक बढ़ते हुए, हम उन्हें लिखना सीखेंगे। इस मामले में, जोर सीधे कार्यान्वयन पर रखा जाएगा, पूरे सिद्धांत को न्यूनतम रूप से प्रस्तुत किया जाएगा, मूल रूप से मैं स्वतंत्र अध्ययन के लिए सामग्रियों के लिंक दूंगा।

सामग्री को सीखने के लिए, आपको यह समझने की आवश्यकता है कि हमारा एल्गोरिथ्म कितना अच्छा या बुरा है। हम बहुत सरल रूप से समझेंगे - हम कुछ विशिष्ट डेटा सेट को ठीक करेंगे और हम अपने एल्गोरिदम की तुलना स्केलेर (पेड़ों के एल्गोरिदम से करेंगे, जो इस पुस्तकालय के बिना क्या होगा)। हम बहुत तुलना करेंगे: एल्गोरिथ्म की जटिलता, डेटा पर मीट्रिक, अपटाइम, आदि।

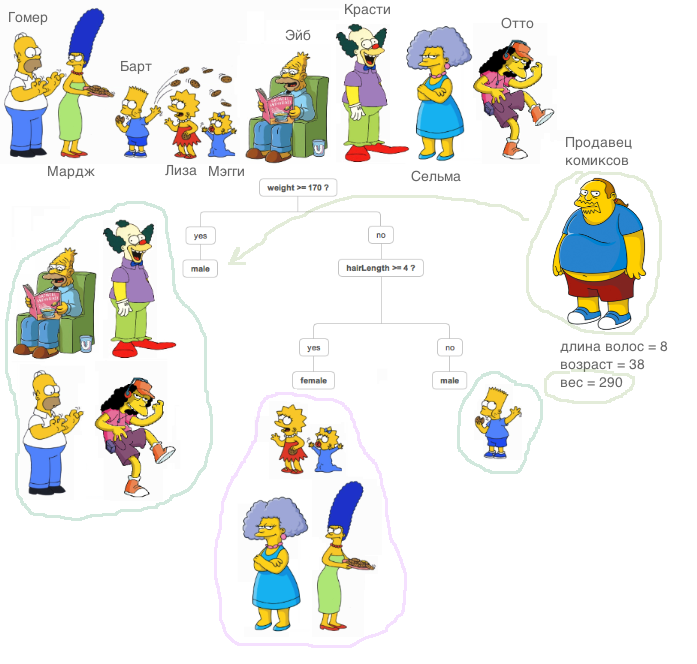
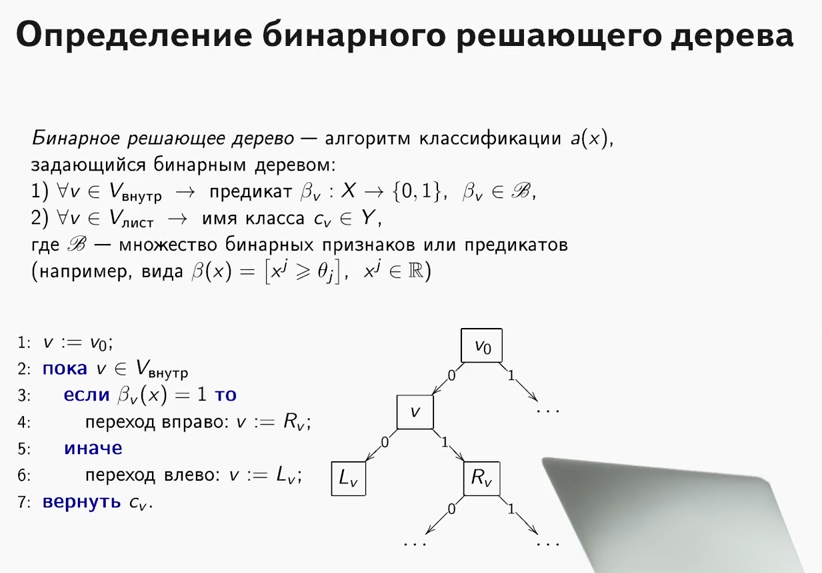
एक निर्णायक पेड़ क्या है? एक बहुत अच्छी सामग्री, जहां निर्णय वृक्ष के सिद्धांत को समझाया गया है, ओडीएस पाठ्यक्रम में निहित है (वैसे, एक शांत पाठ्यक्रम, मैं उन लोगों को सलाह देता हूं जो एमएल के साथ अपने परिचितों को शुरू करते हैं)।

एक बहुत महत्वपूर्ण स्पष्टीकरण: नीचे वर्णित सभी मामलों में, सभी संकेत वास्तविक होंगे, हम एल्गोरिदम के बाहर डेटा के साथ विशेष परिवर्तन नहीं करेंगे (हम एल्गोरिदम की तुलना करते हैं, डेटासेट नहीं)।

अब आइए जानें कि निर्णय पेड़ों का उपयोग करके प्रतिगमन की समस्या को कैसे हल किया जाए। हम एंट्री के रूप में MSE मीट्रिक का उपयोग करेंगे।

हम एक बहुत ही सरल RegressionTree वर्ग को लागू करते हैं, जो एक पुनरावर्ती दृष्टिकोण पर आधारित है। जानबूझकर, हम एक बहुत ही अप्रभावी के साथ शुरू करते हैं, लेकिन भविष्य में इसे सुधारने में सक्षम होने के लिए ऐसी कक्षा के कार्यान्वयन को समझना आसान है।

1. रेग्रेशनट्री () वर्ग

 class RegressionTree(): '''  RegressionTree   .    ,      . ''' def __init__(self, max_depth=3, n_epoch=10, min_size=8): '''   . ''' self.max_depth = max_depth #   self.min_size = min_size #    self.value = 0 #    (   ) self.feature_idx = -1 #    self.feature_threshold = 0 #    self.left = None #   self.right = None #   def fit(self, X, y): '''   .     . ''' #    self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #       prev_error_left = base_error prev_error_right = 0 #     0 -  if self.max_depth <= 1: return dim_shape = X.shape[1] #       left_value = 0 right_value = 0 #     for feat in range(dim_shape): #   idxs = np.argsort(X[:, feat]) #        N = X.shape[0] N1, N2 = N, 0 thres = 1 #      while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #    if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue # ,         target_right = y[idxs][:thres] target_left = y[idxs][thres:] mean_right = y[idxs][:thres].mean(), mean_left = y[idxs][thres:].mean() #        - #   (  ) left_shape = target_left.shape[0] right_shape = target_right.shape[0] mean_left_array = [mean_left for _ in range(left_shape)] mean_right_array = [mean_right for _ in range(right_shape)] #      prev_error_left = N1/N * mse(target_left, mean_left_array) prev_error_right = N2/N * mse(target_right, mean_right_array) #    ,   if (prev_error_left + prev_error_right < error): if (min(N1,N2) > self.min_size): self.feature_idx = feat self.feature_threshold = x left_value = mean_left right_value = mean_right flag = 1 error = prev_error_left + prev_error_right thres += 1 #     ,  if self.feature_idx == -1: return #   -   ,    #   -     self.left = RegressionTree(self.max_depth - 1) self.left.value = left_value self.right = RegressionTree(self.max_depth - 1) self.right.value = right_value #   idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #  self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): '''     -  ,         self.value -    . ''' if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): '''    -      __predict(). ''' y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

मैं संक्षेप में बताऊंगा कि प्रत्येक विधि यहाँ क्या करती है।

fit विधि, जैसा कि नाम से पता चलता है, मॉडल सिखाता है। एक प्रशिक्षण नमूना इनपुट पर लागू होता है और एक पेड़ प्रशिक्षण प्रक्रिया होती है। संकेतों को mse , हम इस मामले में एन्ट्रापी को कम करने के मामले में पेड़ के सबसे अच्छे विभाजन की तलाश कर रहे हैं। यह निर्धारित करने के लिए कि एक अच्छा विभाजन ढूंढना संभव था बहुत सरल है, यह दो शर्तों को पूरा करने के लिए पर्याप्त है। हम नहीं चाहते हैं कि कुछ वस्तुएं विभाजन में गिर जाएं ( mse देने के लिए सुरक्षा), और mse लिए औसत त्रुटि उस त्रुटि से कम होनी चाहिए जो अब पेड़ में है - हम सूचना लाभ में उसी लाभ की तलाश कर रहे हैं। इस तरह से सभी संकेतों और सभी विशिष्ट मूल्यों से गुजरने के बाद, हम सभी विकल्पों से गुजरेंगे और सबसे अच्छे विभाजन का चयन करेंगे। और फिर हम प्राप्त विभाजन पर एक पुनरावर्ती कॉल करते हैं जब तक कि पुनरावृत्ति से बाहर निकलने की शर्तों को संतुष्ट नहीं किया जाता है।

__predict विधि, जैसा कि नाम का अर्थ है, एक विधेय बनाता है। एक इनपुट के रूप में एक वस्तु प्राप्त करने के बाद, यह परिणामी पेड़ के नोड्स के माध्यम से जाता है - प्रत्येक नोड में विशेषता संख्या और मूल्य इस पर तय किए जाते हैं, और इस विशेषता के लिए ऑब्जेक्ट की आने वाली विधि का उपयोग किस मूल्य पर निर्भर करता है, हम या तो सही वंशज या बाईं ओर जाते हैं, जब तक हम उस शीट पर नहीं पहुंचेंगे, जिसमें इस ऑब्जेक्ट के लिए एक उत्तर होगा।

predict विधि पिछली विधि के समान ही करती है, केवल वस्तुओं के समूह के लिए।

हम प्रसिद्ध कैलिफोर्निया घर डेटा सेट आयात करते हैं। यह डेटा के साथ एक नियमित डेटासेट है और प्रतिगमन समस्या को हल करने के लिए एक लक्ष्य है।

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) 

खैर, तुलना शुरू करते हैं! सबसे पहले, आइए देखें कि एल्गोरिथ्म कितनी तेजी से सीखता है। हमने स्केलेर में सेट किया है और खुद को केवल पैरामीटर max_depth , इसे 2 होने दें।

 %%time A = RegressionTree(2) #    A.fit(X,y) 

 from sklearn.tree import DecisionTreeRegressor %%time model = DecisionTreeRegressor(max_depth=2) #  Sklearn model.fit(X,y) 

निम्नलिखित प्रदर्शित किया जाएगा:

• हमारे एल्गोरिथ्म के लिए - सीपीयू समय: उपयोगकर्ता 4min 47s, sys: 8.25 एमएस, कुल: 4min 47s
  दीवार समय: 4min 47s
• Sklearn के लिए - सीपीयू समय: उपयोगकर्ता 53.5 एमएस, sys: 0 ns, कुल: 53.5 एमएस
  दीवार समय: 53.4 एमएस

जैसा कि आप देख सकते हैं, एल्गोरिथ्म हजारों बार धीमा सीखता है। क्या कारण है? चलो ठीक है।

याद रखें कि सबसे अच्छा विभाजन खोजने की प्रक्रिया कैसे व्यवस्थित है। जैसा कि आप जानते हैं, सामान्य तौर पर, जब वस्तुओं का आकार $$$एन$और संकेतों की संख्या के साथ $$$ड$सबसे अच्छा विभाजन खोजने की कठिनाई है $$$O (N * logN * d)$।

यह जटिलता कहां से आती है?

सबसे पहले, त्रुटि को प्रभावी ढंग से पुनर्गणना करने के लिए, विशेषता से गुजरने से पहले सबसे छोटे से सबसे बड़े तक जाने के लिए सभी स्तंभों को क्रमबद्ध करना आवश्यक है। जैसा कि हम प्रत्येक विशेषता के लिए करते हैं, यह एक संबंधित जटिलता बनाता है। जैसा कि आप देख सकते हैं, हम संकेतों को क्रमबद्ध करते हैं, लेकिन समस्या त्रुटि को mse में है - जब भी हम डेटा को mse विधि में mse , जो लाइन के लिए काम करता है। यह त्रुटि को इतना अयोग्य बनाता है! आखिरकार, एक विभाजन खोजने की कठिनाई बढ़ जाती है $$$O (N ^ 2 * d)$बड़े के लिए $$$एन$एल्गोरिथ्म को काफी धीमा कर देता है। इसलिए, हम अगले आइटम पर आसानी से आगे बढ़ते हैं।

2. रिग्रेशनट्री () तेज त्रुटि के साथ वर्ग

त्रुटि को जल्दी से ठीक करने के लिए क्या करने की आवश्यकता है? एक पेन और पेपर लें, और पेंट करें कि हमें कैसे सूत्र बदलना चाहिए।

मान लीजिए कि कुछ कदम पर पहले से ही एक त्रुटि की गणना है $$$एन$वस्तुओं। इसके निम्न सूत्र हैं: $$$\ sum_ {i = 1} ^ n (y_i - \ frac {\ _ sum_ {i = 1} ^ N y_i} {N}) ^ $$। यहां पर विभाजित करना आवश्यक है $$$एन$लेकिन अभी के लिए इसे छोड़ दें। हम जल्दी से इस त्रुटि को प्राप्त करना चाहते हैं - $$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ _ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ $$, अर्थात्, उस त्रुटि को फेंक दें जो तत्व का परिचय देता है $$$y_i$दूसरे भाग को।

चूंकि हम ऑब्जेक्ट को फेंकते हैं, इसलिए त्रुटि को दो स्थानों पर पुनरावृत्ति करना चाहिए - दाईं ओर (इस ऑब्जेक्ट को छोड़कर) और बाईं ओर (इस ऑब्जेक्ट को ध्यान में रखते हुए)। लेकिन सामान्यता के नुकसान के बिना हम केवल एक सूत्र को काटेंगे, क्योंकि वे समान होंगे।

चूंकि हम mse साथ काम करते हैं, इसलिए हम भाग्य से बाहर थे: एक त्रुटि के त्वरित mse को प्राप्त करना मुश्किल है, लेकिन जब अन्य मेट्रिक्स (उदाहरण के लिए, गिनी मानदंड, यदि हम वर्गीकरण समस्या को हल करते हैं) के साथ काम करते हैं, तो त्वरित रिकाउंट बहुत आसान है।

ठीक है, चलो सूत्र प्राप्त करना शुरू करें!

$$

$$\ sum_ {i = 1} ^ N (y_i - \ frac {\ _ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} (y_i -) \ frac {\ _ sum_ {i = 1} ^ N y_i} {N}) ^ 2 + (y_N - \ frac {\ sum_ {i = 1} ^ N y_i} {N}) ^ 2$$

हम पहले सदस्य को लिखेंगे:

$$

$$\ sum_ {i = 1} ^ {N-1} (y_i - \ frac {\ _ sum_ {i = 1} ^ N y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} }} (y_i - \ frac {\ _ sum_ {i = 1} ^ {N-1} y_i + y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (@ क्रेक) Ny_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_N} {N}) ^ 2 = \\ \ sum_ {i = 1} ^ {N-1} (\ _) frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} - \ frac {y_Ni - y_i} {N}) ^ 2 = \\ \ _ \ _ {i = 1] } ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - (\ frac {(N-1)) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} + (\ frac {y_N - y_i} {N} ^ 2 = \\ \ _) sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) ^ 2 - \ sum_ {= = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_N - y_i} {N} - (\ frac {y_Ni - y_i} {N}) ^ 2) = \\ \ sum_ {i = 1} ^ {N-1} (\ frac {(N-1) y_i - \ sum_ {i> 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) ^ 2 - \ sum_ {i = 1} ^ {N-1} (2 (\ frac) {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N}) \ frac {y_Ni - y_i} {N} - \\ - (\ frac {y_N - y_i}) एन}) ^ 2)$$

ऊ, बस थोड़ा सा बचा है। यह केवल आवश्यक राशि को व्यक्त करने के लिए बनी हुई है।

$$

$$\ sum_ {i = 1} ^ {N} (y_i - \ frac {\ _ sum_ {i = 1} ^ {N} y_i} {N}) ^ 2 = \ sum_ {i = 1} ^ {N-1} }} (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N-1}) ^ 2 * (\ frac {N-1} {N}) 2 - \\ \ sum_ {i = 1} ^ {N-1} (2 (\ frac {(N-1) y_i - \ sum_ {i = 1} ^ {N-1} y_i} {N} (\) frac {y_N - y_i} {N}) - (\ frac {y_Ni - y_i} {N}) ^ 2) + (y_N - \ sum_ {i = 1} ^ {N} \ frac {yi} {N}) ^ 2$$

और फिर यह स्पष्ट है कि वांछित राशि कैसे व्यक्त की जाए। त्रुटि को पुनर्गणना करने के लिए, हमें केवल दाएं और बाएं तत्वों के योग को संग्रहीत करने की आवश्यकता है, साथ ही नए तत्व, जो इनपुट पर पहुंचे। अब त्रुटि के लिए पुनरावर्ती है $$$O (1)$।

खैर, इसे कोड में लागू करते हैं।

 class RegressionTreeFastMse(): '''  RegressionTree    .        O(1). ''' #    def __init__(self, max_depth=3, min_size=10): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None #   -     def fit(self, X, y): #   -   y self.value = y.mean() #   - mse     (  # ,     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2 ,    -   #   - -    if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return self.left = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) # print ("    %d"%(self.max_depth - 1)) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

आइए अब उस समय को मापें जो अब प्रशिक्षण पर खर्च किया गया है, और स्केलेर से एनालॉग के साथ तुलना करें।

 %%time A = RegressionTreeFastMse(4, min_size=5) A.fit(X,y) test_mytree = A.predict(X) test_mytree 

 %%time model = DecisionTreeRegressor(max_depth=4) model.fit(X,y) test_sklearn = model.predict(X) 

• हमारे एल्गोरिथ्म के लिए, हम प्राप्त करते हैं - सीपीयू समय: उपयोगकर्ता 3.11 एस, एसआईएस: 2.7 एमएस, कुल: 3.11 एस
  दीवार समय: 3.11 एस।
• स्केलेरोन - सीपीयू समय से एल्गोरिथ्म के लिए: उपयोगकर्ता 45.9 एमएस, एसआईएस: 1.09 एमएस, कुल: 47 एमएस
  दीवार समय: 45.7 एमएस।

परिणाम पहले से अधिक सुखद हैं। ठीक है, चलो एल्गोरिथ्म में और सुधार करते हैं।

3. RegressionTree () सुविधाओं के रैखिक संयोजनों के साथ वर्ग

अब, हमारे एल्गोरिथ्म में, विशेषताओं के बीच संबंध किसी भी तरह से उपयोग नहीं किए जाते हैं। हम एक विशेषता को ठीक करते हैं और केवल अंतरिक्ष के ऑर्थोगोनल विभाजन को देखते हैं। विशेषताओं के बीच रैखिक संबंधों का उपयोग करना कैसे सीखें? यानी, सबसे अच्छे विभाजन की तलाश करना पसंद नहीं है $$$a_ {करतब} <x$, और $$$\ sum_ {i = 1} ^ K b_i * a_i <x$जहाँ $$$K$- हमारे अंतरिक्ष के आयाम से कुछ संख्या कम है?

कई विकल्प हैं, मैं अपने दृष्टिकोण से सबसे दिलचस्प में से दो को उजागर करूंगा। ये दोनों दृष्टिकोण फ्राइडमैन की पुस्तक में वर्णित हैं (उन्होंने इन पेड़ों का आविष्कार किया था)।

मैं एक तस्वीर दूंगा ताकि यह स्पष्ट हो सके कि क्या मतलब है:



सबसे पहले, आप इन रैखिक विभाजनों को एल्गोरिदम को खोजने की कोशिश कर सकते हैं। यह स्पष्ट है कि सभी रैखिक संयोजनों के माध्यम से छांटना असंभव है, क्योंकि अनंत संख्या में संयोजन होते हैं, इसलिए इस तरह के एक एल्गोरिथ्म लालची होना चाहिए, अर्थात, प्रत्येक पुनरावृत्ति पर, पिछले पुनरावृत्ति के परिणाम में सुधार होगा। इस एल्गोरिथ्म का मुख्य विचार पुस्तक में पढ़ा जा सकता है, मैं इस एल्गोरिथ्म के कार्यान्वयन के साथ अपने मित्र और सहकर्मियों के भंडार के लिए यहां एक लिंक भी छोड़ दूंगा।

दूसरे, अगर हम सबसे अच्छे ऑर्थोगोनल विभाजन को खोजने के विचार से दूर नहीं जाते हैं, तो हम डेटासेट को कैसे संशोधित करते हैं ताकि सुविधाओं के संबंध पर जानकारी का उपयोग किया जाए और खोज ऑर्थोगोनल विभाजन पर आधारित है? यह सही है, नए लोगों में मूल सुविधाओं के कुछ प्रकार के परिवर्तन करने के लिए। उदाहरण के लिए, आप सुविधाओं के कुछ संयोजन का योग ले सकते हैं और उनके द्वारा पहले से ही विभाजन की तलाश कर सकते हैं। इस तरह की एक विधि एल्गोरिथम अवधारणा में खराब होती है, लेकिन यह अपना काम करती है - यह कुछ प्रकार के गुणों में पहले से ही रूढ़िवादी विभाजन की खोज करती है।

ठीक है, इसे लागू करें - हम नई सुविधाओं के रूप में जोड़ देंगे, उदाहरण के लिए, सुविधा रकम के सभी प्रकार के संयोजन $$$i, j$जहाँ $$$I <j$। मैं ध्यान देता हूं कि इस मामले में एल्गोरिथ्म की जटिलता बढ़ जाएगी, यह स्पष्ट है कि कितनी बार। खैर, तेजी से विचार करने के लिए, हम साइथन का उपयोग करेंगे।

 %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeCython: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeCython left cpdef RegressionTreeCython right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.averages = averages self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def data_transform(self, np.ndarray[np.float64_t, ndim=2] X, list index_tuples): #   -       for i in index_tuples: #  ,       X = np.hstack((X, X[:, i[0]:(i[1]+1)].sum(axis=1).reshape(X.shape[0],1))) return X def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #        #  ,     if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(combinations(stuff,2)) #    X = self.data_transform(X, index_tuples) #   -   y self.value = y.mean() #   - mse     (  , #     )   base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -        delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue # 2    -   #   -      if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 # self.feature_idx -     . #   -  ,    -   #  ,   ,     #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeCython(self.max_depth - 1, averages=0) self.left.value = left_value self.right = RegressionTreeCython(self.max_depth - 1, averages=0) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): #   ,        if self.averages: stuff = list(range(0,X.shape[1],1)) index_tuples = list(itertools.combinations(stuff,2)) X = self.data_transform(X, index_tuples) y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

4. परिणामों की तुलना

खैर, परिणामों की तुलना करते हैं। हम एक ही पैरामीटर के साथ तीन एल्गोरिदम की तुलना करेंगे - स्केलेर का एक पेड़, हमारे साधारण पेड़ और नई सुविधाओं के साथ हमारा पेड़। हम अपने डेटासेट को कई बार प्रशिक्षण और परीक्षण सेट में विभाजित करेंगे, और त्रुटि की गणना करेंगे।

 from sklearn.model_selection import KFold def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in kf.split(X): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list 

अब सभी एल्गोरिदम चलाते हैं।

 import matplotlib.pyplot as plt data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_sklearn_tree = get_metrics(X,y,30,DecisionTreeRegressor(max_depth=4, min_samples_leaf=10)) er_fast_mse_tree = get_metrics(X,y,30,RegressionTreeFastMse(4, min_size=10)) er_averages_tree = get_metrics(X,y,30,RegressionTreeCython(4, min_size=10)) %matplotlib inline data = [er_sklearn_tree, er_fast_mse_tree, er_averages_tree] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Tree', 'Fast Mse Tree', 'Averages Tree']) plt.grid() plt.show() 

परिणाम:



Sklearn से हमारा नियमित पेड़ खो गया (जो समझ में आता है: Sklearn अच्छी तरह से अनुकूलित है, और डिफ़ॉल्ट रूप से पेड़ में अभी भी बहुत सारे पैरामीटर हैं जिन्हें हम ध्यान में नहीं रखते हैं), लेकिन मात्राओं को जोड़ते समय, परिणाम अधिक सुखद हो जाता है।

संक्षेप में: हमने सीखा कि स्क्रैच से निर्णायक पेड़ों को कैसे लिखना है, अपने प्रदर्शन को बेहतर बनाने के तरीके सीखे और स्केलेर से एल्गोरिदम के साथ तुलना करके वास्तविक डेटासेट पर उनकी प्रभावशीलता का परीक्षण किया। हालांकि, यहां प्रस्तुत तरीके एल्गोरिदम के सुधार को सीमित नहीं करते हैं, इसलिए ध्यान रखें कि प्रस्तावित कोड को और भी बेहतर बनाया जा सकता है। अगले लेख में, हम इन एल्गोरिदम के आधार पर बूस्टिंग लिखेंगे।

सभी सफलता!