स्क्रैच से XGBoost लिखना - भाग 2: ग्रेडिंग बूस्टिंग

सभी को नमस्कार!

पिछले लेख में, हमने यह पता लगाया कि कैसे निर्णय पेड़ों की व्यवस्था की जाती है, और खरोंच से हमने लागू किया
निर्माण एल्गोरिथ्म, एक साथ अनुकूलन और इसे सुधारना। इस लेख में, हम ग्रेडिंग बूस्टिंग एल्गोरिदम को लागू करेंगे और अंत में हम अपना खुद का एक्सजीओओस्ट बनाएंगे। कथन एक ही पैटर्न का अनुसरण करेगा: हम एक एल्गोरिथ्म लिखते हैं, इसका वर्णन करते हैं, स्केलेर से एनालॉग्स के साथ काम करने के परिणामों की तुलना करके इसे संक्षेप में प्रस्तुत करते हैं।

इस अनुच्छेद में, कोड में कार्यान्वयन पर भी जोर दिया जाएगा, इसलिए पूरे सिद्धांत को एक साथ (उदाहरण के लिए, ओडीएस पाठ्यक्रम में ) पढ़ना बेहतर है, और पहले से ही सिद्धांत के ज्ञान के साथ, आप इस लेख पर आगे बढ़ सकते हैं, क्योंकि विषय बल्कि जटिल है।



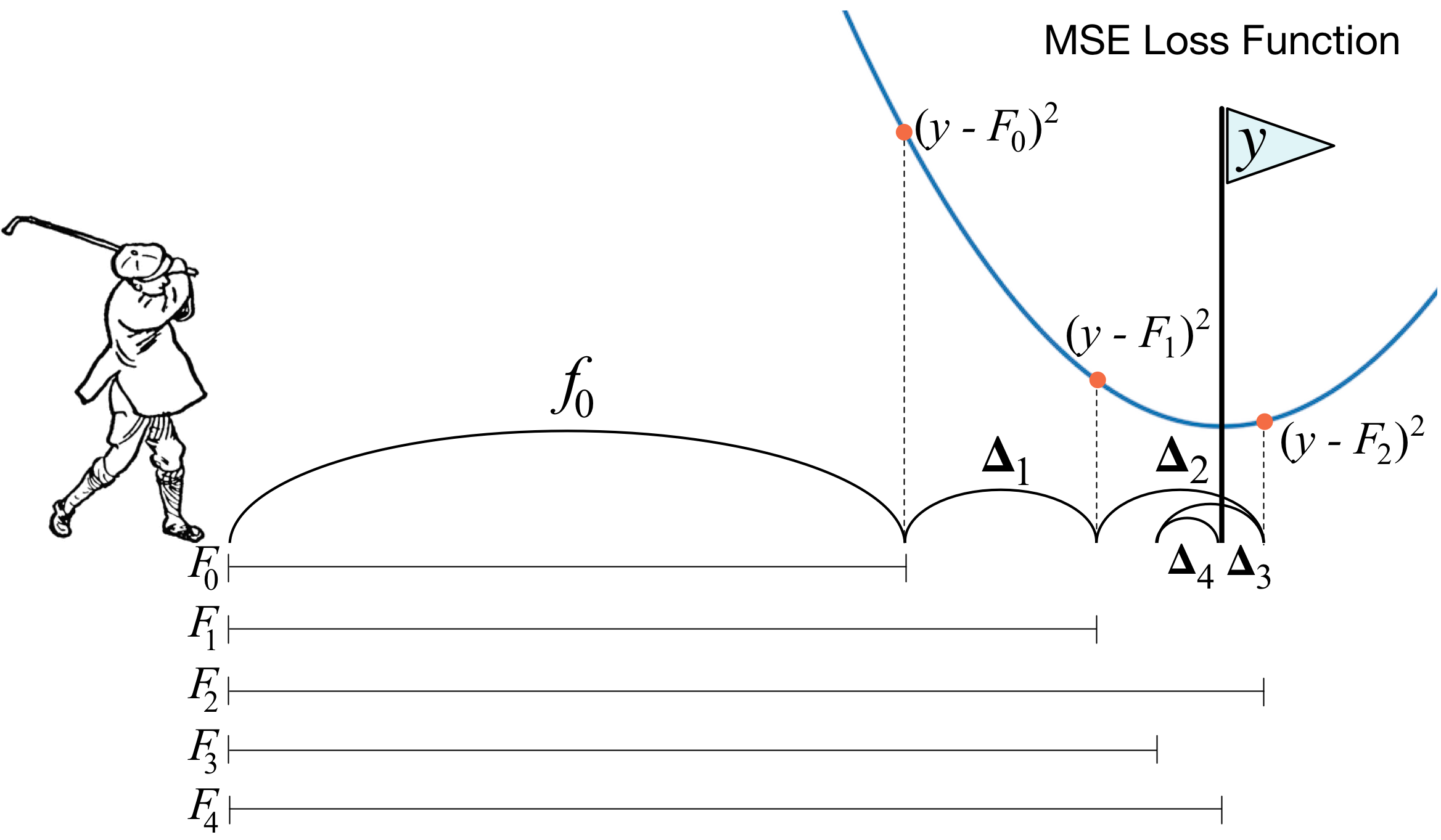
ग्रेडिएंट बूस्टिंग क्या है? एक गोल्फर की एक तस्वीर मुख्य विचार का पूरी तरह से वर्णन करती है। छेद में गेंद को चलाने के लिए, गोल्फर हर अगले हिट को पिछले स्ट्रोक के अनुभव को ध्यान में रखता है - उसके लिए गेंद को छेद में डालने के लिए यह एक आवश्यक शर्त है। यदि यह बहुत अशिष्ट है (मैं गोल्फ का मास्टर नहीं हूं :)), तो प्रत्येक नई हिट के साथ पहली चीज जिस पर एक गोल्फ खिलाड़ी दिखता है वह पिछली हिट के बाद गेंद और छेद के बीच की दूरी है। और मुख्य कार्य अगले झटका के साथ इस दूरी को कम करना है।

बूस्टिंग बहुत ही समान तरीके से बनाया गया है। सबसे पहले, हमें "होल" की परिभाषा को पेश करने की आवश्यकता है, अर्थात्, वह लक्ष्य जिसके लिए हम प्रयास करेंगे। दूसरे, हमें यह समझने की ज़रूरत है कि लक्ष्य के करीब जाने के लिए हमें किस पक्ष के साथ एक क्लब को हरा देना चाहिए। तीसरा, इन सभी नियमों को ध्यान में रखते हुए, आपको स्ट्रोक के सही अनुक्रम के साथ आने की आवश्यकता है ताकि प्रत्येक बाद में गेंद और छेद के बीच की दूरी कम हो जाए।

अब हम थोड़ी और कठोर परिभाषा देते हैं। हम भारित मतदान के मॉडल का परिचय देते हैं:

$$

$$h (x) = \ sum_ {i = 1} ^ nb_ia_i, x \ _ in X, b_i \ _ R$$

यहां $$$X$ वह स्थान है जहाँ से हम वस्तुओं को लेते हैं, $$$b_i, a_i$ - यह मॉडल और मॉडल के सामने गुणांक है, अर्थात् निर्णय वृक्ष है। मान लीजिए कि पहले से ही कुछ चरणों में, वर्णित नियमों का उपयोग करके, रचना में जोड़ना संभव था $$$T-1$ कमजोर एल्गोरिथ्म। यह समझने के लिए कि किस तरह का एल्गोरिदम स्टेप में होना चाहिए $$$T$ , हम त्रुटि फ़ंक्शन का परिचय देते हैं:

$$$त्रुटी (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) \ rightarna min_ {a_T, b_T}$

यह पता चलता है कि सबसे अच्छा एल्गोरिथ्म वह होगा जो पिछले पुनरावृत्तियों में प्राप्त त्रुटि को कम कर सकता है। और चूंकि बूस्टिंग ग्रैडिएंट है, तो इस त्रुटि फ़ंक्शन के लिए आवश्यक रूप से एक एंटीग्रैडिएंट वेक्टर होना चाहिए जिसके साथ आप न्यूनतम की तलाश में आगे बढ़ सकते हैं। वह सब है!

कार्यान्वयन से तुरंत पहले, मैं कुछ शब्द जोड़ूंगा कि हमारे साथ सब कुछ कैसे व्यवस्थित होगा। पिछले लेख में, हम MSE को नुकसान के रूप में लेते हैं। आइए इसकी ढाल की गणना करें:

$$

$$mse (y, भविष्यवाणी) = (y - भविष्यवाणी) ^ 2 \\ \ nabla_ {भविष्यवाणी} mse (y, भविष्यवाणी) = भविष्यवाणी - y$$

इस प्रकार, एंटीग्रैडिएंट वेक्टर के बराबर होगा $$$य - भविष्यवाणी$ । कदम पर $$$मैं$ हम पिछले पुनरावृत्तियों में प्राप्त एल्गोरिथ्म की त्रुटियों पर विचार करते हैं। इसके बाद, हम इन त्रुटियों पर हमारे नए एल्गोरिथ्म को प्रशिक्षित करते हैं, और फिर इसे एक माइनस साइन और कुछ गुणांक के साथ हमारे पहनावा में जोड़ते हैं।

अब शुरू करते हैं।

1. सामान्य ग्रेडिंग बूस्टिंग क्लास का कार्यान्वयन

import pandas as pd import matplotlib.pyplot as plt import numpy as np from tqdm import tqdm_notebook from sklearn import datasets from sklearn.metrics import mean_squared_error as mse from sklearn.tree import DecisionTreeRegressor import itertools %matplotlib inline %load_ext Cython %%cython -a import itertools import numpy as np cimport numpy as np from itertools import * cdef class RegressionTreeFastMse: cdef public int max_depth cdef public int feature_idx cdef public int min_size cdef public int averages cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef RegressionTreeFastMse left cpdef RegressionTreeFastMse right def __init__(self, max_depth=3, min_size=4, averages=1): self.max_depth = max_depth self.min_size = min_size self.value = 0 self.feature_idx = -1 self.feature_threshold = 0 self.left = None self.right = None def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef np.float64_t mean1 = 0.0 cpdef np.float64_t mean2 = 0.0 cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef np.float64_t delta1 = 0.0 cpdef np.float64_t delta2 = 0.0 cpdef np.float64_t sm1 = 0.0 cpdef np.float64_t sm2 = 0.0 cpdef list index_tuples cpdef list stuff cpdef long idx = 0 cpdef np.float64_t prev_error1 = 0.0 cpdef np.float64_t prev_error2 = 0.0 cpdef long thres = 0 cpdef np.float64_t error = 0.0 cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 #   -   y self.value = y.mean() #   - mse     base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 #     if self.max_depth <= 1: return dim_shape = X.shape[1] left_value, right_value = 0, 0 for feat in range(dim_shape): prev_error1, prev_error2 = base_error, 0 idxs = np.argsort(X[:, feat]) #      mean1, mean2 = y.mean(), 0 sm1, sm2 = y.sum(), 0 N = X.shape[0] N1, N2 = N, 0 thres = 1 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] #   -  ,  ,    delta1 = (sm1 - y[idx]) * 1.0 / N1 - mean1 delta2 = (sm2 + y[idx]) * 1.0 / N2 - mean2 #   sm1 -= y[idx] sm2 += y[idx] #    O(1) prev_error1 += (delta1**2) * N1 prev_error1 -= (y[idx] - mean1)**2 prev_error1 -= 2 * delta1 * (sm1 - mean1 * N1) mean1 = sm1/N1 prev_error2 += (delta2**2) * N2 prev_error2 += (y[idx] - mean2)**2 prev_error2 -= 2 * delta2 * (sm2 - mean2 * N2) mean2 = sm2/N2 #       if thres < N - 1 and np.abs(x - X[idxs[thres + 1], feat]) < 1e-5: thres += 1 continue if (prev_error1 + prev_error2 < error): if (min(N1,N2) > self.min_size): #         self.feature_idx, self.feature_threshold = feat, x #     left_value, right_value = mean1, mean2 #  -     flag = 1 error = prev_error1 + prev_error2 thres += 1 #   ,  if self.feature_idx == -1: return #    self.left = RegressionTreeFastMse(self.max_depth - 1) self.left.value = left_value self.right = RegressionTreeFastMse(self.max_depth - 1) self.right.value = right_value #      idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) #   self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.1, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree def fit(self, X, y): self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: #    resid = (y - prediction) #    if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth, min_size = self.min_size) if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth, min_size = self.min_size) #     tree.fit(X, resid) #        b = tree.predict(X).reshape([X.shape[0]]) self.trees_.append(tree) prediction += self.learning_rate * b #       if t > 0: self.loss_by_iter.append(mse(y,prediction)) return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

अब हम यह सुनिश्चित करने के लिए प्रशिक्षण सेट पर हानि वक्र का निर्माण करेंगे कि प्रत्येक पुनरावृत्ति पर हमारे पास वास्तव में कमी है।

 GDB = GradientBoosting(n_estimators=50) GDB.fit(X,y) x = GDB.predict(X) plt.grid() plt.title('Loss by iterations') plt.plot(GDB.loss_by_iter) 

2. निर्णायक पेड़ों पर बाग लगाना

ठीक है, इससे पहले कि हम परिणामों की तुलना करें, चलो पेड़ों पर बैग लगाने की प्रक्रिया के बारे में बात करते हैं।

यहां सब कुछ सरल है: हम खुद को फिर से संवारने से बचाना चाहते हैं, और इसलिए, वापसी के साथ नमूने की मदद से, हम अपनी भविष्यवाणियों को औसत करेंगे ताकि गलती से आउटलेयर में न चला जाए (यह इस तरह काम क्यों करता है, लिंक को बेहतर पढ़ें)।

 class Bagging(): '''  Bagging -      . ''' def __init__(self, max_depth = 3, min_size=10, n_samples = 10): #super(CART, self).__init__() self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeFastMse(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): #      indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): #    self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): #        num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

खैर, अब एक बुनियादी एल्गोरिथ्म के रूप में हम एक पेड़ का उपयोग नहीं कर सकते हैं, लेकिन पेड़ों से बैगिंग कर सकते हैं - इसलिए फिर से, हम खुद को फिर से संवारने से बचाएंगे।

3. परिणाम

हमारे एल्गोरिदम के परिणामों की तुलना करें।

 from sklearn.model_selection import KFold import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn import copy def get_metrics(X,y,n_folds=2, model=None): kf = KFold(n_splits=n_folds, shuffle=True) kf.get_n_splits(X) er_list = [] for train_index, test_index in tqdm_notebook(kf.split(X)): X_train, X_test = X[train_index], X[test_index] y_train, y_test = y[train_index], y[test_index] model.fit(X_train,y_train) predict = model.predict(X_test) er_list.append(mse(y_test, predict)) return er_list data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) er_boosting = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Tree' )) er_boobagg = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=40, base_tree='Bagging' )) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=40, learning_rate=0.1)) %matplotlib inline data = [er_sklearn_boosting, er_boosting, er_boobagg] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['Sklearn Boosting', 'Boosting', 'BooBag']) plt.grid() plt.show() 

हम प्राप्त किया:



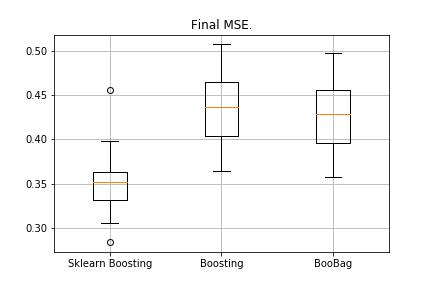
हम अभी तक स्केलेर से एनालॉग को नहीं हरा सकते हैं, क्योंकि फिर से हम इस पद्धति में उपयोग किए जाने वाले बहुत सारे मापदंडों को ध्यान में नहीं रखते हैं। हालाँकि, हम देखते हैं कि बैगिंग से थोड़ी मदद मिलती है।

आइए निराशा न करें, और XGBoost लिखने के लिए आगे बढ़ें।

4. XGBoost

आगे पढ़ने से पहले, मैं आपको अगले वीडियो के साथ खुद को परिचित करने की दृढ़ता से सलाह देता हूं, जो सिद्धांत को बहुत अच्छी तरह से समझाता है।

याद रखें कि सामान्य वृद्धि में हम किस त्रुटि को कम करते हैं:

$$

$$गलत (h) = \ sum_ {j = 1} ^ N L (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j))$$

XGBoost स्पष्ट रूप से इस त्रुटि कार्यक्षमता में नियमितीकरण जोड़ता है:

$$

$$इर (h) = \ sum_ {j = 1} ^ NL (\ sum_ {i = 1} ^ {T-1} a_ib_i (x_j) + b_Ta_T (x_j)) + \ sum_ / i = 1} ^ T \ ओमेगा (a_i)$$

इस कार्यक्षमता पर विचार कैसे करें? पहले, हम इसे दूसरे क्रम की टेलर सीरीज़ की मदद से अनुमानित करते हैं, जहाँ नए एल्गोरिथ्म को एक वृद्धि के रूप में माना जाता है जिसके साथ हम आगे बढ़ेंगे, और फिर हम पहले से ही इस बात पर निर्भर करते हैं कि हमें किस तरह का नुकसान हुआ है:

$$$f (x + \ delta x) \ thickapprox f (x) + f (x) '\ delta x + 0.5 * f (x)' '(\ delta x) ^ 2$

यह निर्धारित करना आवश्यक है कि हम किस पेड़ को बुरा मानेंगे और कौन सा अच्छा है।

क्या सिद्धांत प्रतिगमन के साथ बनाया गया है पर स्मरण करो $$$L_2$ -अतिक्रमण - रिग्रेशन से पहले गुणांक के मूल्य जितना अधिक सामान्य होते हैं, उतना ही, इसलिए, उन्हें यथासंभव छोटा होना चाहिए।

XGBoost में, विचार बहुत समान है: एक पेड़ पर जुर्माना लगाया जाता है यदि उसमें पत्तियों में मूल्यों के मानदंड का योग बहुत बड़ा है। इसलिए, पेड़ की जटिलता निम्नानुसार पेश की गई है:

$$

$$\ omega (a) = \ gamma Z + 0.5 * \ sum_ {i = 1} ^ {Z} w_i ^ 2$$

$$$w$ - पत्तियों में मान, $$$Z$ - पत्तियों की संख्या।

वीडियो में संक्रमण सूत्र हैं, हमने उन्हें यहां प्रदर्शित नहीं किया है। यह सब इस तथ्य पर उतरता है कि हम एक नया विभाजन चुनेंगे, अधिकतम लाभ प्राप्त करेंगे:

$$

$$Gain = \ frac {G_l ^ 2} {S_l ^ 2 + \ _ lambda} + \ frac {G_r ^ 2} {S_r ^ 2 + \ lambda} - \ frac {(Gl + G_r) ^ 2} {S_l ^ 2 + S_r ^ 2 + \ lambda} - \ Gamma$$

यहां $$$गामा, \ lambda$ नियमितीकरण के संख्यात्मक मानदंड हैं, और $$$G_i, S_i$ - इस विभाजन के लिए पहले और दूसरे डेरिवेटिव की संगत रकम।

यही है, सिद्धांत बहुत संक्षेप में कहा गया है, लिंक दिए गए हैं, अब बात करते हैं कि यदि हम एमएसई के साथ काम करते हैं तो डेरिवेटिव क्या होगा। यह सरल है:

$$$mse (y, भविष्यवाणी) = (y - भविष्यवाणी) ^ 2 \\ \ nabla_ {भविष्यवाणी} mse (y, भविष्यवाणी) = भविष्यवाणी - y \\ \ nabla_ {भविष्यवाणी} ^ 2 mse (y, भविष्यवाणी) - 1$

हम राशि की गणना कब करेंगे $$$G_i, S_i$ , बस पहले में जोड़ें $$$भविष्यवाणी - y$ और दूसरा सिर्फ मात्रा है।

 %%cython -a import numpy as np cimport numpy as np cdef class RegressionTreeGain: cdef public int max_depth cdef public np.float64_t gain cdef public np.float64_t lmd cdef public np.float64_t gmm cdef public int feature_idx cdef public int min_size cdef public np.float64_t feature_threshold cdef public np.float64_t value cpdef public RegressionTreeGain left cpdef public RegressionTreeGain right def __init__(self, int max_depth=3, np.float64_t lmd=1.0, np.float64_t gmm=0.1, min_size=5): self.max_depth = max_depth self.gmm = gmm self.lmd = lmd self.left = None self.right = None self.feature_idx = -1 self.feature_threshold = 0 self.value = -1e9 self.min_size = min_size return def fit(self, np.ndarray[np.float64_t, ndim=2] X, np.ndarray[np.float64_t, ndim=1] y): cpdef long N = X.shape[0] cpdef long N1 = X.shape[0] cpdef long N2 = 0 cpdef long idx = 0 cpdef long thres = 0 cpdef np.float64_t gl, gr, gn cpdef np.ndarray[long, ndim=1] idxs cpdef np.float64_t x = 0.0 cpdef np.float64_t best_gain = -self.gmm if self.value == -1e9: self.value = y.mean() base_error = ((y - self.value) ** 2).sum() error = base_error flag = 0 if self.max_depth <= 1: return dim_shape = X.shape[1] left_value = 0 right_value = 0 #    # -  -   mse, L = (y - pred)**2 # dL/dpred = pred - y,          - # dL^2/d^2pred = 1 - ,       for feat in range(dim_shape): idxs = np.argsort(X[:, feat]) gl,gr = y.sum(),0.0 N1, N2, thres = N, 0, 0 while thres < N - 1: N1 -= 1 N2 += 1 idx = idxs[thres] x = X[idx, feat] gl -= y[idx] gr += y[idx] #   gn = (gl**2) / (N1 + self.lmd) + (gr**2) / (N2 + self.lmd) gn -= ((gl + gr)**2) / (N1 + N2 + self.lmd) + self.gmm if thres < N - 1 and x == X[idxs[thres + 1], feat]: thres += 1 continue #     if (gn > best_gain) and (min(N1,N2) > self.min_size): flag = 1 best_gain = gn left_value = -gl / (N1 + self.lmd) right_value = -gr / (N2 + self.lmd) self.feature_idx = feat self.feature_threshold = x thres += 1 self.gain = best_gain if self.feature_idx == -1: return self.left = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.left.value = left_value self.right = RegressionTreeGain(max_depth=self.max_depth - 1, gmm=self.gmm, lmd=self.lmd) self.right.value = right_value idxs_l = (X[:, self.feature_idx] > self.feature_threshold) idxs_r = (X[:, self.feature_idx] <= self.feature_threshold) self.left.fit(X[idxs_l, :], y[idxs_l]) self.right.fit(X[idxs_r, :], y[idxs_r]) #    if (self.left.left == None or self.right.left == None): if self.gain < 0.0: self.left = None self.right = None self.feature_idx = -1 def __predict(self, np.ndarray[np.float64_t, ndim=1] x): if self.feature_idx == -1: return self.value if x[self.feature_idx] > self.feature_threshold: return self.left.__predict(x) else: return self.right.__predict(x) def predict(self, np.ndarray[np.float64_t, ndim=2] X): y = np.zeros(X.shape[0]) for i in range(X.shape[0]): y[i] = self.__predict(X[i]) return y 

एक छोटा स्पष्टीकरण: अधिक सुंदर लाभ के साथ पेड़ों में सूत्र बनाने के लिए, बढ़ावा देने के लिए हम एक ऋण चिह्न के साथ लक्ष्य को प्रशिक्षित करते हैं।

हम अपने बूस्टिंग को थोड़ा संशोधित करते हैं, कुछ मापदंडों को अनुकूल बनाते हैं। उदाहरण के लिए, यदि हम देखते हैं कि नुकसान एक पठार तक पहुंचना शुरू हो गया है, तो हम सीखने की दर को कम करते हैं और निम्नलिखित अनुमान लगाने वालों के लिए अधिकतम_दोपहर बढ़ाते हैं। हम एक नया बैगिंग भी जोड़ेंगे - अब हम लाभ के साथ ट्री बैगिंग्स पर बढ़ावा देंगे:

 class Bagging(): def __init__(self, max_depth = 3, min_size=5, n_samples = 10): self.max_depth = max_depth self.min_size = min_size self.n_samples = n_samples self.subsample_size = None self.list_of_Carts = [RegressionTreeGain(max_depth=self.max_depth, min_size=self.min_size) for _ in range(self.n_samples)] def get_bootstrap_samples(self, data_train, y_train): indices = np.random.randint(0, len(data_train), (self.n_samples, self.subsample_size)) samples_train = data_train[indices] samples_y = y_train[indices] return samples_train, samples_y def fit(self, data_train, y_train): self.subsample_size = int(data_train.shape[0]) samples_train, samples_y = self.get_bootstrap_samples(data_train, y_train) for i in range(self.n_samples): self.list_of_Carts[i].fit(samples_train[i], samples_y[i].reshape(-1)) return self def predict(self, test_data): num_samples = test_data.shape[0] pred = [] for i in range(self.n_samples): pred.append(self.list_of_Carts[i].predict(test_data)) pred = np.array(pred).T return np.array([np.mean(pred[i]) for i in range(num_samples)]) 

 class GradientBoosting(): def __init__(self, n_estimators=100, learning_rate=0.2, max_depth=3, random_state=17, n_samples = 15, min_size = 5, base_tree='Bagging'): self.n_estimators = n_estimators self.max_depth = max_depth self.learning_rate = learning_rate self.initialization = lambda y: np.mean(y) * np.ones([y.shape[0]]) self.min_size = min_size self.loss_by_iter = [] self.trees_ = [] self.loss_by_iter_test = [] self.n_samples = n_samples self.base_tree = base_tree #  -       #   ,   lr   max_depth self.add_to_max_depth = 1 self.init_mse_board = 1.5 def fit(self, X, y): print (self.base_tree) self.X = X self.y = y b = self.initialization(y) prediction = b.copy() for t in tqdm_notebook(range(self.n_estimators)): if t == 0: resid = y else: resid = (y - prediction) if (mse(temp_resid,resid) < self.init_mse_board): self.init_mse_board /= 1.5 self.add_to_max_depth += 1 self.learning_rate /= 1.1 # print ('Alert!', t, self.add_to_max_depth) if self.base_tree == 'Bagging': tree = Bagging(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid if self.base_tree == 'Tree': tree = RegressionTreeFastMse(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) if self.base_tree == 'XGBoost': tree = RegressionTreeGain(max_depth=self.max_depth+self.add_to_max_depth, min_size = self.min_size) resid = -resid tree.fit(X, resid) b = tree.predict(X).reshape([X.shape[0]]) # print (b.shape) self.trees_.append(tree) prediction += self.learning_rate * b temp_resid = resid return self def predict(self, X): #   –          pred = np.ones([X.shape[0]]) * np.mean(self.y) #    for t in range(self.n_estimators): pred += self.learning_rate * self.trees_[t].predict(X).reshape([X.shape[0]]) return pred 

5. परिणाम

परंपरा से, हम परिणामों की तुलना करते हैं:

 data = datasets.fetch_california_housing() X = np.array(data.data) y = np.array(data.target) import matplotlib.pyplot as plt from sklearn.ensemble import GradientBoostingRegressor as GDBSklearn er_boosting_bagging = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='Bagging')) er_boosting_xgb = get_metrics(X,y,30,GradientBoosting(max_depth=3, n_estimators=150,base_tree='XGBoost')) er_sklearn_boosting = get_metrics(X,y,30,GDBSklearn(max_depth=3,n_estimators=150,learning_rate=0.2)) %matplotlib inline data = [er_sklearn_boosting, er_boosting_xgb, er_boosting_bagging] fig7, ax7 = plt.subplots() ax7.set_title('') ax7.boxplot(data, labels=['GdbSklearn', 'Xgboost', 'XGBooBag']) plt.grid() plt.show() 

चित्र इस प्रकार होगा:



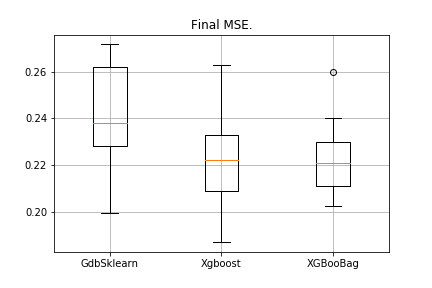
XGBoost में सबसे कम त्रुटि है, लेकिन XGBooBag में अधिक भीड़-भाड़ वाली त्रुटि है, जो निश्चित रूप से बेहतर है: एल्गोरिथ्म अधिक स्थिर है।

वह सब है। मैं वास्तव में आशा करता हूं कि दो लेखों में प्रस्तुत सामग्री उपयोगी थी, और आप अपने लिए कुछ नया सीख सकते थे। मैं सलाह के लिए एंटोन को व्यापक प्रतिक्रिया और स्रोत कोड, और अध्ययन के लिए कठिन कार्य के लिए व्लादिमीर के लिए दिमित्री के लिए विशेष आभार व्यक्त करता हूं।

सभी सफलता!