पेजरैंक कैसे काम करता है: रैखिक बीजगणित और विद्युत विधि के माध्यम से आर में कार्यान्वयन

हैलो, हब्रोस्क नागरिकों!

मेरा नाम एलेक्स है। इस बार मैंने ITAR-TASS में कार्यस्थल से प्रसारण किया।

इस लघु पाठ में, मैं आपको R भाषा में सरल, समझ में आने वाले उदाहरणों का उपयोग करके पेजरैंक © (इसके बाद मैं इसे पीआर कहूंगा) की गणना करने की विधि से परिचित कराऊंगा। एल्गोरिथ्म Google की एक बौद्धिक संपदा है, लेकिन, डेटा विश्लेषण कार्यों के लिए इसकी उपयोगिता के कारण, कई कार्यों का उपयोग किया जाता है। , जिसे ग्राफ में बड़े नोड्स की खोज करने और उन्हें महत्व देकर रैंकिंग में कमी की जा सकती है।

किसी बड़ी कंपनी का किसी पोस्ट में उल्लेख करना विज्ञापन नहीं है।

चूँकि मैं एक पेशेवर गणितज्ञ नहीं हूँ, इसलिए मैं इस लेख और इस ट्यूटोरियल को एक मार्गदर्शक के रूप में उपयोग करता हूँ - और आपको सलाह देता हूँ।

पीआर की सहज समझ

यह समझना कि यह कैसे काम करता है मुश्किल नहीं है। तत्वों का एक समूह होता है जो परस्पर जुड़े होते हैं। यहां बताया गया है कि वे कैसे जुड़े हुए हैं - यह एक व्यापक प्रश्न है: शायद लिंक के माध्यम से (जैसे Google), शायद एक-दूसरे के संदर्भ (लगभग समान लिंक) के माध्यम से, तत्वों (मार्कोव प्रक्रिया के मैट्रिक्स) के बीच संक्रमण की संभावनाएं भौतिक को निर्दिष्ट किए बिना एक प्राथमिकता हो सकती हैं। संचार का अर्थ। मैं इन तत्वों को महत्व का एक निश्चित मानदंड सौंपना चाहूंगा, जो इस संभावना के बारे में जानकारी लेगा कि इस तत्व को प्रसार प्रक्रिया में ग्राफ के माध्यम से यात्रा करने वाले कुछ अमूर्त कण द्वारा दौरा किया जाएगा।

उम, यह बहुत स्पष्ट नहीं लगता है। एक खसखस के साथ एक लैपटॉप का उपयोग करके एक आदमी की कल्पना करना आसान है, खोज परिणामों के पृष्ठों को सर्फ करना, एक हुक्का धूम्रपान करना, एक पृष्ठ से दूसरे पृष्ठ के लिंक के बाद और अधिक से अधिक बार एक ही पृष्ठ (या पृष्ठ) पर दिखाई देते हैं।

यह इस तथ्य के कारण है कि उनके द्वारा देखे गए कुछ पृष्ठ मूल स्रोत में ऐसी रोचक जानकारी रखते हैं कि अन्य पृष्ठ लिंक के संकेत के साथ इसे पुन: छापने के लिए मजबूर हो जाते हैं।

Google में ऐसे व्यक्ति का नाम रैंडम सर्फर था। वह प्रसार की प्रक्रिया में एक कण है: समय के साथ ग्राफ पर स्थिति का एक असतत परिवर्तन। और वह संभावना जिसके साथ वह पृष्ठ पर जाता है एक प्रसार समय के साथ अनंत तक जाता है पीआर।

पीआर गणना का सरल कार्यान्वयन

आइए सहमत हैं - हम 10 तत्वों के साथ काम करते हैं, ऐसे छोटे, आरामदायक छोटे ग्राफ में।

# clear environment rm(list = ls()); gc() ## load libs library(data.table) library(magrittr) library(markovchain) ## dummy data number_nodes <- 10 node_names <- letters[seq_len(number_nodes)] set.seed(1) nodes <- sapply( seq_len(number_nodes), function(x) { paste( c( node_names[-x] , sample(node_names[-x], sample(1:5, 1), replace = T) ) , collapse = ' ' ) } ) names(nodes) <- node_names print( paste(nodes, collapse = '; ') ) ## make long dt dt <- data.table( citing_node = node_names , cited_node = nodes ) %>% .[, .(cited_node = unlist(strsplit(cited_node, ' '))), by = citing_node] %>% dcast( . , cited_node ~ citing_node , fun.aggregate = length ) dt apply(dt[,-1,with=F], 2, sum) ## affinity matrix A <- as.matrix(dt[, 2:dim(dt)[2]]) A <- sweep(A, 2, colSums(A), `/`) A[is.nan(A)] <- 0 rowSums(A) colSums(A) mark <- new("markovchain", transitionMatrix = t(A), states = node_names, name = "mark") plot(mark) 

10 तत्वों में से प्रत्येक (नोड्स) में यादृच्छिक क्रम में अन्य नोड्स के 10 से 14 संदर्भ शामिल हैं, खुद को छोड़कर। फिलहाल, हम केवल यह तय करते हैं कि उल्लिखित डेटा एक वेब लिंक है।

यह स्पष्ट है कि ऐसा हो सकता है कि कुछ तत्व दूसरों की तुलना में अधिक बार उल्लिखित हों। इसे देखें।

वैसे, मैं प्रयोगों के लिए data.table पैकेज का उपयोग करने की सलाह देता हूं। Tidyverse के सिद्धांतों के साथ संयोजन में, सब कुछ कुशलतापूर्वक और जल्दी से निकलता है।

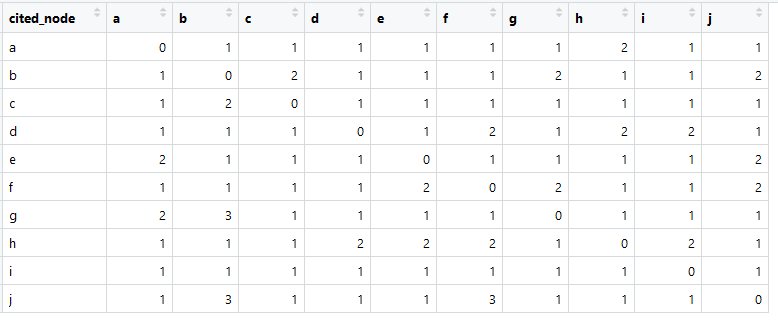
इस तरह से हमारा लिंक मैट्रिक्स दिखता है (अंग्रेजी में इसे अक्सर आसन्न मैट्रिक्स कहा जाता है)।

प्रत्येक स्तंभ में योग शून्य से अधिक है, जिसका अर्थ है कि प्रत्येक तत्व का किसी अन्य तत्व के साथ संबंध है (यह आगे के विश्लेषण के लिए महत्वपूर्ण है)।

> लागू करें (डीटी [, - 1, साथ = एफ], 2, योग)
abcdefghij
11 14 10 10 11 13 11 11 11 12

इस तालिका के आधार पर, हम तथाकथित एफ़िनिटी मैट्रिक्स बना सकते हैं, या, हमारी राय में, निकटता मैट्रिक्स (और इसे संक्रमण मैट्रिक्स भी कहा जाता है), जिसे गणितज्ञ स्टोकेस्टिक मैट्रिक्स (स्तंभ-स्टोकेस्टिक मैट्रिक्स) कहते हैं: मुख्य स्रोत

इसे A नाम के एक वेरिएबल को असाइन करें।



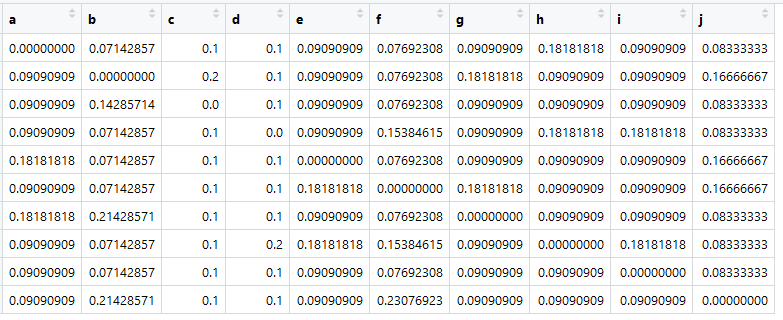
अब सबसे महत्वपूर्ण बात यह है कि सभी स्तंभों में योग एक के बराबर है।

> colSums (ए)
abcdefghij
1 1 1 1 1 1 1 1 1 1

यहाँ यह है - संक्रमण का एक मैट्रिक्स, यह मार्कोव है, यह समानता है। एक कॉलम में एक तत्व से एक पंक्ति में एक तत्व के लिए संक्रमण की संभावनाएं हैं।

ये, निश्चित रूप से, "समानताएं" वास्तविक नहीं हैं। उदाहरण के लिए, उदाहरण के लिए, यदि हम दस्तावेजों की प्रस्तुति के बीच कोण के कोसाइन की गणना करेंगे। लेकिन यह महत्वपूर्ण है कि संक्रमण मैट्रिक्स को (छद्म) संभावनाओं के लिए कम कर दिया जाए ताकि प्रत्येक स्तंभ पर योग एक के बराबर हो।

चलो मार्कोव संक्रमण ग्राफ (हमारे ए) को देखें:



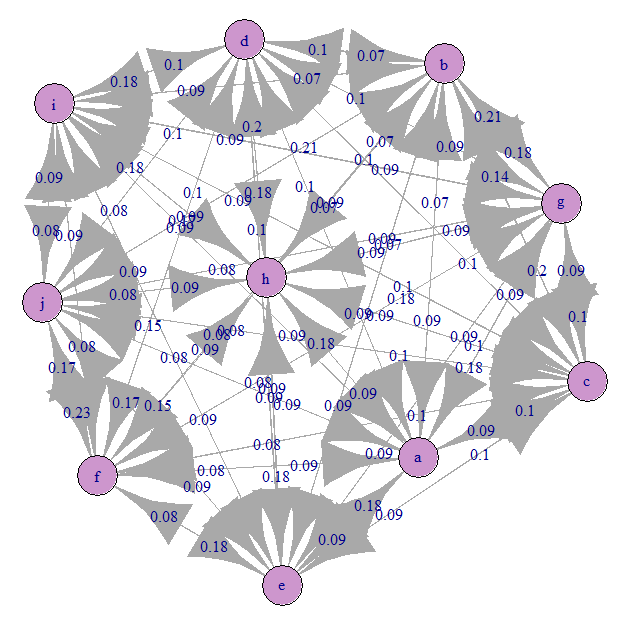
सब कुछ लगभग समान रूप से भ्रमित है)। ऐसा इसलिए है क्योंकि हमने परिवर्तनीय परिवर्तन निर्दिष्ट किए हैं।

और अब जादू का समय है!

 ## calculate pagerank ei <- eigen(A) as.numeric(ei$values[1]) pr <- as.numeric(ei$vectors[,1] / sum(ei$vectors[,1])) sum(pr) names(pr) <- node_names print(round(pr, 2)) 

स्टोकेस्टिक मैट्रिक्स ए के लिए, पहला आइगेनवेल्यू एकता के बराबर होना चाहिए, और संबंधित आइगेनवेक्टर पेजरैंक वेक्टर है।

> प्रिंट (गोल (पीआर, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

यह पीआर मानों का सदिश है - यह संक्रमण मैट्रिक्स ए का सामान्यीकृत आइजनवेक्टर है, जो इस मैट्रिक्स के आइगेनवेल्यू के साथ एकता के बराबर है - प्रमुख ईजनवेक्टर।

अब आप तत्वों को रैंक कर सकते हैं। लेकिन प्रयोग की बारीकियों के कारण, उनका वजन काफी समान है।

बिजली की विधि का उपयोग कर समस्याओं और उनके समाधान

संक्रमण मैट्रिक्स A स्टोचैस्टिस स्थितियों को संतुष्ट नहीं कर सकता है।

सबसे पहले, ऐसे तत्व हो सकते हैं जो कहीं भी संदर्भित नहीं करते हैं, अर्थात प्रतिक्रिया की अनुपस्थिति के साथ (वे उन्हें संदर्भित कर सकते हैं)। बड़े वास्तविक रेखांकन के लिए यह एक समस्या है। इसका मतलब यह है कि मैट्रिक्स के स्तंभों में से एक में केवल शून्य होगा। इस मामले में, eigenvectors के माध्यम से समाधान काम नहीं करेगा।

Google ने एक समान संभाव्यता वितरण p = 1 / N के साथ एक कॉलम भरकर इस समस्या को हल किया। जहाँ N सभी तत्वों की संख्या है।

 dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) 

दूसरे, ग्राफ़ में एक दूसरे के प्रति प्रतिक्रिया वाले तत्व हो सकते हैं, लेकिन ग्राफ़ के शेष तत्व नहीं। यह मान्यताओं के उल्लंघन के कारण रैखिक बीजगणित के लिए भी एक दुर्गम समस्या है।

यह एक निरंतरता नामक डंपिंग कारक को पेश करके हल किया जाता है, जो किसी भी तत्व से किसी भी अन्य के लिए एक संक्रमण की प्राथमिकता संभावना को इंगित करता है, भले ही कोई भौतिक लिंक न हो। दूसरे शब्दों में, किसी भी अवस्था में प्रसार संभव है।

 d = 0.15 #damping factor (to ensure algorithm convergence) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix 

यदि हम अपने मैट्रिक्स में इन परिवर्तनों को लागू करते हैं, तो इसे फिर से eigenvectors के माध्यम से हल किया जा सकता है!

तीसरा, कॉर्न मैट्रिक्स चौकोर नहीं हो सकता है, लेकिन यह महत्वपूर्ण है! मैं इस क्षण पर ध्यान केंद्रित नहीं करूंगा, क्योंकि मेरा मानना ​​है कि आप स्वयं यह पता लगाएंगे कि इसे कैसे ठीक किया जाए।

लेकिन एक तेज़ और अधिक सटीक तरीका है, जो मेमोरी में अधिक किफायती है (जो बड़े ग्राफ़ के लिए प्रासंगिक हो सकता है): पावर विधि।

 ## pagerank function (tested on example from tutorial) rm(pagerank_func) pagerank_func <- function( A #transition matrix , eps = 0.00001 #sufficiently small error , d = 0.15 #damping factor (to ensure algorithm convergence) ) { dim.1 <- dim(A)[1] A <- as.data.table(A) nul_cols <- apply(A, 2, function(x) sum(x) == 0) if( sum(nul_cols) > 0 ) { A[ , (colnames(A)[nul_cols]) := lapply(.SD, function(x) 1 / dim.1) , .SDcols = colnames(A)[nul_cols] ] } A <- as.matrix(A) M <- (1 - d) * A + d * (1 / dim.1 * matrix(1, nrow = dim.1, ncol = dim.1)) # google matrix rank = as.numeric(rep(1 / dim.1, dim.1)) ## iterate until convergence while( sum( (rank - M %*% rank) ^ 2 ) > eps ) { rank <- M %*% rank } return(rank) } pr2 <- pagerank_func(A) pr2=as.vector(pr2) names(pr2)=node_names 

देखा!

> प्रिंट (गोल (पीआर, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11
> प्रिंट (राउंड (pr2, 2))
abcdefghij
0.09 0.11 0.09 0.10 0.10 0.11 0.10 0.11 0.08 0.11

इस पर मैं ट्यूटोरियल को समाप्त कर दूंगा। मुझे आशा है कि आप इसे उपयोगी पाएंगे।

मैं यह कहना भूल गया कि परिवर्तन (संभावनाओं) का एक मैट्रिक्स बनाने के लिए, आप ग्रंथों की समानता, संदर्भों की संख्या, एक लिंक के तथ्य, और अन्य मैट्रिक्स का उपयोग कर सकते हैं जो छद्म संभावनाओं की ओर ले जाते हैं या संभावनाएं हैं। पूरे पाठ को संक्षेप में प्रस्तुत करने वाले वाक्य को उजागर करने के लिए शब्द बैग tf-idf की समानता मैट्रिक्स पर पाठ में वाक्यों की रैंकिंग दिलचस्प उदाहरण है। पीआर के अन्य रचनात्मक उपयोग हो सकते हैं।

मैं अपने आप को संक्रमण मैट्रिक्स के साथ खेलने की कोशिश करने की सलाह देता हूं और सुनिश्चित करता हूं कि आपको शांत पीआर मान मिले, जो व्याख्या करना भी काफी आसान है।

यदि आप मेरे साथ गलतियाँ या त्रुटियां देखते हैं - टिप्पणियों या संदेश में इंगित करें, और मैं सब कुछ ठीक कर दूंगा।

सभी कोड यहाँ संकलित हैं:


पुनश्च: इस पूरे विचार को अन्य भाषाओं में भी आसानी से लागू किया जाता है, कम से कम पायथन में, मैंने बिना किसी कठिनाई के सब कुछ किया।