जूलिया और समन्वित वंश विधि

समन्वय-वार वंश की विधि बहुआयामी अनुकूलन का सबसे सरल तरीकों में से एक है और अपेक्षाकृत चिकनी स्थलाकृति के साथ स्थानीय न्यूनतम कार्यों को खोजने का एक अच्छा काम करता है, इसलिए बेहतर होगा कि आप स्वयं को इसके अनुकूलन तरीकों से परिचित करना शुरू करें।

एक्स्ट्रीम की खोज समन्वय अक्षों की दिशा में की जाती है, अर्थात खोज प्रक्रिया के दौरान, केवल एक समन्वय बदला जाता है। इस प्रकार, एक बहुआयामी समस्या एक आयामी एक को कम कर देती है।

एल्गोरिथ्म

पहला चक्र:

• $$$x_1 = var$। $$$x_2 = x_2 ^ 0$। $$$x_3 = x_3 ^ 0$,, ... $$$x_n = x_n ^ 0$।
• चरम कार्यों के लिए देख रहे हैं $$$f (x_1)$। फ़ंक्शन के चरम पर बिंदु पर रखें $$$x_1 ^ 1$।
• $$$x_1 = x_1 ^ 1$। $$$x_2 = var$। $$$x_3 = x_3 ^ 0$,, ... $$$x_n = x_n ^ 0$। एक्स्ट्रीमम फ़ंक्शन $$$f (x_2)$के बराबर है $$$x_2 ^ 1$
• ...
• $$$x_1 = x_1 ^ 1$। $$$x_2 = x_2 ^ 1$। $$$x_3 = x_3 ^ 1$,, ... $$$x_n = var$।
  एन चरणों के प्रदर्शन के परिणामस्वरूप, चरम पर दृष्टिकोण का एक नया बिंदु मिला $$$(x_1 ^ 1, x_2 ^ 1, ..., x_n ^ 1)$। अगला, हम खाते के अंत के लिए मानदंड की जांच करते हैं: यदि यह पूरा हो जाता है, तो समाधान पाया जाता है, अन्यथा हम एक और चक्र करते हैं।

ट्रेनिंग

पैकेज संस्करणों की जाँच करें:

(v1.1) pkg> status Status `C:\Users\User\.julia\environments\v1.1\Project.toml` [336ed68f] CSV v0.4.3 [a93c6f00] DataFrames v0.17.1 [7073ff75] IJulia v1.16.0 [47be7bcc] ORCA v0.2.1 [58dd65bb] Plotly v0.2.0 [f0f68f2c] PlotlyJS v0.12.3 [91a5bcdd] Plots v0.23.0 [ce6b1742] RDatasets v0.6.1 [90137ffa] StaticArrays v0.10.2 [8bb1440f] DelimitedFiles [10745b16] Statistics 

हम सतह या स्तर रेखाओं को खींचने के लिए एक फ़ंक्शन को परिभाषित करते हैं जिसमें यह ग्राफ की सीमाओं को समायोजित करने के लिए सुविधाजनक होगा:

 using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end 

एक मॉडल फ़ंक्शन के रूप में, हम एक अण्डाकार पैराबोलाइड चुनते हैं

 parabol(x) = sum(u->u*u, x) fun = parabol plotter(surface, low = [-1 -1], up = [1 1]) 

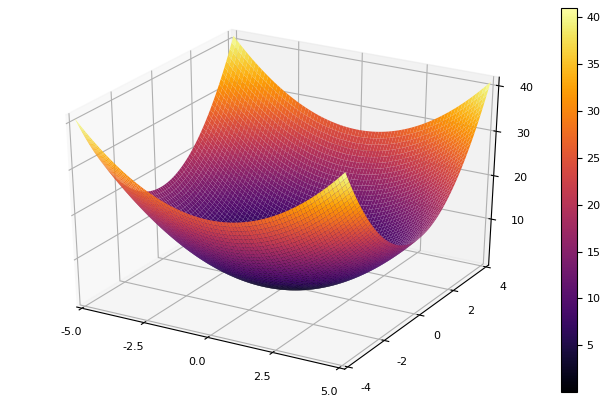
समन्वित वंश

हम एक फ़ंक्शन में विधि को लागू करते हैं जो एक आयामी अनुकूलन विधि, समस्या का आयाम, वांछित त्रुटि, प्रारंभिक सन्निकटन और ड्राइंग स्तर लाइनों के लिए प्रतिबंधों का नाम लेता है। सभी पैरामीटर डिफ़ॉल्ट मानों पर सेट हैं।

 function ofDescent(odm; ndimes = 2, ε = 1e-4, fit = [.5 .5], low = [-1 -1], up = [1 1]) k = 1 #      sumx = 0 sumz = 1 plotter(contour, low = low, up = up) #    x = [ fit[1] ] #     y = [ fit[2] ] #      while abs(sumz - sumx) > ε && k<80 fitz = copy(fit) for i = 1:ndimes odm(i, fit, ε) #    end push!(x, fit[1]) push!(y, fit[2]) sumx = sum(abs, fit ) sumz = sum(abs, fitz) #println("$k $fit") k += 1 end #     scatter!(x', y', legend = false, marker=(10, 0.5, :orange) );# , ,  p = title!("Age = $(size(x,1)) f(x,y) = $(fun(fit))") end 

अगला, हम एक-आयामी अनुकूलन के विभिन्न तरीकों की कोशिश करेंगे

न्यूटन की विधि

$$

$$x_ {n + 1} = x_n - \ frac {f (x_n)} {f '(x_n)}$$

कार्यान्वयन के रूप में विधि का विचार सरल है

 #  dfun = (x, i) -> i == 1 ? 2x[1] + x[2]*x[2] : 2x[2] + x[1]*x[1] function newton2(i, fit, ϵ) k = 1 oldfit = Inf while ( abs(fit[i] - oldfit) > ϵ && k<50 ) oldfit = fit[i] tryfit = fun(fit) / dfun(fit, i) fit[i] -= tryfit println(" $k $fit") k+=1 end end ofDescent(newton2, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

न्यूटन शुरुआती सन्निकटन पर काफी मांग कर रहा है, और चरणों पर सीमा के बिना, वह आसानी से अज्ञात दूरियों की सवारी कर सकता है। व्युत्पन्न की गणना वांछनीय है, लेकिन छोटे बदलाव के साथ तिरस्कृत किया जा सकता है। हम अपने कार्य को संशोधित करते हैं:

 function newton(i, fit, ϵ) k = 1 oldfit = Inf x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) while ( abs(oldfit - fit[i]) > ϵ && k<50 ) fx = fun(fit) oldfit = fit[i] fit[i] += 0.01 dfx = fun(fit) fit[i] -= 0.01 tryfit = fx*0.01 / (dfx-fx) #        if( abs(tryfit) > abs(fit[i])*10 ) push!(x, fit[1]) push!(y, fit[2]) break end fit[i] -= tryfit #println(" $k $fit") push!(x, fit[1]) push!(y, fit[2]) k+=1 end #  - -   plot!(x, y, w = 3, legend = false, marker = :rect ) end ofDescent(newton, fit = [9.1 9.1], low = [-4 -4], up = [13 13]) 

उलटा परवलय प्रक्षेप

एक विधि जिसे व्युत्पन्न के ज्ञान की आवश्यकता नहीं है और इसका अच्छा अभिसरण है

 function ipi(i, fit, ϵ) # inverse parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.15 xn[i] = fit[i] + 0.15 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<80 fn = fun(xn) a = fn1*fn / ( (fn2-fn1)*(fn2-fn ) ) b = fn2*fn / ( (fn1-fn2)*(fn1-fn ) ) c = fn2*fn1 / ( (fn -fn2)*(fn -fn1) ) xnp[i] = a*xn2[i] + b*xn1[i] + c*xn[i] xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(ipi, fit = [0.1 0.1], low = [-.1 -.1], up = [.4 .4]) 

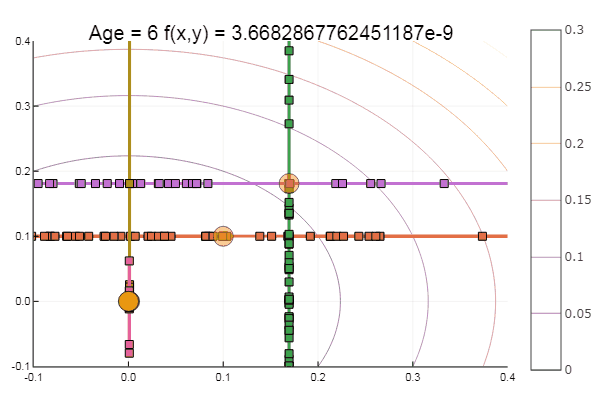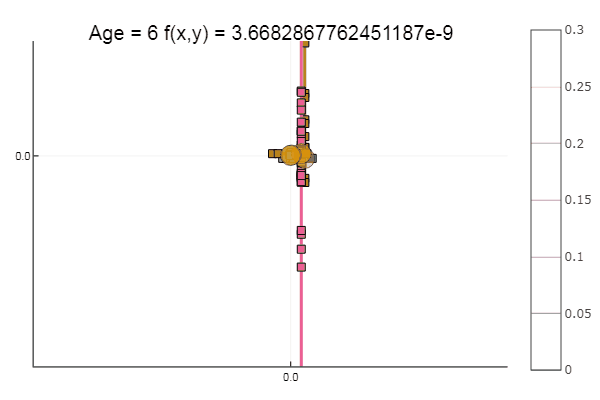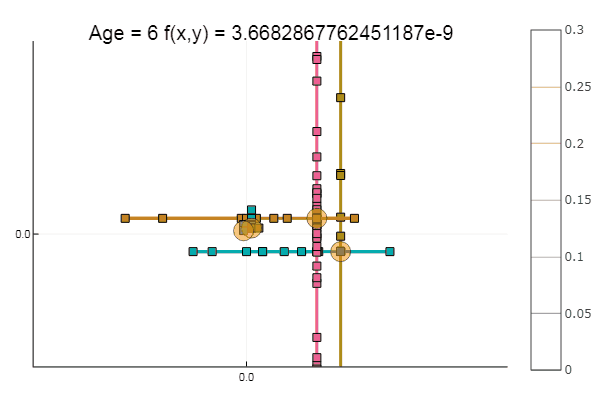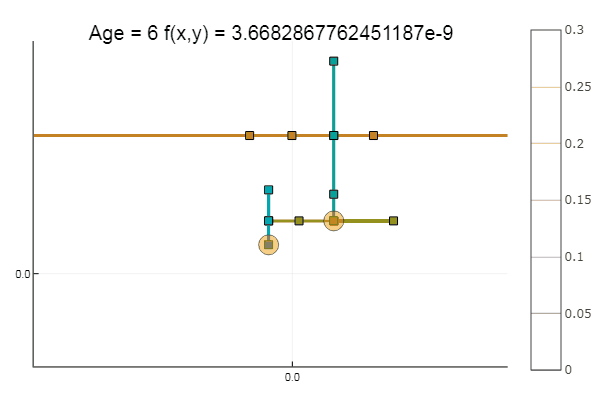
यदि हम प्रारंभिक सन्निकटन को बदतर बनाते हैं, तो विधि को समन्वित वंश के प्रत्येक युग के लिए कई चरणों की आवश्यकता होगी। इस संबंध में, उसका भाई जीतता है

अनुक्रमिक परवलयिक अंतर्वेशन

इसके लिए तीन शुरुआती बिंदु भी आवश्यक हैं , लेकिन कई परीक्षण कार्यों पर यह अधिक संतोषजनक परिणाम दिखाता है।

 function spi(i, fit, ϵ) # sequential parabolic interpolation n = 0 xn2 = copy(fit) xn1 = copy(fit) xn = copy(fit) xnp = zeros( length(fit) ) xy = copy(fit) xn2[i] = fit[i] - 0.01 xn[i] = fit[i] + 0.01 fn2 = fun(xn2) fn1 = fun(xn1) while abs(xn[i] - xn1[i]) > ϵ && n<200 fn = fun(xn) v0 = xn1[i] - xn2[i] v1 = xn[i] - xn2[i] v2 = xn[i] - xn1[i] s0 = xn1[i]*xn1[i] - xn2[i]*xn2[i] s1 = xn[i] *xn[i] - xn2[i]*xn2[i] s2 = xn[i] *xn[i] - xn1[i]*xn1[i] xnp[i] = 0.5(fn2*s2 - fn1*s1 + fn*s0) / (fn2*v2 - fn1*v1 + fn*v0) xn2[i] = xn1[i] xn1[i] = xn[i] xn[i] = xnp[i] fn2 = fn1 fn1 = fn n += 1 println(" $n $xn $xn1") xy = [xy; xn] end fit[i] = xnp[i] plot!(xy[:,1], xy[:,2], w = 3, legend = false, marker = :rect ) end ofDescent(spi, fit = [16.1 16.1], low = [-.1 -.1], up = [.4 .4]) 

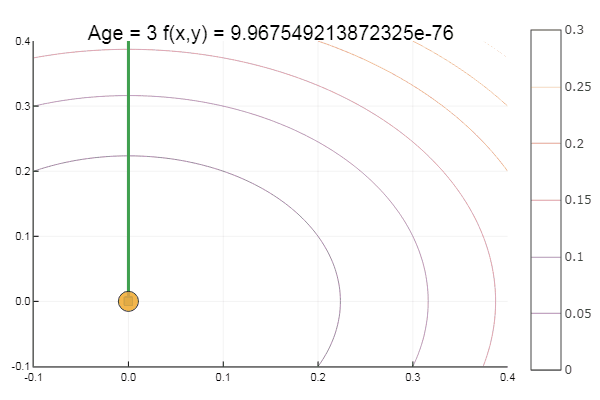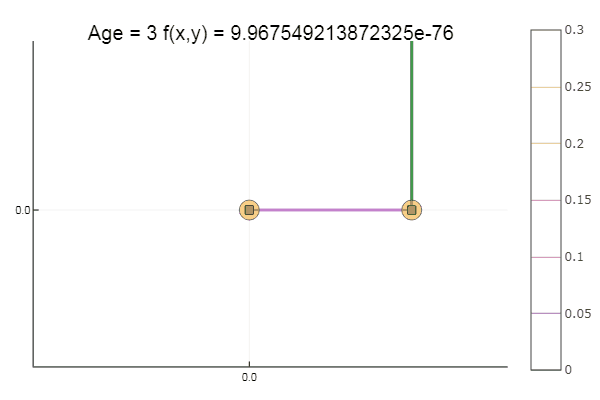
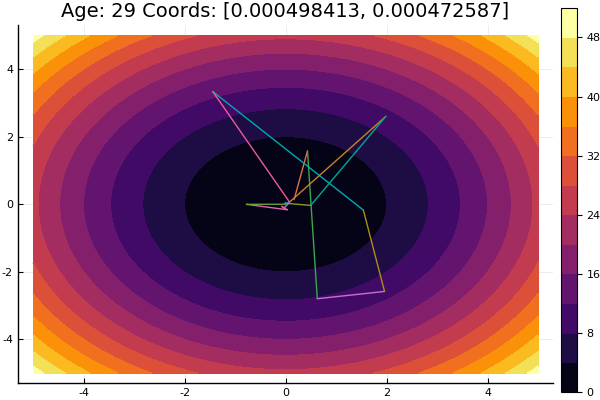
तीन चरणों में एक बहुत भद्दा शुरुआती बिंदु से बाहर कदम आया! अच्छा ... लेकिन सभी तरीकों में एक खामी है - वे एक स्थानीय न्यूनतम में कनवर्ट करते हैं। अब आइए अनुसंधान के लिए एकली के कार्य को लें

$$

$$f (x, y) = - 20 \ exp \ left [-0.2 {\ sqrt {0.5 \ बाएँ (x ^ {2} + y ^ {2} \ right)}} \ right] - \ exp \ left [ 0.5 \ बाएँ (\ cos 2 \ pi x + \ cos 2 \ pi y \ right) \ right] + e + 20$$

 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly plotter(surface, low = [-5 -5], up = [5 5]) 

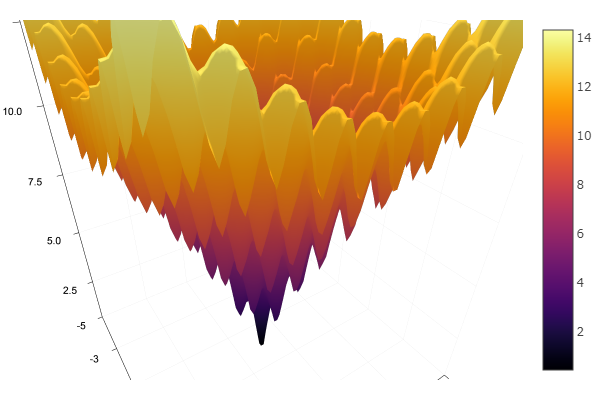
 ofDescent(spi, fit = [1.4 1.4], low = [-.1 -.1], up = [2.4 2.4]) 

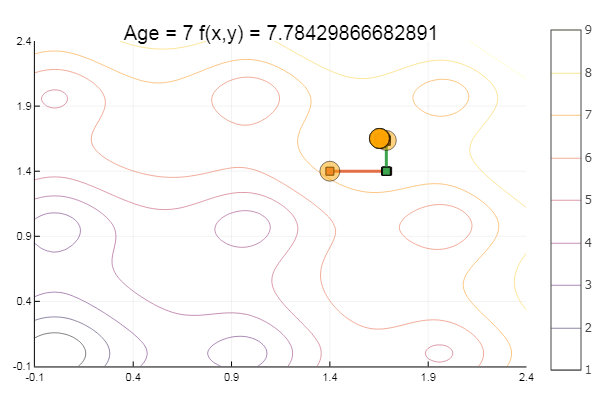
स्वर्ण अनुपात विधि

सिद्धांत । हालांकि कार्यान्वयन जटिल है, लेकिन कभी-कभी स्थानीय मिनिमा कूदकर विधि खुद को अच्छी तरह दिखाती है

 function interval(i, fit, st) d = 0. ab = zeros(2) fitc = copy(fit) ab[1] = fitc[i] Fa = fun(fitc) fitc[i] -= st Fdx = fun(fitc) fitc[i] += st if Fdx < Fa st = -st end fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) while Fb < Fa d = ab[1] ab[1] = ab[2] Fa = Fb fitc[i] += st ab[2] = fitc[i] Fb = fun(fitc) # println("----", Fb, " ", Fa) end if st < 0 c = ab[2] ab[2] = d d = c end ab[1] = d ab end function goldsection(i, fit, ϵ) ϕ = Base.MathConstants.golden ab = interval(i, fit, 0.01) α = ϕ*ab[1] + (1-ϕ)*ab[2] β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = α Fa = fun(fit) fit[i] = β Fb = fun(fit) while abs(ab[2] - ab[1]) > ϕ if Fa < Fb ab[2] = β β = α Fb = Fa α = ϕ*ab[1] + (1-ϕ)*ab[2] fit[i] = α Fa = fun(fit) else ab[1] = α α = β Fa = Fb β = ϕ*ab[2] + (1-ϕ)*ab[1] fit[i] = β Fb = fun(fit) end println(">>>", i, ab) plot!(ab, w = 1, legend = false, marker = :rect ) end fit[i] = 0.5(ab[1] + ab[2]) end ofDescent(goldsection, fit = [1.4 1.4], low = [-.1 -.1], up = [1. 1.]) 

यह सभी समन्वित वंश के साथ है। प्रस्तुत विधियों के एल्गोरिदम काफी सरल हैं, इसलिए उन्हें अपनी पसंदीदा भाषा में लागू करना मुश्किल नहीं है। भविष्य में, आप जूलिया भाषा के अंतर्निहित उपकरणों पर विचार कर सकते हैं, लेकिन अब आप अपने हाथों से सब कुछ महसूस करना चाहते हैं, इसलिए बोलने के लिए, तरीकों को अधिक जटिल और अधिक कुशल मानते हैं, तो आप वैश्विक अनुकूलन पर जा सकते हैं, साथ ही साथ किसी अन्य भाषा में कार्यान्वयन के साथ तुलना कर सकते हैं।

साहित्य

1. भौतिकविदों के लिए संख्यात्मक तरीके ज़ैतसेव वी.वी. Nonlinear समीकरण और अनुकूलन: एक ट्यूटोरियल। - समारा, 2005 - 86 एस।
2. ऑप्टिकल सिस्टम के अनुकूलन के लिए इवानोव ए.वी. गाइड का अध्ययन करें। -एसपीबी: एसपीएसएसयू आईटीएमओ, 2010 - 114 एस।
3. पोपोवा टी। एम। बहुआयामी अनुकूलन के तरीके: दिशा-निर्देश "अनुप्रयुक्त गणित" / COMP के छात्रों के लिए अनुशासन "अनुकूलन के तरीके" में प्रयोगशाला के काम के लिए दिशा-निर्देश और कार्य। टी। एम। पोपोवा - खाबरोवस्क: पब्लिशिंग हाउस ऑफ द पैसिफिक। राज्य। विश्वविद्यालय, 2012 ।-- 44 पी।