जूलिया, ग्रेडिएंट डिसेंट और सिम्पलेक्स विधि

हम बहुआयामी अनुकूलन विधियों के साथ अपने परिचित को जारी रखते हैं ।

अगला, निष्पादन की गति के विश्लेषण के साथ सबसे तेज वंश विधि का कार्यान्वयन, साथ ही जूलिया और सी ++ भाषा के माध्यम से नेल्डर-मीड पद्धति का कार्यान्वयन प्रस्तावित है।

क्रमिक वंश विधि

एक्सट्रीम की खोज ग्रेडिएंट (अधिकतम) या एंटी-ग्रेडिएंट (मिनट) की दिशा में चरणों में की जाती है। ग्रेडिएंट (एंटी-ग्रेडिएंट) की दिशा में प्रत्येक चरण पर, फ़ंक्शन बढ़ने (घटने) तक आंदोलन किया जाता है।

सिद्धांत के लिए, लिंक का अनुसरण करें:

• धीरे-धीरे उतरना
• संयुग्मन विधि
• नेल्डर-मीड विधि
• ग्रेडिएंट मेथड्स ओवरव्यू
• SciPy, अनुकूलन
• बाधाओं के साथ समस्याओं के लिए गणितीय अनुकूलन के बुनियादी तरीकों का अवलोकन
• नेल्डर-मीड अनुकूलन विधि। पायथन कार्यान्वयन
• भौतिकविदों के लिए संख्यात्मक तरीके ज़ैतसेव वी.वी. गैर-रेखीय समीकरण और अनुकूलन
  एक आधार के रूप में, अंतिम स्रोत से उदाहरणों का उपयोग किया गया था।

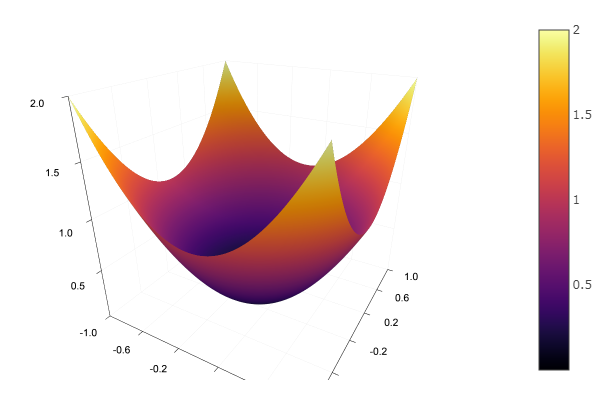
मॉडल फ़ंक्शन के साथ, हम एक अण्डाकार पैराबोलाइड चुनते हैं और राहत प्रदान करने का कार्य निर्धारित करते हैं:

using Plots plotly() #   function plotter(plot_fun; low, up) Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for x in Xs, y in Ys ]; plot_fun(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) #   yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) end parabol(x) = sum(u->u*u, x) #   fun = parabol plotter(surface, low = [-1 -1], up = [1 1]) 

हम एक फ़ंक्शन को परिभाषित करते हैं, जो सबसे सरल वंश विधि को लागू करता है, जो समस्या, सटीकता, चरण की लंबाई, प्रारंभिक सन्निकटन और बाउंडिंग बॉक्स फ्रेम के आकार का आयाम लेता है:

 # -- ,     -   function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) end #println(fun(fit)) end 

आप अनुकूलन के संदर्भ में ढाल की दिशा की गणना करने वाले फ़ंक्शन पर ध्यान केंद्रित कर सकते हैं।

पहली बात जो मन में आती है वह है मेट्रिसेस के साथ क्रिया:

 # \delta -      #      function grad(fit, δ) ndimes = length(fit) Δ = zeros(ndimes, ndimes) for i = 1:ndimes Δ[i,i] = δ end fr = [ fun( fit + Δ[:,i] ) for i=1:ndimes] fl = [ fun( fit - Δ[:,i] ) for i=1:ndimes] g = 0.5(fr - fl)/δ modg = sqrt( sum(x -> x*x, g) ) g /= modg end 

जूलिया वास्तव में कितना अच्छा है कि समस्या वाले क्षेत्रों का आसानी से परीक्षण किया जा सकता है:

 #]add BenchmarkTools using BenchmarkTools @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 44.14 KiB allocs estimate: 738 -------------- minimum time: 76.973 μs (0.00% GC) median time: 81.315 μs (0.00% GC) mean time: 92.828 μs (9.14% GC) maximum time: 5.072 ms (94.37% GC) -------------- samples: 10000 evals/sample: 1 

आप Sishny स्टाइल में सब कुछ फिर से करने के लिए जल्दी कर सकते हैं

 function grad(fit::Array{Float64,1}, δ::Float64) ndimes::Int8 = 2 g = zeros(ndimes) modg::Float64 = 0. Fr::Float64 = 0. Fl::Float64 = 0. for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= 2δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ modg += g[i]*g[i] end modg = sqrt( modg ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 14.06 KiB allocs estimate: 325 -------------- minimum time: 29.210 μs (0.00% GC) median time: 30.395 μs (0.00% GC) mean time: 33.603 μs (6.88% GC) maximum time: 4.287 ms (98.88% GC) -------------- samples: 10000 evals/sample: 1 

लेकिन जैसा कि यह पता चला है, यह खुद और हमारे बिना जानता है कि किस प्रकार का सेट होना चाहिए, इसलिए हम एक समझौता करते हैं:

 function grad(fit, δ) #    ndimes = length(fit) g = zeros(ndimes) for i = 1:ndimes fit[i] += δ Fr = fun(fit) fit[i] -= δ fit[i] -= δ Fl = fun(fit) fit[i] += δ g[i] = 0.5(Fr - Fl)/δ end modg = sqrt( sum(x -> x*x, g) ) g /= modg end @benchmark ofGradient() BenchmarkTools.Trial: memory estimate: 15.38 KiB allocs estimate: 409 -------------- minimum time: 28.026 μs (0.00% GC) median time: 30.394 μs (0.00% GC) mean time: 33.724 μs (6.29% GC) maximum time: 3.736 ms (98.72% GC) -------------- samples: 10000 evals/sample: 1 

अब उसे ड्रा करें:

 function ofGradient(; ndimes = 2, ε = 1e-4, st = 0.9, fit = [9.9, 9.9], low = [-1 -1], up = [10 10]) k = 0 x = [] y = [] push!(x, fit[1]) push!(y, fit[2]) plotter(contour, low = low, up = up) while st > ε g = grad(fit, 0.01) fung = fun(fit) fit -= st*g if fun(fit) >= fung st *= 0.5 fit += st*g end k += 1 #println(k, " ", fit) push!(x, fit[1]) push!(y, fit[2]) end plot!(x, y, w = 3, legend = false, marker = :rect ) title!("Age = $kf(x,y) = $(fun(fit))") println(fun(fit)) end ofGradient() 

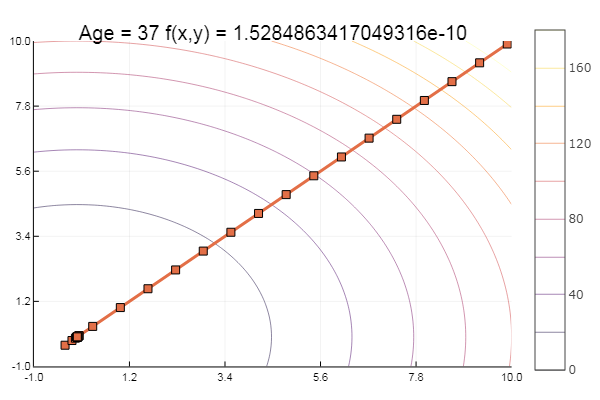
अब आइए एक्ले के कार्यों पर प्रयास करें:

 ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] fun = ekly ofGradient(fit = [4.3, 4.9], st = 0.1, low = [3 4.5], up = [4.5 5.4] ) 

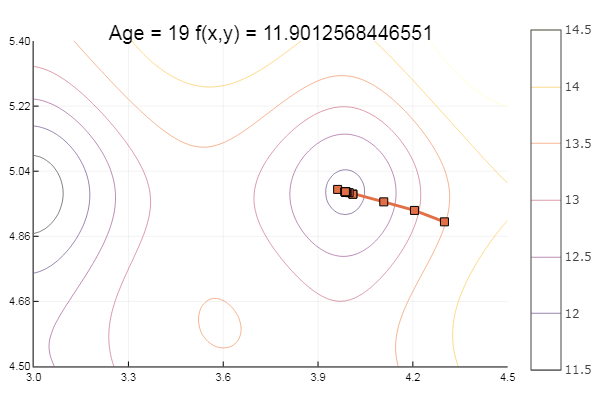
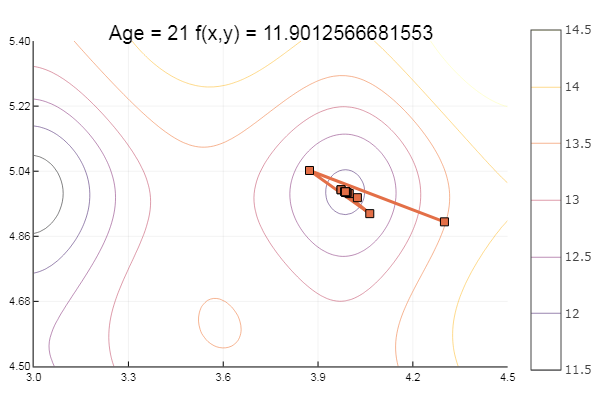
एक स्थानीय न्यूनतम में गिर गया। चलो और कदम उठाएँ:

 ofGradient(fit = [4.3, 4.9], st = 0.9, low = [3 4.5], up = [4.5 5.4] ) 

 ofGradient(fit = [4.3, 4.9], st = 1.9, low = [-5.2 -2.2], up = [8.1 7.1] ) 

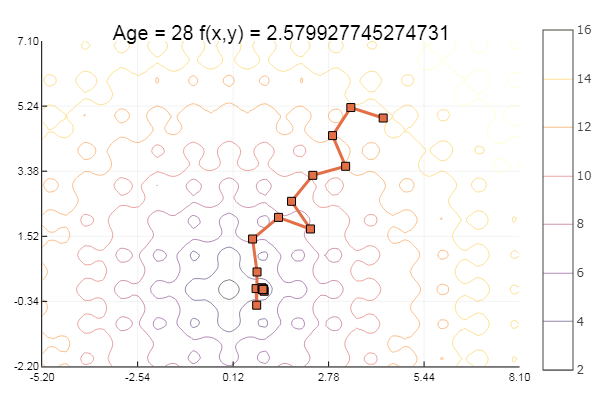
... और थोड़ा और:

 ofGradient(fit = [4.3, 4.9], st = 8.9, low = [-5.2 -2.2], up = [8.1 7.1] ) 

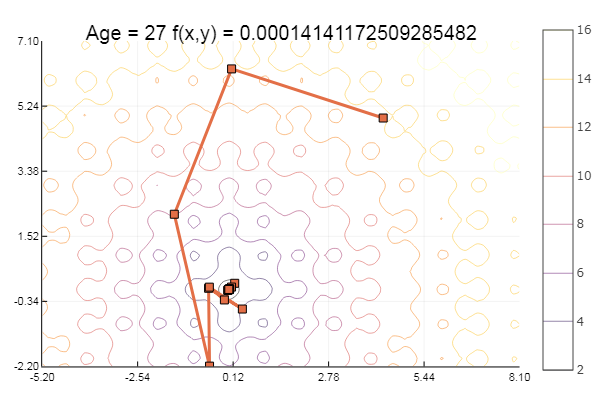
बहुत बढ़िया! और अब एक खड्ड के साथ कुछ, जैसे कि रोसेनब्रोक फ़ंक्शन:

 rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] fun = rosenbrok plotter(surface, low = [-2 -1.5], up = [2 1.5]) 

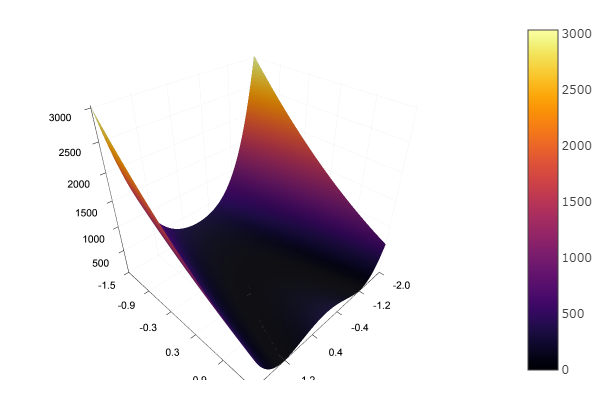
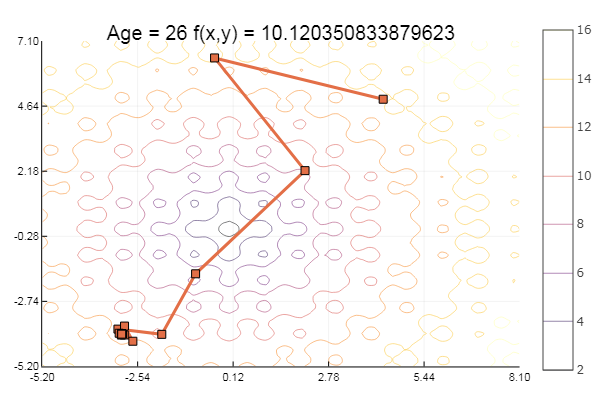
 ofGradient(fit = [2.3, 2.2], st = 9.9, low = [-5.2 -5.2], up = [8.1 7.1] ) 

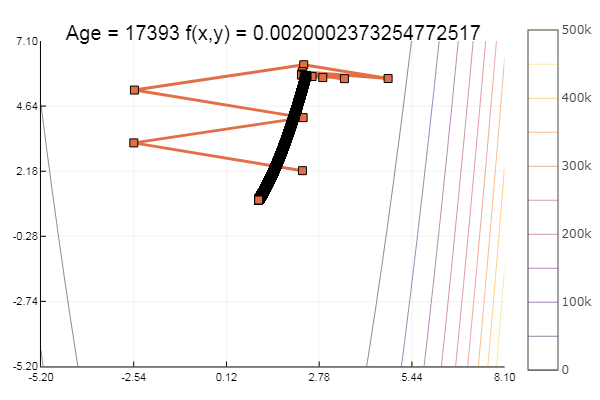
 ofGradient(fit = [2.3, 2.2], st = 0.9, low = [-5.2 -5.2], up = [8.1 7.1] ) 

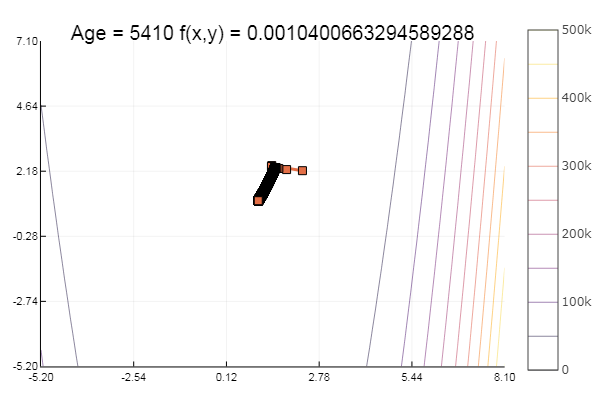
नैतिकता: ढालों को कैनोपीज़ पसंद नहीं है।

सिंप्लेक्स विधि

नेल्डर-मीड विधि, जिसे विरूपित पॉलीहेड्रॉन विधि और सिम्पलेक्स विधि के रूप में भी जाना जाता है, कई प्रकारों के एक फ़ंक्शन के बिना शर्त अनुकूलन की एक विधि है जो फ़ंक्शन के व्युत्पन्न (अधिक सटीक, ग्रेडिएंट) का उपयोग नहीं करती है, और इसलिए nonsmooth और / या शोर कार्यों के लिए आसानी से लागू होती है।

विधि का सार एक चरम बिंदु के आसपास एक सिंप्लेक्स के अनुक्रमिक आंदोलन और विरूपण है।

विधि एक स्थानीय चरम सीमा को ढूंढती है और उनमें से एक में फंस सकती है। यदि आपको अभी भी वैश्विक चरम सीमा खोजने की आवश्यकता है, तो आप एक अलग प्रारंभिक सिंप्लेक्स चुनने की कोशिश कर सकते हैं।

सहायक कार्य:

 #          function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] #Return a permutation vector I that puts v[I] in sorted order. end #   function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) vecl(x) = sqrt( sum(u -> u*u, x) )#   for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function simplexplot(xy, low, up) for i = 1:length(xy) if i%11 == 0 low *= 0.05 up *= 0.05 end Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] contour(Xs, Ys, Zs) xaxis!( low[1]:(up[1]-low[1])*0.2:up[1] ) yaxis!( low[2]:(up[2]-low[2])*0.2:up[2] ) plot!(xy[i][1,:], xy[i][2,:], w = 3, legend = false, marker = :circle ) title!("Age = $if(x,y) = $(fun(xy[i][:,1]))") savefig("$fun $i.png") end end 

और स्वयं सरल विधि:

 function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) vecl(v) = sqrt( sum(x -> x*x, v) ) k = 0 N = ndimes Xx = zeros(N, N+1) coords = [] for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end #println(k, " ", p, " ", Xx[:,1]) push!(coords, [Xx[:,1:3] Xx[:,1] ]) p = normx(Xx) end #while #simplexplot(coords, low, up) fit = Xx[:,1] end ofNelderMid(fit = [-9, -2], low = [-2 2], up = [-8 8]) 

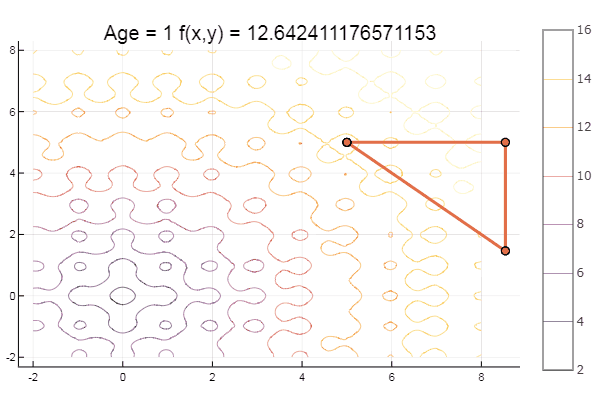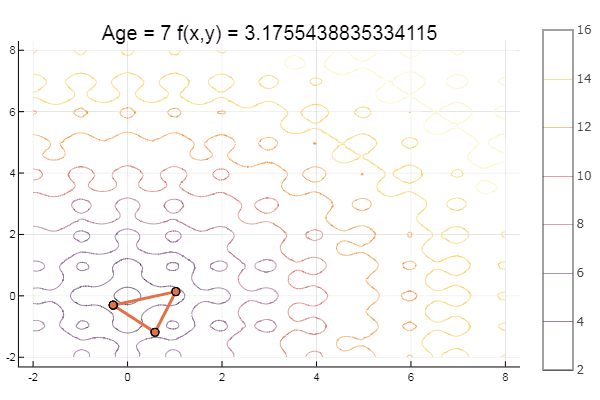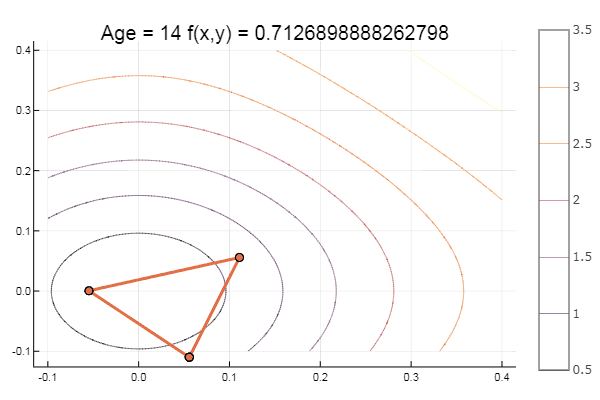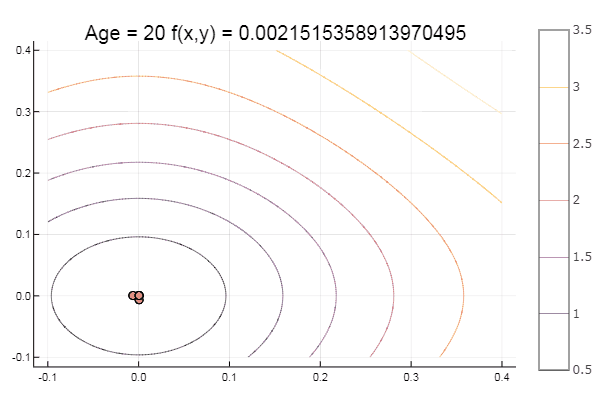
और मिठाई के लिए कुछ बीच ... उदाहरण के लिए, बुकिन का कार्य
$$$f (x, y) = 100 \ sqrt {| y-0.01x ^ 2 |} + 0.01 | x + 10$

 bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] fun = bukin6 ofNelderMid(fit = [-10, -2], low = [-3 -7], up = [-8 -4.5]) 

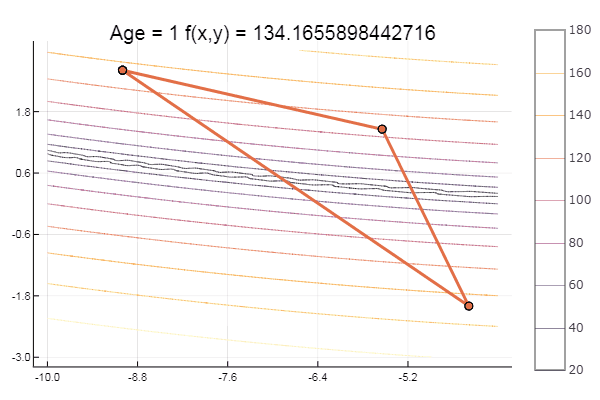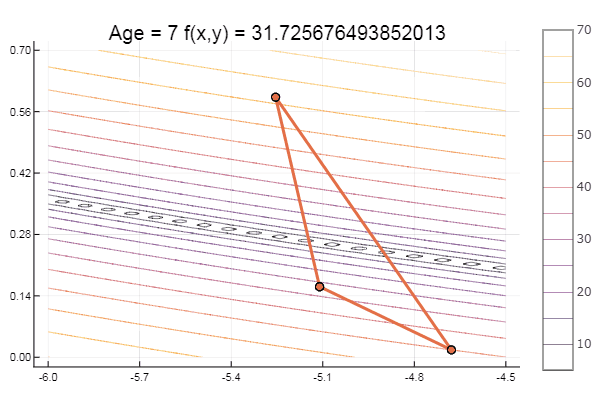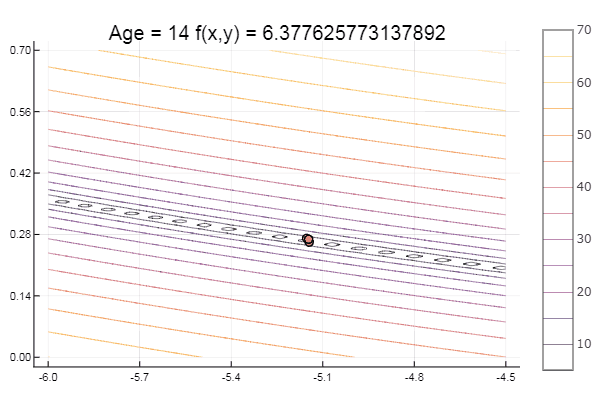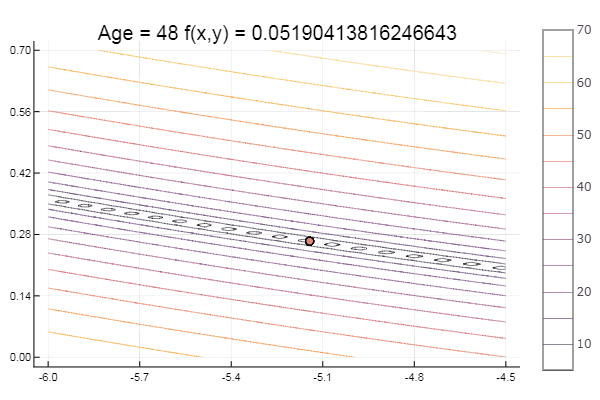
स्थानीय न्यूनतम - ठीक है, कुछ भी नहीं, मुख्य बात यह है कि सही शुरुआती सिम्प्लेक्स चुनना है, इसलिए खुद के लिए मुझे एक पसंदीदा मिला।

बोनस। नेल्डर-मीड के तरीके, सी ++ में सबसे तेज वंश और समन्वित वंश

 /* * File: main.cpp * Author: User * * Created on 3  2017 ., 21:22 */ #include <iostream> #include <math.h> using namespace std; typedef double D; class Model { public: D *fit; D ps; Model(); DI(); }; Model :: Model() { ps = 1; fit = new D[3]; fit[0]=1.3; fit[1]=1.; fit[2]=2.; } D Model :: I() // rosenbrock { return 100*(fit[1]-fit[0]*fit[0]) * (fit[1]-fit[0]*fit[0]) + (1-fit[0])*(1-fit[0]); } class Methods : public Model { public: void ofDescent(); void Newton(int i); void SPI(int i); //sequential parabolic interpolation void Cutters(int i); void Interval(D *ab, D st, int i); void Gold_section(int i); void ofGradient(); void Grad(int N, D *g, D delta); void Srt(D **X, int N); void ofNelder_Mid(); D Nor(D **X, int N); }; void Methods :: ofDescent()//   { int i, j=0; D *z = new D[3]; D sumx, sumz; sumx = sumz = 0; do { sumx = sumz = 0; for(i=0; i<3; i++) z[i] = fit[i]; for(i=0; i<2; i++) { //Cutters(i); //SPI(i); Newton(i); //Gold_section(i); sumx += fit[i]; sumz += z[i]; } j++; //if(j%1000==0) cout << j << " " << fit[0] << " " << fit[1] << " " << fit[2] << " " << fit[3] << endl; //cout << sumz << " " << sumx << endl; } while(fabs(sumz - sumx) > 1e-6); delete[]z; } void Methods :: SPI(int i) { int k = 2; D f0, f1, f2; D v0, v1, v2; D s0, s1, s2; D *X = new D[300]; X[0] = fit[i] + 0.01; X[1] = fit[i]; X[2] = fit[i] - 0.01; while(fabs(X[k] - X[k-1]) > 1e-3) { fit[i] = X[k]; f0 = I(); fit[i] = X[k-1]; f1 = I(); fit[i] = X[k-2]; f2 = I(); v0 = X[k-1] - X[k-2]; v1 = X[k ] - X[k-2]; v2 = X[k ] - X[k-1]; s0 = X[k-1]*X[k-1] - X[k-2]*X[k-2]; s1 = X[k ]*X[k ] - X[k-2]*X[k-2]; s2 = X[k ]*X[k ] - X[k-1]*X[k-1]; X[k+1] = 0.5*(f2*s2 - f1*s1 + f0*s0) / (f2*v2 - f1*v1 + f0*v0); k++; cout << k << " " << X[k] << endl; } fit[i] = X[k]; delete[]X; } void Methods :: Newton(int i) { D dt, T, It; int k=0; while(fabs(T-fit[i]) > 1e-3) { It = I(); T = fit[i]; fit[i] += 0.01; dt = I(); fit[i] -= 0.01; fit[i] -= It*0.001 / (dt - It); cout << k << " " << fit[i] << endl; k++; } } void Methods :: Cutters(int i) { D Tn, Tnm, Tnp, It, Itm; int j=0; Tn = 0.15; Tnm = 2.65;//otrezok Itm = I(); //cout << Tnm << " " << Tn << endl; while(fabs(Tn-Tnm) > 1e-6) { fit[i] = Tn; It = I(); Tnp = Tn - It * (Tn-Tnm) / (It-Itm); cout << j+1 << " " << Tnp << endl; Itm = It; Tnm = Tn; Tn = Tnp; j++; } fit[i] = Tnp; } void Methods :: Interval(D *ab, D st, int i) { D Fa, Fdx, d, c, Fb, fitbox = fit[i]; ab[0] = fit[i]; Fa = I(); fit[i] -= st; Fdx = I(); fit[i] += st; if(Fdx < Fa) st = -st; fit[i] += st; ab[1] = fit[i]; Fb = I(); while(Fb < Fa) { d = ab[0]; ab[0] = ab[1]; Fa = Fb; fit[i] += st; ab[1] = fit[i]; Fb = I(); cout << Fb << " " << Fa << endl; } if(st<0) { c = ab[1]; ab[1] = d; d = c; } ab[0] = d; fit[i] = fitbox; } void Methods :: Gold_section(int i) { D Fa, Fb, al, be; D *ab = new D[2]; D st = 0.5; D e = 0.5*(sqrt(5) - 1); Interval(ab, st, i); al = e*ab[0] + (1-e)*ab[1]; be = e*ab[1] + (1-e)*ab[0]; fit[i] = al; Fa = I(); fit[i] = be; Fb = I(); while(fabs(ab[1]-ab[0]) > e) { if(Fa < Fb) { ab[1] = be; be = al; Fb = Fa; al = e*ab[0] + (1-e)*ab[1]; fit[i] = al; Fa = I(); } if(Fa > Fb) { ab[0] = al; al = be; Fa = Fb; be = e*ab[1] + (1-e)*ab[0]; fit[i] = be; Fb = I(); } cout << ab[0] << " " << ab[1] << endl; } fit[i] = 0.5*(ab[0] + ab[1]); cout << ab[0] << " " << ab[1] << endl; } void Methods :: Grad(int N, D *g, D delta)//   { int n; D Fr, Fl, modG=0; for(n=0; n<N; n++) { fit[n] += delta; Fr = I(); fit[n] -= delta; fit[n] -= delta; Fl = I(); fit[n] += delta; g[n] = (Fr - Fl)*0.5/delta; modG += g[n]*g[n]; } modG = sqrt(modG); for(n=0; n<N; n++) g[n] /= modG; g[N] = I(); } void Methods :: ofGradient() { int n, j=0; D Fun, st, eps; const int N = 2; D *g = new D[N+1]; st = 0.1; eps = 0.000001; while(st > eps) { Grad(N,g,0.0001); for(n=0; n<N; n++) fit[n] -= st*g[n]; Fun = I(); if(Fun >= g[N]) { st /= 2.; for(n=0; n<N; n++) fit[n] += st*g[n]; } j++; cout << j << " " << fit[0]/ps << " " << fit[1]/ps << " " << fit[2]/ps<< endl; } } void Methods :: ofNelder_Mid() { int i, j, k; D modz = 0., p, eps = 1e-3; D FR, FN, F0, FE, FNm1, FC; const int N = 2; D *Co = new D[N]; D *Eo = new D[N]; D *Ro = new D[N]; D *Xo = new D[N]; D **Xx = new D*[N]; D **dz = new D*[N]; for(i=0;i<N;i++) { dz[i] = new D[N]; Xx[i] = new D[N+1]; } for(i=0;i<N;i++) for(j=0;j<N;j++) if(i^j) dz[i][j] = 0; else dz[i][j] = 1; for(i=0;i<N;i++) Xx[i][N] = fit[i]; for(i=0;i<N;i++) modz += fit[i]*fit[i]; modz = sqrt(modz); for(i=0;i<N;i++) dz[i][i] = 0.5*modz; for(i=0;i<N;i++) for(j=0;j<N;j++) Xx[i][j] = fit[i] + dz[i][j]; k = 0; p = Nor(Xx, N); while(p > eps) { k++; Srt(Xx, N); for(i=0;i<N;i++) Xo[i] = 0.; for(i=0;i<N;i++) for(j=0;j<N;j++) Xo[i] += Xx[i][j]; for(i=0;i<N;i++) Xo[i] /= N; for(i=0;i<N;i++) Ro[i] = Xo[i] + (Xo[i]-Xx[i][N]); for(i=0;i<N;i++) fit[i] = Ro[i]; FR = I(); for(i=0;i<N;i++) fit[i] = Xx[i][N]; FN = I(); if(FR > FN) { for(i=0;i<N;i++) for(j=1;j<=N;j++) Xx[i][j] = 0.5*(Xx[i][0] + Xx[i][j]); } else { for(i=0;i<N;i++) fit[i] = Xx[i][0]; F0 = I(); if(FR < F0) { for(i=0;i<N;i++) Eo[i] = Xo[i] +2*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Eo[i]; FE = I(); if(FE < FR) for(i=0;i<N;i++) Xx[i][N] = Eo[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } else { for(i=0;i<N;i++) fit[i] = Xx[i][N-1]; FNm1 = I(); if(FR <= FNm1) for(i=0;i<N;i++) Xx[i][N] = Ro[i]; else { for(i=0;i<N;i++) Co[i] = Xo[i] +0.5*(Xo[i] - Xx[i][N]); for(i=0;i<N;i++) fit[i] = Co[i]; FC = I(); if(FC < FR) for(i=0;i<N;i++) Xx[i][N] = Co[i]; else for(i=0;i<N;i++) Xx[i][N] = Ro[i]; } } } for(i=0;i<N;i++) cout << Xx[i][0] << " "; cout << k << " " << p << endl; p = Nor(Xx, N); if(p < eps) break; } for(i=0;i<N;i++) fit[i] = Xx[i][0]; /*for(i=0;i<N;i++) { for(j=0;j<N+1;j++) cout << Xx[i][j] << " "; cout << endl; }*/ delete[]Co; delete[]Xo; delete[]Ro; delete[]Eo; for(i=0;i<N;i++) { delete[]dz[i]; delete[]Xx[i]; } } //   D Methods :: Nor(D **X, int N) { int i, j, k; D norm, xij, pn = 0.; for(i=0;i<N;i++) for(j=i+1;j<=N;j++) { xij = 0.; for(k=0;k<N;k++) xij += ( (X[k][i]-X[k][j])*(X[k][i]-X[k][j]) ); pn = sqrt(xij);//    if(norm > pn) norm = pn;//   } return sqrt(norm); } //    void Methods :: Srt(D **X, int N) { int i, j, k; D temp; D *f = new D[N+1]; D *box = new D[N]; D **y = new D*[N+1]; for(i=0;i<N+1;i++)//  y[i] = new D[N+1]; for(i=0;i<N;i++) box[i] = fit[i];//    for(i=0;i<=N;i++) { for(j=0;j<N;j++) fit[j] = X[j][i]; f[i] = I();//     } for(i=0;i<N;i++) fit[i] = box[i];//    for(i=0;i<N;i++) for(j=0;j<=N;j++) y[i][j] = X[i][j]; for(i=0;i<=N;i++) y[N][i] = f[i];//stack(X, f) //    , //     N    for(i=1;i<=N;i++) for(j=0;j<=Ni;j++) if(y[N][j] >= y[N][j+1]) for(k=0;k<=N;k++) { temp = y[k][j]; y[k][j] = y[k][j+1]; y[k][j+1] = temp; } //submatrix   for(i=0;i<N;i++) for(j=0;j<=N;j++) X[i][j] = y[i][j]; /* for(i=0;i<=N;i++) { for(j=0;j<=N;j++) cout << y[i][j] << " "; cout << endl; } */ for(i=0;i<N+1;i++) delete[]y[i]; delete[]box; delete[]f; } int main() { Methods method; //method.ofDescent(); //method.ofGradient(); method.ofNelder_Mid(); return 0; } 

आज के लिए पर्याप्त है। अगला कदम वैश्विक अनुकूलन से कुछ का प्रयास करने के लिए तार्किक होगा, अधिक परीक्षण फ़ंक्शन टाइप करें, और फिर अंतर्निहित विधियों के साथ संकुल का अध्ययन करें।