स्टॉक मार्केट पर तकनीकी संकेतक वास्तव में कैसे काम करते हैं?

स्टॉक या क्रिप्टोकरेंसी में रुचि रखने वाले किसी भी व्यक्ति ने चार्ट पर इन अतिरिक्त लाइनों को देखा है। आपने राय सुनी होगी कि वे काम नहीं करते हैं। लेकिन वे महत्वपूर्ण डेटा का एक बहुत प्रदर्शन करते हुए, मेरी व्यापार क्षमता में सुधार करते हैं। लेकिन वे वास्तव में कैसे काम कर रहे हैं? और यह किसके लिए उपयोगी हो सकता है?

आपको इसे जरूर पढ़ना चाहिए:

1. आप दिन के कारोबार में उनका उपयोग करते हैं
2. आप एक ट्रेडिंग बॉट लिखने की योजना बना रहे हैं
3. यदि आप अपने द्वारा ट्रेडिंग रणनीति या संकेतक लागू करना चाहते हैं

अधिकांश अक्सर तकनीकी संकेतक एक विंडो फ़ंक्शन, पुनरावर्ती फ़ंक्शन या कीमतों / संस्करणों का भारित फ़ंक्शन होता है जो स्टॉक एक्सचेंज से UOHLCV प्रारूप (यूनिक्स समय, खुला, उच्च, निम्न, बंद, वॉल्यूम) में खींचा जाता है। संकेतकों के लिए बाद की गणना के आधार के रूप में विभिन्न फ़िल्टरिंग, न्यूनतम और मैक्सिमम या अन्य संकेतकों का उपयोग करना असामान्य नहीं है।

सरल चलती औसत (SMA)

जब संकेतक कोडिंग करते हैं, तो कार्यात्मक दृष्टिकोण का उपयोग करना बहुत सुविधाजनक है। उदाहरण के लिए, चलती औसत यह रोलिंग विंडो के प्रत्येक मूल्य का औसत है।

function sma($close, window) { return rolling(x => mean(x), window, $close); } 

जहां माध्य संचालन वह है जो सरणी के औसत की गणना करता है और रोलिंग विंडो फ़ंक्शन का संयोजन है जो कि सरणी में प्रत्येक मौजूदा तत्व के लिए अंतिम n तत्वों की एक सरणी का उत्पादन करता है और ऑपरेशन जो इस विंडो को एक नंबर में सिल देता है।

 function rolling(operation, window, array) { let result = []; for (let i = 0; i < array.length; i++) { if (i + 1 < window) { result.push(NaN); } else { result.push(operation(array.slice(i + 1 - window, i + 1))); } } return result; } 

एसएमए एक लैगिंग संकेतक है और प्रवृत्ति को निर्धारित करने में मदद करता है। यह चार्ट पर ओवरले के रूप में तैयार किया गया है और पहले मूल्यों को आमतौर पर खारिज कर दिया जाता है। क्रॉसओवर सिग्नल उत्पन्न करने के लिए दो मूविंग एवरेज का एक साथ उपयोग किया जा सकता है।



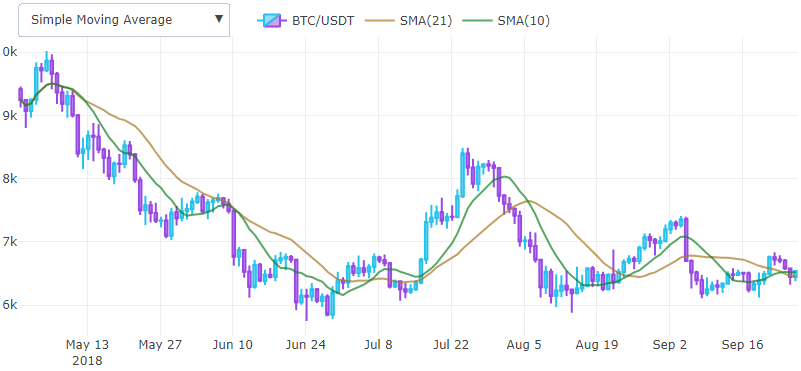
एक तेजी से क्रॉसओवर तब होता है जब एक अपेक्षाकृत कम चलती औसत ब्रेकआउट चलती औसत चलती है। अत्यधिक भारित चलती औसत का उपयोग अक्सर अभ्यास में किया जाता है, क्योंकि भारित विंडो फ़ंक्शन विलंब प्रभाव को कम करता है।

मानक विचलन (STDEV)

यदि हम एसएमए में औसत फ़ंक्शन को मानक विचलन के साथ बदलते हैं तो हमें एक स्लाइडिंग मानक विचलन मिलेगा

 function stdev($close, window) { return rolling(x => sd(x), window, $close); } 

जहां एसडी को विचरण के वर्गमूल के रूप में माना जाता है और आमतौर पर बेसेल सुधार के बिना। हम मानेंगे कि हर कोई समझता है कि एसडी को कैसे लागू किया जाए

$$

$$sd (x) = \ sqrt {\ frac {\ sum (x_i- \ hat x) ^ 2} [N]} $$$

विचरण के वर्गमूल का उपयोग किया जाता है क्योंकि विचरण ही आयाम सिद्धांत की अवधि में सुकारे डॉलर में मापा जाता है और इसलिए नहीं कि किसी ने ट्रेडमार्क या जो भी पंजीकृत किया है।

बोलिंगर बैंड (BBAND)

इस प्रकार हमने पहले ही दो बुनियादी संकेतक लागू कर दिए हैं जिन्हें हम जोड़ सकते हैं और नए प्राप्त कर सकते हैं। उदाहरण के लिए, यदि हम मूविंग एवरेज और स्टैंडर्ड डिविएशन को 2 से गुणा करने पर विचार करते हैं, तो हमें बोलिंगर बैंड का ऊपरी भाग और निचले हिस्से को हम घटाएंगे।

 function bb($close, window, mult) { let middle = sma($close, window); let upper = pointwise((a, b) => a + b * mult, middle, stdev($close, window)); let lower = pointwise((a, b) => a - b * mult, middle, stdev($close, window)); return { lower : lower, upper : upper}; } 

जहां फ़ंक्शन पॉइंटवाइज़ एक और उपयोगी कार्यात्मक है

 export function pointwise(operation, ...arrays) { let result = []; for (let i = 0, len = arrays[0].length; i < len; i++) { let iarr = (i) => arrays.map(x => x[i]); result[i] = operation(...iarr(i)); } return result; } 

और यह सिर्फ कई सरणियों के साथ ऑपरेशन करना है



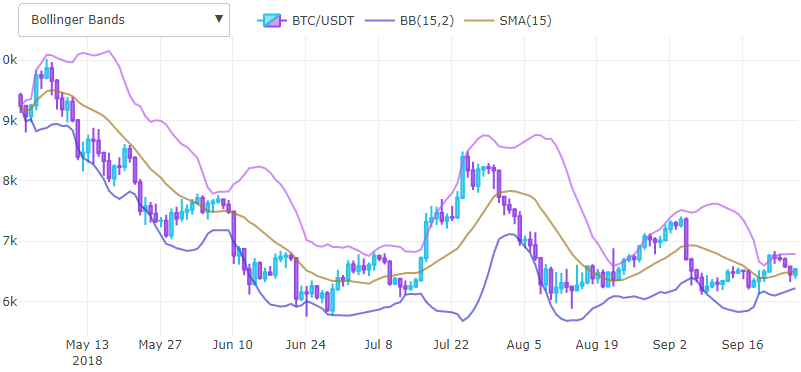
बोलिंजर बैंड बड़े मूल्य आंदोलन से पहले शांत को निर्धारित करने में मदद करते हैं, और चार्ट पर अधिकार अस्थिरता को विस्थापित करने के लिए एक उपकरण के रूप में उपयोग किया जाता है, मानक विचलन मूल्य से एक चार्ट पर ओवरले के रूप में प्रदर्शित होने के लिए चलती औसत से घटाया / जोड़ा जाता है।

घातीय मूविंग एवरेज (EMA)

हम साधारण चलती औसत के अंतराल को कैसे कम कर सकते हैं? चूंकि यह अंतिम n समापन कीमतों के माध्यम की गणना करता है इसलिए हम समझ सकते हैं कि हम कुछ वजन के साथ योग कर सकते हैं और पुरानी कीमतों के योगदान को कम कर सकते हैं।

$$

$$\ bar x = \ frac {\ sum x_i} {N} = \ frac {\ _ 1 \ _ cdot x_i} {\ sum 1} \ quad \ Rightarrow \ quad \ widetilde {x} = \ _rac {\ sum x_i w_i } {\ _ w_i}$$

उदाहरण के लिए यदि हम चुनते हैं $$$w_n = q ^ n$ और एक निरंतर $$$q$ यह एक से कम है, तो हमें एक असीम रूप से घटता हुआ वजन मिलता है, अगर हम कीमतों को नए सिरे से शुरू करेंगे।



यदि हम विंडो को पूर्ण लंबाई तक विस्तारित करते हैं और यह मानते हैं कि पूंछ का योगदान छोटा है, तो भी गणना की अनुमानित गणना और पुनरावर्ती समीकरण प्राप्त करना संभव है।

$$

$$1 + q + q ^ 2 + ... + q ^ n \ underset {n \ _ to \ infty} {\ underset {q <0} {=}} \ frac {1} {1-q} \\ \ _ mathrm {EMA} _ {curr} = \ frac {\ _ x_i q ^ i} {\ sum q ^ i} = ((1-q) \ sum x_i q ^ i \\ \ mathrm {EMA} {अगला} = \ frac {x_ {अगला} + q \ cdot \ sum x_i q ^ i} {1 + q \ cdot \ sum q ^ i} = ((1-q) \ cdot \ बाएँ [x_ {अगला} + q \ _dot \ _ योग x_i q ^ i \ right] \\ \ mathrm {EMA} _ {अगला} = (1-q) \ cdot x_ {अगला} + q) \ cdot \ mathrm {EMA} _ {वक्र}$$

Finnally हमें स्मूथिंग स्थिरांक के रूप में कुछ मान α = 1 - q चाहिए। यह प्रमाणित करना संभव है कि जब हम चुनते हैं $$$\ अल्फा = 2 / (एन + 1)$ ऊपर ईएमए और एसएमए वजन चार्ट के द्रव्यमान का केंद्र बराबर हो जाता है। कोड में यह बहुत अधिक सरल लगता है।

 function ema($close, window, weight = null) { weight = weight ? weight : 2 / (window + 1); let ema = [ mean($close.slice(0, window)) ]; for (let i = 1; i < $close.length; i++) { ema.push($close[i] * weight + ema[i - 1] * (1 - weight)); }; return ema; } 

सामान्य तौर पर यह समान चलती औसत लेकिन अधिक संवेदनशील होती है।


उपयोग की प्रभावशीलता वह आपके अनुभव और प्रयुक्त सेटिंग्स पर निर्भर करती है। इस साइट पर उदाहरण के लिए मापदंडों को बहुत अच्छी तरह से चुना जाता है।

चलती औसत अभिसरण विचलन (एमएसीडी)

1979 में जेराल्ड अपेल एक सबसे सरल और सबसे प्रभावी संकेतक उपलब्ध था। यह दो प्रवृत्ति ईएमए संकेतकों को एक गति थरथरानवाला में बदल देता है और दोनों दुनिया के सर्वश्रेष्ठ प्रदान करता है: निम्नलिखित प्रवृत्ति और गति। मोटे तौर पर एमएसीडी हिस्टोग्राम बोलना यह कीमत का एक व्युत्पन्न है। यह एक ओवरले के बजाय एक नई समन्वित प्रणाली में तैयार किया गया है और यह दो लाइनों और एक हिस्टोग्राम के साथ प्रतिनिधित्व करता है।



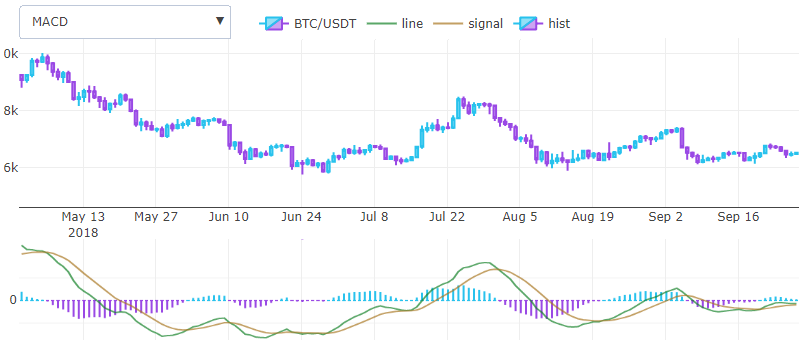
एमएसीडी लाइन की गणना करने के लिए हमें लंबे ईएमए को संक्षेप में बदलने की आवश्यकता है, बस। छोटी खिड़की के साथ इस लाइन का एक और ईएमए सिग्नल लाइन का उत्पादन करेगा। पिछले दो परिणामों के बीच अंतर करके हिस्टोग्राम प्राप्त किया जाता है।

 function macd($close, wshort, wlong, wsig) { let line = pointwise((a, b) => a - b, ema($close, wshort), ema($close, wlong)); let signal = ema(line, wsig); let hist = pointwise((a, b) => a - b, line, signal); return { line : line, signal : signal, hist : hist }; } 

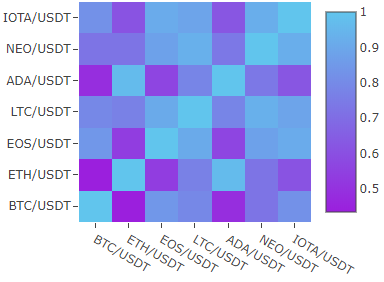
सहसंबंध मैट्रिक्स

यदि आप दीर्घकालिक निवेश और पोर्टफोलियो विश्लेषण में दखल देते हैं तो आप सहसंबंध मैट्रिक्स को उपयोगी पाएंगे।

 function cor(f, g) { let Ef = mean(f), Eg = mean(g); let Ef2 = mean(pointwise((a) => a * a, f)); let Eg2 = mean(pointwise((a) => a * a, g)); let Efg = mean(pointwise((a, b) => a * b, f, g)); return (Efg - Ef * Eg) / Math.sqrt((Ef2 - Ef * Ef) * (Eg2 - Eg * Eg)); } 

यहां 2 महीने में विभिन्न क्रिप्टोकरेंसी का सहसंबंध मैट्रिक्स है।

संकेतक इकाई परीक्षण

यदि हमारे पास संकेतक मानों की सटीक तालिकाएँ हैं, तो हम अपनी गणना का सटीक परीक्षण कर सकते हैं। दो कार्यों के बीच त्रुटि के माप का निर्धारण करने के विभिन्न तरीके हैं लेकिन इस मामले में सामान्यीकृत माध्य वर्ग त्रुटि बेहतर फिट है क्योंकि यह आरएमएसई के विपरीत आयाम रहित मात्रा है और यह सापेक्ष है।

$$

$$\ mathrm {NRMSE} = \ left। \ sqrt {\ frac {\ _ sum (\ hat x_i - x_i) ^ 2} {N}} \ Middle / (\ max {x_i} - \ min {x_i}) \ _ $$$

उदाहरण के लिए, बिटकॉइन की कीमत $ 20,000 हो सकती है और $ 10 का अंतर छोटा होता है, जबकि जब पूरे altcoin की कीमत $ 1 हो सकती है और $ 10 का अंतर बहुत बड़ा होता है।

 function nrmse(f, g) { let sqrDiff = pointwise((a, b) => (a - b) * (a - b), f, g); return Math.sqrt(mean(sqrDiff)) / (Math.max(...f) - Math.min(...f)); } 

हम एमएपीई का उपयोग भी कर सकते हैं लेकिन यह कम्यूटेटिव नहीं है और शून्य के पास समस्या है।

निष्कर्ष

तो यह बात है। कोड की कुछ पंक्तियों में हम बुनियादी तकनीकी संकेतकों को व्यक्त कर सकते हैं, अगर आपको यह पसंद है तो मेरे पुस्तकालय को जीथब पर चेक करें। वहां आप बहुत अधिक पा सकते हैं। यदि आप अपने बॉट चेक ज़िग-ज़ैग इंडिकेटर के लिए कुछ मशीन लर्निंग एल्गोरिदम का उपयोग करना चाहते हैं, तो प्रवेश बिंदु के रूप में।

संदर्भ

1. स्टॉकचार्ट्स - तालिकाओं में परीक्षण डेटा के साथ एल्गोरिदम की एक सूची।
2. क्रिप्टोवैच - संकेतकों के अच्छी तरह से ट्यून किए गए पैरामीटर।
3. गितुब - मेरा स्रोत कोड।

PS यदि आपको पाठ में कोई त्रुटि मिलती है तो कृपया मुझे सीधे बताएं।