जूलिया और कणों का झुंड

हम बहुआयामी अनुकूलन के तरीकों का अध्ययन करना जारी रखते हैं , और अगली पंक्ति में कण झुंड विधि है, जो वैश्विक न्यूनतम खोज करता है।

सिद्धांत

• विकिपीडिया
• विभिन्न कण झुंड के तरीके और उनकी टोपोलॉजी
• पायथन और C # में कणों का एक झुंड
• सील के एक पैक का अनुकूलन विधि

एल्गोरिथ्म बहुत सरल है:

एक निश्चित समय पर प्रत्येक कण की स्थिति की गणना सूत्र द्वारा की जाती है:

जहाँ $$$p_i$- एक विशेष कण के लिए सबसे अच्छा समाधान का समन्वय, $$$g_i$- इस युग के लिए सभी कणों के लिए सबसे अच्छा समाधान का समन्वय, $$$C_p$और $$$C_g$- वजन कारक (एक विशिष्ट मॉडल के लिए चयनित), $$$A_c$जड़ता का गुणांक है, इसे एक युग की संख्या पर निर्भर किया जा सकता है, फिर कण वेग आसानी से बदल जाएगा।

परीक्षण कार्य

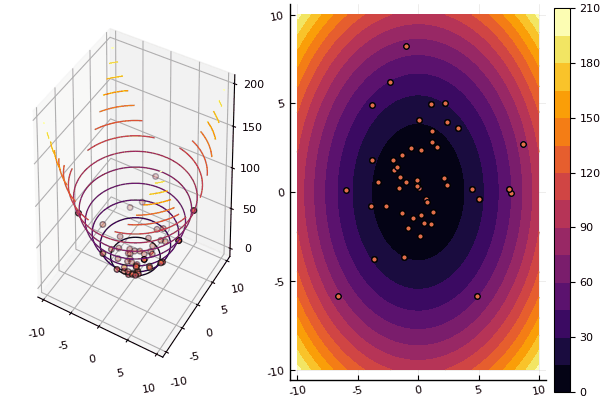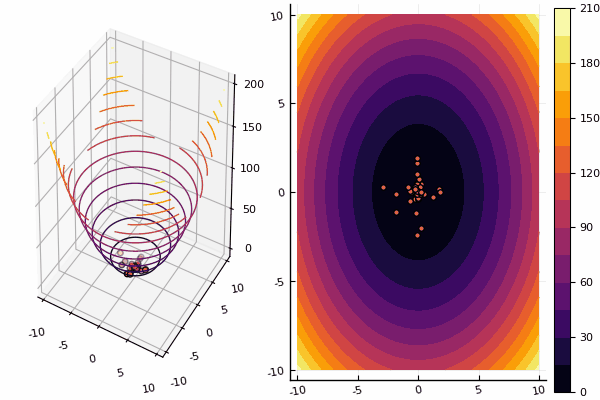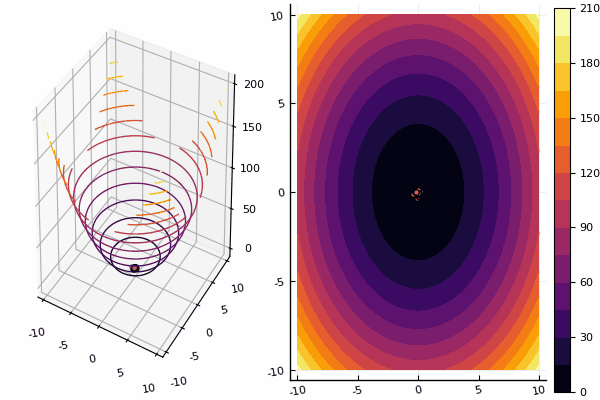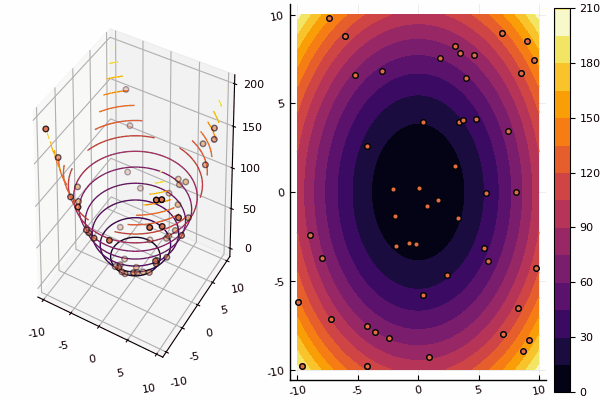
चूंकि विधि के काम को देखना बहुत अच्छा है, इसलिए हमें अधिक परीक्षण कार्य करने होंगे:

parabol(x) = sum(u->u*u, x) # f(0,0) = 0, x_i ∈ [-10,10] shvefel(x) = sum(u-> -u*sin(sqrt(abs(u))), x) # f(420.9687,420.9687) = -819?, x_i ∈ [-500,500] rastrigin(x) = 10*length(x) + sum(u->u*u-10*cos(2*pi*u), x) # f(0,0) = 0, x_i ∈ [-5,5] ekly(x) = -20exp(-0.2sqrt(0.5(x[1]*x[1]+x[2]*x[2]))) - exp(0.5(cospi(2x[1])+cospi(2x[2]))) + 20 + ℯ # f(0,0) = 0, x_i ∈ [-5,5] rosenbrok(x) = 100(x[2]-x[1]*x[1])^2 + (x[1]-1)^2 # f(0,0) = 0, x_i ∈ [-5,5] bill(x) = (1.5-x[1]+x[1]*x[2])^2 + (2.25-x[1]+x[1]*x[2]*x[2])^2 + (2.625-x[1]+x[1]*x[2]^3)^2 # f(3,0.5) = 0, x_i ∈ [-5,5] boot(x) = (x[1]+2x[2]-7)^2 + (2x[1]+x[2]-5)^2 # f(1,3) = 0, x_i ∈ [-10,10] bukin6(x) = 100sqrt(abs(x[2]-0.01x[1]*x[1])) + 0.01abs(x[1]+10) # f(-10,1) = 0, x_i ∈ [-15,-5; -3,3] levy13(x) = sinpi(3x[1])^2 + (1+sinpi(3x[2])^2)*(x[1]-1)^2 + (1+sinpi(2x[2])^2)*(x[2]-1)^2 # f(1,1) = 0, x_i ∈ [-10,10] himmelblau(x) = (x[1]^2+x[2]-11)^2 + (x[1]+x[2]^2-7)^2 # f(3,2)... = 0, x_i ∈ [-5,5] camel3humped(x) = 2x[1]^2 - 1.05x[1]^4 + x[1]^6 /6 + x[1]*x[2] + x[2]^2 # f(0,0) = 0, x_i ∈ [-5,5] izom(x) = -cos(x[1])*cos(x[2])*exp(-( (x[1]-pi)^2 + (x[2]-pi)^2 )) # f(π,π) = -1, x_i ∈ [-100,100] holdertable(x) = -abs(sin(x[1])*cos(x[2])exp(abs( 1-sqrt(x[1]^2+x[2]^2)/pi ))) # f(±8.05502,±9.66459) = -19.2085, x_i ∈ [-10,10] shaffer4(x) = 0.5 + (cos(sin(abs(x[1]^2-x[2]^2)))^2-0.5) / (1+0.001(x[1]^2+x[2]^2))^2 # f(0,1.25313) = 0.292579, x_i ∈ [-100,100] 

और, वास्तव में, स्वयं MRC:

 function mdpso(; nparts = 50, ndimes = 2, ages = 50, #   lover = [-10 -10], upper = [10 10], C1 = [1.9 1.9], #  - C2 = [1.8 1.8], Ac = [0.1 0.1], ) minind = 0 V = zeros(nparts,ndimes) #   n  n X = zeros(nparts,ndimes) funmin = -Inf Fmin = Inf Fbest = fill(Fmin, nparts) funx = zeros(nparts) xmem = zeros(nparts,ndimes) xbest = zeros(ndimes) #   #      for i in 1:nparts, j in 1:ndimes X[i,j] = randomer(lover[j], upper[j]) end for i in 1:ages for j in 1:nparts funx[j] = fun(X[j,:]) if funx[j] < Fbest[j] Fbest[j] = funx[j] xmem[j,:] = X[j,:] end end #      ploter(lover, upper, X, funx, i); funmin = minimum(funx) minind = argmin(funx) if funmin < Fmin Fmin = funmin xbest[:] = X[minind,:] end for j in 1:nparts, k in 1:ndimes R1 = rand() R2 = rand() V[j,k] = Ac[k]*V[j,k] + C1[k]*R1*(xmem[j,k] - X[j,k]) + C2[k]*R2*(xbest[k] - X[j,k]) X[j,k] += V[j,k] end println("Age № $i\n xbest:\n $(xbest[1]) $(xbest[2])") println("Fmin: $Fmin\n") end f = open("$fun.txt","w") #      write(f,"C1 = $C1, C2 = $C2, Ac = $Ac, lower = $lover, upper = $upper, ages = $ages, parts = $nparts") close(f) end 

आरेखण के साथ, हालांकि, गणना में अधिक समय लगता है, लेकिन यह पूर्ववर्ती है:

 using Plots pyplot() function ploter(l, u, xy, z, n_age ) contour(Xs, Ys, Zs, fill = true); #    (   ) #   ,       scatter!(xy[:,1], xy[:,2], legend = false, xaxis=( (l[1], u[1])), yaxis=( (l[2], u[2])) ); #savefig("$fun $n_age.png") #        end fun = bill low = [-4 -4] up = [4 4] Xs = range(low[1], stop = up[1], length = 80) Ys = range(low[2], stop = up[2], length = 80) Zs = [ fun([xy]) for y in Ys, x in Xs ] surface(Xs, Ys, Zs) xaxis!( (low[1], up[1]), low[1]:(up[1]-low[1])/5:up[1] ) yaxis!( (low[2], up[2]), low[2]:(up[2]-low[2])/5:up[2] ) 

 mdpso(C1 = [1.2 1.2], C2 = [1.1 1.1], Ac = [0.08 0.08], lower = [-4 -4], upper = [4 4], ages = 30) 

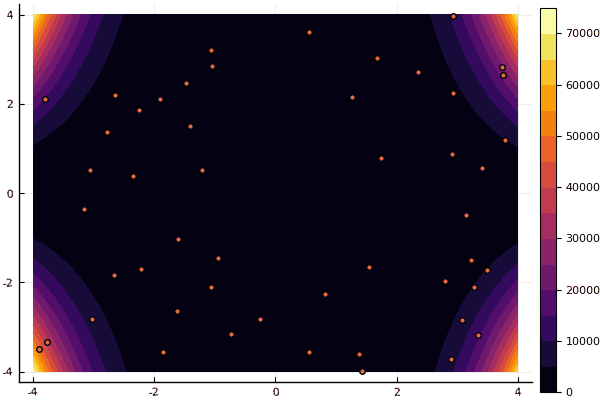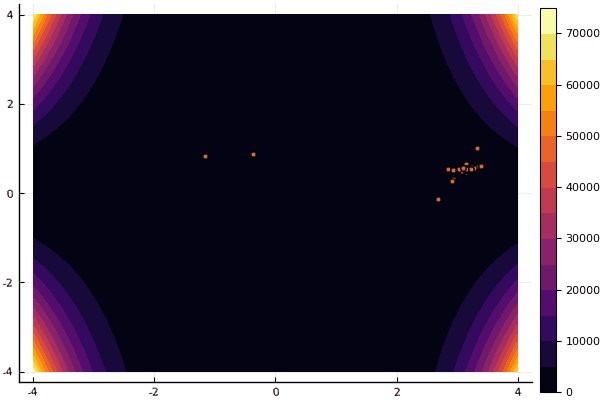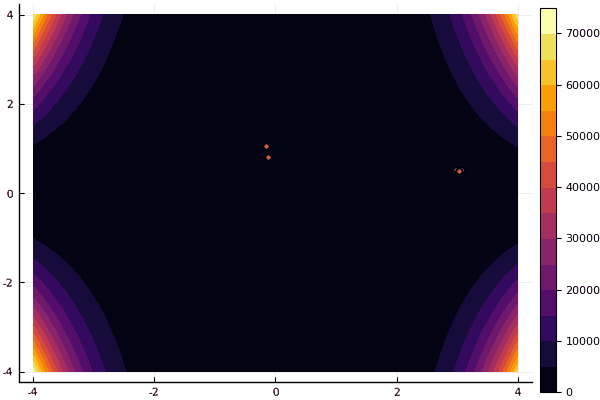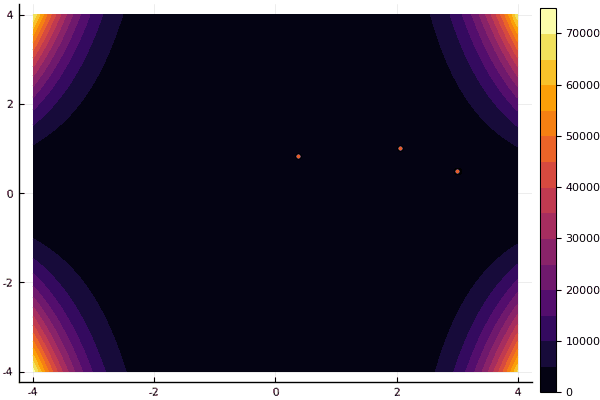
 fun = ekly mdpso(C1 = [1.7 1.7], C2 = [1.7 1.7], Ac = [0.07 0.07], lower = [-5 -5], upper = [5 5], ages = 15) 

 fun = himmelblau mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-5 -5], upper = [5 5], ages = 20, parts = 50) 

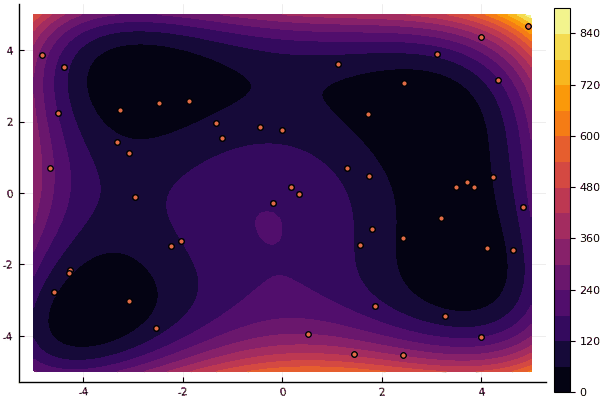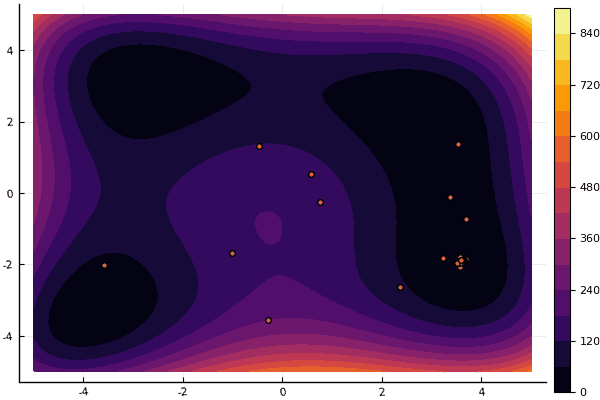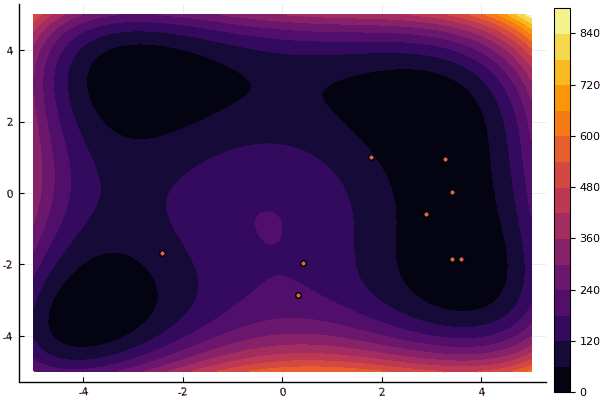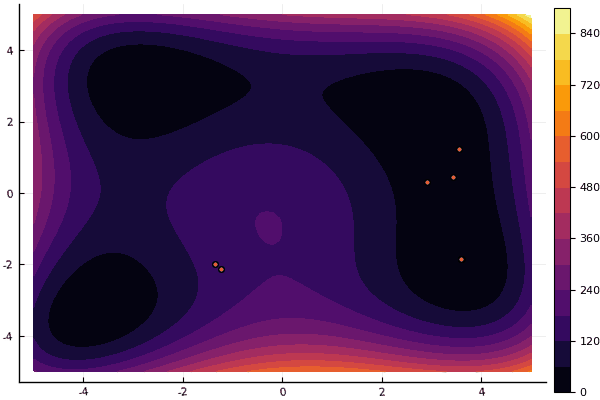
 fun = holdertable mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

 fun = levy13 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-10 -10], upper = [10 10], ages = 20, parts = 50) 

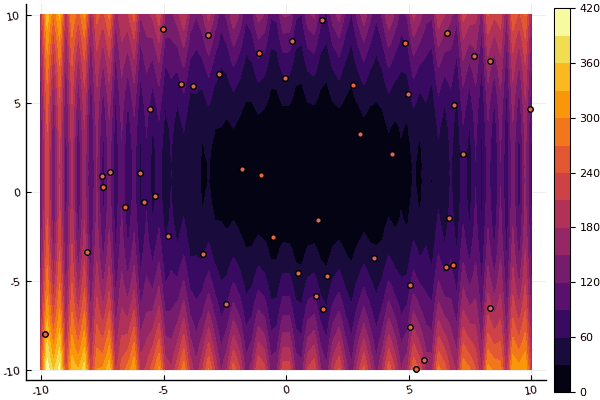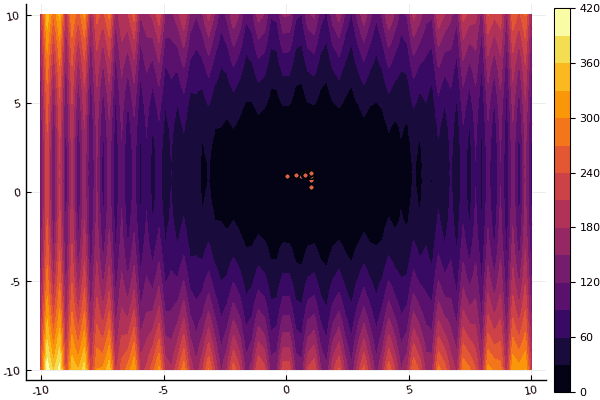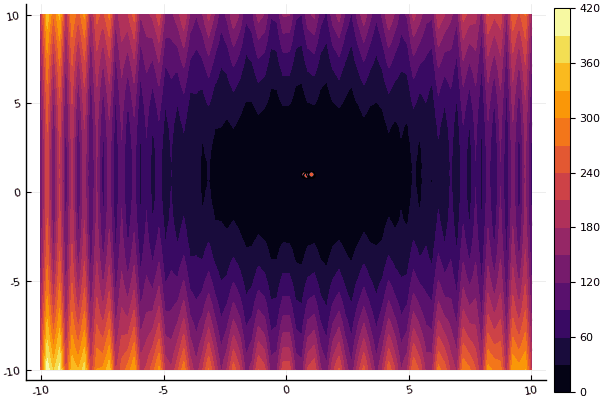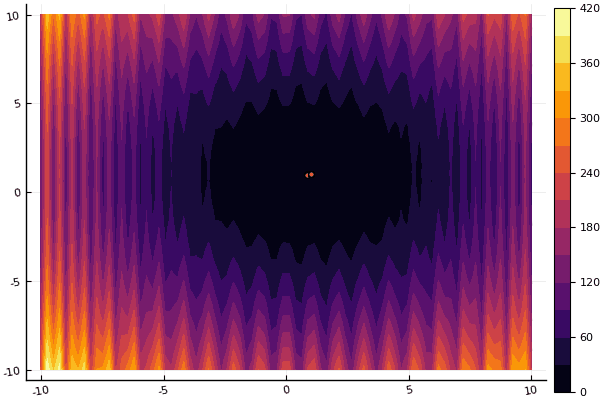
 fun = shaffer4 mdpso(C1 = [1.1 1.1], C2 = [1.0 1.0], Ac = [0.09 0.09], lower = [-100 -100], upper = [100 100], ages = 20, parts = 50) 

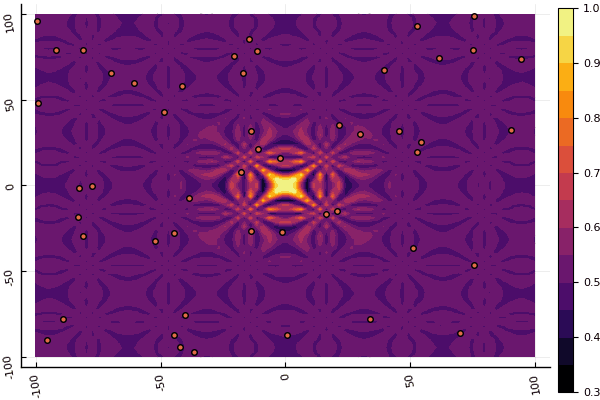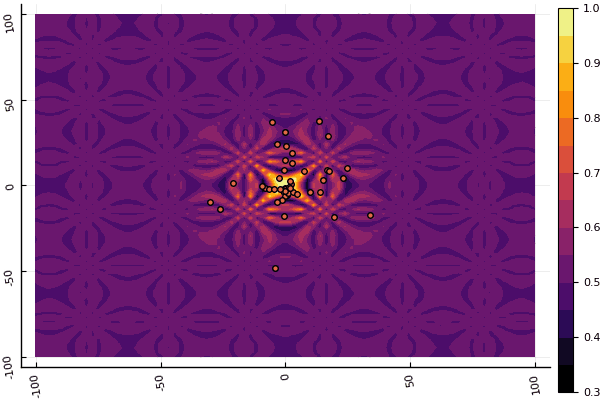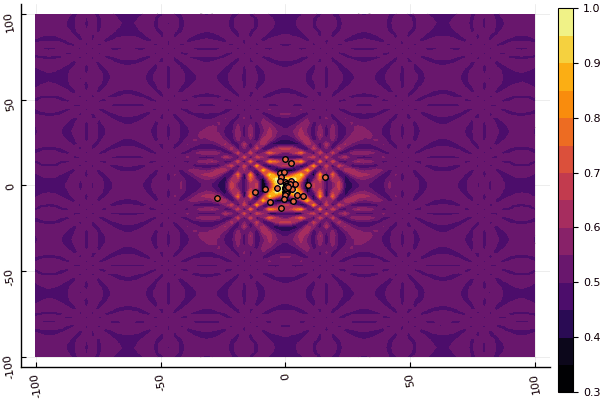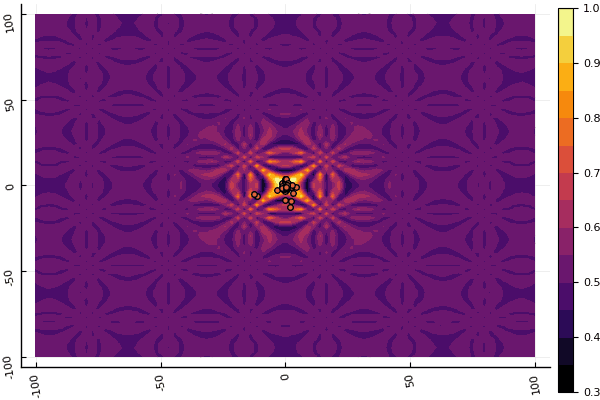
क्या वास्तव में डिप्रेशन मापदंडों और यादृच्छिकता के एक तत्व के साथ उपद्रव कर रहा है: यदि वैश्विक न्यूनतम के पास एक कण नहीं उड़ता है, तो यह पूरी चीज स्थानीय में गिर सकती है:

 fun = rastrigin mdpso(mdpso(C1 = [0.1 0.1], C2 = [1 1], Ac = [0.08 0.08], lover = low, upper = up, ages = 30)) 

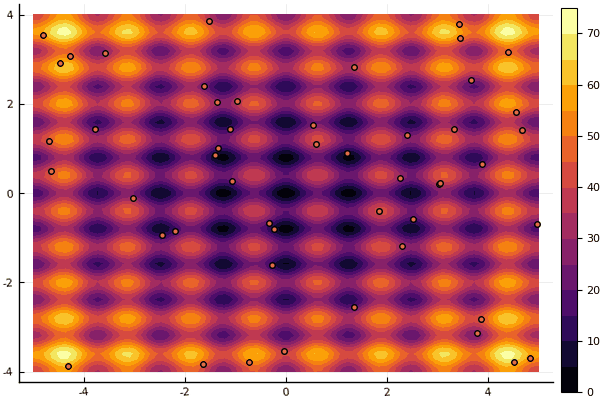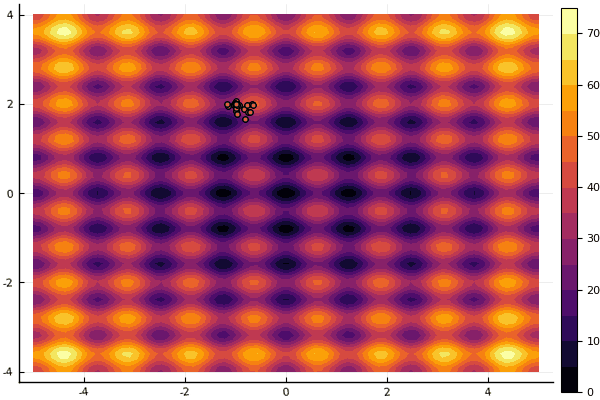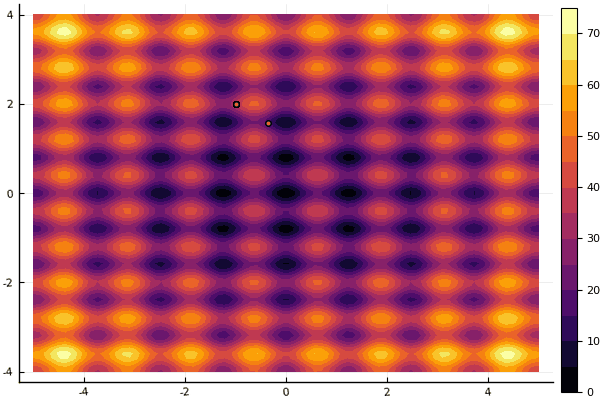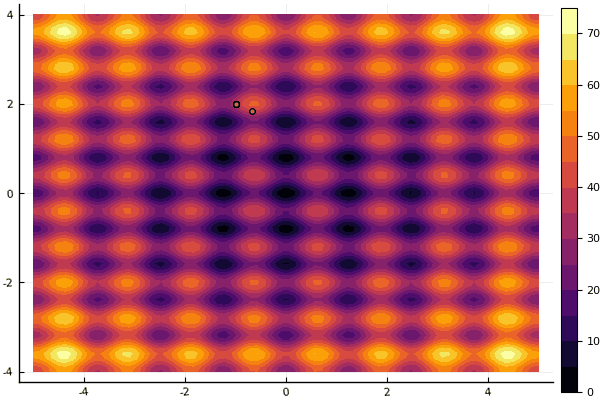
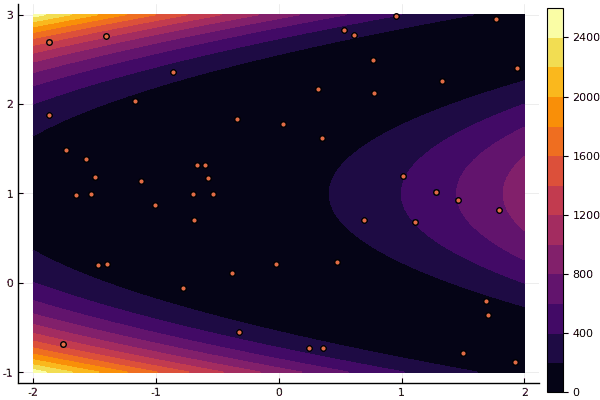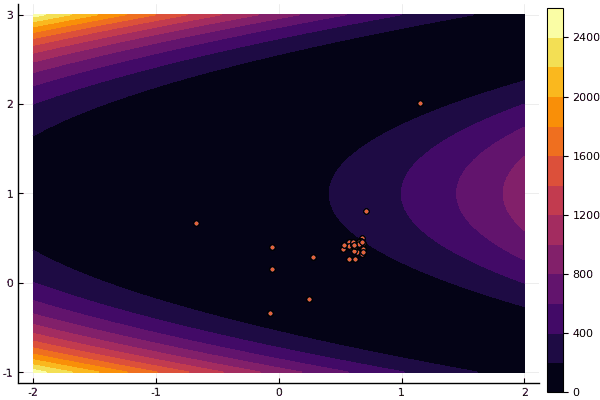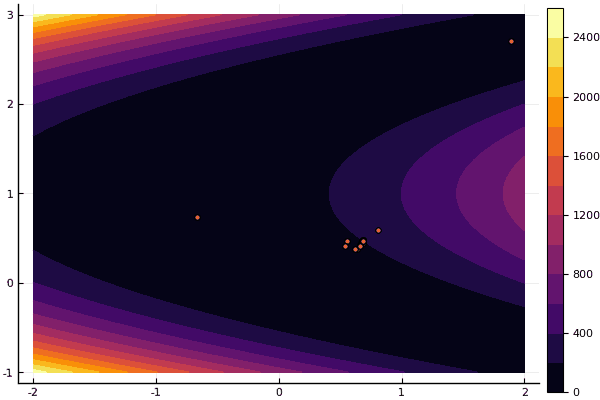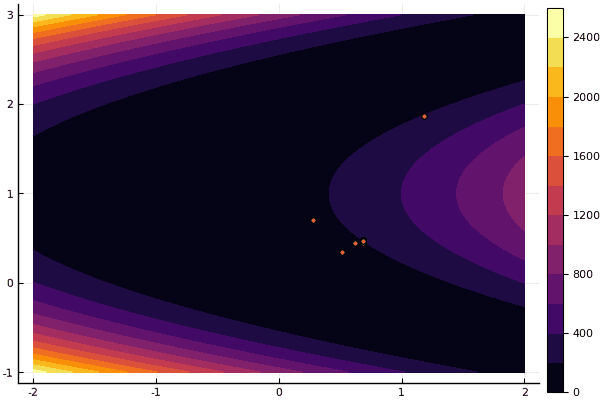
हाँ, और पुराना बहुत नहीं अच्छा रोसेनब्रोक अभी भी खुद को समझने की अनुमति नहीं देता है:

 fun = rosenbrok mdpso(C1 = [1.7 1.7], C2 = [1.5 1.5], Ac = [0.15 0.15], lover = low, upper = up, ages = 20, nparts = 50) ... Age № 20 xbest: 0.37796421341886866 0.12799160066705667 Fmin: 0.409026370833564 

लेकिन जैसा कि मैंने पहले कहा था, आप वैश्विक न्यूनतम के लिए एक अच्छे सन्निकटन की खोज के लिए FDM का उपयोग कर सकते हैं, और फिर निर्दिष्ट कर सकते हैं, कह सकते हैं, Nelder-Mead:

 vecl(x) = sqrt( sum(u -> u*u, x) ) function sortcoord(Mx) N = size(Mx,2) f = [fun(Mx[:,i]) for i in 1:N] #     Mx[:, sortperm(f)] end function normx(Mx) m = size(Mx,2) D = zeros(m-1,m) for i = 1:m, j = i+1:m D[i,j] = vecl(Mx[:,i] - Mx[:,j]) #     end D sqrt(maximum(D)) end function ofNelderMid(; ndimes = 2, ε = 1e-4, fit = [.1, .1], low = [-1 -1], up = [1 1]) k = 0 N = ndimes Xx = zeros(N, N+1) for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end p = normx(Xx) while p > ε k += 1 Xx = sortcoord(Xx) Xo = [ sum(Xx[i,1:N])/N for i = 1:N ] #  - i-  Ro = 2Xo - Xx[:,N+1] FR = fun(Ro) if FR > fun(Xx[:,N+1]) for i = 2:N+1 Xx[:,i] = 0.5(Xx[:,1] + Xx[:,i]) end else if FR < fun(Xx[:,1]) Eo = Xo + 2(Xo - Xx[:,N+1]) if FR > fun(Eo) Xx[:,N+1] = Eo else Xx[:,N+1] = Ro end else if FR <= fun(Xx[:,N]) Xx[:,N+1] = Ro else Co = Xo + 0.5(Xo - Xx[:,N+1]) if FR > fun(Co) Xx[:,N+1] = Co else Xx[:,N+1] = Ro end end end end println(k, " ", p, " ", Xx[:,1]) p = normx(Xx) end #while fit = Xx[:,1] end 

 ofNelderMid(fit = [0.37796 0.127992]) ... 92 0.00022610400555036366 [1.0, 1.0] 93 0.00015987967588703512 [1.0, 1.0] 94 0.00011305200343052599 [1.0, 1.0] 2-element Array{Float64,1}: 0.9999999996645973 0.9999999995466575 

शास्त्रीय एमएफसी के लिए, सब कुछ रोक मापदंड के साथ स्पष्ट नहीं है: सबसे अच्छा बिंदु कई युगों की स्थिति को पकड़ सकता है, कुछ कणों के बीच की दूरी भी लंबे समय तक नहीं बदल सकती है। इसलिए, युगों की संख्या पर एक सीमा का उपयोग किया जाता है। वैश्विक न्यूनतम खोजने की संभावनाओं को बढ़ाने के लिए, कणों और युगों की संख्या में वृद्धि करना आवश्यक है, जो स्मृति और, इसके अलावा, समय (कोई मज़ाक नहीं, प्रत्येक पुनरावृत्ति पर प्रत्येक आयाम के लिए उद्देश्य फ़ंक्शन की 50 कॉल) के मामले में बहुत महंगा है।

नैतिकता

• यदि आप जटिल और आधुनिक तरीकों का उपयोग नहीं करना चाहते हैं या नहीं कर सकते हैं, तो आप सरल विधि रचनाओं का उपयोग कर सकते हैं
• अक्सर एक समस्या के लिए एक संकीर्ण रूप से तीक्ष्ण विधि होती है (उदाहरण के लिए, खारा कार्यों के लिए)
• लगातार तुलना के लिए हाथ पर कई अलग-अलग एमओ होने की सलाह दी जाती है।
• अपने कार्य को विधि में रखना और सही उत्तर प्राप्त करना हमेशा संभव नहीं होता है - आपको शोध में समय व्यतीत करना चाहिए, मापदंडों को अलग करना चाहिए, यदि आप राहत नहीं देख सकते हैं, तो आपको अभिसरण को ट्रैक करने के लिए कम से कम मध्यवर्ती गणना का प्रिंट आउट लेना चाहिए।

आज के लिए बस इतना ही, आपके ध्यान के लिए धन्यवाद और आप सभी को एक अच्छा अनुकूलन चाहिए!