🚫 👩🏼‍🎓 🍝 जूलिया और अनुकूलन 💦 🧛🏻 🥄

यह उन पैकेजों पर विचार करने का समय है जो अनुकूलन समस्याओं को हल करने के लिए तरीके प्रदान करते हैं। कुछ फ़ंक्शन के न्यूनतम को खोजने के लिए बहुत सारी समस्याओं को कम किया जा सकता है, इसलिए आपके पास शस्त्रागार में एक या दो सॉल्वर होने चाहिए, और यहां तक कि पूरे पैकेज भी।

प्रविष्टि

जूलिया भाषा लोकप्रियता हासिल करना जारी रखती है । Https://juliacomputing.com पर आप देख सकते हैं कि खगोलविद, रोबोटिक्स और फाइनेंसर इस भाषा को क्यों चुनते हैं, और https://academy.juliabox.com पर आप भाषा सीखने और किसी भी तरह की मशीन सीखने में इसका उपयोग करने के लिए मुफ्त पाठ्यक्रम शुरू कर सकते हैं। उन लोगों के लिए जिन्होंने गंभीरता से सीखना शुरू करने का फैसला किया है, मैं आपको वीडियो देखने, लेख पढ़ने और https://julialang.org/learning/ पर बृहस्पति लैपटॉप पर क्लिक करने या कम से कम ऊपर से हब के माध्यम से जाने की सलाह देता हूं: स्थापना, और सुविधाएँ, और व्यवसाय के लिए आवेदन होगा। तत्काल। अब पुस्तकालयों के लिए नीचे उतरो।

BlackBoxOptim

BlackBoxOptim - जूलिया के लिए वैश्विक अनुकूलन पैकेज ( http://julialang.org/ )। यह दोनों बहुउद्देश्यीय और एकल-उद्देश्य अनुकूलन समस्याओं का समर्थन करता है और (मेटा) हेयुरिस्टिक / स्टोचस्टिक एल्गोरिदम (डीई, एनईएस, आदि) पर केंद्रित है जो अधिक पारंपरिक, नियतात्मक एल्गोरिदम के विपरीत, अनुकूलित फ़ंक्शन को अलग-अलग होने की आवश्यकता नहीं है, जो अक्सर ग्रेडिएंट / भिन्नता पर आधारित होते हैं। यह धीरे-धीरे मूल्यांकन किए जाने वाले कार्यों के अनुकूलन को गति देने के लिए समानांतर कंप्यूटिंग का भी समर्थन करता है।

लाइब्रेरी को डाउनलोड करें और कनेक्ट करें

]add BlackBoxOptim using BlackBoxOptim

Rosenbrock फ़ंक्शन सेट करें:

 f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2

हम दो-आयामी समस्या के लिए प्रत्येक समन्वय के लिए अंतराल (-5; 5) पर एक न्यूनतम की तलाश कर रहे हैं:

 res = bboptimize(f; SearchRange = (-5.0, 5.0), NumDimensions = 2)

उत्तर क्या होगा:

 Starting optimization with optimizer DiffEvoOpt{FitPopulation{Float64},RadiusLimitedSelector,BlackBoxOptim.AdaptiveDiffEvoRandBin{3},RandomBound{RangePerDimSearchSpace}} 0.00 secs, 0 evals, 0 steps Optimization stopped after 10001 steps and 0.12400007247924805 seconds Termination reason: Max number of steps (10000) reached Steps per second = 80653.17866385692 Function evals per second = 81628.98454510146 Improvements/step = 0.2087 Total function evaluations = 10122 Best candidate found: [1.0, 1.0] Fitness: 0.000000000

और बहुत सारे अपठनीय डेटा, लेकिन एक न्यूनतम पाया गया था। चूंकि स्टोचस्टिक का उपयोग किया जाता है, फ़ंक्शन कॉल थोड़ा अधिक होगा, इसलिए बहुआयामी कार्यों के लिए तरीकों के चयन का उपयोग करना बेहतर होता है

 function rosenbrock(x) return( sum( 100*( x[2:end] - x[1:end-1].^2 ).^2 + ( x[1:end-1] - 1 ).^2 ) ) end res = compare_optimizers(rosenbrock; SearchRange = (-5.0, 5.0), NumDimensions = 30, MaxTime = 3.0);

उत्तल

उत्तल जूलिया अनुशासित उत्तल प्रोग्रामिंग पैकेज (अनुशासनात्मक उत्तल प्रोग्रामिंग?) है। Convex.jl MathProgBase इंटरफ़ेस के माध्यम से रैखिक कार्यक्रमों, मिश्रित पूर्णांक रैखिक कार्यक्रमों और MCP, Gurobi, ECOS, SCS और GLPK सहित विभिन्न सॉल्वरों का उपयोग करते हुए DCP- संगत उत्तल कार्यक्रमों को हल कर सकता है। यह जटिल चर और गुणांक के साथ अनुकूलन का भी समर्थन करता है।

 using Pkg #      Pkg.add("Convex") Pkg.add("SCS")

साइट पर कई उदाहरण हैं: टोमोग्राफी (वितरण क्षेत्रों पर दिए गए इंटीग्रल द्वारा घनत्व वितरण को पुनर्स्थापित करने की प्रक्रिया। उदाहरण के लिए, आप टोमोग्राफी के साथ काले और सफेद चित्रों में काम कर सकते हैं), एन्ट्रापी, लॉजिस्टिक प्रतिगमन, रैखिक प्रोग्रामिंग, आदि को अधिकतम कर सकते हैं।

उदाहरण के लिए, आपको शर्तों को पूरा करने की आवश्यकता है:

\ शुरू {सरणी} {ll} \ mbox {संतुष्ट} और \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {सरणी}

$\ शुरू {सरणी} {ll} \ mbox {संतुष्ट} और \ | x \ | _2 \ leq 100 \\ & e ^ {x_1} \ leq 5 \\ & x_2 \ geq 7 \\ & \ sqrt {x_3 x_4} \ geq x_2 \ end {सरणी}$

 using Convex, SCS, LinearAlgebra x = Variable(4) p = satisfy(norm(x) <= 100, exp(x[1]) <= 5, x[2] >= 7, geomean(x[3], x[4]) >= x[2]) solve!(p, SCSSolver(verbose=0)) println(p.status) x.value

जवाब देंगे

 Optimal 4×1 Array{Float64,2}: 0.0 8.554892320716046 15.329934133156783 15.329934133156783

कूदना

JuMP एक डोमेन-विशिष्ट गणितीय अनुकूलन भाषा है जिसे जूलिया में बनाया गया है। वह वर्तमान में कई खुले और वाणिज्यिक सॉल्वर (आर्टलीज निटरो, बैरन, बोनमिन, सीबीपीसी, क्लीप, कौएने, सीपीओएस, ईसीओएस, फिको एक्सपे्रस, जीएलपीके, गुरोबी, इप्टॉप, मोस्को, एनएलओटीपी, एससीएस) का समर्थन करता है।

JuMP को विशेषज्ञ ज्ञान के बिना अनुकूलन समस्याओं की पहचान करना और हल करना आसान बनाता है, लेकिन साथ ही यह विशेषज्ञों को उन्नत एल्गोरिथम विधियों को लागू करने की अनुमति देता है, जैसे कि प्रभावी "हॉट" का उपयोग रेखीय प्रोग्रामिंग में शुरू होता है या कॉलबैक का उपयोग शाखा और सीमा सॉल्वर के साथ बातचीत करने के लिए होता है। JuMP भी तेज है - बेंचमार्किंग से पता चला है कि यह उच्च स्तर की सार्वभौमिक प्रोग्रामिंग भाषा की स्पष्टता को बनाए रखते हुए AMPL जैसे विशेष वाणिज्यिक उपकरणों के समान गति पर गणना को संभाल सकता है। JuMP को आसानी से जटिल वर्कफ़्लो में एकीकृत किया जा सकता है, जिसमें सिमुलेशन और वेब सर्वर शामिल हैं।

यह उपकरण आपको इस तरह के कार्यों से निपटने की अनुमति देता है:

एलपी = रैखिक प्रोग्रामिंग
QP = द्विघात प्रोग्रामिंग
SOCP = द्वितीय-क्रम शंक्वाकार प्रोग्रामिंग (उत्तल द्विघात बाधाओं और / या उद्देश्य के साथ समस्याओं सहित)
MILP = मिश्रित पूर्णांक रैखिक प्रोग्रामिंग
एनएलपी = नॉनलाइनियर प्रोग्रामिंग
MINLP = मिश्रित पूर्णांक nonlinear प्रोग्रामिंग
एसडीपी = अर्ध-परिभाषित प्रोग्रामिंग
MISDP = मिश्रित पूर्णांक अर्धवृत्ताकार प्रोग्रामिंग

इसकी क्षमताओं का विश्लेषण कई लेखों के लिए पर्याप्त होगा, इसलिए अभी के लिए निम्नलिखित पर चलते हैं:

Optim

ऑप्टिमाइज़ेशन दोनों मुफ्त और व्यावसायिक स्रोतों से उपलब्ध कई सॉल्वर हैं, और कई जूलिया में उपयोग के लिए पहले से ही लिपटे हुए हैं। उनमें से कुछ इस भाषा में लिखे गए हैं। प्रदर्शन के संदर्भ में, यह शायद ही कभी एक समस्या है, क्योंकि वे अक्सर फोरट्रान या सी में लिखे जाते हैं। हालांकि, जूलिया में सीधे लिखे गए सॉल्वर के कुछ फायदे हैं।

जब जूलिया सॉफ्टवेयर (पैकेज) लिखते हैं जिसके लिए कुछ अनुकूलित करने की आवश्यकता होती है, तो प्रोग्रामर या तो अपनी स्वयं की अनुकूलन प्रक्रिया लिख सकता है या उपलब्ध कई सॉल्वर में से एक का उपयोग कर सकता है। उदाहरण के लिए, यह NLOpt सेट से कुछ हो सकता है। इसका मतलब यह है कि एक निर्भरता को जोड़ना जो जूलिया में नहीं लिखा गया है, और आपको उस वातावरण के बारे में अधिक धारणा बनाने की आवश्यकता है जिसमें उपयोगकर्ता स्थित है। क्या उपयोगकर्ता के पास उचित संकलक हैं? क्या मैं किसी प्रोजेक्ट में GPL कोड का उपयोग कर सकता हूं?

यह भी सच है कि सी या फोरट्रान में लिखे एक सॉल्वर का उपयोग करना जूलिया के मुख्य लाभों में से एक का उपयोग करना असंभव बनाता है: एकाधिक प्रेषण। चूंकि ऑप्टिम पूरी तरह से जूलिया में लिखा गया है, इसलिए हम वर्तमान में कस्टम प्रेसेट्स का उपयोग करना आसान बनाने के लिए एक प्रेषण प्रणाली का उपयोग कर सकते हैं। इस दिशा में एक नियोजित सुविधा एल्गोरिदम के विभिन्न चरणों के लिए सॉल्वर के उपयोगकर्ता-चालित चयन की अनुमति देना है, जो पूरी तरह से ऑप्टिमाइज़ डेवलपर्स द्वारा चुनी गई पूर्वनिर्धारित क्षमताओं के बजाय प्रेषण पर आधारित है।

जूलिया पर एक पैकेज का अर्थ यह भी है कि ऑप्टिमाइज़ेशन के पास जूलियाडिफ़ में पैकेज के माध्यम से स्वचालित भेदभाव कार्यों तक पहुंच है।

नेतृत्व

आइए शुरू:

 ]add Optim using Optim #   f(x) = (1.0 - x[1])^2 + 100.0 * (x[2] - x[1]^2)^2 x0 = [0.0, 0.0] optimize(f, x0)

हमें एक सुविधाजनक रिपोर्ट के साथ एक उत्तर मिलता है:

 Results of Optimization Algorithm * Algorithm: Nelder-Mead #   * Starting Point: [0.0,0.0] * Minimizer: [0.9999634355313174,0.9999315506115275] * Minimum: 3.525527e-09 * Iterations: 60 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 118

और मेरे नेल्डर मीड के साथ तुलना करें!

स्पॉइलर

मेरा धीमी हो जाएगा :(

दूर ले जाया गया

 using BenchmarkTools @benchmark optimize(f, x0) BenchmarkTools.Trial: memory estimate: 11.00 KiB allocs estimate: 419 -------------- minimum time: 39.078 μs (0.00% GC) median time: 43.420 μs (0.00% GC) mean time: 53.024 μs (15.02% GC) maximum time: 59.992 ms (99.83% GC) -------------- samples: 10000 evals/sample: 1

चेक के दौरान, यह भी पता चला कि यदि आप प्रारंभिक सन्निकटन (0, 0) का उपयोग करते हैं तो मेरा कार्यान्वयन काम नहीं करता है। एक कसौटी मानदंड के रूप में, आप सिम्पलेक्स के आयतन का उपयोग कर सकते हैं, लेकिन मैं एक मैट्रिक्स के मानदंड का उपयोग करता हूं। यहां आप मानदंड की ज्यामितीय व्याख्या के बारे में पढ़ सकते हैं । दोनों मामलों में, शून्य का एक मैट्रिक्स प्राप्त किया जाता है - एक पतित मैट्रिक्स का एक विशेष मामला; इसलिए, विधि किसी भी चरण का प्रदर्शन नहीं करती है। आप एक प्रारंभिक सिम्प्लेक्स के निर्माण को कॉन्फ़िगर कर सकते हैं, उदाहरण के लिए, प्रारंभिक सन्निकटन से इसके कोने की दूरी निर्धारित करके (और मेरी तरह नहीं - वेक्टर की आधी लंबाई, फू, क्या शर्म की बात है ...), तो विधि सेटिंग अधिक लचीली होगी, या सुनिश्चित करें कि सभी कोने नहीं हैं। एक बिंदु पर बैठ गया:

  for i = 1:N+1 Xx[:,i] = fit end for i = 1:N Xx[i,i] += 0.5*vecl(fit) + ε end

ठीक है, मेरा सिंप्लेक्स गोराज़दो धीमा है:

 ofNelderMid(fit = [0, 0.]) step= 118 7.7234e-5 f = 2.797-18 x = [1.0, 1.0] @benchmark ofNelderMid(fit = [0., 0.]) BenchmarkTools.Trial: memory estimate: 394.03 KiB allocs estimate: 6632 -------------- minimum time: 717.221 μs (0.00% GC) median time: 769.325 μs (0.00% GC) mean time: 854.644 μs (5.04% GC) maximum time: 50.429 ms (98.01% GC) -------------- samples: 5826 evals/sample: 1

अब अध्ययन पैकेज पर लौटने का अधिक कारण

आप उपयोग की गई विधि चुन सकते हैं:

 optimize(f, x0, LBFGS()) Results of Optimization Algorithm * Algorithm: L-BFGS * Starting Point: [0.0,0.0] * Minimizer: [0.9999999926662504,0.9999999853325008] * Minimum: 5.378388e-17 * Iterations: 24 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 4.54e-11 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 5.30e-03 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 9.88e-14 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 67 * Gradient Calls: 67

और इसके लिए विस्तृत दस्तावेज और संदर्भ प्राप्त करें

 ?LBFGS()

आप याकूबियन और हेसियन फ़ंक्शन सेट कर सकते हैं

 function g!(G, x) G[1] = -2.0 * (1.0 - x[1]) - 400.0 * (x[2] - x[1]^2) * x[1] G[2] = 200.0 * (x[2] - x[1]^2) end function h!(H, x) H[1, 1] = 2.0 - 400.0 * x[2] + 1200.0 * x[1]^2 H[1, 2] = -400.0 * x[1] H[2, 1] = -400.0 * x[1] H[2, 2] = 200.0 end optimize(f, g!, h!, x0) Results of Optimization Algorithm * Algorithm: Newtons Method * Starting Point: [0.0,0.0] * Minimizer: [0.9999999999999994,0.9999999999999989] * Minimum: 3.081488e-31 * Iterations: 14 * Convergence: true * |x - x'| ≤ 0.0e+00: false |x - x'| = 3.06e-09 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: false |f(x) - f(x')| = 3.03e+13 |f(x)| * |g(x)| ≤ 1.0e-08: true |g(x)| = 1.11e-15 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 44 * Gradient Calls: 44 * Hessian Calls: 14

जाहिर है, स्वचालित रूप से न्यूटन विधि से काम किया। और इसलिए आप खोज क्षेत्र सेट कर सकते हैं और ढाल वंश का उपयोग कर सकते हैं:

 lower = [1.25, -2.1] upper = [Inf, Inf] initial_x = [2.0, 2.0] inner_optimizer = GradientDescent() results = optimize(f, g!, lower, upper, initial_x, Fminbox(inner_optimizer)) Results of Optimization Algorithm * Algorithm: Fminbox with Gradient Descent * Starting Point: [2.0,2.0] * Minimizer: [1.2500000000000002,1.5625000000000004] * Minimum: 6.250000e-02 * Iterations: 8 * Convergence: true * |x - x'| ≤ 0.0e+00: true |x - x'| = 0.00e+00 * |f(x) - f(x')| ≤ 0.0e+00 |f(x)|: true |f(x) - f(x')| = 0.00e+00 |f(x)| * |g(x)| ≤ 1.0e-08: false |g(x)| = 5.00e-01 * Stopped by an increasing objective: false * Reached Maximum Number of Iterations: false * Objective Calls: 84382 * Gradient Calls: 84382

खैर, या मैं नहीं जानता, मान लें कि आप समीकरण को हल करना चाहते थे

 f_univariate(x) = 2x^2+3x+1 optimize(f_univariate, -2.0, 1.0) Results of Optimization Algorithm * Algorithm: Brents Method * Search Interval: [-2.000000, 1.000000] * Minimizer: -7.500000e-01 * Minimum: -1.250000e-01 * Iterations: 7 * Convergence: max(|x - x_upper|, |x - x_lower|) <= 2*(1.5e-08*|x|+2.2e-16): true * Objective Function Calls: 8

और उसने तुम्हें ब्रेंट मेथड चुना।
या प्रयोगात्मक डेटा होने पर, आपको मॉडल गुणांक को अनुकूलित करने की आवश्यकता होती है

F (p_{1}, p_{2}, x) = p_{1} c o s (p_{2} x) + p_{2} s i n (p_{1} x)

$F (p_1, p_2, x) = p_1 \ cos (p_2x) + p_2 \ sin (p_1x)$

p_{1} = 1, p_{2} = 0.2

$p_1 = 1, p_2 = 0.2$

 F(p, x) = p[1]*cos(p[2]*x) + p[2]*sin(p[1]*x) model(p) = sum( [ (F(p, xdata[i]) - ydata[i])^2 for i = 1:length(xdata)] ) xdata = [-2,-1.64,-1.33,-0.7,0,0.45,1.2,1.64,2.32,2.9] ydata = [0.699369,0.700462,0.695354,1.03905,1.97389,2.41143,1.91091,0.919576,-0.730975,-1.42001] res2 = optimize(model, [1.0, 0.2]) Results of Optimization Algorithm * Algorithm: Nelder-Mead * Starting Point: [1.0,0.2] * Minimizer: [1.8818299027162517,0.7002244825046421] * Minimum: 5.381270e-02 * Iterations: 34 * Convergence: true * √(Σ(yᵢ-ȳ)²)/n < 1.0e-08: true * Reached Maximum Number of Iterations: false * Objective Calls: 71

 P = Optim.minimizer(res2) Y = [ F(P, x) for x in xdata] using Plots plotly() plot(xdata, ydata) plot!(xdata, Y)

बोनस। अपना परीक्षण कार्य बनाएं

विचार का उपयोग खाबरोव लेख से किया गया है । आप प्रत्येक स्थानीय न्यूनतम को स्वयं कॉन्फ़िगर कर सकते हैं:

 """ https://habr.com/ru/post/349660/ :param n:   :param a:    ,   ,    /      :param c:    :param p:       :param b:    :return:  ,       ,          """ function feldbaum(x; n=5, a=[3 2; 4 3; 2 1; 4 5; .5 .5], c=[-1 2; 2 1; -3 2; -2 -2; 1.5 -2], p=[9 6; 1 1; 1.5 1.4; 1.2 1.3; 0.5 0.5], b=[0 1 3.2 2 4.6]) l = zeros(n) for i = 1:n res = 0 for j = 1:size(x,1) res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

और आप सर्वशक्तिमान की इच्छा के लिए सब कुछ छोड़ सकते हैं

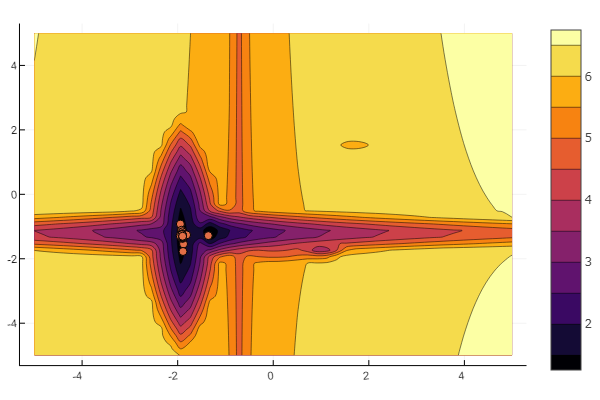
 n=10 m = 2 a = rand(0:0.1:6, n, m) c = rand(-2:0.1:2, n, m) p = rand(0:0.1:2, n, m) b = rand(0:0.1:8, n, m) function feldbaum(x) l = zeros(n) for i = 1:n res = 0 for j = 1:m res += a[i,j] * abs(x[j] - c[i,j]) ^ p[i,j] end res += b[i] l[i] = res end minimum(l) end

लेकिन जैसा कि आप शुरुआती तस्वीर से देख सकते हैं, इस तरह की राहत के साथ कणों का एक झुंड डराना नहीं है।

यह किया जाना चाहिए। जैसा कि आप देख सकते हैं, जूलिया में एक काफी शक्तिशाली और आधुनिक गणितीय वातावरण है जो निम्न स्तर के प्रोग्रामिंग सार में जाने के बिना जटिल संख्यात्मक अध्ययन करने की अनुमति देता है। और इस भाषा का अध्ययन जारी रखने के लिए यह एक उत्कृष्ट अवसर है।

सभी को शुभकामनाएँ!