🤾 🤶🏿 🎲 संबंधपरक प्रोग्रामिंग: दर्द, रुचि, और दर्द फिर से 🍈 ⛹🏽 👨🏼‍🚒

पिछली पोस्ट में हमने विस्तार से बताया कि हम "औद्योगिक प्रोग्रामिंग" के क्षेत्र में छात्रों को क्या सिखाते हैं। उन लोगों के लिए जिनकी रुचि का क्षेत्र अधिक सैद्धांतिक क्षेत्र में है, उदाहरण के लिए, प्रोग्रामिंग पर सैद्धांतिक अनुसंधान में उपयोग किए जाने वाले नए प्रोग्रामिंग प्रतिमान या सार गणित से आकर्षित, एक और विशेषज्ञता है - "प्रोग्रामिंग लैंग्वेजेस"।

आज मैं रिलेशनल प्रोग्रामिंग के क्षेत्र में अपने शोध के बारे में बात करूंगा, जो मैं विश्वविद्यालय में करता हूं और भाषा उपकरण JetBrains रिसर्च की प्रयोगशाला में एक छात्र-शोधकर्ता के रूप में।

रिलेशनल प्रोग्रामिंग क्या है? आमतौर पर हम तर्कों के साथ एक फ़ंक्शन चलाते हैं और परिणाम प्राप्त करते हैं। लेकिन संबंधपरक मामले में, आप इसके विपरीत कर सकते हैं: परिणाम और एक तर्क को ठीक करें, और दूसरा तर्क प्राप्त करें। मुख्य बात यह है कि कोड को सही ढंग से लिखें और धैर्य रखें और एक अच्छा क्लस्टर रखें।

अपने बारे में

मेरा नाम दिमित्री रोजप्लोखास है, मैं सेंट पीटर्सबर्ग एचएसई का प्रथम वर्ष का छात्र हूं, और पिछले साल मैंने "प्रोग्रामिंग लैंग्वेजेस" के क्षेत्र में अकादमिक विश्वविद्यालय के स्नातक कार्यक्रम से स्नातक किया है। स्नातक अध्ययन के तीसरे वर्ष से, मैं JetBrains अनुसंधान भाषा उपकरण प्रयोगशाला में एक शोध छात्र भी हूं।

संबंधपरक प्रोग्रामिंग

सामान्य तथ्य

रिलेशनल प्रोग्रामिंग तब होता है, जब फ़ंक्शन के बजाय, आप तर्कों और परिणाम के बीच संबंध का वर्णन करते हैं। यदि इसके लिए भाषा को तेज किया जाता है, तो आप निश्चित बोनस प्राप्त कर सकते हैं, उदाहरण के लिए, फ़ंक्शन को विपरीत दिशा में चलाने की क्षमता (परिणामस्वरूप परिणामस्वरूप तर्कों के संभावित मूल्यों को पुनर्स्थापित करें)।

सामान्य तौर पर, यह किसी भी तार्किक भाषा में किया जा सकता है, लेकिन रिलेशनल प्रोग्रामिंग में रुचि लगभग दस साल पहले एक न्यूनतर शुद्ध तार्किक भाषा मिनीक्रेन के आगमन के साथ पैदा हुई, जिसने इस तरह के संबंधों का आसानी से वर्णन और उपयोग करना संभव बना दिया।

यहां कुछ सबसे उन्नत उपयोग के मामले दिए गए हैं: आप एक प्रूफ चेकर लिख सकते हैं और इसका उपयोग साक्ष्य खोजने के लिए कर सकते हैं ( लगभग एट अल।, 2008 ) या कुछ भाषा के लिए दुभाषिया बनाएं और इसका उपयोग टेस्ट सूट प्रोग्राम ( बर्थ एट अल।, 2017 ) उत्पन्न करने के लिए करें।

सिंटेक्स और खिलौना उदाहरण

मिनीक्रेन एक छोटी भाषा है, संबंधों का वर्णन करने के लिए केवल बुनियादी गणितीय निर्माण का उपयोग किया जाता है। यह एक एम्बेडेड भाषा है, इसकी प्रधानता कुछ बाहरी भाषा के लिए एक पुस्तकालय है, और छोटे मिनीक्रेन कार्यक्रमों को किसी अन्य भाषा में एक कार्यक्रम के अंदर उपयोग किया जा सकता है।

मिनीक्रेन, एक पूरे झुंड के लिए उपयुक्त विदेशी भाषाएं। प्रारंभ में, योजना थी, हम Ocaml ( OCanren ) के लिए संस्करण के साथ काम कर रहे हैं, और पूरी सूची minikanren.org पर देखी जा सकती है। इस लेख में उदाहरण OCanren पर भी होंगे। कई कार्यान्वयन सहायक कार्यों को जोड़ते हैं, लेकिन हम केवल मूल भाषा पर ध्यान केंद्रित करेंगे।

चलो डेटा प्रकारों के साथ शुरू करते हैं। पारंपरिक रूप से, उन्हें दो प्रकारों में विभाजित किया जा सकता है:

कॉन्स्टेंट भाषा के कुछ डेटा हैं जिनमें हम एम्बेडेड हैं। स्ट्रिंग्स, नंबर, यहां तक कि सरणियाँ। लेकिन बुनियादी मिनीकरन के लिए, यह सभी एक ब्लैक बॉक्स है, स्थिरांक केवल समानता के लिए जांचे जा सकते हैं।
एक "पद" कई तत्वों का एक समूह है। हास्केल में डेटा कंस्ट्रक्टर्स के समान उपयोग किया जाता है: डेटा कंस्ट्रक्टर (स्ट्रिंग) प्लस शून्य या अधिक पैरामीटर। OCren, OCaml से नियमित डेटा कंस्ट्रक्टर्स का उपयोग करता है।

उदाहरण के लिए, यदि हम मिनीक्रेन में स्वयं सरणियों के साथ काम करना चाहते हैं, तो इसे कार्यात्मक भाषाओं के समान शब्दों के संदर्भ में वर्णित किया जाना चाहिए - एक एकल रूप से जुड़ी सूची के रूप में। एक सूची या तो एक खाली सूची है (कुछ सरल शब्द द्वारा इंगित), या सूची के पहले तत्व ("सिर") और शेष तत्वों ("पूंछ") से एक जोड़ी है।

let emptyList = Nil let list_123 = Cons (1, Cons (2, Cons (3, Nil)))

एक मिनीक्रेन कार्यक्रम कुछ चर के बीच का संबंध है। स्टार्टअप पर, कार्यक्रम सामान्य रूप में चर के सभी संभावित मूल्यों को देता है। अक्सर कार्यान्वयन आपको आउटपुट में उत्तरों की संख्या को सीमित करने की अनुमति देते हैं, उदाहरण के लिए, केवल पहले एक को ढूंढें - खोज हमेशा सभी समाधान खोजने के बाद बंद नहीं होती है।

आप कई रिश्ते लिख सकते हैं जो एक दूसरे के माध्यम से परिभाषित किए जाते हैं और यहां तक कि पुनरावर्ती कार्यों के रूप में भी कहा जाता है। उदाहरण के लिए, हम फ़ंक्शन के बजाय नीचे

अ प े ं ड (ए, ब ी) \to $ क े स ा

$अपेंड (ए, बी) → $ के सा$ संबंध परिभाषित करें

a p p e n d o (ए, ब ी, स ी)

$appendo (ए, बी, सी)$ : सूची

स ी

$सी$ सूचियों का एक संयोजन है

ए क

$एक$ और

ब

$ब$ । पारंपरिक रूप से रिश्तों को लौटाने वाले कार्य "ओ" के साथ साधारण कार्यों से अलग करने के लिए समाप्त होते हैं।

एक संबंध कुछ तर्कों के रूप में लिखा जाता है। हमारे चार बुनियादी ऑपरेशन हैं :

दो शब्दों का एकीकरण या समानता (===), शब्द चर शामिल कर सकते हैं। उदाहरण के लिए, आप संबंध "सूची" लिख सकते हैं एक तत्व के होते हैं »:
```
 let isSingletono xl = l === Cons (x, Nil) 
```
सामान्य तर्क के अनुसार, कंजंक्शन (तार्किक "और") और अव्यवस्था (तार्किक "या") -। OCanren को &&& और ||| लेकिन मिनीक्रेन में मूल रूप से कोई तार्किक इनकार नहीं है।
नए चर जोड़ना। तर्क में, यह अस्तित्व की एक मात्रा है। उदाहरण के लिए, गैर-रिक्तता के लिए सूची की जांच करने के लिए, आपको यह जांचने की आवश्यकता है कि सूची में एक सिर और एक पूंछ है। वे रिश्ते के तर्क नहीं हैं, इसलिए आपको नए चर बनाने की आवश्यकता है:
```
 let nonEmptyo l = fresh (ht) (l === Cons (h, t)) 
```

एक रिश्ता खुद को पुनरावृत्ति कर सकता है। उदाहरण के लिए, आपको संबंध "तत्व" को परिभाषित करने की आवश्यकता है

x

$x$ सूची में निहित है। " हम तुच्छ मामलों का विश्लेषण करके इस समस्या को हल करेंगे, जैसा कि कार्यात्मक भाषाओं में है:

या सूची का प्रमुख है $x$
या $x$ पूँछ में झूठ

 let membero lx = fresh (ht) ( (l === Cons (h, t)) &&& (x === h ||| membero tx) )

भाषा का मूल संस्करण इन चार परिचालनों पर बनाया गया है। ऐसे एक्सटेंशन भी हैं जो आपको अन्य ऑपरेशन का उपयोग करने की अनुमति देते हैं। उनमें से सबसे उपयोगी दो शर्तों (= / =) की असमानता को स्थापित करने के लिए असमानता बाधा है।

अतिसूक्ष्मवाद के बावजूद, मिनीक्रेन काफी अभिव्यंजक भाषा है। उदाहरण के लिए, दो सूचियों के संबंधपरक संघटन को देखें। दो तर्कों का कार्य ट्रिपल रिलेशन में बदल जाता है "

अ ब

$अब$ सूचियों का एक संयोजन है

ए क

$एक$ और

ब

$ब$ "।

 let appendo ab ab = (a === Nil &&& ab === b) ||| (fresh (ht tb) (*  :  fresh   &&& *) (a = Cons (h, t)) (appendo tb tb) (ab === Cons (h, tb)))

समाधान संरचनात्मक रूप से अलग नहीं है कि हम इसे कार्यात्मक भाषा में कैसे लिखेंगे। हम एक खंड द्वारा एकजुट दो मामलों का विश्लेषण करते हैं:

यदि पहली सूची खाली है, तो दूसरी सूची और नतीजे के परिणाम बराबर हैं।
यदि पहली सूची खाली नहीं है, तो हम इसे सिर और पूंछ में पार्स करते हैं और संबंध के पुनरावर्ती कॉल का उपयोग करके परिणाम का निर्माण करते हैं।

हम इस संबंध के लिए अनुरोध कर सकते हैं, पहला और दूसरा तर्क तय कर सकते हैं - हमें सूचियों का निष्कर्ष मिलता है:

 run 1 (λ q -> appendo (Cons (1, Cons (2, Nil))) (Cons (3, Cons (4, Nil))) q)

⇒

 q = Cons (1, Cons (2, Cons (3, Cons (4, Nil))))

हम अंतिम तर्क को ठीक कर सकते हैं - हमें इस सूची के सभी विभाजन दो में मिलते हैं।

 run 4 (λ qr -> appendo qr (Cons (1, Cons (2, Cons (3, Nil)))))

⇒

 q = Nil, r = Cons (1, Cons (2, Cons (3, Nil))) | q = Cons (1, Nil), r = Cons (2, Cons (3, Nil)) | q = Cons (1, Cons (2, Nil)), r = Cons (3, Nil) | q = Cons (1, Cons (2, Cons (3, Nil))), r = Nil

आप कुछ और भी कर सकते हैं। थोड़ा और गैर-मानक उदाहरण, जिसमें हम केवल तर्कों का हिस्सा तय करते हैं:

 run 1 (λ qr -> appendo (Cons (1, Cons (q, Nil))) r (Cons (1, Cons (2, Cons (3, Cons (4, Nil))))))

⇒

 q = 2, r = Cons (3, Cons (4, Nil))

यह कैसे काम करता है

सिद्धांत के दृष्टिकोण से, यहां कुछ भी प्रभावशाली नहीं है: आप हमेशा सभी तर्कों के लिए सभी संभावित विकल्पों की खोज शुरू कर सकते हैं, प्रत्येक सेट की जांच कर सकते हैं कि क्या वे किसी दिए गए फ़ंक्शन / संबंध के संबंध में व्यवहार करते हैं जैसा कि हम चाहते हैं (देखें "ब्रिटिश संग्रहालय एल्गोरिथम ) । रुचि का तथ्य यह है कि यहां खोज (दूसरे शब्दों में, समाधान की खोज) वर्णित रिश्ते की संरचना का उपयोग करती है, जिसके कारण यह व्यवहार में अपेक्षाकृत प्रभावी हो सकता है।

खोज वर्तमान स्थिति में विभिन्न चर के बारे में जानकारी जमा करने के संबंध में है। हम या तो प्रत्येक चर के बारे में कुछ भी नहीं जानते हैं, या हम जानते हैं कि इसे शब्दों, मूल्यों और अन्य चर में कैसे व्यक्त किया जाता है। उदाहरण के लिए:

b = Cons (x, y)
c = Cons (10, z)
x = ?
y = ?
z = ?

एकीकरण से गुजरते हुए, हम इस जानकारी को ध्यान में रखते हुए दो शब्दों को देखते हैं और या तो स्थिति को अपडेट करते हैं या खोज को समाप्त करते हैं यदि दो शब्दों को एकीकृत नहीं किया जा सकता है। उदाहरण के लिए, एकीकरण b = c को पूरा करने पर, हमें नई जानकारी मिलती है: x = 10, y = z। लेकिन एकीकरण बी = निल एक विरोधाभास का कारण होगा।

हम क्रमिक रूप से खोज करते हैं (ताकि जानकारी संचित हो जाए), और एक अव्यवस्था में हम खोज को दो समानांतर शाखाओं में विभाजित करते हैं और आगे बढ़ते हैं, बारी-बारी से उनमें कदम रखते हैं - यह तथाकथित इंटरलेविंग खोज है। इस विकल्प के लिए धन्यवाद, खोज पूर्ण है - प्रत्येक उपयुक्त समाधान एक परिमित समय के बाद मिलेगा। उदाहरण के लिए, प्रोलॉग भाषा में ऐसा नहीं है। यह एक गहरे क्रॉल (जो एक अनंत शाखा पर लटका सकता है) की तरह कुछ करता है, और इंटरलेइंग खोज अनिवार्य रूप से एक ट्रिकी चौड़ा क्रॉल संशोधन है।

आइए अब देखें कि पिछले अनुभाग से पहली क्वेरी कैसे काम करती है। चूंकि appendo में पुनरावर्ती कॉल हैं, इसलिए हम उन्हें अलग करने के लिए चर में अनुक्रमित जोड़ देंगे। नीचे दिया गया चित्र एन्यूमरेशन ट्री दिखाता है। तीर जानकारी के प्रसार की दिशा को इंगित करता है (पुनरावृत्ति से वापसी के अपवाद के साथ)। विघटन के बीच, जानकारी वितरित नहीं की जाती है, और बीच में बांए से दाएं वितरित की जाती है।

हम appendo के लिए एक बाहरी कॉल के साथ शुरू करते हैं। विवाद के कारण वामपंथ की शाखा मर गई: सूची $एक$ खाली नहीं।
सही शाखा में सहायक चर पेश किए जाते हैं, जो तब सूची को "पार्स" करने के लिए उपयोग किए जाते हैं $a_1$ सिर और पूंछ पर।
इसके बाद, appendo पुनरावर्ती कॉल एक = [2], बी = [3, 4], एबी =? के लिए होता है? जिसमें समान संचालन होते हैं।
लेकिन अपेंडो के लिए तीसरी कॉल में हमारे पास पहले से ही एक = [], बी = [३,४], एब =? और फिर बाईं ओर की छूट सिर्फ काम करती है, जिसके बाद हमें सूचना मिलती है अब = बी। लेकिन सही शाखा में एक विरोधाभास है।
अब हम सभी उपलब्ध सूचनाओं को लिख सकते हैं और चर के मानों को प्रतिस्थापित करके उत्तर को पुनर्स्थापित कर सकते हैं:

a_1 = [1, 2] b_1 = [3, 4] ab_1 = Cons h_1 tb_1 h_1 = 1 a_2 = t_1 = [2] b_2 = b_1 = [3, 4] ab_2 = tb_1 = Cons h_2 tb_2 h_2 = 2 a_3 = t_2 = Nil b_3 = b_2 = b_1 = [3, 4] ab_3 = tb_2 = b_3 = [3, 4]
यह इस प्रकार है $ab_1$ = विपक्ष (1, विपक्ष (2, [3, 4])) = [1, 2, 3, 4], आवश्यकतानुसार।

मैंने स्नातक में क्या किया

सब कुछ धीमा हो जाता है

हमेशा की तरह: वे आपसे वादा करते हैं कि सब कुछ सुपर घोषणापत्र होगा, लेकिन वास्तव में आपको भाषा के अनुकूल होने की जरूरत है और सब कुछ एक विशेष तरीके से (ध्यान में रखते हुए कि सब कुछ कैसे निष्पादित किया जाएगा) कम से कम कुछ काम करने के लिए, सबसे सरल उदाहरणों को छोड़कर। यह निराशाजनक है।

एक नौसिखिए मिनीक्रेन प्रोग्रामर की पहली समस्याओं में से एक यह है कि यह बहुत हद तक उस क्रम पर निर्भर करता है जिसमें आप प्रोग्राम में शर्तों (संयोजन) का वर्णन करते हैं। एक आदेश के साथ, सब कुछ ठीक है, लेकिन दो संयुग्मों की अदला-बदली की गई और सब कुछ बहुत धीरे-धीरे काम करना शुरू कर दिया या बिल्कुल भी खत्म नहीं हुआ। यह अप्रत्याशित है।

यहां तक कि ऐपेंडो के साथ उदाहरण में, विपरीत दिशा में लॉन्च करना (सूची को दो में विभाजित करना) तब तक समाप्त नहीं होता है जब तक आप स्पष्ट रूप से निर्दिष्ट नहीं करते हैं कि आप कितने उत्तर चाहते हैं (फिर आवश्यक संख्या पाए जाने पर खोज समाप्त हो जाएगी)।

मान लें कि हम मूल चर को निम्नानुसार ठीक करते हैं: a = ?, B = ?, Ab = [1, 2, 3] (नीचे दिया गया आंकड़ा देखें) दूसरी शाखा में, इस जानकारी का उपयोग किसी भी तरह से पुनरावर्ती कॉल के दौरान नहीं किया जाएगा (चर अब और प्रतिबंध)

h_{1}

$h_1$ और

t b_{1}

$tb_1$ इस कॉल के बाद ही दिखाई देंगे)। इसलिए, पहले पुनरावर्ती कॉल पर, इसके सभी तर्क मुफ्त चर होंगे। यह कॉल दो सूचियों और उनके संयोजन (और यह पीढ़ी कभी खत्म नहीं होगी) से सभी प्रकार के त्रिभुज उत्पन्न करेगा, और फिर उनमें से उन को चुना जाएगा जिनके लिए तीसरा तत्व ठीक उसी तरह से निकला जिस तरह से हमें ज़रूरत है।

सब कुछ उतना बुरा नहीं है जितना पहली नज़र में लग सकता है, क्योंकि हम बड़े समूहों में इन तीनों के माध्यम से हल करेंगे। एक ही लंबाई के साथ सूचियाँ लेकिन विभिन्न तत्व फ़ंक्शन के दृष्टिकोण से भिन्न नहीं होते हैं, इसलिए वे एक समाधान में गिर जाएंगे - तत्वों के स्थान पर मुफ्त चर होंगे। फिर भी, हम अभी भी सभी संभावित सूची लंबाई के माध्यम से छंटनी करेंगे, हालांकि हमें केवल एक की आवश्यकता है, और हम जानते हैं कि कौन सा है। यह खोज में जानकारी का एक बहुत ही तर्कहीन उपयोग (गैर-उपयोग) है।

इस विशिष्ट उदाहरण को ठीक करना आसान है: आपको बस पुनरावर्ती कॉल को अंत तक स्थानांतरित करने की आवश्यकता है और सब कुछ उसी तरह काम करेगा जैसे इसे करना चाहिए। पुनरावर्ती कॉल से पहले, वेरिएबल एब के साथ एकीकरण होगा और पुनरावर्ती कॉल दी गई सूची (एक सामान्य पुनरावर्ती कार्य के रूप में) की पूंछ से किया जाएगा। अंत में एक पुनरावर्ती कॉल के साथ यह परिभाषा सभी दिशाओं में अच्छी तरह से काम करेगी: पुनरावर्ती कॉल के लिए, हम तर्कों के बारे में सभी संभावित जानकारी संचित करने का प्रबंधन करते हैं।

हालांकि, किसी भी अधिक जटिल उदाहरण में, जब कई सार्थक कॉल होते हैं, तो एक विशिष्ट क्रम जिसके लिए सब कुछ ठीक होगा मौजूद नहीं है। सबसे सरल उदाहरण: समवर्ती का उपयोग करके एक सूची का विस्तार करना। हम पहले तर्क को ठीक करते हैं - हमें इस विशेष आदेश की आवश्यकता है, हम दूसरे को ठीक करते हैं - हमें कॉल स्वैप करने की आवश्यकता है। अन्यथा, यह लंबे समय तक खोजा जाता है और खोज समाप्त नहीं होती है।

 reverso x xr = (x === Nil &&& xr == Nil) ||| (fresh (ht tr) (x === Cons (h, t)) (reverso t tr) (appendo tr (Cons (h, Nil)) xr))

ऐसा इसलिए है क्योंकि खोज प्रक्रियाओं को क्रमिक रूप से क्रमिक रूप से नियंत्रित किया जाता है, और कोई भी स्वीकार्य दक्षता को खोए बिना इसे अलग तरीके से करने के लिए नहीं आ सकता है, हालांकि उन्होंने कोशिश की। बेशक, किसी दिन सभी समाधान मिल जाएंगे, लेकिन गलत क्रम के साथ, उन्हें इतने लंबे समय तक अप्रकाशित रूप से खोजा जाएगा कि इसमें कोई व्यावहारिक अर्थ नहीं है।

इस समस्या से बचने के लिए कार्यक्रम लिखने की तकनीकें हैं। लेकिन उनमें से कई को उपयोग करने के लिए विशेष कौशल और कल्पना की आवश्यकता होती है, और इसका परिणाम बहुत बड़े कार्यक्रम हैं। एक उदाहरण शब्द आकार सीमा तकनीक है और बाइनरी डिवीजन की परिभाषा इसकी सहायता से गुणा के माध्यम से शेष है। इसके बजाय मूर्खतापूर्ण रूप से गणितीय परिभाषा लिखना

 divo nmqr = (fresh (mq) (multo mq mq) (pluso mq rn) (lto rm))

मुझे 20 लाइनों + एक बड़े सहायक फ़ंक्शन की पुनरावर्ती परिभाषा लिखना है जो पढ़ने के लिए अवास्तविक है (मुझे अभी भी समझ नहीं है कि वहां क्या किया जा रहा है)। यह शुद्ध बाइनरी अरिथमेटिक सेक्शन में विल बर्ड के शोध प्रबंध में पाया जा सकता है।

पूर्वगामी को देखते हुए, मैं कुछ प्रकार के खोज संशोधन के साथ आना चाहूंगा ताकि सरल और स्वाभाविक रूप से लिखित कार्यक्रम भी काम करें।

अनुकूलन

हमने देखा कि जब सब कुछ खराब है, तो खोज तब तक समाप्त नहीं होगी जब तक आप स्पष्ट रूप से उत्तर की संख्या का संकेत नहीं देते और इसे तोड़ नहीं देते। इसलिए, उन्होंने खोज की अपूर्णता के साथ सटीक रूप से लड़ने का फैसला किया - यह "लंबे समय तक काम करता है" की तुलना में समवर्ती करना बहुत आसान है। सामान्य तौर पर, मैं बस खोज को गति देना चाहता हूं, लेकिन इसे औपचारिक रूप देना अधिक कठिन है, इसलिए हमने कम महत्वाकांक्षी कार्य के साथ शुरुआत की।

ज्यादातर मामलों में, जब खोज में परिवर्तन होता है, तो ऐसी स्थिति उत्पन्न होती है जिसे ट्रैक करना आसान होता है। यदि एक फ़ंक्शन को पुनरावर्ती कहा जाता है, और एक पुनरावर्ती कॉल में, तर्क समान या कम विशिष्ट होते हैं, तो पुनरावर्ती कॉल में इस तरह के एक और उपशीर्षक फिर से उत्पन्न होते हैं और अनंत पुनरावृत्ति होती है। औपचारिक रूप से, यह इस तरह से लगता है: एक प्रतिस्थापन है, जो नए तर्कों पर लागू होता है, हमें पुराने मिलते हैं। उदाहरण के लिए, नीचे दिए गए चित्र में, पुनरावर्ती कॉल मूल का एक सामान्यीकरण है: आप स्थानापन्न कर सकते हैं

c_{2}

$c_2$ = [एक्स, 3],

d_{2}

$d_2$ = x और मूल कॉल प्राप्त करें।

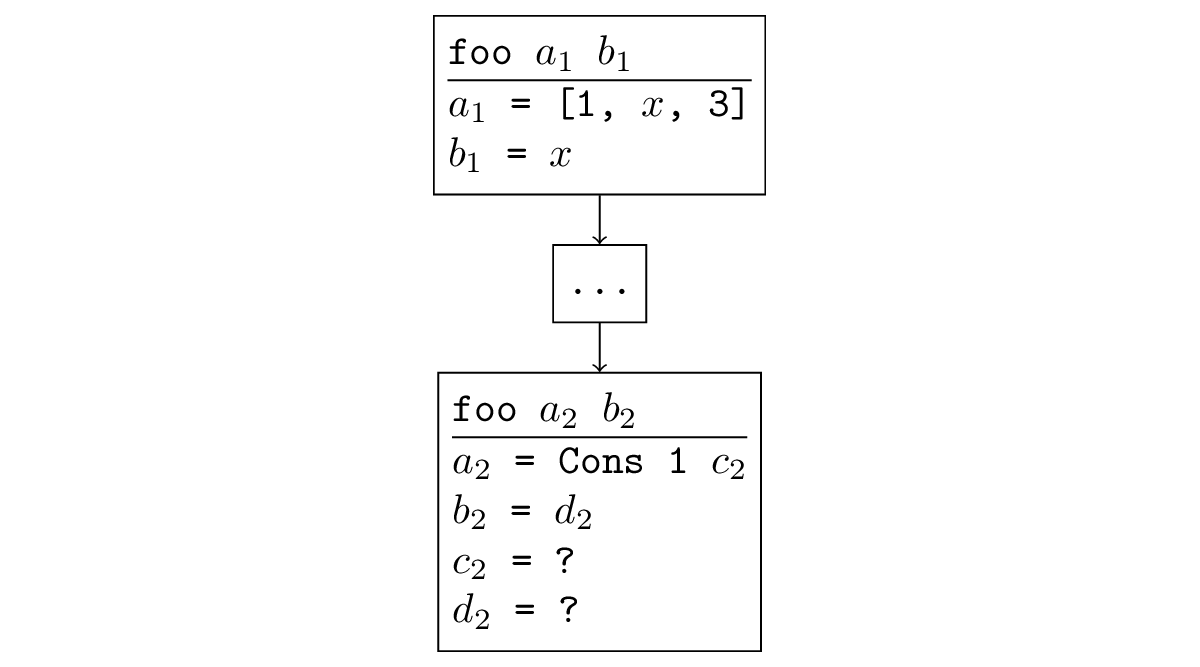
यह पता लगाया जा सकता है कि यह स्थिति उस विचलन के उदाहरणों में भी होती है जो हम पहले ही मिल चुके हैं। जैसा कि मैंने पहले लिखा था, जब आप विपरीत दिशा में एपेन्डो चलाते हैं, तो सभी वेरिएबल्स के बजाय फ्री वैरिएबल के साथ एक रिर्ससिव कॉल किया जाएगा, जो निश्चित रूप से मूल कॉल की तुलना में कम विशिष्ट है, जिसमें तीसरा तर्क तय किया गया था।

यदि हम x = के साथ रिवर्सलो चलाते हैं? और xr = [1, 2, 3], यह देखा जा सकता है कि पहली पुनरावर्ती कॉल फिर से दो मुक्त चर के साथ होगी, इसलिए नए तर्क फिर से स्पष्ट रूप से पिछले वाले को स्थानांतरित किए जा सकते हैं।

 reverso x x_r  (* x = ?, x_r = [1, 2, 3] *) fresh (ht t_r) (x === Cons (h, t)) (* x_r = [1, 2, 3] = Cons 1 (Cons 2 (Cons 3 Nil))) x = Cons (h, t) *) (reverso t t_r) (* :   t=x, t_r=[1,2,3],    *)

इस मानदंड का उपयोग करके, हम कार्यक्रम निष्पादन की प्रक्रिया में विचलन का पता लगा सकते हैं, समझ सकते हैं कि इस आदेश के साथ सब कुछ खराब है, और गतिशील रूप से इसे दूसरे में बदल दें। इसके लिए धन्यवाद, आदर्श रूप से, प्रत्येक कॉल के लिए बस सही क्रम का चयन किया जाएगा।
आप इसे भोलेपन से कर सकते हैं: यदि संयोजन में विचलन पाया जाता है, तो हम उन सभी उत्तरों में हथौड़ा करते हैं जो उन्होंने पहले ही पाए थे और बाद में इसके निष्पादन को स्थगित कर दिया, अगले संयोजन को "आगे" छोड़ दिया। फिर, शायद, जब हम इसे निष्पादित करना जारी रखेंगे, तो अधिक जानकारी पहले से ही ज्ञात हो जाएगी और विचलन उत्पन्न नहीं होगा। हमारे उदाहरणों में, यह वांछित स्वैप संयोजनों को जन्म देगा।

कम भोले तरीके हैं जो अनुमति देते हैं, उदाहरण के लिए, पहले से किए गए काम को नहीं खोना, प्रदर्शन को स्थगित करना। पहले से ही आदेश को बदलने के सबसे बेवकूफ संस्करण के साथ, विचलन सभी सरल उदाहरणों में गायब हो गया है जो संयोजन के गैर-कम्यूटेटिविटी से पीड़ित है, जिसे हम जानते हैं, जिसमें शामिल हैं:

संख्याओं की सूची छाँटना (यह सूची के सभी क्रमपरिवर्तन की पीढ़ी भी है),
पीनो अंकगणित और द्विआधारी अंकगणित,
किसी दिए गए आकार के द्विआधारी पेड़ों की पीढ़ी।

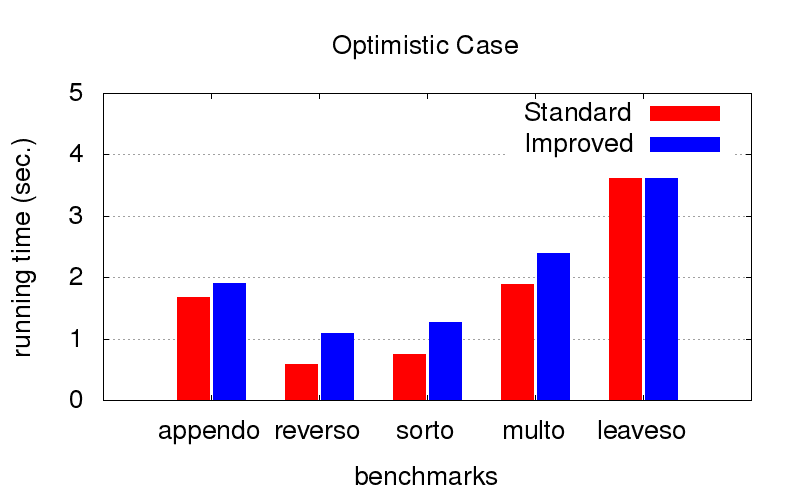
यह हमारे लिए एक अप्रत्याशित आश्चर्य था। विचलन के अलावा, अनुकूलन कार्यक्रम के मंदी के खिलाफ भी लड़ता है। नीचे दिए गए आरेख कार्यक्रमों के निष्पादन के समय को दो अलग-अलग आदेशों के साथ संयोजन में दिखाते हैं (अपेक्षाकृत बोलना, सबसे अच्छा में से एक और कई बुरे में से एक)। यह उबंटू 16.04 ऑपरेटिंग सिस्टम के साथ Intel Core i7 CPU M 620, 2.67GHz x 4, 8GB RAM के कॉन्फ़िगरेशन वाले कंप्यूटर पर लॉन्च किया गया था।

जब आदेश पहले से ही इष्टतम है (हम इसे हाथ से चुनते हैं), तो अनुकूलन निष्पादन को थोड़ा धीमा कर देता है, लेकिन महत्वपूर्ण नहीं है

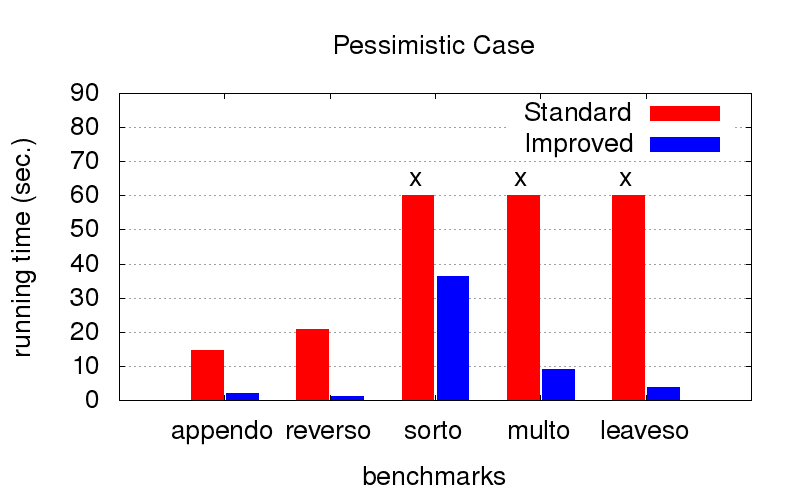
लेकिन जब आदेश इष्टतम नहीं होता है (उदाहरण के लिए, केवल विपरीत दिशा में लॉन्च करने के लिए उपयुक्त), अनुकूलन के साथ यह बहुत तेजी से निकलता है। क्रॉस का मतलब है कि हम सिर्फ अंत का इंतजार नहीं कर सकते थे, यह बहुत लंबे समय तक काम करता है

कैसे कुछ नहीं तोड़ने के लिए

यह सब विशुद्ध रूप से अंतर्ज्ञान पर आधारित था और हम इसे सख्ती से सिद्ध करना चाहते थे। आखिरकार थ्योरी।

कुछ साबित करने के लिए, हमें भाषा के औपचारिक शब्दार्थ की आवश्यकता होती है। हमने मिनीक्रेन के लिए परिचालन शब्दार्थ का वर्णन किया। यह एक वास्तविक भाषा कार्यान्वयन का एक सरलीकृत और गणितीय संस्करण है। यह एक बहुत ही सीमित (इसलिए उपयोग में आसान) संस्करण का उपयोग करता है, जिसमें आप केवल कार्यक्रमों के अंतिम निष्पादन (खोज अंतिम होना चाहिए) को निर्दिष्ट कर सकते हैं। लेकिन हमारे उद्देश्यों के लिए यह वही है जिसकी आवश्यकता है।

कसौटी पर खरा उतरने के लिए, लेम्मा को पहले तैयार किया जाता है: अधिक सामान्य स्थिति से प्रोग्राम निष्पादन लंबे समय तक काम करेगा। औपचारिक रूप से: शब्दार्थ में आउटपुट ट्री की एक बड़ी ऊंचाई है। यह प्रेरण द्वारा सिद्ध किया गया है, लेकिन बयान को बहुत सावधानी से सामान्यीकृत किया जाना चाहिए, अन्यथा प्रेरक परिकल्पना पर्याप्त मजबूत नहीं होगी। इस लेम्मा से यह निकलता है कि यदि प्रोग्राम के निष्पादन के दौरान कोई मानदंड काम करता है, तो आउटपुट ट्री का अपना अधिक से अधिक या बराबर ऊंचाई का उप योग है। यह एक विरोधाभास देता है, क्योंकि प्रत्यक्ष रूप से दिए गए शब्दार्थ के लिए सभी पेड़ परिमित हैं। इसका मतलब यह है कि हमारे शब्दार्थ में इस कार्यक्रम का निष्पादन अक्षम्य है, जिसका अर्थ है कि इसमें खोज समाप्त नहीं होती है।

प्रस्तावित विधि रूढ़िवादी है: हम केवल तभी कुछ बदलते हैं जब हम आश्वस्त होते हैं कि सब कुछ पहले से ही खराब है और बदतर करने के लिए असंभव है, इसलिए हम कार्यक्रम पूरा होने के मामले में कुछ भी नहीं तोड़ते हैं।

मुख्य प्रमाण में बहुत सारे विवरण शामिल हैं, इसलिए हमें Coq लिखकर औपचारिक रूप से इसे सत्यापित करने की इच्छा थी। हालाँकि, यह तकनीकी रूप से काफी कठिन था, इसलिए हमने अपने आर्दोर को ठंडा कर दिया और गंभीरता से केवल मैजिस्ट्रेटरी में स्वचालित सत्यापन में लगे रहे।

प्रकाशन

काम के बीच में, हमने इस अध्ययन को छात्र अनुसंधान प्रतियोगिता में ICFP-2017 के पोस्टर सत्र में प्रस्तुत किया। वहाँ हम भाषा के रचनाकारों - विल बर्ड और डैनियल फ्रीडमैन से मिले - और उन्होंने कहा कि यह सार्थक है और हमें इसे और अधिक विस्तार से देखने की आवश्यकता है। वैसे, विल आम तौर पर JetBrains रिसर्च में हमारी प्रयोगशाला के साथ दोस्त हैं। मिनीक्रेन पर हमारे सभी शोध तब शुरू हुए, जब 2015 में, विल सेंट पीटर्सबर्ग में रिलेशनल प्रोग्रामिंग में एक ग्रीष्मकालीन स्कूल का आयोजन किया।

एक साल बाद, हम अपने काम को अधिक या कम पूर्ण रूप में ले आए और लेख और प्रैक्टिकल प्रोग्रामिंग 2018 के सिद्धांतों पर लेख प्रस्तुत किया।

मैं ग्रेजुएट स्कूल में क्या करूँ?

हम मिनीक्रेन और इसके सभी गुणों के कठोर प्रमाण के लिए औपचारिक शब्दार्थ में संलग्न रहना चाहते थे। साहित्य में, आमतौर पर गुणों (अक्सर स्पष्ट से दूर) को उदाहरणों का उपयोग करके केवल पोस्ट किया और प्रदर्शित किया जाता है, लेकिन कोई भी कुछ भी साबित नहीं करता है। उदाहरण के लिए, रिलेशनल प्रोग्रामिंग पर मुख्य पुस्तक प्रश्नों और उत्तरों की एक सूची है, जिनमें से प्रत्येक कोड के एक विशिष्ट टुकड़े के लिए समर्पित है। यहां तक कि इंटरलेविंग खोज की पूर्णता के बयान के लिए (और यह मानक प्रोलॉग पर मिनीक्रेन के सबसे महत्वपूर्ण लाभों में से एक है), एक सख्त शब्द खोजना असंभव है। आप उस तरह नहीं रह सकते, जैसा हमने तय किया, और, विल से आशीर्वाद प्राप्त करने के बाद, हमने काम करने की ठानी।

मैं आपको याद दिलाता हूं कि पिछले चरण में हमने जो शब्दार्थ विकसित किया था, उसकी एक महत्वपूर्ण सीमा थी: केवल परिमित खोज वाले कार्यक्रमों का वर्णन किया गया था। मिनीक्रेन में, चल रहे कार्यक्रम भी दिलचस्प हैं क्योंकि वे अनंत संख्या में उत्तर सूचीबद्ध कर सकते हैं। इसलिए, हमें और अधिक शांत शब्दों की ज़रूरत थी।

एक प्रोग्रामिंग भाषा के शब्दार्थ को परिभाषित करने के लिए कई अलग-अलग मानक तरीके हैं, हमें केवल उनमें से एक को चुनना था और इसे एक विशिष्ट मामले में अनुकूलित करना था। हमने शब्दार्थ को एक लेबल संक्रमण प्रणाली के रूप में वर्णित किया - इन राज्यों के बीच खोज प्रक्रिया और संक्रमण में संभावित राज्यों का एक सेट, जिनमें से कुछ चिह्नित हैं, जिसका अर्थ है कि खोज के वर्तमान चरण में, एक और उत्तर मिला था। एक विशेष कार्यक्रम का निष्पादन इस तरह के संक्रमण के अनुक्रम द्वारा निर्धारित किया जाता है। ये क्रम एक परिमित हो सकते हैं (एक टर्मिनल राज्य में आ रहे हैं) या अनंत, एक साथ समाप्ति और कार्यक्रमों को पूरा नहीं करने का वर्णन करते हैं। गणितीय रूप से इस तरह के ऑब्जेक्ट को पूरी तरह से निर्दिष्ट करने के लिए, किसी को एक सहवर्ती परिभाषा का उपयोग करने की आवश्यकता होती है।

ऊपर वर्णित शब्दार्थ परिचालन है - यह खोज के वास्तविक कार्यान्वयन को दर्शाता है। इसके अतिरिक्त, हम डिमोनेटिक शब्दार्थों का भी उपयोग करते हैं , जो कुछ गणितीय वस्तुओं को भाषा कार्यक्रमों और निर्माणों में प्राकृतिक कार्यक्रमों के साथ जोड़ते हैं (उदाहरण के लिए, एक कार्यक्रम में संबंधों को विभिन्न शर्तों पर संबंधों के रूप में माना जाता है, एक संयोजन संबंधों का एक चौराहा है, आदि)। इस तरह के शब्दार्थ को परिभाषित करने का मानक तरीका सबसे छोटे एरब्रान मॉडल के रूप में जाना जाता है, और मिनीक्रेन के लिए यह पहले से ही (हमारी प्रयोगशाला में भी) किया जा चुका है।

उसके बाद, भाषा में खोज की पूर्णता, और शुद्धता के साथ, इन दो शब्दार्थों के समतुल्य के रूप में तैयार किया जा सकता है - उनमें एक विशिष्ट कार्यक्रम के लिए उत्तरों के सेट का संयोग। हम इसे साबित करने में कामयाब रहे। यह दिलचस्प (और थोड़ा दुखद) है कि हमने अलग-अलग मापदंडों के साथ कई नेस्टेड प्रेरणों का उपयोग किए बिना सह-प्रेरण के बिना किया।
एक कोरोलरी के रूप में, हम कुछ उपयोगी भाषा परिवर्तनों (प्राप्त समाधानों के सेट के संदर्भ में) की शुद्धता भी प्राप्त करते हैं: यदि परिवर्तन स्पष्ट रूप से संबंधित गणितीय वस्तु को नहीं बदलता है, उदाहरण के लिए, संयुग्मन को पुन: व्यवस्थित करना या वितरणात्मक संयुग्मन या विक्षेप का उपयोग करना, तो खोज परिणाम नहीं बदलते हैं।

अब हम भाषा के अन्य उपयोगी गुणों को साबित करने के लिए शब्दार्थ का उपयोग करना चाहते हैं, उदाहरण के लिए, पूर्णता / विचलन के लिए मानदंड या अतिरिक्त भाषा निर्माण की शुद्धता।

हमने Coq का उपयोग करके हमारी औपचारिकता के एक कठोर विवरण पर भी अधिक विस्तृत नज़र डाली। कई अलग-अलग कठिनाइयों को दूर करने और बहुत सारे प्रयासों का निवेश करने के बाद, हम इस समय भाषा के परिचालन शब्दार्थों को निर्धारित करने और कुछ सबूतों का संचालन करने में सक्षम थे, जो कागज के एक टुकड़े पर था। Qed। " हम खुद पर विश्वास नहीं खोते हैं।

संबंधपरक प्रोग्रामिंग: दर्द, रुचि, और दर्द फिर से