अपरिमेय संख्या में भग्न

यह लेख मेरे पहले लेख , फ्रैक्टल्स इन प्राइम नंबर की एक निरंतरता है।

अगला लेख: तर्कहीन संख्याओं में भिन्नता। भाग २



पिछले लेख में, हमने सीखा कि पारस्परिक रूप से अभाज्य संख्याओं का उपयोग करके स्व-समान पैटर्न कैसे बनाएं। इस लेख में मैं संख्या की भग्न प्रकृति दिखाऊंगा $$$\ sqrt {2}$ ।
बिना किसी पूर्वाभास के। बिल्ली के नीचे।

हम शब्दावली और अंकन को परिभाषित करेंगे। गणित में, नीचे वर्णित प्रणालियों को बिलियर्ड्स कहा जाता है। आगे हम इस शब्द का उपयोग करेंगे। आयताकार बिलियर्ड्स के आयामों को निरूपित किया जाएगा $$$एम$ (चौड़ाई) और $$$एन$ (ऊंचाई)।

बाइनरी बिलियर्ड्स

पिछले लेख में, हमने पक्षों के साथ एक आयताकार बिलियर्ड लिया $$$एम$ और $$$एन$ इसमें एक गेंद को लॉन्च किया और सेल के माध्यम से धराशायी रेखा के साथ प्रक्षेपवक्र को चिह्नित किया:



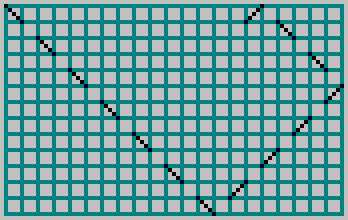
परस्पर सरल के लिए $$$एम$ और $$$एन$ हमें पैटर्न मिलता है:



बाइनरी संस्करण में, हम प्रक्षेपवक्र को धराशायी रेखा के साथ नहीं चिह्नित करते हैं, लेकिन वैकल्पिक रूप से कोशिकाओं को काले और सफेद रंग के साथ चित्रित करते हैं (हम एक बाइनरी सरणी बनाते हैं, काले के लिए 0 और इसी सेल में सफेद के लिए 1):



सीमा प्रतिबिंब नियम:



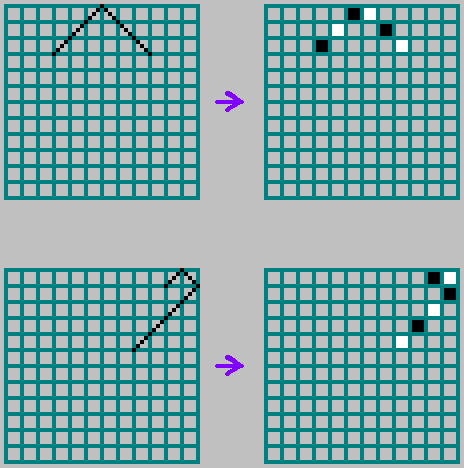
परस्पर सरल के लिए $$$एम$ और $$$एन$ प्रक्षेपवक्र प्रत्येक कोशिका से होकर गुजरता है:




यदि पार्टियों में एक सामान्य भाजक होता है, तो प्रत्येक कोने से गुजरने से पहले गेंद कोने में प्रवेश करती है:



पक्षों के साथ एक आयत में इस मामले को बिलियर्ड्स के रूप में मानना ​​सुविधाजनक है $$$\ frac {M} {GCD}$ और $$$\ frac {N} {GCD}$ (जीसीडी सबसे बड़ा सामान्य कारक है):



आगे बढ़ने से पहले, अपने लेख में उपयोगकर्ता Captain1312 द्वारा प्रस्तावित तालिका भरें (हम बिलियर्ड्स के किनारों को बीसीडी में विभाजित करेंगे)।

$$$(1, 0)$ एक सा

प्रत्येक पूल टेबल के लिए $$$एम$ और $$$एन$ निर्देशांक के साथ थोड़ा सा लें $$$(1, 0)$ ।



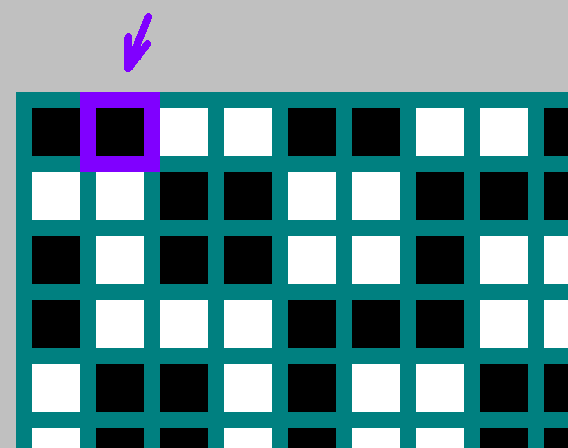
अगर $$$एम$ एक विभक्त है $$$एन$ - फिर निर्देशांक के साथ थोड़ा $$$(1, 0)$ लापता ( $$$\ frac {M} {GCD} = 1$ )। इस मामले में, हम निर्देशांक के साथ उल्टे बिट को लेते हैं $$$(0, 1)$ ।

तालिका में भरें। मूल ऊपरी बाएँ कोने है। पर $$$x$ - बिलियर्ड्स की चौड़ाई $$$एम$ पर $$$य$ - ऊंचाई $$$एन$ । प्रत्येक बिलियर्ड के लिए हम थोड़ा चिह्नित करते हैं $$$(1, 0)$ , या उलटा सा $$$(0, 1)$ (हम नीचे इस विषय पर लौटेंगे)।

बाइनरी अनुक्रम

जब हम बिलियर्ड्स की चौड़ाई को थोड़ा सा बढ़ाते हैं, तो हम क्यों उलटते हैं $$$M = 1$ ? परस्पर सरल के लिए $$$एम$ और $$$एन$ गेंद का प्रक्षेपवक्र प्रत्येक कोशिका से होकर गुजरता है। बिलियर्ड्स की ऊपरी और बाईं दीवारों के बीच, गेंद हर बार कोशिकाओं की संख्या को पार करती है।





बाएं कॉलम में बिट्स शीर्ष पंक्ति से उल्टे बिट्स हैं। हम शून्य बिट नहीं लेते हैं - प्रक्षेपवक्र इसके साथ शुरू होता है:



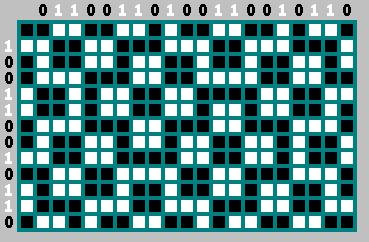
इसके अलावा, हम सुरक्षित रूप से हर दूसरे बिट को इस क्रम से बाहर निकाल सकते हैं (बिट) $$$2_ {n-1}$ - उल्टा सा $$$2_ {n}$ ):



अनुक्रम मिला $$$10 100 110 110$ बिलियर्ड्स के लिए $$$(21,13)$ । यह क्रम सभी के लिए अद्वितीय है। $$$एम$ और $$$एन$ ।

जो भी ऊंचाई हो $$$एन$ हमने हमेशा नहीं लिया - गेंद हमेशा प्रक्षेपवक्र के साथ जाती है $$$2N$ ऊपर की दीवार से दो प्रतिबिंबों के बीच। शीर्ष दीवार से, आंदोलन हमेशा "0" बिट (ब्लैक सेल) से शुरू होता है और "1" बिट (सफेद सेल) के साथ समाप्त होता है:



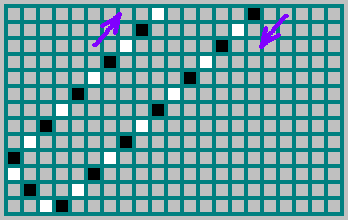
वास्तव में, अनुक्रम (जो हमने ऊपर प्रकाश डाला है - $$$10 100 110 110$ ) दिखाता है कि गेंद किस तरफ से उड़ती है: 1 - अगर गेंद अंदर उड़ती है, तो दाएं दीवार से परावर्तित होती है और 0 - यदि गेंद अंदर उड़ती है, तो बाईं दीवार से परावर्तित होती है। चित्र में, गेंद के प्रक्षेपवक्र को काले रंग से चिह्नित किया जाता है यदि गेंद दाईं ओर और सफेद बाईं ओर ले जाए तो:




यह क्रम ( $$$10 100 110 110$ ) पैटर्न के बारे में सभी आवश्यक जानकारी शामिल है। इसके साथ, हम मूल पैटर्न को पुनर्स्थापित कर सकते हैं (और पैटर्न की निचली सीमा से परे भी देख सकते हैं)। पक्षों के साथ एक वर्ग लें $$$एम$ । हम अपने अनुक्रम के बिट्स को उन जगहों पर व्यवस्थित करते हैं जहां गेंद ऊपरी दीवार से टकराती है (गेंद के निकटवर्ती स्पर्शों के बीच की दूरी 2 कोशिकाएं होती हैं)।



यदि संबंधित बिट = 1 - हम सेल के माध्यम से प्रक्षेपवक्र को चिह्नित करते हुए, बाईं ओर जाना शुरू करते हैं। यदि बिट = 0 - दाईं ओर ले जाएं।



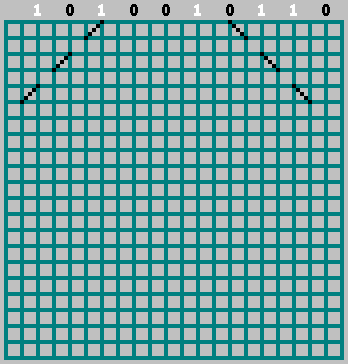
इस मामले में, शून्य बिट के बारे में मत भूलना:



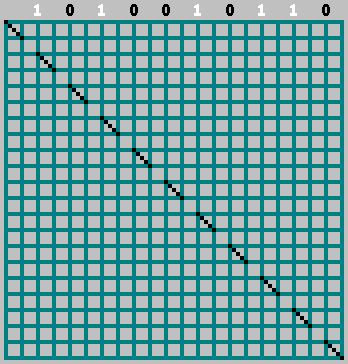
gif:



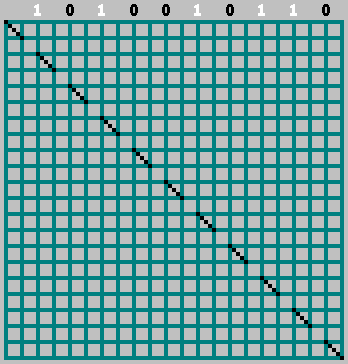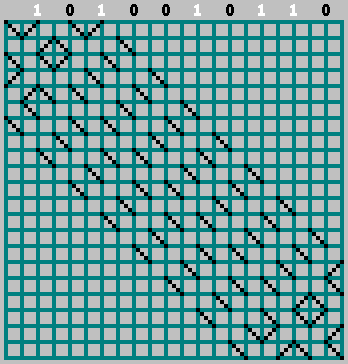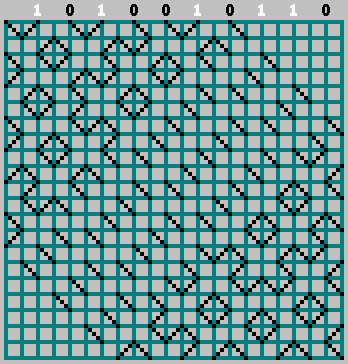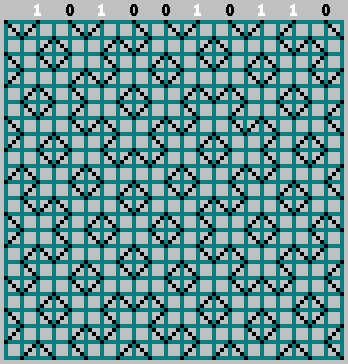
हमें मूल पैटर्न मिला (और निचली सीमा से थोड़ा परे देखा गया):



बाइनरी अनुक्रमों को देखने के लिए स्क्रिप्ट

शेष भाग का उपयोग करके हम इस अनुक्रम का निर्माण कर सकते हैं।

एक आयामी बिलियर्ड्स

संख्यात्मक धुरी पर $$$X$ दो बिंदु लें: $$$0$ और $$$एम$ ।



एक बिंदु से दूसरे तक बढ़ते हुए, दूरी को मापें $$$एन$ :



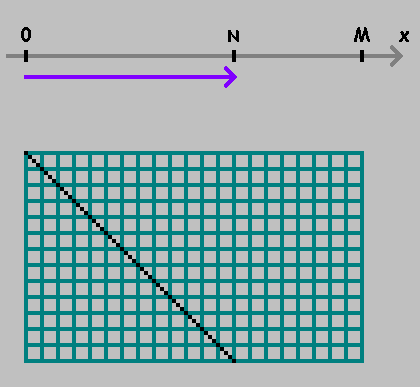
बिंदु को चिह्नित किया। हम दिशा को ध्यान में रखते हुए, इस बिंदु से दूरी को मापना जारी रखते हैं। अगर आप मुकाम तक पहुंच गए हैं $$$0$ या $$$एम$ - दिशा बदलें:



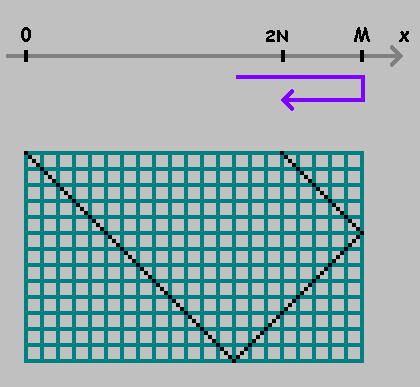
जैसा कि ऊपर दिए गए आंकड़ों में देखा जा सकता है, पहला बिंदु उस स्थान को दर्शाता है जहां गेंद बिलियर्ड्स की निचली दीवार को छूती है। यह बिंदु हमें रूचि नहीं देता है। हम केवल अंक तय करेंगे $$$2kN$ के लिए $$$k = 0,1,2, ...$ ।

इन बिंदुओं को कैसे चिह्नित करें? हमारे बिलियर्ड्स को अक्ष पर घुमाएं $$$X$ । अंक अंकित करें $$$0, M, 2M, 3M, ...$ । अब बात पहुंच रही है $$$एम$ हम आंदोलन की दिशा नहीं बदलते हैं, लेकिन इस बिंदु पर चलते रहते हैं $$$2M$ ।



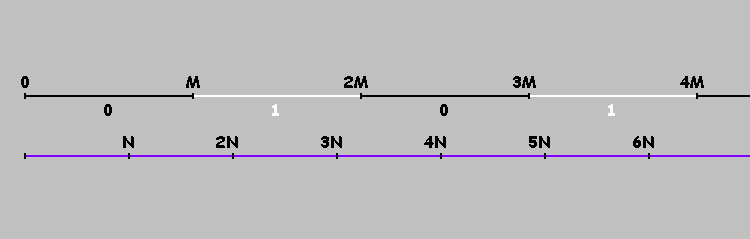
अंक कि गुणज हैं $$$एम$ हमारी धुरी को खंडों में विभाजित करें। हम सशर्त रूप से इन खंडों को शून्य और शून्य (वैकल्पिक) के साथ चिह्नित करते हैं। शून्य से चिह्नित खंडों पर, गेंद (एक आयताकार बिलियर्ड में) बाएं से दाएं चलती है। इकाइयों के साथ चिह्नित खंडों पर - दाएं से बाएं। या सरल: गेंद बाएँ से दाएँ चलती है अगर $$$Q_k = 0$ के लिए

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

(इस सूत्र पर विशेष ध्यान दिया जाना चाहिए। इसके बाद, हम इस पर लौटेंगे)

यह देखना आसान है कि जिस बिंदु पर गेंद बिलियर्ड्स की शीर्ष दीवार को छूती है वह विभाजन का शेष भाग है $$$2kN$ पर $$$एम$ । उसी समय, हम विपरीत दिशा में चलती हुई गेंद को रिकॉर्ड नहीं कर सकते। हम विभाजन का पूरा हिस्सा लेते हैं $$$2kN$ पर $$$एम$ अगर यह सम्‍मिलित है - हम शेष विभाजन पर विचार करते हैं $$$2kN$ पर $$$एम$ । 2 से परिणामी शेष को विभाजित करें (संपर्क के आसन्न बिंदुओं के बीच की दूरी दो कोशिकाएं हैं)। सरणी के तत्वों के सूचक मिलते हैं, जिन्हें हमें शून्य से भरना होगा। शेष तत्व इकाइयों से भरे हुए हैं (गेंद दाएं दीवार से बाईं ओर स्थानांतरित की गई है)।

अनुक्रम लंबाई = $$$\ frac {M} {2}$ ।

function sequence(m,n){ var md=m/2; var array=[]; for(var k=0;k<md;k++) array[k]=1; for(var k=0;k<md;k++) if(Math.floor(2*k*n/m)%2==0) array[((2*k*n)%m)/2]=0; return array; } console.log(sequence(55, 34).join('')); // -> 0101001011010010110101101001 

अब हम किसी भी पक्ष के साथ बिलियर्ड्स के लिए एक द्विआधारी अनुक्रम बना सकते हैं $$$एम$ और $$$एन$ (प्राकृतिक संख्या द्वारा)।
कुछ उदाहरण:
144x89 (फाइबोनैचि संख्या):
010100101101001011010110100101101001010010110100101101011010010110100101

169x70 (पेल नंबर):
0101011010100101011010100101011010110101001010110101001010110101001010010101101010010

233x55 (विषम फाइबोनैचि संख्या $$$F_n$ और $$$F_ {n-3}$ ):
0100100110110110010011011011001001001101100100100110110010010011011011001001101101100
10010011011001001001101100100100


हमारे पास सीक्वेंस हैं। आप बाइनरी दृश्यों की कल्पना कैसे कर सकते हैं? कछुए ग्राफिक्स का उपयोग करना।

कछुआ ग्राफिक्स

एक रेखा खींचें। अगला, हम अपने अनुक्रम से बारी-बारी से बिट्स लेते हैं। यदि बिट = 1 - पिछले एक के सापेक्ष खंड को चालू करें $$$60 ^ {\ circ}$ (दक्षिणावर्त)। यदि बिट = 0 - सेगमेंट को चालू करें $$$-60 ^ {\ circ}$ । अगले खंड की शुरुआत पिछले एक का अंत है।



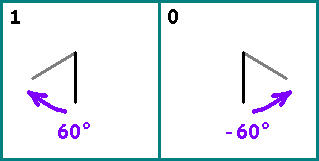
दो बड़े पर्याप्त फाइबोनैचि संख्याएँ लें: $$$F_ {29} = 514229$ और $$$F_ {28} = 317811$ ।

निर्मित अनुक्रम:
00101101001011010010100101101001011010110100101101001010010110100101 ... (257114 अक्षर प्लस शून्य बिट)।

हम कछुए ग्राफिक्स का उपयोग करते हुए कल्पना करते हैं। प्रारंभिक खंड का आकार 10 पिक्सेल है (निचले दाएं कोने में प्रारंभिक खंड):



प्रारंभिक खंड का आकार 5 पिक्सेल है:



प्रारंभिक खंड का आकार 1 पिक्सेल है:



अगला उदाहरण पेल नंबर है।

$$

$$P_n = \ start {case} 0, n = 0; \\ 1, n = 1 \\ 2P_ {n-1} + P_ {n-2}, n> 1 \ अंत {केस}$$

लेना $$$P_ {16} = 470832$ और $$$P_ {15} = 195025$ ।

अनुक्रम:
00101001010101010101010101010101010101010101010101000010101101 (235415 अक्षर प्लस शून्य बिट)।

प्रारंभिक खंड का आकार 1 पिक्सेल है:



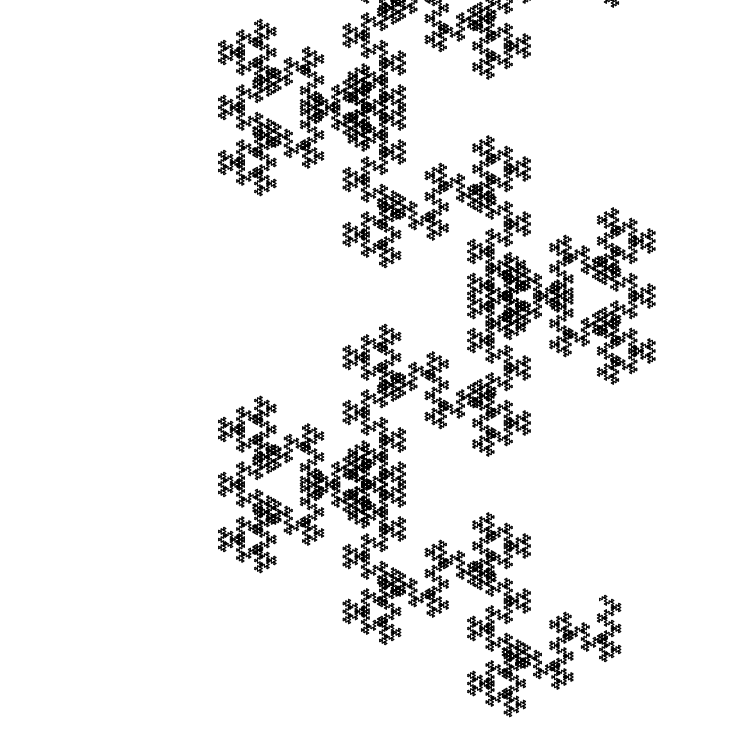
एक और उदाहरण विषम फाइबोनैचि संख्या है $$$F_n$ और $$$F_ {n-3}$ ।
लेना $$$F_ {28} = 317811$ और $$$F_ {25} = 75025$ ।
अनुक्रम:
00110110010010011111001001001001001101101100100110110110010011011011001001 ... (158905 प्लस शून्य बिट)।
कोनों के बजाय $$$60 ^ {\ circ}$ और $$$-60 ^ {\ circ}$ हम कोनों का उपयोग करेंगे $$$90 ^ {\ circ}$ और $$$-90 ^ {\ circ}$ ।
प्रारंभिक खंड का आकार 5 पिक्सेल है:



प्रारंभिक खंड का आकार 0.4 पिक्सेल है:



इस वक्र का एक नाम है - " फाइबोनैचि शब्द भग्न "। इस वक्र के लिए हॉसडॉर्फ आयाम ज्ञात है:

$$

$$D = 3 {\ frac {\ log \ Phi} {\ log (1 + {\ sqrt {2}}}}} = 1,6379; \ Quad \ Phi = \ frac {1 + {\ sqrt {5}}} {2}$$

कछुए ग्राफिक्स का उपयोग कर द्विआधारी दृश्यों को देखने के लिए स्क्रिप्ट

समस्या

क्या बिलियर्ड्स के लिए एक पैटर्न तैयार करना संभव है, जिनके पक्ष असंगत हैं (पक्षों में से एक एक अपरिमेय संख्या है)? कार्य तुच्छ नहीं है। इस समस्या को हल करने की कोशिश करते हुए, हम कई सवालों का सामना करेंगे:

1. यदि पार्टियां असंगत हैं - तो हम एक ही आकार के सेल वाले बिलियर्ड्स को प्रशस्त नहीं कर सकते।
2. यदि पक्ष असंगत हैं - तो गेंद असीम रूप से परावर्तित होगी और कोने से कभी नहीं टकराएगी।
3. बिलियर्ड्स में अनुक्रम क्रम में नहीं, बल्कि अनियमित रूप से भरे जाते हैं।



स्पष्ट रूप से पहले दो प्रश्नों का कोई हल नहीं है। लेकिन अगर अनुक्रम को क्रम में भरने का कोई तरीका था, तो हम अनुक्रम को बाएं से दाएं तरफ ले जा सकते हैं, पैटर्न को ऊपर के तरीके से बहाल कर सकते हैं जो हमने ऊपर उपयोग किया था। और यह देखने के लिए कि बिलियर्ड्स के ऊपरी बाएं कोने में पैटर्न कैसा दिखता है, जिसके किनारे असंगत हैं।

काला जादू

बिलियर्ड्स लें, जिनकी भुजाएँ फाइबोनैचि संख्याओं के बराबर हों (अन्य संख्याओं के साथ, ऐसी चाल काम नहीं कर सकती है)। इसमें गेंद को चलाएँ और ऊपरी दीवार को छूने वाली गेंद की संख्या को ठीक करें। संख्याओं को सफेद रंग से भरें - यदि गेंद दाएं से बाएं और काले में चली जाती है - यदि गेंद बाएं से दाएं तरफ जाती है:



सफेद रंग अनुक्रम में एक से मेल खाता है, काला - शून्य। अब क्रम में संख्याओं की व्यवस्था करते हैं:



हम लोगों और शून्य का बिल्कुल यही क्रम मिला।


वास्तव में, कुछ मामलों में, हमें शेष भाग लेने की आवश्यकता नहीं है। फाइबोनैचि संख्याओं के लिए, यह विभाजन के पूर्णांक भाग की समता की जांच करने के लिए पर्याप्त है $$$2kN$ पर $$$एम$ :

$$

$$Q_k = \ lfloor \ frac {2kN} {M} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

अंश में हमारे पास है $$$F_ {n}$ । हर में - $$$F_ {n + 1}$ ।

जैसा कि आप जानते हैं:

$$

$$\ lim_ {n \ _ to \ infty} \ frac {F_n} {F_ {n + 1}} = \ frac {1} {\ Phi}$$

$$$\ Phi$ - स्वर्णिम अनुपात। अपरिमेय संख्या। अब हम अपना सूत्र इस प्रकार लिख सकते हैं:

$$

$$Q_k = \ lfloor \ frac {2k} {\ Phi} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

हमें एक सूत्र मिला है जिसके द्वारा हम क्रम में बिलियर्ड्स के लिए अनुक्रम भर सकते हैं, जिसकी चौड़ाई बराबर है $$$\ Phi$ और ऊंचाई $$$1$ । अनुक्रम लंबाई = $$$\ infty$ , लेकिन हम पैटर्न के हिस्से को पुनर्स्थापित कर सकते हैं, बाएं से दाएं क्रम में आगे बढ़ रहे हैं और बिलियर्ड्स के ऊपरी बाएं कोने में देख सकते हैं। यह पता लगाना बाकी है कि गिनती कैसे की जाती है $$$\ Phi$

सुनहरे अनुपात द्वारा विभाजित इकाई को फिर से लिखा जा सकता है:

$$

$$\ frac {1} {\ Phi} = \ frac {-1 + {\ sqrt {5}}} {2}$$

हम दो से छुटकारा पा सकते हैं:

$$

$$\ frac {2k} {\ Phi} = \ frac {2k (-1 + {\ sqrt {5}}}} {2} = k \ sqrt {5} -k$$

हमारा सूत्र फार्म लेता है:

$$

$$Q_k = \ lfloor k \ sqrt {5} -k \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

स्पष्टता के लिए, मैंने एक तालिका खींची। तीसरे कॉलम में, हम भिन्नात्मक भाग को छोड़ देते हैं और पूरा छोड़ देते हैं। चौथे कॉलम में, हम पूर्णांक भाग की समता की जाँच करते हैं:



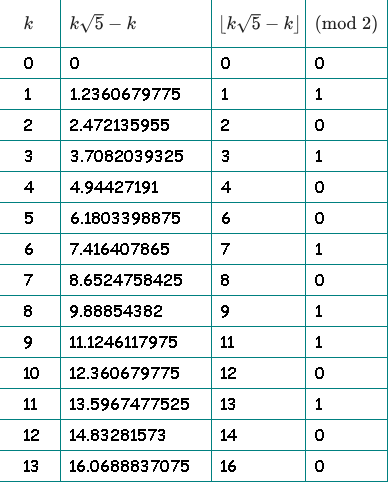
चौथे कॉलम में हमें हमारा अनुक्रम मिला: 01010010110100 ...

हम बाकी के लिए बिट्स की गणना करना जारी रखते हैं $$$k$ । पक्षों के साथ बिलियर्ड पैटर्न का हिस्सा बहाल करना $$$1$ और $$$\ Phi$ :



यदि आप हर बार नहीं ले जाते हैं $$$k$ - फिर अनुक्रम में हर दूसरा बिट उल्टा होता है। हम सामान्य सूत्र प्राप्त करते हैं:

$$

$$Q_k = \ lfloor k \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2); \ quad k = 0,1,2, ...$$

हमें पाँच के वर्गमूल के बजाय दो के वर्गमूल का प्रयोग करने से रोकता है या कहें? कोई बात नहीं।

हम एक अनुक्रम का निर्माण करते हैं $$$k \ sqrt {3} + k$

 var x=3; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x)+k)%2; 

अनुक्रम के पहले कुछ बिट्स:
00100101101001001011010010110110101010100001011010010010110100101 ...

हम कछुए ग्राफिक्स का उपयोग करके कल्पना करेंगे। 90 और -90 डिग्री के कोण। प्रारंभिक खंड का आकार 5 पिक्सेल है:



प्रारंभिक खंड का आकार 0.5 पिक्सेल है:



हम एक अनुक्रम का निर्माण करते हैं $$$k \ sqrt {2}$

 var x=2; var q=[]; for(var k=0;k<256000;k++) q[k]=Math.floor(k*Math.sqrt(x))%2; 

अनुक्रम के पहले कुछ बिट्स ( A083035 ):
0100110110010011001001111011001101100100110110011011001001100100110110 ...

90 और -90 डिग्री के कोण। प्रारंभिक खंड का आकार 5 पिक्सेल है:



प्रारंभिक खंड का आकार 0.5 पिक्सेल है:





60 और -60 डिग्री के कोण। प्रारंभिक खंड का आकार 5 पिक्सेल है:



दृश्य स्क्रिप्ट

किसी को संदेह हो सकता है कि पूर्णांक के हिस्से की समता $$$k \ sqrt {2}$ एक भग्न अनुक्रम देता है। हम दूसरे तरीके से इस क्रम के भाग की कल्पना करते हैं:



स्पष्टता के लिए, मैंने परिणामस्वरूप पैटर्न में सबसे लंबे वक्र पर पेंट किया:



इस वक्र का एक नाम है - "फाइबोनैचि शब्द भग्न"।

बिलियर्ड्स का उपयोग करके यह क्रम कैसे प्राप्त करें? हम बिलियर्ड लेते हैं, जिसकी चौड़ाई = 1 और ऊंचाई = है $$$\ sqrt {2}$ । ऊपरी और निचले सीमाओं पर, हम गेंद की गति की दिशा तय करते हैं। यदि गेंद बाएँ से दाएँ चलती है - 0 लिखें, यदि दाएँ से बाएँ - लेखन 1।



दो रेखांकन:

$$

$$z = \ lfloor y \ sqrt {x} \ rfloor \; (\ textrm {mod} \; 2)$$

$$

$$z = \ lfloor yx \ sqrt {2} \ rfloor \; (\ textrm {mod} \; 2)$$

आप इस नस में बहुत लंबे समय तक जारी रख सकते हैं - पैटर्न में कई दिलचस्प गुण हैं। लेकिन लेख पहले से ही बहुत बोझिल था। मैं अंत में दिलचस्प गुणों में से एक के बारे में बताऊंगा।