परिचय
Habr पर कई लेख [1,2,3] प्रकाशित किए गए हैं जो प्रत्यक्ष या अप्रत्यक्ष रूप से इस विषय से संबंधित हैं। इस संबंध में, कोई प्रकाशन [1] शीर्षक के साथ "गणित पर अंकन: रैखिक-द्विघात नियामक" को नोट करने में विफल हो सकता है, जो कि इष्टतम LQR नियंत्रक के संचालन के सिद्धांत को लोकप्रिय रूप से बताता है।
मैं इस विषय को जारी रखना चाहता था, जिसने डायनेमिक ऑप्टिमाइज़ेशन विधि के व्यावहारिक अनुप्रयोग की जांच की, लेकिन पहले से ही पायथन का उपयोग करके एक ठोस उदाहरण पर। सबसे पहले, शब्दावली और गतिशील अनुकूलन की विधि के बारे में कुछ शब्द।
अनुकूलन विधियों को स्थिर और गतिशील में विभाजित किया गया है। नियंत्रण वस्तु विभिन्न बाहरी और आंतरिक कारकों के प्रभाव में निरंतर आंदोलन की स्थिति में है। इसलिए, नियंत्रण परिणाम का मूल्यांकन नियंत्रण समय टी के लिए दिया गया है, और यह गतिशील अनुकूलन का कार्य है।
गतिशील अनुकूलन के तरीकों का उपयोग करते हुए, एक निश्चित अवधि में सीमित संसाधनों के वितरण से जुड़ी समस्याओं को हल किया जाता है, और उद्देश्य फ़ंक्शन को एक अभिन्न कार्यात्मक के रूप में लिखा जाता है।
इस तरह की समस्याओं को हल करने के लिए गणितीय उपकरण परिवर्तनशील विधियां हैं: विविधताओं का शास्त्रीय कलन, अधिकतम एल.एस. का सिद्धांत। पोंट्रीगिन और गतिशील प्रोग्रामिंग आर बेलमैन।
नियंत्रण प्रणालियों का विश्लेषण और संश्लेषण समय, आवृत्ति और राज्य के स्थानों में किया जाता है। राज्य अंतरिक्ष में नियंत्रण प्रणालियों के विश्लेषण और संश्लेषण को पाठ्यक्रम में पेश किया जाता है, हालांकि, SQR नियंत्रक का उपयोग करते हुए प्रशिक्षण सामग्री में प्रस्तुत तकनीक को मटलब का उपयोग करने के लिए डिज़ाइन किया गया है और इसमें विश्लेषण के व्यावहारिक उदाहरण नहीं हैं।
इस प्रकाशन का उद्देश्य राज्य अंतरिक्ष में रैखिक नियंत्रण प्रणालियों के विश्लेषण और संश्लेषण के तरीकों पर विचार करना है, जो इलेक्ट्रिक ड्राइव के नियंत्रण प्रणाली और पायथन प्रोग्रामिंग भाषा का उपयोग करते हुए एक विमान के अनुकूलन के प्रसिद्ध उदाहरण का उपयोग करता है।
गतिशील अनुकूलन विधि का गणितीय अनुमान
अनुकूलन के लिए, आयाम (एमओ), सममित (सीओ) और समझौता ऑप्टिमम (केओ) के मानदंडों का उपयोग किया जाता है।
राज्य स्थान में अनुकूलन समस्याओं को हल करते समय, वेक्टर - मैट्रिक्स समीकरणों द्वारा एक रेखीय स्थिर प्रणाली दी जाती है:
x= fracdxdt=A cdotx+B cdotu;y=C cdotx, (1)
न्यूनतम नियंत्रण ऊर्जा खपत और अधिकतम गति के लिए अभिन्न मानदंड फंक्शनल द्वारा निर्धारित किए गए हैं:
Jx= int infty0(xTQx+uTRu+2xTNu)dt rightarrowmin, (2)
Ju= int infty0(yTQy+uTRu+2yTNu)dt rightarrowmin। (3)
नियंत्रण कानून यू राज्य चर x या आउटपुट चर y पर रैखिक प्रतिक्रिया के रूप में है:
u= pmKx,u= pmKyऐसा नियंत्रण द्विघात गुणवत्ता मानदंड (2), (3) को कम करता है। संबंधों में (1) ÷ (3), क्यू और आर क्रमशः आयाम [n × n] और [m × m] के सममित सकारात्मक निश्चित मैट्रिक्स हैं; K आयाम के निरंतर गुणांक का एक मैट्रिक्स है [m × n], जिसके मूल्य सीमित नहीं हैं। यदि इनपुट पैरामीटर एन छोड़ा गया है, तो इसे शून्य माना जाता है।
इस समस्या का समाधान, जिसे रैखिक अभिन्न द्विघात अनुकूलन (LQR- अनुकूलन) समस्या कहा जाता है, राज्य अंतरिक्ष में अभिव्यक्ति द्वारा निर्धारित किया जाता है:
u=R−1BTPxजहां मैट्रिक्स P को रिकेटी समीकरण को संतुष्ट करना चाहिए:
ATP+PA+PBR−1BTP+Q=0मानदंड (2), (3) भी विरोधाभासी हैं, क्योंकि पहले कार्यकाल के कार्यान्वयन के लिए असीम रूप से उच्च शक्ति के स्रोत की आवश्यकता होती है, और दूसरे के लिए, असीम रूप से कम शक्ति के स्रोत की आवश्यकता होती है। इसे निम्नलिखित अभिव्यक्ति द्वारा समझाया जा सकता है:
Jx= int infty0xTQxdt ।
जो आदर्श है
मॉड(x) वेक्टर x, अर्थात विनियमन की प्रक्रिया में इसके दोलन का एक उपाय है, और इसलिए, कम दोलन के साथ तेजी से संक्रमण में छोटे मान लेता है, और अभिव्यक्ति:
Ju= int infty0uTRudtनियंत्रण के लिए उपयोग की जाने वाली ऊर्जा की मात्रा का एक माप है, यह सिस्टम की ऊर्जा लागतों के लिए एक दंड है।
वजन क्यू, आर, और एन इसी निर्देशांक की बाधाओं पर निर्भर करता है। यदि इन मेट्रिसेस का कोई तत्व शून्य के बराबर है, तो संबंधित समन्वय में कोई प्रतिबंध नहीं है। व्यवहार में, मैट्रिस क्यू, आर, एन के मूल्यों का चुनाव विशेषज्ञ अनुमानों, परीक्षणों, त्रुटियों की विधि द्वारा किया जाता है और डिजाइन इंजीनियर के अनुभव और ज्ञान पर निर्भर करता है।
ऐसी समस्याओं को हल करने के लिए, निम्नलिखित MATLAB ऑपरेटरों का उपयोग किया गया था:
startbmatrixR,S,E endbmatrix=lqr(A,B,Q,R,N) और
startbmatrixR,S,E endbmatrix=lqry(Ps,Q,R,N) राज्य वेक्टर x या आउटपुट वेक्टर y द्वारा कार्यात्मक (2), (3) को कम करें।
प्रबंधन ऑब्जेक्ट मॉडल
Ps=ss(ए,बी,सी,डी) गणना का परिणाम राज्य चर x, रिक्ट्टी समीकरण S के समाधान और बंद लूप नियंत्रण प्रणाली के eigenvalues E = eiq (A-BK) के संबंध में इष्टतम प्रतिक्रियाओं का मैट्रिक्स K है।
कार्यात्मक घटक:
Jx=x0TP1x0,Ju=x0TP2x0जहां x0 प्रारंभिक स्थितियों का वेक्टर है;
P1 और
P2 - अज्ञात मैट्रिसेस जो कि ल्यपुनोव मैट्रिक्स समीकरणों का एक समाधान है। वे कार्यों का उपयोग करते हुए पाए जाते हैं;
P1=lyap(NN,Q) और
P2=lyap(NN,KTRK) ।
एनएन=(ए+बीके)टीपायथन का उपयोग करके गतिशील अनुकूलन विधि के कार्यान्वयन की विशेषताएं
यद्यपि पायथन कंट्रोल सिस्टम्स लाइब्रेरी [4] के कार्य हैं: control.lqr, control.lyap, हालांकि, control.lqr का उपयोग केवल तभी संभव है जब slycot मॉड्यूल स्थापित हो, जो एक समस्या है [5]। किसी कार्य के संदर्भ में गीत समारोह का उपयोग करते समय, अनुकूलन एक control.exception.ControlArgument में परिणाम देता है: क्यू एक सममित मैट्रिक्स त्रुटि [6] होना चाहिए।
इसलिए, lqr () और lyap () फ़ंक्शन को लागू करने के लिए, मैंने scipy.linalg का उपयोग किया:
from numpy import* from scipy.linalg import* def lqr(A,B,Q,R): S =matrix(solve_continuous_are(A, B, Q, R)) K = matrix(inv(R)*(BT*S)) E= eig(AB*K)[0] return K, S, E P1=solve_lyapunov(NN,Ct*Q*C)
वैसे, आपको कार्य को पूरी तरह से नहीं छोड़ना चाहिए, क्योंकि फ़ंक्शन चरण (), पोल (), एसएस (), टीएफ (), फीडबैक (), एकर (), स्थान () और अन्य अच्छी तरह से काम करते हैं।
इलेक्ट्रिक ड्राइव में LQR ऑप्टिमाइज़ेशन का एक उदाहरण
(एक उदाहरण प्रकाशन से लिया गया है [7])एक रैखिक-द्विघात नियंत्रक के संश्लेषण पर विचार करें जो मैट्रेस द्वारा राज्य स्थान में परिभाषित नियंत्रण वस्तु के लिए मानदंड (2) को पूरा करता है:
A = \ start {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 \\ & 0 & 1.046 & 0 \ end {bmatrix}; b = \ start / bmatrix} 2300 \\ 0 \\ 0 \\\ अंत {bmatrix}; C = \ start {bmatrix} 1 & 0 & 0 \\ 0 & 1 & 0 \\ 0 & 0 & 1 \ end {bmatrix}; D = 0
निम्नलिखित को राज्य चर के रूप में माना जाता है:
x1 - कनवर्टर वोल्टेज, वी;
x2 - मोटर वर्तमान, ए;
x3 - कोणीय वेग
c−1 । यह एचपी के साथ टीपी - डीपीटी प्रणाली है: इंजन आर नॉम = 30 किलोवाट; यूनोम = 220 वी; इनोम = 147 ए;
omegaω 0 = 169
c−1 ;
omegaω अधिकतम = 187
c−1 ; नाममात्र प्रतिरोध क्षण Mnom = 150 N * m; वर्तमान = 2 शुरू करने की बहुलता; thyristor कनवर्टर: Unom = 230 V; उई = 10 बी; इनोम = 300 ए; शॉर्ट-टाइम ओवरक्रॉफ्ट की बहुलता = 1.2।
समस्या को हल करते समय, हम मैट्रिक्स Q विकर्ण को स्वीकार करते हैं। मॉडलिंग के परिणामस्वरूप, यह पाया गया कि मैट्रिक्स तत्वों का न्यूनतम मान R = 84, और
Q=[[0.01,0,0],[0,0.01,0],[0,0,0.01]] इस मामले में, इंजन के कोणीय वेग की एक मोनोटोनिक संक्रमण प्रक्रिया देखी जाती है (छवि 1)। आर = 840 पर
Q=[[0.01,0,0],[0,0.01,0],[0,0,0.01]] क्षणिक प्रक्रिया (छवि 2) एमओ के मानदंडों को पूरा करती है। मैट्रिक्स P1 और P2 की गणना x0 = [220 147 162] पर की गई थी।
कार्यक्रम की सूची (चित्र 1)। 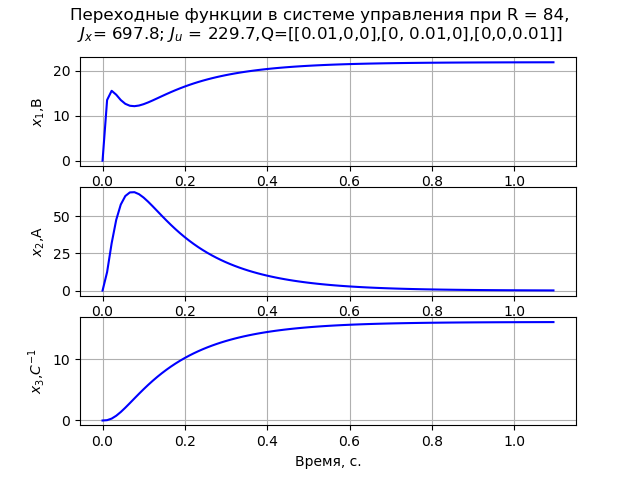 अंजीर। 1
अंजीर। 1कार्यक्रम की सूची (चित्र 2)। 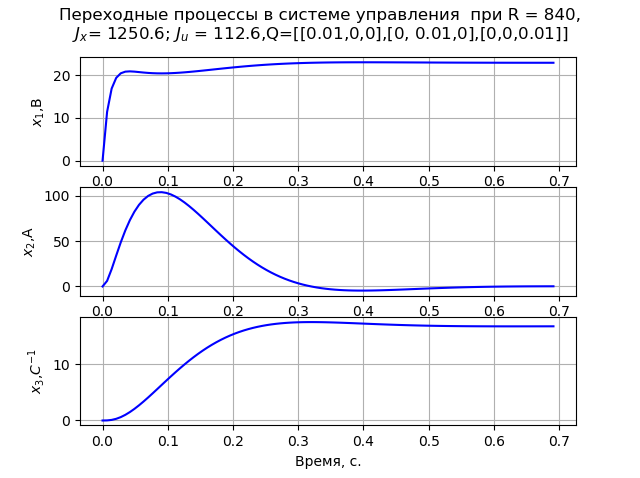 अंजीर। 2
अंजीर। 2मेट्रिस आर और क्यू के उपयुक्त चयन से, मोटर के शुरुआती प्रवाह को स्वीकार्य मानों के बराबर कम करना संभव है (2-2.5) इन (छवि 3)। उदाहरण के लिए, आर = 840 और के साथ
Q = ([[[0.01,0,0]]], [0,0.88,0], [0,0,0.01]], इसका मूल्य 292 A है और इन परिस्थितियों में संक्रमण प्रक्रिया का समय 1.57 s है।
कार्यक्रम की सूची (चित्र 3)। 
3 चित्र
विचार किए गए सभी मामलों में, वोल्टेज और वर्तमान पर प्रतिक्रियाएं नकारात्मक हैं, और गति पर, सकारात्मक, जो स्थिरता की आवश्यकताओं के अनुसार अवांछनीय है। इसके अलावा, संश्लेषित प्रणाली कार्य के लिए आश्चर्यजनक है और लोड के लिए स्थिर है। इसलिए, हम एक अतिरिक्त राज्य चर के साथ राज्य अंतरिक्ष में एक पीआई नियंत्रक के संश्लेषण पर विचार करते हैं
x4 - इंटीग्रेटर का स्थानांतरण गुणांक।
हम मैट्रिसेस के रूप में प्रारंभिक जानकारी का प्रतिनिधित्व करते हैं:
A = \ start {bmatrix} & -100 & 0 & 0 \\ & 143.678 & -16.667 & -195.402 & 0 \\ & 0 & 1.046 & 0 & 0 \\ & 0 & 1 & 0 & 1 & 0 \ अंत {bmatrix}; b = = \ start {bmatrix} 2300 \\ 0 \\ 0 \\ 0 \\\ end {bmatrix}; C = eye (4)); D = 0एमओ मानदंड के अनुरुप टास्क ट्रांजिस्टर R = 100, q11 = q22 = q33 = 0.001 और q44 = 200 पर प्राप्त किए गए थे। चित्र 4 राज्य के वैरिएबल ट्रांजिस्टर को दर्शाता है जो कार्य द्वारा और लोड के द्वारा सिस्टम के एस्टैटिज़्म की पुष्टि करता है।
कार्यक्रम लिस्टिंग (छवि 4)। 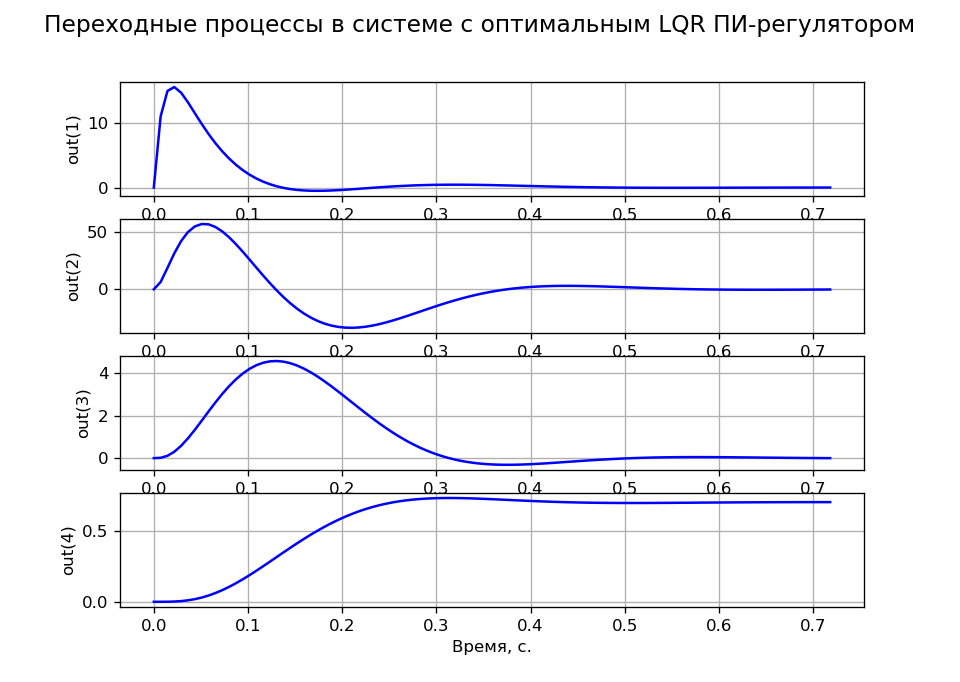 अंजीर। 4
अंजीर। 4मैट्रिक्स K को निर्धारित करने के लिए, पायथन कंट्रोल सिस्टम लाइब्रेरी के दो कार्य हैं K = acker (A, B, s) और K = स्थान (A, B, s), जहां s वेक्टर है - बंद-लूप नियंत्रण प्रणाली के हस्तांतरण समारोह के वांछित ध्रुवों की पंक्ति। पहला कमांड केवल n with5 के लिए यू में एक इनपुट वाले सिस्टम के लिए उपयोग किया जा सकता है। दूसरे के पास इस तरह के प्रतिबंध नहीं हैं, लेकिन ध्रुवों की बहुलता मैट्रिक्स बी के रैंक से अधिक नहीं होनी चाहिए। एकर () ऑपरेटर का उपयोग करने का एक उदाहरण लिस्टिंग में और (छवि 5) में दिखाया गया है।
कार्यक्रम लिस्टिंग (छवि 5)।  अंजीर। 5
अंजीर। 5निष्कर्ष
प्रकाशन में प्रस्तुत LQR- ड्राइव ऑप्टिमाइज़ेशन का कार्यान्वयन, नए lqr () और lyap () फ़ंक्शन का उपयोग करते हुए, हमें नियंत्रण सिद्धांत के संबंधित अनुभाग का अध्ययन करते समय लाइसेंस प्राप्त MATLAB प्रोग्राम के उपयोग को छोड़ने की अनुमति देगा।
एक विमान में एलक्यूआर अनुकूलन का एक उदाहरण (एलए)
(एक उदाहरण एस्ट्रो और मृरेय द्वारा प्रकाशन से लिया गया है, अध्याय 5 [8] और लेख के लेखक द्वारा अंतिम रूप से lqr () फ़ंक्शन को बदलने और शब्दावली को कम करने के संदर्भ में अंतिम रूप से स्वीकार किया जाता है)सैद्धांतिक भाग, एक संक्षिप्त सिद्धांत, एलक्यूआर अनुकूलन को पहले ही ऊपर माना जा चुका है, इसलिए आइए कोड विश्लेषण पर इसी टिप्पणी के साथ आगे बढ़ें:
आवश्यक पुस्तकालयों और LQR नियंत्रक फ़ंक्शन। from scipy.linalg import*
प्रारंभिक स्थिति और बुनियादी मैट्रिक्स ए, बी, सी, डी मॉडल। xe = [0, 0, 0, 0, 0, 0];
हम xy स्थिति में चरण-दर-चरण परिवर्तनों के अनुरूप इनपुट और आउटपुट का निर्माण करते हैं। वैक्टर xd और yd सिस्टम में वांछित स्थिर अवस्था के अनुरूप हैं। Matrices Cx और Cy मॉडल के संबंधित आउटपुट हैं। सिस्टम की गतिशीलता का वर्णन करने के लिए, हम वेक्टर-मैट्रिक्स समीकरणों की एक प्रणाली का उपयोग करते हैं:
\ बाईं \ {\ _ शुरू करें {मैट्रिक्स} xdot = Ax + Bu => xdot = (A-BK) x + xd \\ u = -K (x-xd) \\ y = Cx \\ \ end {मैट्रिक्स} \ सही।
बंद लूप की गतिशीलता को चरण () फ़ंक्शन का उपयोग करके मॉडलिंग किया जा सकता है, इनपुट वैक्टर के रूप में K \ cdot xd और K \ cdot xd के लिए, जहां:
xd = matrix([[1], [0], [0], [0], [0], [0]]); yd = matrix([[0], [1], [0], [0], [0], [0]]);
वर्तमान नियंत्रण 0.8.1 पुस्तकालय प्रतिक्रिया नियंत्रकों को बनाने के लिए SISO Matlab फ़ंक्शंस के केवल भाग का समर्थन करता है, इसलिए, नियंत्रक से डेटा को पढ़ने के लिए, इसलिए पार्श्व -x और ऊर्ध्वाधर -y डायनेमिक्स के लिए इंडेक्स वैक्टर lat (), alt () बनाना आवश्यक है।
lat = (0,2,3,5); alt = (1,4);
प्रत्येक कार्य के लिए एक-एक करके शेड्यूल का निष्कर्ष।
figure(); title(" x y") plot(Tx.T, Yx.T, '-', Ty.T, Yy.T, '--'); plot([0, 10], [1, 1], 'k-'); axis([0, 10, -0.1, 1.4]); ylabel(' '); xlabel(''); legend(('x', 'y'), loc='lower right'); grid() show()
अनुसूची: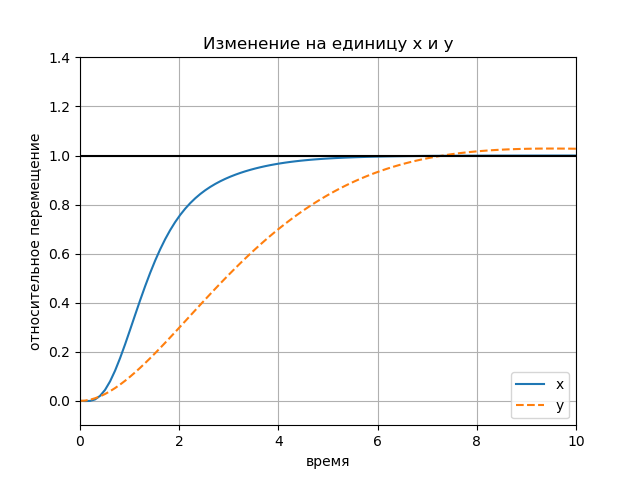
इनपुट क्रियाओं के आयाम का प्रभाव अनुसूची: अनुसूची:
अनुसूची: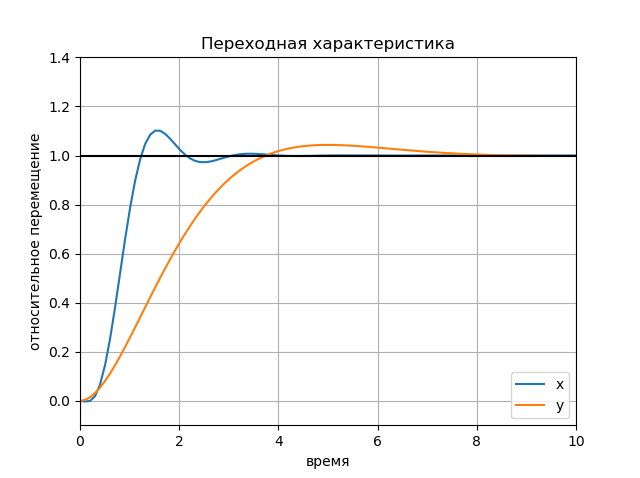
शारीरिक रूप से क्षणिक प्रतिक्रिया अनुसूची: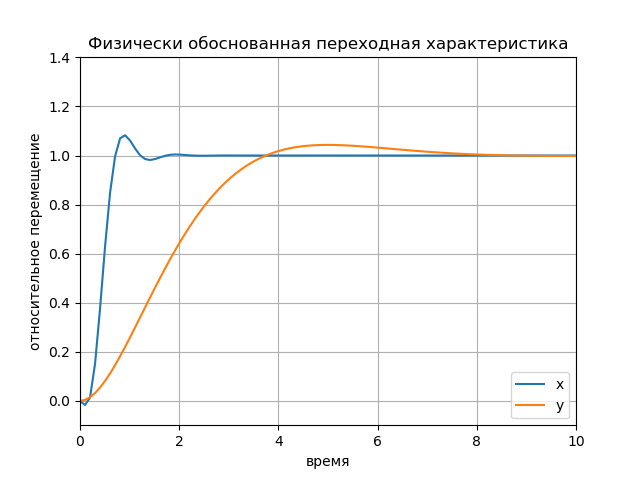
निष्कर्ष:
प्रकाशन में प्रस्तुत विमान में LQR अनुकूलन के कार्यान्वयन, नए lqr () फ़ंक्शन के उपयोग को ध्यान में रखते हुए, हमें नियंत्रण सिद्धांत के संबंधित अनुभाग का अध्ययन करते समय लाइसेंस प्राप्त कार्यक्रम MATLAB के उपयोग को छोड़ने की अनुमति देगा।
संदर्भ
1.
उंगलियों पर गणित: रैखिक-द्विघात नियंत्रक।2.
इष्टतम नियंत्रण प्रणाली को डिजाइन करने की समस्याओं में राज्य का स्थान।3.
स्वचालित नियंत्रण प्रणाली को डिजाइन करने के लिए पायथन कंट्रोल सिस्टम लाइब्रेरी का उपयोग करना।4.
पायथन कंट्रोल सिस्टम लाइब्रेरी।5.
पायथन - स्पायडर (RuntimeError & ImportError) में slycot मॉड्यूल आयात नहीं कर सकता।6.
पायथन कंट्रोल सिस्टम लाइब्रेरी।7.
एक इलेक्ट्रिक ड्राइव में इष्टतम नियंत्रण और lrr अनुकूलन के लिए मानदंड।