तंत्रिका साधारण विभेदक समीकरण
अंतर समीकरणों द्वारा प्रक्रियाओं का एक महत्वपूर्ण अनुपात वर्णित है, यह समय के साथ भौतिक प्रणाली का विकास, रोगी की चिकित्सा स्थिति, शेयर बाजार की मूलभूत विशेषताओं आदि हो सकता है। इस तरह की प्रक्रियाओं पर डेटा प्रकृति में लगातार और निरंतर हैं, इस अर्थ में कि अवलोकन केवल कुछ प्रकार के निरंतर बदलते राज्य की अभिव्यक्तियां हैं।
एक अन्य प्रकार का सीरियल डेटा भी है, यह असतत डेटा है, उदाहरण के लिए, एनएलपी टास्क डेटा। इस तरह के डेटा में स्थिति अलग-अलग होती है: एक चरित्र या शब्द से दूसरे में।
अब दोनों प्रकार के ऐसे सीरियल डेटा को आमतौर पर पुनरावर्ती नेटवर्क द्वारा संसाधित किया जाता है, हालांकि वे प्रकृति में भिन्न होते हैं और विभिन्न दृष्टिकोणों की आवश्यकता होती है।
पिछले
एनआईपीएस सम्मेलन में एक बहुत ही दिलचस्प लेख प्रस्तुत किया गया था, जो इस समस्या को हल करने में मदद कर सकता है। लेखक एक दृष्टिकोण का प्रस्ताव करते हैं जिसे उन्होंने
न्यूरल ओडीई कहा है।
यहाँ मैंने इस लेख के परिणामों को पुन: प्रस्तुत करने और संक्षेप में प्रस्तुत करने की कोशिश की ताकि उनके विचार से परिचित होना आसान हो सके। यह मुझे लगता है कि इस नए आर्किटेक्चर को अच्छी तरह से डेटा वैज्ञानिक के मानक उपकरणों में एक जगह मिल सकती है और साथ ही साथ आवर्ती नेटवर्क भी।
चित्रा 1: निरंतर ढाल backpropagation समय में संवर्धित अंतर समीकरण को हल करने की आवश्यकता है।
तीर टिप्पणियों से ग्रेडिएंट्स द्वारा पिछड़े प्रचारित ग्रेडिएंट्स के समायोजन का प्रतिनिधित्व करते हैं।
मूल लेख से चित्रण।
समस्या कथन
एक प्रक्रिया है जो कुछ अज्ञात ODE का पालन करती है और प्रक्रिया के प्रक्षेपवक्र के साथ कई (शोर) अवलोकन करते हैं
कैसे एक अनुमान लगाने के लिए

स्पीकर के कार्य

?
सबसे पहले, एक सरल कार्य पर विचार करें: केवल 2 अवलोकन हैं, शुरुआत में और प्रक्षेपवक्र के अंत में,

।
सिस्टम का विकास राज्य से शुरू होता है

समय पर

ODE सिस्टम के विकास के किसी भी तरीके का उपयोग करके कुछ पैरामीटर वाले डायनामिक्स फ़ंक्शन के साथ। सिस्टम के बाद एक नए राज्य में है

, यह राज्य के साथ तुलना की जाती है

और उनके बीच का अंतर मानकों को अलग करके कम से कम किया जाता है

गतिशीलता कार्य करता है।
या, औपचारिक रूप से, नुकसान फ़ंक्शन को कम करने पर विचार करें

:
को कम करने के लिए

, आपको इसके सभी मापदंडों के लिए ग्रेडिएंट की गणना करने की आवश्यकता है:

। ऐसा करने के लिए, आपको पहले यह निर्धारित करने की आवश्यकता है कि कैसे

हर पल राज्य पर निर्भर करता है

:

एक
सहायक राज्य कहा जाता है, इसकी गतिशीलता एक अन्य अंतर समीकरण द्वारा दी गई है, जिसे एक जटिल फ़ंक्शन (
श्रृंखला नियम ) के भेदभाव के एक निरंतर एनालॉग माना जा सकता है:
इस सूत्र का आउटपुट मूल लेख के परिशिष्ट में पाया जा सकता है।
इस आलेख में वैक्टर को लोअरकेस वैक्टर माना जाना चाहिए, हालांकि मूल लेख एक पंक्ति और स्तंभ प्रतिनिधित्व दोनों का उपयोग करता है।समय में अंतर (4) को हल करते हुए, हम प्रारंभिक अवस्था पर निर्भरता प्राप्त करते हैं

:
के संबंध में ढाल की गणना करने के लिए

और

, आप बस उन्हें राज्य का हिस्सा मान सकते हैं। इस स्थिति को
संवर्धित कहा जाता है। इस राज्य की गतिशीलता मूल गतिशीलता से तुच्छ रूप से प्राप्त होती है:
फिर इस संवर्धित राज्य के लिए संयुग्म राज्य:
धीरे संवर्धित गतिशीलता:
संयुग्मित संवर्धित अवस्था के अंतर समीकरण सूत्र से (4) तब:
समय सीमा में इस ODE को हल करना:
किसके साथ है
सभी इनपुट पैरामीटर्स में ग्रेडिएंट्स को
OESESolve ODE
solver देता है ।
सभी ग्रेडिएंट (१०), (११), (१२), (१३) को संयुग्मित संवर्धित अवस्था (९) की गतिकी के साथ एक
ओडीसॉल्व कॉल में एक साथ गणना की जा सकती है।
 मूल लेख से चित्रण।
मूल लेख से चित्रण।ऊपर दिए गए एल्गोरिदम क्रमिक टिप्पणियों के लिए ODE समाधान के ढाल के रिवर्स प्रसार का वर्णन करता है।
एक प्रक्षेपवक्र पर कई टिप्पणियों के मामले में, सब कुछ उसी तरह से गणना की जाती है, लेकिन टिप्पणियों के क्षणों में, प्रचारित ढाल के व्युत्क्रम को वर्तमान अवलोकन से ग्रेडिएंट के साथ समायोजित किया जाना चाहिए, जैसा कि
चित्र 1 में दिखाया गया है।
कार्यान्वयन
नीचे दिए गए कोड मेरे
तंत्रिका न्यूरॉज का कार्यान्वयन है। मैंने विशुद्ध रूप से यह समझने के लिए किया कि क्या हो रहा है। हालांकि, यह लेख के लेखकों के
भंडार में लागू होने के बहुत करीब है। इसमें वह सभी कोड होते हैं, जिन्हें आपको एक स्थान पर समझने की आवश्यकता होती है, यह थोड़ा और अधिक टिप्पणी करता है। वास्तविक अनुप्रयोगों और प्रयोगों के लिए, मूल लेख के लेखकों के कार्यान्वयन का उपयोग करना अभी भी बेहतर है।
import math import numpy as np from IPython.display import clear_output from tqdm import tqdm_notebook as tqdm import matplotlib as mpl import matplotlib.pyplot as plt %matplotlib inline import seaborn as sns sns.color_palette("bright") import matplotlib as mpl import matplotlib.cm as cm import torch from torch import Tensor from torch import nn from torch.nn import functional as F from torch.autograd import Variable use_cuda = torch.cuda.is_available()
सबसे पहले आपको ODE सिस्टम के विकास के लिए किसी भी विधि को लागू करने की आवश्यकता है। सादगी के लिए, यूलर पद्धति को यहां लागू किया गया है, हालांकि कोई भी स्पष्ट या निहित विधि उपयुक्त है।
def ode_solve(z0, t0, t1, f): """ - """ h_max = 0.05 n_steps = math.ceil((abs(t1 - t0)/h_max).max().item()) h = (t1 - t0)/n_steps t = t0 z = z0 for i_step in range(n_steps): z = z + h * f(z, t) t = t + h return z
यह उपयोगी तरीकों के एक जोड़े के साथ एक मानकीकृत डायनामिक्स फ़ंक्शन के सुपरक्लास का भी वर्णन करता है।
पहला: आपको उन सभी मापदंडों को वापस करने की आवश्यकता है जिन पर फ़ंक्शन वेक्टर के रूप में निर्भर करता है।
दूसरी बात: संवर्धित गतिशीलता की गणना करना आवश्यक है। यह गतिशीलता मापदंडों और इनपुट डेटा के संदर्भ में पैरामीटर किए गए फ़ंक्शन के ग्रेडिएंट पर निर्भर करती है। प्रत्येक नई वास्तुकला के लिए प्रत्येक हाथ से ढाल को पंजीकृत नहीं करने के लिए, हम
torch.autograd.grad विधि का उपयोग करेंगे।
class ODEF(nn.Module): def forward_with_grad(self, z, t, grad_outputs): """Compute f and a df/dz, a df/dp, a df/dt""" batch_size = z.shape[0] out = self.forward(z, t) a = grad_outputs adfdz, adfdt, *adfdp = torch.autograd.grad( (out,), (z, t) + tuple(self.parameters()), grad_outputs=(a), allow_unused=True, retain_graph=True )
नीचे दिए गए कोड में
तंत्रिका ODE के लिए आगे और पीछे के प्रसार का वर्णन है। आपको इस कोड को मुख्य
torch.nn.Module से
torch.autograd.Function फ़ंक्शन के रूप में
अलग करना होगा क्योंकि उत्तरार्द्ध में आप एक मॉड्यूल के विपरीत, एक मनमाना
backpropagation विधि को लागू कर सकते हैं। तो यह सिर्फ एक बैसाखी है।
यह सुविधा संपूर्ण
तंत्रिका ODE दृष्टिकोण को रेखांकित करती है।
class ODEAdjoint(torch.autograd.Function): @staticmethod def forward(ctx, z0, t, flat_parameters, func): assert isinstance(func, ODEF) bs, *z_shape = z0.size() time_len = t.size(0) with torch.no_grad(): z = torch.zeros(time_len, bs, *z_shape).to(z0) z[0] = z0 for i_t in range(time_len - 1): z0 = ode_solve(z0, t[i_t], t[i_t+1], func) z[i_t+1] = z0 ctx.func = func ctx.save_for_backward(t, z.clone(), flat_parameters) return z @staticmethod def backward(ctx, dLdz): """ dLdz shape: time_len, batch_size, *z_shape """ func = ctx.func t, z, flat_parameters = ctx.saved_tensors time_len, bs, *z_shape = z.size() n_dim = np.prod(z_shape) n_params = flat_parameters.size(0)
अब सुविधा के लिए, इस फ़ंक्शन को
nn.Module में
लपेटें ।
class NeuralODE(nn.Module): def __init__(self, func): super(NeuralODE, self).__init__() assert isinstance(func, ODEF) self.func = func def forward(self, z0, t=Tensor([0., 1.]), return_whole_sequence=False): t = t.to(z0) z = ODEAdjoint.apply(z0, t, self.func.flatten_parameters(), self.func) if return_whole_sequence: return z else: return z[-1]
आवेदन
वास्तविक गतिशीलता समारोह की पुनर्प्राप्ति (दृष्टिकोण सत्यापन)
एक बुनियादी परीक्षण के रूप में, आइए अब देखें कि क्या
तंत्रिका ODE अवलोकन संबंधी डेटा का उपयोग करके गतिशीलता के वास्तविक कार्य को पुनर्स्थापित कर सकता है।
ऐसा करने के लिए, हम पहले ODE के डायनामिक्स फ़ंक्शन को निर्धारित करते हैं, इसके आधार पर प्रक्षेपवक्र को विकसित करते हैं, और फिर इसे बेतरतीब ढंग से पैरामीटर किए गए डायनेमिक्स फ़ंक्शन से पुनर्स्थापित करने का प्रयास करते हैं।
सबसे पहले, हम एक रैखिक ODE के सबसे सरल मामले की जांच करते हैं। गतिकी का कार्य केवल एक मैट्रिक्स की क्रिया है।
एक यादृच्छिक मैट्रिक्स द्वारा प्रशिक्षित फ़ंक्शन पैराट्राइज्ड है।
इसके अलावा, थोड़ा और अधिक परिष्कृत गतिशीलता (जिफ के बिना, क्योंकि सीखने की प्रक्रिया इतनी सुंदर नहीं है :))
यहां सीखने का कार्य एक छिपी हुई परत के साथ पूरी तरह से जुड़ा हुआ नेटवर्क है।
कोड class LinearODEF(ODEF): def __init__(self, W): super(LinearODEF, self).__init__() self.lin = nn.Linear(2, 2, bias=False) self.lin.weight = nn.Parameter(W) def forward(self, x, t): return self.lin(x)
डायनामिक्स फ़ंक्शन केवल एक मैट्रिक्स है
class SpiralFunctionExample(LinearODEF): def __init__(self): matrix = Tensor([[-0.1, -1.], [1., -0.1]]) super(SpiralFunctionExample, self).__init__(matrix)
बेतरतीब ढंग से पैरामीटर मैट्रिक्स
class RandomLinearODEF(LinearODEF): def __init__(self): super(RandomLinearODEF, self).__init__(torch.randn(2, 2)/2.)
अधिक परिष्कृत प्रक्षेपवक्र के लिए गतिशीलता
class TestODEF(ODEF): def __init__(self, A, B, x0): super(TestODEF, self).__init__() self.A = nn.Linear(2, 2, bias=False) self.A.weight = nn.Parameter(A) self.B = nn.Linear(2, 2, bias=False) self.B.weight = nn.Parameter(B) self.x0 = nn.Parameter(x0) def forward(self, x, t): xTx0 = torch.sum(x*self.x0, dim=1) dxdt = torch.sigmoid(xTx0) * self.A(x - self.x0) + torch.sigmoid(-xTx0) * self.B(x + self.x0) return dxdt
एक पूरी तरह से जुड़े नेटवर्क के रूप में गतिशीलता सीखना
class NNODEF(ODEF): def __init__(self, in_dim, hid_dim, time_invariant=False): super(NNODEF, self).__init__() self.time_invariant = time_invariant if time_invariant: self.lin1 = nn.Linear(in_dim, hid_dim) else: self.lin1 = nn.Linear(in_dim+1, hid_dim) self.lin2 = nn.Linear(hid_dim, hid_dim) self.lin3 = nn.Linear(hid_dim, in_dim) self.elu = nn.ELU(inplace=True) def forward(self, x, t): if not self.time_invariant: x = torch.cat((x, t), dim=-1) h = self.elu(self.lin1(x)) h = self.elu(self.lin2(h)) out = self.lin3(h) return out def to_np(x): return x.detach().cpu().numpy() def plot_trajectories(obs=None, times=None, trajs=None, save=None, figsize=(16, 8)): plt.figure(figsize=figsize) if obs is not None: if times is None: times = [None] * len(obs) for o, t in zip(obs, times): o, t = to_np(o), to_np(t) for b_i in range(o.shape[1]): plt.scatter(o[:, b_i, 0], o[:, b_i, 1], c=t[:, b_i, 0], cmap=cm.plasma) if trajs is not None: for z in trajs: z = to_np(z) plt.plot(z[:, 0, 0], z[:, 0, 1], lw=1.5) if save is not None: plt.savefig(save) plt.show() def conduct_experiment(ode_true, ode_trained, n_steps, name, plot_freq=10):
जैसा कि आप देख सकते हैं,
तंत्रिका ODE गतिशीलता को बहाल करने का एक बहुत अच्छा काम करता है। यही है, अवधारणा एक पूरे काम करता है।
अब थोड़ी और जटिल समस्या (MNIST, haha) पर जाँच करें।
तंत्रिका ODE ResNets से प्रेरित है
ResNet'ax में, सूत्र के अनुसार छिपी हुई स्थिति बदल जाती है
जहाँ

ब्लॉक नंबर है और

यह एक फ़ंक्शन है जिसे ब्लॉक के अंदर की परतों द्वारा सीखा जाता है।
सीमा में, यदि हम कभी छोटे कदमों के साथ अनंत संख्या में ब्लॉक लेते हैं, तो हमें ओडीई के रूप में छिपी हुई परत की निरंतर गतिशीलता मिलती है, ठीक उसी तरह जैसा कि ऊपर था।
इनपुट लेयर से शुरू

हम आउटपुट लेयर को परिभाषित कर सकते हैं

समय पर इस ODE के समाधान के रूप में टी।
अब हम गिन सकते हैं

सभी infinitesimal ब्लॉकों के बीच वितरित (
साझा ) मापदंडों के रूप में।
MNIST पर तंत्रिका ODE वास्तुकला को मान्य करना
इस भाग में, हम
तंत्रिका ODE की क्षमता का परीक्षण अधिक परिचित वास्तुशिल्प में घटकों के रूप में करेंगे।
विशेष रूप से, हम MNIST क्लासिफायर में
न्यूरल ODE के साथ अवशिष्ट ब्लॉकों को प्रतिस्थापित करेंगे।
कोड def norm(dim): return nn.BatchNorm2d(dim) def conv3x3(in_feats, out_feats, stride=1): return nn.Conv2d(in_feats, out_feats, kernel_size=3, stride=stride, padding=1, bias=False) def add_time(in_tensor, t): bs, c, w, h = in_tensor.shape return torch.cat((in_tensor, t.expand(bs, 1, w, h)), dim=1) class ConvODEF(ODEF): def __init__(self, dim): super(ConvODEF, self).__init__() self.conv1 = conv3x3(dim + 1, dim) self.norm1 = norm(dim) self.conv2 = conv3x3(dim + 1, dim) self.norm2 = norm(dim) def forward(self, x, t): xt = add_time(x, t) h = self.norm1(torch.relu(self.conv1(xt))) ht = add_time(h, t) dxdt = self.norm2(torch.relu(self.conv2(ht))) return dxdt class ContinuousNeuralMNISTClassifier(nn.Module): def __init__(self, ode): super(ContinuousNeuralMNISTClassifier, self).__init__() self.downsampling = nn.Sequential( nn.Conv2d(1, 64, 3, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), norm(64), nn.ReLU(inplace=True), nn.Conv2d(64, 64, 4, 2, 1), ) self.feature = ode self.norm = norm(64) self.avg_pool = nn.AdaptiveAvgPool2d((1, 1)) self.fc = nn.Linear(64, 10) def forward(self, x): x = self.downsampling(x) x = self.feature(x) x = self.norm(x) x = self.avg_pool(x) shape = torch.prod(torch.tensor(x.shape[1:])).item() x = x.view(-1, shape) out = self.fc(x) return out func = ConvODEF(64) ode = NeuralODE(func) model = ContinuousNeuralMNISTClassifier(ode) if use_cuda: model = model.cuda() import torchvision img_std = 0.3081 img_mean = 0.1307 batch_size = 32 train_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=True, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=batch_size, shuffle=True ) test_loader = torch.utils.data.DataLoader( torchvision.datasets.MNIST("data/mnist", train=False, download=True, transform=torchvision.transforms.Compose([ torchvision.transforms.ToTensor(), torchvision.transforms.Normalize((img_mean,), (img_std,)) ]) ), batch_size=128, shuffle=True ) optimizer = torch.optim.Adam(model.parameters()) def train(epoch): num_items = 0 train_losses = [] model.train() criterion = nn.CrossEntropyLoss() print(f"Training Epoch {epoch}...") for batch_idx, (data, target) in tqdm(enumerate(train_loader), total=len(train_loader)): if use_cuda: data = data.cuda() target = target.cuda() optimizer.zero_grad() output = model(data) loss = criterion(output, target) loss.backward() optimizer.step() train_losses += [loss.item()] num_items += data.shape[0] print('Train loss: {:.5f}'.format(np.mean(train_losses))) return train_losses def test(): accuracy = 0.0 num_items = 0 model.eval() criterion = nn.CrossEntropyLoss() print(f"Testing...") with torch.no_grad(): for batch_idx, (data, target) in tqdm(enumerate(test_loader), total=len(test_loader)): if use_cuda: data = data.cuda() target = target.cuda() output = model(data) accuracy += torch.sum(torch.argmax(output, dim=1) == target).item() num_items += data.shape[0] accuracy = accuracy * 100 / num_items print("Test Accuracy: {:.3f}%".format(accuracy)) n_epochs = 5 test() train_losses = [] for epoch in range(1, n_epochs + 1): train_losses += train(epoch) test() import pandas as pd plt.figure(figsize=(9, 5)) history = pd.DataFrame({"loss": train_losses}) history["cum_data"] = history.index * batch_size history["smooth_loss"] = history.loss.ewm(halflife=10).mean() history.plot(x="cum_data", y="smooth_loss", figsize=(12, 5), title="train error")
Testing... 100% 79/79 [00:01<00:00, 45.69it/s] Test Accuracy: 9.740% Training Epoch 1... 100% 1875/1875 [01:15<00:00, 24.69it/s] Train loss: 0.20137 Testing... 100% 79/79 [00:01<00:00, 46.64it/s] Test Accuracy: 98.680% Training Epoch 2... 100% 1875/1875 [01:17<00:00, 24.32it/s] Train loss: 0.05059 Testing... 100% 79/79 [00:01<00:00, 46.11it/s] Test Accuracy: 97.760% Training Epoch 3... 100% 1875/1875 [01:16<00:00, 24.63it/s] Train loss: 0.03808 Testing... 100% 79/79 [00:01<00:00, 45.65it/s] Test Accuracy: 99.000% Training Epoch 4... 100% 1875/1875 [01:17<00:00, 24.28it/s] Train loss: 0.02894 Testing... 100% 79/79 [00:01<00:00, 45.42it/s] Test Accuracy: 99.130% Training Epoch 5... 100% 1875/1875 [01:16<00:00, 24.67it/s] Train loss: 0.02424 Testing... 100% 79/79 [00:01<00:00, 45.89it/s] Test Accuracy: 99.170%
केवल 5 युगों और 6 मिनट के प्रशिक्षण के दौरान बहुत कठिन प्रशिक्षण के बाद, मॉडल पहले ही 1% से कम की परीक्षण त्रुटि तक पहुंच गया है। हम कह सकते हैं कि
तंत्रिका ODEs एक घटक के
रूप में अधिक पारंपरिक नेटवर्क में एकीकृत होते हैं।
अपने लेख में, लेखक इस क्लासिफ़ायर (ODE-Net) की तुलना एक नियमित रूप से पूरी तरह से जुड़े नेटवर्क के साथ, एक समान आर्किटेक्चर के साथ ResNet के साथ, और ठीक उसी वास्तुकला के साथ करते हैं, जिसमें ढाल सीधे
ODESolve (संयुग्म ढाल विधि के बिना) में संचालन के माध्यम से प्रचारित करता है ( आर-नेट)।
मूल लेख से चित्रण।उनके अनुसार, एक 1-लेयर पूरी तरह से कनेक्टेड नेटवर्क के साथ लगभग समान मापदंडों की संख्या के रूप में
न्यूरल ODE में परीक्षण पर एक बहुत अधिक त्रुटि है, एक ही त्रुटि वाले ResNet में बहुत अधिक पैरामीटर हैं, और RK- नेट बिना संयुग्म ग्रेडिंग विधि के थोड़ी अधिक त्रुटि है। और एक रैखिक रूप से बढ़ती हुई मेमोरी की खपत के साथ (अनुमेय त्रुटि
जितनी छोटी हो,
उतने अधिक कदम
ODESolve होने चाहिए, जो रैखिक रूप से चरणों की संख्या के साथ मेमोरी की खपत को बढ़ाते हैं)।
लेखक यहां सरल इलर विधि के विपरीत, उनके कार्यान्वयन में अनुकूली आकार के साथ निहित रन-कुट्टा विधि का उपयोग करते हैं। वे नई वास्तुकला के कुछ गुणों का भी अध्ययन करते हैं।
ODE- नेट फ़ीचर (NFE फॉरवर्ड - प्रत्यक्ष पास में फ़ंक्शन की संख्या)
मूल लेख से चित्रण।- (ए) संख्यात्मक त्रुटि के स्वीकार्य स्तर को बदलने से प्रत्यक्ष वितरण में चरणों की संख्या में परिवर्तन होता है।
- (b) प्रत्यक्ष वितरण पर खर्च किया गया समय फ़ंक्शन की गणना की संख्या के लिए आनुपातिक है।
- (c) वापस प्रसार के लिए कार्य की गणना की संख्या प्रत्यक्ष प्रसार का लगभग आधा है, जो इंगित करता है कि संयुग्म ग्रेडिएंट विधि सीधे ODESolve के माध्यम से ग्रेडिएंट को फैलाने की तुलना में अधिक कम्प्यूटेशनल रूप से कुशल हो सकती है।
- (घ) ओडीई-नेट अधिक से अधिक प्रशिक्षित हो जाता है, इसके लिए फ़ंक्शन की अधिक से अधिक गणना (एक कभी छोटा कदम) की आवश्यकता होती है, संभवतः मॉडल की बढ़ती जटिलता के लिए अनुकूल।
टाइम सीरीज़ मॉडलिंग के लिए हिडन जनरेटिव फंक्शन
तंत्रिका ODE पथ के अज्ञात स्थान पर होने पर भी निरंतर धारावाहिक डेटा को संसाधित करने के लिए उपयुक्त है।
इस अनुभाग में, हम प्रयोग करेंगे
और तंत्रिका ODE का उपयोग करके निरंतर अनुक्रम की पीढ़ी को बदल देंगे, और सीखे गए छिपे हुए स्थान पर एक नज़र डालेंगे।
लेखक इसकी तुलना आवर्तक नेटवर्क द्वारा उत्पन्न समान अनुक्रमों से भी करते हैं।
यहाँ प्रयोग लेखक के भंडार में संबंधित उदाहरण से थोड़ा अलग है, यहाँ पथों का अधिक विविध सेट है।
डेटा
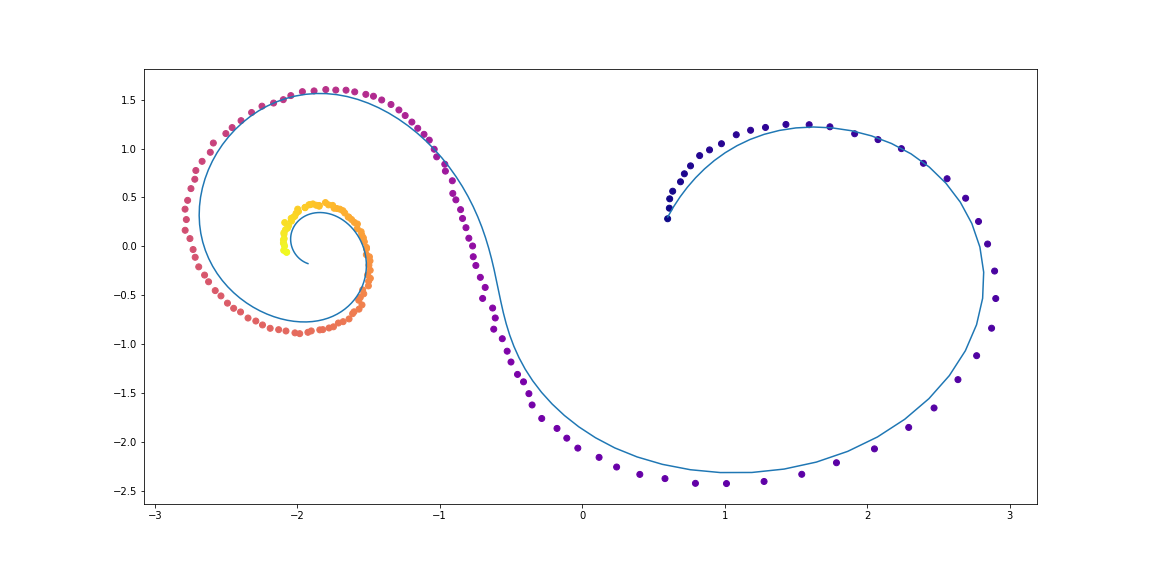
प्रशिक्षण डेटा में यादृच्छिक सर्पिल होते हैं, जिनमें से आधे दक्षिणावर्त होते हैं, और दूसरा वामावर्त। इसके अलावा, इन सर्पिलों से यादृच्छिक क्रमों का नमूना लिया जाता है, जो विपरीत दिशा में कोडिंग पुनरावृत्ति मॉडल द्वारा संसाधित होते हैं, जिससे एक प्रारंभिक छिपे हुए राज्य को जन्म दिया जाता है, जो तब विकसित होता है, छिपी हुई जगह में प्रक्षेपवक्र बनाता है। इस अव्यक्त पथ को तब डेटा स्थान पर मैप किया जाता है और तुलना किए गए परिणाम के साथ तुलना की जाती है। इस प्रकार, मॉडल एक डाटासेट के समान प्रक्षेपवक्र उत्पन्न करने के लिए सीखता है।
डेटासेट सर्पिल के उदाहरणएक जेनेरिक मॉडल के रूप में वीएई
नमूना प्रक्रिया के माध्यम से जनरेटिव मॉडल:
जिसे वैरिएबल ऑटो-एनकोडर दृष्टिकोण का उपयोग करके प्रशिक्षित किया जा सकता है।
- मापदंडों को प्राप्त करने के लिए समय में वापस समय अनुक्रम के माध्यम से एक आवर्तक एनकोडर के माध्यम से जाओ
 ।
।  परिवर्तनशील पश्च वितरण, और फिर उससे नमूना:
परिवर्तनशील पश्च वितरण, और फिर उससे नमूना:
- छिपे हुए प्रक्षेपवक्र प्राप्त करें:
- किसी अन्य तंत्रिका नेटवर्क का उपयोग कर डेटा में एक पथ के लिए एक छिपे हुए मार्ग को मैप करें:

- सैंपल किए गए पथ के लिए वैधता की निचली सीमा (ELBO) के आकलन को अधिकतम करें:
और गॉसियन के बाद के वितरण के मामले में

और ज्ञात शोर स्तर

:
एक छिपे हुए ODE मॉडल के अभिकलन ग्राफ को निम्नानुसार दर्शाया जा सकता है
मूल लेख से चित्रण।इस मॉडल को तब परीक्षण किया जा सकता है कि यह केवल प्रारंभिक टिप्पणियों का उपयोग करके पथ को कैसे प्रक्षेपित करता है।
कोडमॉडल परिभाषित करें
class RNNEncoder(nn.Module): def __init__(self, input_dim, hidden_dim, latent_dim): super(RNNEncoder, self).__init__() self.input_dim = input_dim self.hidden_dim = hidden_dim self.latent_dim = latent_dim self.rnn = nn.GRU(input_dim+1, hidden_dim) self.hid2lat = nn.Linear(hidden_dim, 2*latent_dim) def forward(self, x, t):
डेटसेट जनरेशन
t_max = 6.29*5 n_points = 200 noise_std = 0.02 num_spirals = 1000 index_np = np.arange(0, n_points, 1, dtype=np.int) index_np = np.hstack([index_np[:, None]]) times_np = np.linspace(0, t_max, num=n_points) times_np = np.hstack([times_np[:, None]] * num_spirals) times = torch.from_numpy(times_np[:, :, None]).to(torch.float32)
ट्रेनिंग
vae = ODEVAE(2, 64, 6) vae = vae.cuda() if use_cuda: vae = vae.cuda() optim = torch.optim.Adam(vae.parameters(), betas=(0.9, 0.999), lr=0.001) preload = False n_epochs = 20000 batch_size = 100 plot_traj_idx = 1 plot_traj = orig_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_obs = samp_trajs[:, plot_traj_idx:plot_traj_idx+1] plot_ts = samp_ts[:, plot_traj_idx:plot_traj_idx+1] if use_cuda: plot_traj = plot_traj.cuda() plot_obs = plot_obs.cuda() plot_ts = plot_ts.cuda() if preload: vae.load_state_dict(torch.load("models/vae_spirals.sd")) for epoch_idx in range(n_epochs): losses = [] train_iter = gen_batch(batch_size) for x, t in train_iter: optim.zero_grad() if use_cuda: x, t = x.cuda(), t.cuda() max_len = np.random.choice([30, 50, 100]) permutation = np.random.permutation(t.shape[0]) np.random.shuffle(permutation) permutation = np.sort(permutation[:max_len]) x, t = x[permutation], t[permutation] x_p, z, z_mean, z_log_var = vae(x, t) z_var = torch.exp(z_log_var) kl_loss = -0.5 * torch.sum(1 + z_log_var - z_mean**2 - z_var, -1) loss = 0.5 * ((x-x_p)**2).sum(-1).sum(0) / noise_std**2 + kl_loss loss = torch.mean(loss) loss /= max_len loss.backward() optim.step() losses.append(loss.item()) print(f"Epoch {epoch_idx}") frm, to, to_seed = 0, 200, 50 seed_trajs = samp_trajs[frm:to_seed] ts = samp_ts[frm:to] if use_cuda: seed_trajs = seed_trajs.cuda() ts = ts.cuda() samp_trajs_p = to_np(vae.generate_with_seed(seed_trajs, ts)) fig, axes = plt.subplots(nrows=3, ncols=3, figsize=(15, 9)) axes = axes.flatten() for i, ax in enumerate(axes): ax.scatter(to_np(seed_trajs[:, i, 0]), to_np(seed_trajs[:, i, 1]), c=to_np(ts[frm:to_seed, i, 0]), cmap=cm.plasma) ax.plot(to_np(orig_trajs[frm:to, i, 0]), to_np(orig_trajs[frm:to, i, 1])) ax.plot(samp_trajs_p[:, i, 0], samp_trajs_p[:, i, 1]) plt.show() print(np.mean(losses), np.median(losses)) clear_output(wait=True) spiral_0_idx = 3 spiral_1_idx = 6 homotopy_p = Tensor(np.linspace(0., 1., 10)[:, None]) vae = vae if use_cuda: homotopy_p = homotopy_p.cuda() vae = vae.cuda() spiral_0 = orig_trajs[:, spiral_0_idx:spiral_0_idx+1, :] spiral_1 = orig_trajs[:, spiral_1_idx:spiral_1_idx+1, :] ts_0 = samp_ts[:, spiral_0_idx:spiral_0_idx+1, :] ts_1 = samp_ts[:, spiral_1_idx:spiral_1_idx+1, :] if use_cuda: spiral_0, ts_0 = spiral_0.cuda(), ts_0.cuda() spiral_1, ts_1 = spiral_1.cuda(), ts_1.cuda() z_cw, _ = vae.encoder(spiral_0, ts_0) z_cc, _ = vae.encoder(spiral_1, ts_1) homotopy_z = z_cw * (1 - homotopy_p) + z_cc * homotopy_p t = torch.from_numpy(np.linspace(0, 6*np.pi, 200)) t = t[:, None].expand(200, 10)[:, :, None].cuda() t = t.cuda() if use_cuda else t hom_gen_trajs = vae.decoder(homotopy_z, t) fig, axes = plt.subplots(nrows=2, ncols=5, figsize=(15, 5)) axes = axes.flatten() for i, ax in enumerate(axes): ax.plot(to_np(hom_gen_trajs[:, i, 0]), to_np(hom_gen_trajs[:, i, 1])) plt.show() torch.save(vae.state_dict(), "models/vae_spirals.sd")
एक रात प्रशिक्षण के बाद ऐसा ही होता हैअंक मूल प्रक्षेपवक्र (नीला) के शोर अवलोकन हैं,
पीले इनपुट के रूप में बिंदुओं का उपयोग करते हुए, पुनर्निर्मित और प्रक्षेपित प्रक्षेपवक्र हैं।
डॉट का रंग समय दिखाता है।कुछ उदाहरणों के पुनर्निर्माण बहुत अच्छे नहीं लगते हैं। हो सकता है कि मॉडल पर्याप्त जटिल नहीं है या लंबे समय तक अध्ययन नहीं किया गया है। किसी भी मामले में, पुनर्निर्माण बहुत ही उचित दिखता है।अब देखते हैं कि अगर हम एक क्लॉकवाइज प्रक्षेपवक्र में एक छिपे हुए चर को एक एंटी-क्लॉकवाइज प्रक्षेपवक्र में प्रक्षेपित करते हैं, तो क्या होता है।लेखक न्यूरल ODE और एक सरल पुनरावर्ती नेटवर्क के बीच पुनर्निर्माण और पथ प्रक्षेप की तुलना भी करते हैं ।मूल लेख से चित्रण।लगातार सामान्य होने वाली धाराएँ
. , , (, ), .
, , .
,
.
, ,
, , , .
:
( ) ( ) ;
-X «» ( ) «» ( ).
bekemax .
Neural ODEs . !