स्कूल की पाठ्यपुस्तक II से कार्य

भाग I
भाग II
भाग III

यह आलेख स्वीकृत मानों की श्रेणी और मॉड्यूल युक्त कार्यों के साथ इस पद्धति के संबंध के आकलन की विधि पर चर्चा करता है।

कुछ समस्याओं को हल करते समय, उस सीमा पर विचार करना आवश्यक है जिसके भीतर वांछित मूल्य हो सकता है।

असमानताओं को हल करने के लिए अनुमान विधि पर विचार करें।

मान लीजिए कि माल की प्रति यूनिट कीमत 5 से 10 आरयूबी तक हो सकती है। एक ऊपरी बाध्य देने का मतलब अधिकतम मूल्य निर्धारित करना है जो वांछित मात्रा ले सकता है। माल की दो इकाइयों के लिए, जिसकी कीमत 10 से अधिक नहीं है , ऊपरी अनुमान 10 + 10 = 20 होगा ।

समस्या प्रोफ़ाइल प्रोफ़ाइल एमआई से समस्या पर विचार करें Bashmakova
37. चर के लिए ज्ञात अनुमान $$$x$ और$$ $ इनलाइन $ y: 0 <x <5, 2 <y <3। $ इनलाइन $

निम्नलिखित अभिव्यक्तियों के लिए शीर्ष अंक दें:
1। $$$2x + 3y$
2। $$$xy$

5। $$$\ frac {1} {y}$
6। $$$\ frac {x} {y}$

8। $$$x-y$
9। $$$3x-2y$


सामान्य तौर पर, असीम मात्रा का विश्लेषण एक मूल्यांकन मानदंड का उपयोग करता है। एक मॉड्यूल (एक पड़ोस के रूप में) एक सीमा की परिभाषा में आवेदन पाता है।

$$$ $ प्रदर्शन $ $ \ बायां | x_ {n} -a \ right | <\ varepsilon $$ प्रदर्शन $ $

"अंतर के पाठ्यक्रम और अभिन्न कलन" से उदाहरण पर विचार करें 363 (6)

पंक्ति विचलन सेट करना आसान है

$$

$$\ sum \ frac {1} {\ sqrt {n}} = 1+ \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}} + ...$$

वास्तव में, चूंकि इसके सदस्य घटते हैं, nth आंशिक राशि

$$$ $ $ $ $ 1 + \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}> n \ cdot \ frac {1} {\ sqrt {n }} = \ sqrt {n} $ $ प्रदर्शन $ $

और विज्ञापन के साथ बढ़ता है $$$एन$ ।

ताकि साबित हो सके $$$1+ \ frac {1} {\ sqrt {2}} + ... + \ frac {1} {\ sqrt {n}}$ वास्तव में अधिक है $$$\ sqrt {n}$ , आपको इस अभिव्यक्ति का कम अनुमान लगाने की आवश्यकता है। हम असमानताओं की प्रणाली प्राप्त करते हैं

$$$ $ $ $ $ \ बायाँ {{\ _! शुरू करें {संरेखित} & \ frac {1} {\ sqrt {n-1}}> \ frac {1} {\ sqrt {n}} \\ & \ frac { 1} {\ sqrt {n-2}}> \ frac {1} {\ sqrt {n}} \\ & \ frac {1} {\ sqrt {n-3}}> \ frac {1} {\ sqrt {n}} \\ & ... \ end {संरेखित} \ सही। $ $ प्रदर्शन $ $

इस प्रणाली की सभी असमानताओं को जोड़ने के बाद, हम प्राप्त करते हैं

$$$ $ $ $ $ 1 + \ frac {1} {\ sqrt {2}} + \ frac {1} {\ sqrt {3}} + ... + \ frac {1} {\ sqrt {n}}> \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + \ frac {1} {\ sqrt {n}} + ... + \ frac {1} {\ _ sqrt {n}} = n \ cdot \ frac {1} {\ sqrt {n}} $ $ प्रदर्शन $ $

यह प्रमाण है कि यह श्रृंखला विचलन करती है।

एक हार्मोनिक श्रृंखला के लिए, यह विधि काम नहीं करती है, क्योंकि $$$एन$ आंशिक आंशिक हार्मोनिक श्रृंखला

$$$ $ $ $ $ 1 + \ frac {1} {2} + \ frac {1} {3} + ... + \ frac {1} {n}> n \ cdot \ frac {1} {n} = 1 $ $ प्रदर्शन $ $

वापस कार्य के लिए

38. राशि की गणना करें ("5 से 15 वर्ष के बच्चों के लिए कार्य")

$$

$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ _ cdot3} + \ frac {1} {3 \ cdot4} + ... + \ frac {1} {99 \ _ cdot100}$$

(उत्तर के 1% से अधिक की त्रुटि के साथ)

श्रृंखला का शीर्ष अनुमान $$$\ frac {n} {n + 1}$ नंबर 1 देता है।

पहला पद छोड़ो $$$\ frac {1} {1 \ cdot2}$

(define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 1.0 )(+ n 2.0))) (series_sum_1(- n 1.0))) ) ) ) (writeln (series_sum_1 10)) (writeln (series_sum_1 100)) (writeln (series_sum_1 1000)) (writeln (series_sum_1 10000)) (writeln (series_sum_1 100000)) (writeln (series_sum_1 1000000)) 

हमें मिलता है $$$1 - \ frac {1} {1 \ cdot2} = \ frac {1} {2}$
.41666666666666663
.49019607843137253
0.4990019960079833
0.4999000199960005
.49999000019998724
0.4999990000019941

आप ideone.com में यहाँ देख सकते हैं


पहले दो पद छोड़ें $$$\ frac {1} {1 \ cdot2} + \ frac {1} {2 \ cdot3}$

 (define series_sum_1 ( lambda (n) (if (= n 0) 0 (+ (/ 1.0 (* (+ n 2.0) (+ n 3.0))) (series_sum_1(- n 1.0))) ) ) ) (series_sum_1 1000000) 

हमें 0.33333233333632745 मिलेगा
श्रृंखला के आंशिक योग ऊपर दिए गए हैं।

सकारात्मक पंक्ति में हमेशा एक राशि होती है; यह राशि परिमित होगी (और इसलिए श्रृंखला अभिसरण) यदि श्रृंखला के आंशिक योग ऊपर बंधे हैं, और अनंत (और श्रृंखला विचलन) अन्यथा।

दूर फेंक दो $$$एन$ हार्मोनिक श्रृंखला के प्रारंभिक शब्द।
साबित करें (निचले बाउंड का उपयोग करके) कि

$$$ $ $ $ $ $ $ + 1 = {n + 1} + \ frac {1} {n + 2} + ... + \ frac {1} {2n}> \ frac {1} {2} $ $ $ $ प्रदर्शित करें

यदि, पहले दो शब्दों को छोड़ दें, तो हार्मोनिक श्रृंखला के शेष सदस्यों को समूहों में विभाजित किया गया है $$$2,4,8, ..., 2 ^ {k-1}, ...$ प्रत्येक में सदस्य

$$

$$\ frac {1} {3} + \ frac {1} {4}; \ frac {1} {5} + \ frac {1} {6} + \ frac {1} {7} + \ frac {1} {8}; \ frac {1} {9} + ... \ frac {1} {16}; ...;$$

$$

$$\ frac {1} {2 ^ {k-1} +1} + ... + \ frac {1} {2 ^ {2}}; ...,$$

फिर इनमें से प्रत्येक राशि व्यक्तिगत रूप से बड़ी होगी $$$\ frac {1} {2}$ ।
... हम देखते हैं कि आंशिक रकम ऊपर नहीं बांधी जा सकती है: श्रृंखला में एक अनंत राशि है।

हम आंशिक मात्रा की गणना करते हैं जो त्यागने से प्राप्त होती हैं $$$2 ^ {के}$ शर्तों।

 #lang racket (* 1.0 (+ 1/3 1/4)) (* 1.0 (+ 1/5 1/6 1/7 1/8)) (* 1.0 (+ 1/9 1/10 1/11 1/12 1/13 1/14 1/15 1/16)) 

हमें मिलता है:
0.5833333333333334
0.6345238095238095
0.6628718503718504
हम एक प्रोग्राम लिखते हैं जो हार्मोनिक श्रृंखला के योग की गणना करता है $$$\ frac {n} {2}$ को $$$एन$ जहाँ $$$n = 2 ^ {k}$ पर $$$k \ in \ mathbb {N}$

 #lang racket (define (Hn n ) (define half_arg (/ n 2.0)) (define (series_sum n) (if (= n half_arg ) 0 (+ (/ 1.0 n) (series_sum(- n 1)) ) ) ) (series_sum n) ) (Hn 4) (Hn 8) (Hn 16) (Hn 32) 

हमें मिलता है:
0.5833333333333333
0.6345238095238095
0.6628718503718504
0.6777662022075267

आप लिंक पर ऑनलाइन विचारधारा में देख सकते हैं
सीमा के लिए $$$\ छोड़ दिया [1 + 2 ^ {70}; 2 ^ {71} \ सही]$ हमें 0.693147 मिलता है ...
यहां वुल्फराम क्लाउड में मोजो की जांच करें ।

यह पुनरावर्ती एल्गोरिथ्म एक तेज स्टैक अतिप्रवाह का कारण बनता है।
इस लेख में एक पुनरावृत्त एल्गोरिथ्म का उपयोग करके फैक्टरियल की गणना करने का एक उदाहरण है। हम इस पुनरावृत्त एल्गोरिथ्म को संशोधित करते हैं ताकि यह कुछ सीमाओं के भीतर आंशिक योग Hn की गणना करे; इन सीमाओं को बुलाओ और बी

 (define (Hn ab) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a)) 

निचली सीमा संख्या है $$$1 + 2 ^ {k}$ , ऊपरी बाउंड संख्या है $$$2 \ cdot 2 ^ {k}$
हम एक फ़ंक्शन लिखते हैं जो दो की शक्ति की गणना करता है

 (define (power_of_two k) (define (iteration product counter) (if (> counter k) product (iteration (* product 2) (+ counter 1)))) (iteration 1 1)) 

हम निचली सीमा के रूप में (+ 1 (power_of_two k)) स्थानापन्न करेंगे, और ऊपरी सीमा के रूप में फ़ंक्शन (* 2 (power_of_two k)) या इसके समकक्ष कार्य (power_of_two (+ 1 k)) का उपयोग करेंगे।
फ़ंक्शन एचएन को फिर से लिखें

 (define (Hn k) (define a (+ 1 (power_of_two k)) ) (define b (* 2 (power_of_two k)) ) (define (iteration product counter) (if (> counter b) product (iteration (+ product (/ 1.0 counter)) (+ counter 1)))) (iteration 0 a )) 

अब आप बड़े मानों के लिए Hn की गणना कर सकते हैं $$$k$ ।

हम सी में एक प्रोग्राम लिखते हैं जो एचएन की गणना के लिए आवश्यक समय को मापता है। हम <time.h> मानक पुस्तकालय से घड़ी () फ़ंक्शन का उपयोग करेंगे
प्रोसेसर का समय मापने के बारे में एक लेख यहां हैबे पर है ।

 #include <math.h> #include <stdio.h> #include <time.h> int main(int argc, char **argv) { double count; // k  1+2^30  2^31 for(unsigned long long int i=1073741825 ;i<=2147483648 ;i++) { count=count+1.0/i; } printf("Hn = %.12f ", count); double seconds = clock() / (double) CLOCKS_PER_SEC; printf("  %f  \n", seconds); return 0; } 

आमतौर पर ऑनलाइन ide प्रोग्राम को चलाने का निष्पादन समय पाँच सेकंड तक सीमित करता है, इसलिए इस प्रोग्राम को केवल कुछ ऑनलाइन ide में चेक किया जा सकता है, उदाहरण के लिए, onlinegdb.com या repl.it।
K से 1 + 2 ^ 30 से 2 ^ 31 तक, ऑपरेटिंग समय ~ 5 सेकंड होगा।
K से 1 + 2 ^ 31 से 2 ^ 32 के लिए, ऑपरेटिंग समय ~ 10 सेकंड होगा।
K से 1 + 2 ^ 32 से 2 ^ 33 के लिए, ऑपरेटिंग समय ~ 20 सेकंड होगा।
K से 1 + 2 ^ 33 से 2 ^ 34 तक, ऑपरेटिंग समय ~ 40 सेकंड होगा।
K से 1 + 2 ^ 34 से 2 ^ 35 तक, ऑपरेटिंग समय एक मिनट से अधिक होगा।
...
K से 1 + 2 ^ 45 से 2 ^ 46 तक, परिचालन समय 24 घंटे से अधिक होगा।

मान लीजिए कि k से 1 + 2 ^ 30 से 2 ^ 31 तक, एल्गोरिथम का निष्पादन समय ~ 2 सेकंड है।
फिर k = 2 ^ (30 + n) के लिए एल्गोरिथ्म का निष्पादन समय 2 ^ n सेकंड है। (कम से $$$n \ in \ mathbb {N}$ )
इस एल्गोरिथ्म में घातीय जटिलता है ।

वापस मॉड्यूल के लिए।
अभिन्न कलन में, सूत्र में मॉड्यूल का उपयोग किया जाता है

$$

$$\ int \ frac {1} {x} dx = \ int \ frac {dx} {x} = ln \ left | x \ सही | + क$$

Habré पर एक लेख था सबसे प्राकृतिक लघुगणक जिसमें यह अभिन्न माना जाता है और इसकी संख्या की गणना के आधार पर $$$ई$ ।

सूत्र में मॉड्यूल की उपस्थिति $$$\ int \ frac {dx} {x} = ln \ left | x \ सही | + क$ "अंतर के अंतर और अभिन्न कलन" में आगे की पुष्टि

यदि ...$$ $ इनलाइन $ x <0 $ इनलाइन $ , तो विभेदन द्वारा यह सत्यापित करना आसान है $$$\ छोड़ दिया [ln (-x) \ right] '= \ frac {1} {x}$

अभिन्न का शारीरिक अनुप्रयोग $$$\ int \ frac {dx} {x}$

इस अभिन्न का उपयोग बेलनाकार संधारित्र की प्लेटों के संभावित अंतर की गणना करने के लिए किया जाता है।


"बिजली और चुंबकत्व":

प्लेटों के बीच संभावित अंतर एकीकरण द्वारा पाया जाता है:

$$

$$\ varphi_ {1} - \ varphi_ {2} = \ int \ limit_ {R_ {1}} ^ {R_ {2}} E (r) dr = \ frac {q} {2 \ _ \ _ \ _ varepsilon_ {0} \ varepsilon l} \ int \ limit_ {R_ {1}} ^ {R_ {2}} \ frac {dr} {r} = \ frac {q} {2 \ pi \ varepsilon_ [0} \ _ varepsilon l} ln \ frac {R_ {2}} {R_ {1}}$$

( $$$R_ {1}$ और $$$R_ {2}$ - आंतरिक और बाहरी प्लेटों की त्रिज्या)।

प्राकृतिक लघुगणक के संकेत के तहत यहां मॉड्यूल चिन्ह का उपयोग नहीं किया जाता है $$$ln \ left | \ frac {R_ {2}} {R_ {1}} \ right |$ क्योंकि $$$R_ {1}$ और $$$R_ {2}$ सख्ती से सकारात्मक और रिकॉर्डिंग का यह रूप बेमानी है।

"मॉड्यूलर" ड्राइंग

मॉड्यूल का उपयोग करके, आप विभिन्न आकृतियों को आकर्षित कर सकते हैं।

यदि जियोजेब्रा प्रोग्राम में सूत्र लिखें $$$abs (x) + abs (y) = 1$ हमें मिलता है



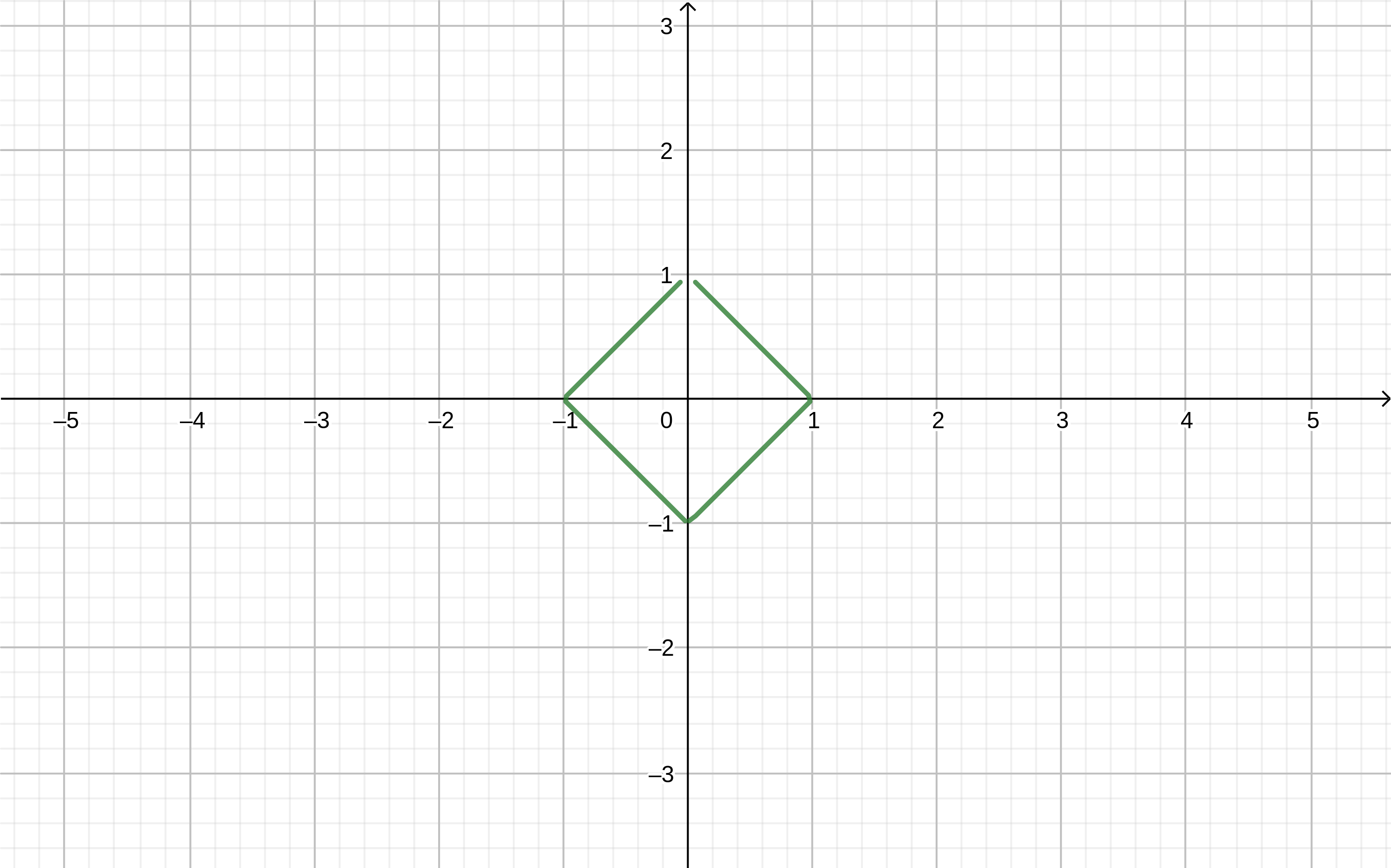
आप अधिक जटिल आकृतियाँ बना सकते हैं। चलो, उदाहरण के लिए, वुल्फरामअल्फा बादल में एक "तितली"

$$

$$\ sum \ frac {\ बाईं ओर | x \ सही | } {n- \ left | x \ सही | } + \ _ frac {\ _ बाएं | x + n \ सही | } {n} + \ _ frac {\ _ left | x-n \ सही | } {n}$$

प्लॉट [Sum [abs (x) / (n-abs (x)) + abs (x + n) / (n) + abs (xn) / (n), {n, 1,20}], {x, -60.60}]
इस अभिव्यक्ति में $$$एन$ से रेंज में है $$$1$ को $$$20$ । $$$x$ से रेंज में है $$$-60$ को $$$60$ ।
तस्वीर का लिंक ।

पुस्तकें:

“प्रोफाइल ओरिएंटेशन की कार्य पुस्तक” एम.आई. जूते
सामान्य भौतिकी पाठ्यक्रम: 3 संस्करणों में टी। 2. "बिजली और चुंबकत्व" आई.वी. Savelyev