क्वांटम रसायन विज्ञान के संदर्भ में मून उत्प्रेरक। भाग I: साधारण हाइड्रोजन बनाम। म्यूऑन हाइड्रोजन

Mnogabukaff कि क्वांटम रसायन विज्ञान मुओन कटैलिसीस के सिद्धांत के बारे में सोचता है: कैसे मुआन वांछित प्लाज्मा के तापमान को कम करता है। दो भागों में।

पहले भाग का सार एक वाक्य में व्यक्त किया गया है: म्यूऑन इलेक्ट्रॉन से भारी है, इसलिए इसे प्रोटॉन से दूर फाड़ना अधिक कठिन है।

लेकिन जो लोग सूत्र, रेखांकन को देखना चाहते हैं, और क्वांटम रसायन विज्ञान के वैचारिक सार को देखते हैं, जैसा कि सरलतम (अर्ध) परमाणुओं पर लागू होता है, बिल्ली के नीचे स्वागत है।

दूसरा भाग इस लिंक पर उपलब्ध है।

परिचय

यह कोई रहस्य नहीं है कि मैनकाइंड द्वारा ऊर्जा की खपत हर साल बढ़ रही है: हम में से प्रत्येक के पास अधिक गैजेट हैं, हमें वहां घूमना है, और हम खुद भी कम नहीं हैं। इसलिए, हम निरंतर विचार में हैं, कहां अधिक ऊर्जा प्राप्त करना है, और इस ऊर्जा को कहां बचाना है।

ऊर्जा के वर्तमान मुख्य स्रोतों (कोयला, गैस, पनबिजली संयंत्रों और परमाणु ऊर्जा) के संभावित विकल्पों में से एक थर्मोन्यूक्लियर फ्यूजन (टीएस) है । वास्तव में, यह दुष्ट परमाणु ऊर्जा का अच्छा जुड़वां भाई है। ज़ार-बम के बारे में याद नहीं रखने वाली मुख्य बात यह है : परमाणु क्षय प्रतिक्रियाओं के बजाय, हल्के नाभिकों का भारी मात्रा में संलयन ऊर्जा स्रोत के रूप में कार्य करता है। और सब कुछ ठीक लगता है: हमारे सभी ऊर्जा स्रोत किसी न किसी तरह टीएस के लिए धन्यवाद प्रकट हुए हैं, क्योंकि यह तारों में (सूर्य के अंदर सहित) बहता है और प्रकाश और गर्मी के स्रोत के रूप में कार्य करता है, जिसके कारण सभी प्रकाश संश्लेषण प्रतिक्रियाएं होती हैं, सभी प्रवाह नदियाँ और हवाएँ चलती हैं। लेकिन टीएस के लिए भी धन्यवाद, हमारे पास हीलियम (कार्बन = कोयला, तेल, गैस, और यूरेनियम) की तुलना में भारी तत्वों का एक गुच्छा है।
मुख्य पुटीय संश्लेषण प्रतिक्रियाएं विभिन्न हाइड्रोजन समस्थानिकों (प्रोटियम) की संलयन प्रतिक्रियाएं हैं $$${} _ {1} ^ {1} \ mathrm {H}$ ड्यूटेरियम $$${} _ {1} ^ {2} \ mathrm {H}$ और ट्रिटियम $$${} _ {1} ^ {3} \ mathrm {H}$ )।

समस्या यह है कि वाहन को आत्मनिर्भर मोड में शुरू करने के लिए आपको अत्यधिक उच्च तापमान की आवश्यकता होती है। तारों के साथ कोई समस्या नहीं है, लेकिन स्थलीय परिस्थितियों में, इस तरह की आवश्यकता अभी भी हर आउटलेट में एक पर्यावरण के अनुकूल थर्मोन्यूक्लियर संलयन से वर्तमान प्रवाह के लिए एक बाधा है।

तापमान कम करने का एक तरीका म्यूऑन कैटेलिसिस है ।
विकी हमें बताता है कि मुऑन ( $$$\ _मु ^ -$ ) क्या ऐसा अस्थिर भारी इलेक्ट्रॉन क्लोन है ( $$$ई ^ -$ ): यह एक इलेक्ट्रॉन से 207 गुना भारी है, और केवल 2.2 माइक्रोसेकंड रहता है। लेकिन, यह माना जाता है कि सिस्टम में ऐसे कणों के अलावा जहां टीएस होता है, नए न्यूक्लियर के संलयन के लिए आवश्यक न्यूनतम प्लाज्मा तापमान को कम करने में सक्षम होगा। और चूंकि कुछ संश्लेषण प्रतिक्रियाओं के दौरान म्यूऑन बन सकते हैं, इसलिए नए कणों को क्षय होने के बजाय दिखाई देना चाहिए, जो हाइड्रोजन और अन्य तत्वों को भारी बनाने के साथ जलाने के लिए कीमिया में संलग्न होने की अनुमति देगा।

हाइड्रोजन के सामान्य रूपों और उन लोगों के बीच के अंतर में जहां इलेक्ट्रॉन को म्यूऑन द्वारा बदल दिया जाता है और म्यूऑन कैटेलिसिस के पूरे सार को कवर किया जाता है। और इसे देखने के लिए, हमें क्वांटम रसायन विज्ञान और इसकी अवधारणाओं की ओर मुड़ना होगा, जो हम करेंगे।

इस भाग में, हम हाइड्रोजन परमाणु में अंतर पर ध्यान देंगे ( $$$\ mathrm {H ^ \ cdot = p ^ + e ^ -}$ ) अपने म्यूऑन समकक्ष ( $$$\ mathrm {p} ^ + \ mu ^ -$ ), जिसमें इलेक्ट्रॉन को म्यूऑन द्वारा प्रतिस्थापित किया जाता है।

प्रोटॉन के घोंसले पर उड़ान ...

आम शब्दों की एक जोड़ी

हाइड्रोजन परमाणु। हर कोई इस पर चर्चा करता है और स्कूल में भौतिकी और रसायन विज्ञान कक्षाओं में जगह लेता है, इसलिए हम चर्चा करेंगे कि एक इलेक्ट्रॉन को म्यूऑन के साथ प्रतिस्थापित करने से इसके गुणों (ऊर्जा और प्रकार की कक्षा) पर क्या प्रभाव पड़ेगा।
हम इन कणों को दो सामान्य स्थितियों से समझते हैं:

• विकृत (तथाकथित पुराने क्वांटम यांत्रिकी),
• और सामान्य क्वांटममेच के दृष्टिकोण से।

पहला विचार स्कूली बच्चों के लिए उपलब्ध है, दूसरे को उच्च गणित के गहन ज्ञान की आवश्यकता होगी।

बोह्र की परिक्रमा

वास्तव में, पुरानी क्वांटम यांत्रिकी शास्त्रीय यांत्रिकी को उन प्रणालियों का वर्णन करने के लिए अनुकूलित करने का एक प्रयास है जो इसे नहीं मानते हैं। इस तथ्य के बावजूद कि पूर्ण विवरण के लिए, यह दृष्टिकोण बहुत त्रुटिपूर्ण है (जिसे हम अगले भाग में चर्चा करेंगे), यह महत्वपूर्ण और दिलचस्प है, और एक ही समय में असामान्य रूप से सरल है।

• सबसे पहले, यह पुराने क्वांटम यांत्रिकी के माध्यम से था जो भौतिकविदों ने सूँघने में कामयाब रहे कि क्वांटम सिस्टम के साथ क्या गलत था, इसलिए, एक ऐतिहासिक दृष्टिकोण से, भौतिकी के प्रतिमान को बदलने के लिए यह कदम आवश्यक और महत्वपूर्ण था।
• दूसरे, बोह्र के हाइड्रोजन के परमाणुओं की समस्या के समाधान में दो कणों से मिलकर सकारात्मक और नकारात्मक चार्ज किए गए हैं जो प्रयोगात्मक अवलोकनों की व्याख्या कर सकते हैं और हाइड्रोजन स्पेक्ट्रा में श्रृंखला के पूरे देखे गए चिड़ियाघर को एक साथ जोड़ सकते हैं। इस निर्णय का एक हानिकारक संस्करण, जिसने बोहर को नोबेल 1922 लाया, हम यहां पर विचार करेंगे।

लेकिन समस्या को हल करने के लिए, हमें यह याद रखना चाहिए कि हम शास्त्रीय मामले में एक कण की गति का वर्णन कैसे करते हैं। यह भौतिकी में एक स्कूल कार्यक्रम है, लेकिन अगर कोई भूल गया, तो आप अपनी याददाश्त को ताज़ा कर सकते हैं:




चलिए कार्य पर चलते हैं। तो, हमारे पास दो विपरीत आवेशित कण होते हैं जो कूलम्ब कानून के अनुसार एक दूसरे की ओर आकर्षित होते हैं, अर्थात्। आकर्षण की संभावित ऊर्जा है

$$

$$V (R) = \ overbrace {\ frac {1} {4 \ pi \ varepsilon_0}} ^ {k} \ frac {q_1 q_2} {R} = k \ frac {q_1_2} {R}$$

जहां R कणों के बीच की दूरी है, $$$q_i$ - हाइड्रोजन परमाणु और एक कण के मामले में शुल्क $$$\ mathrm {p} ^ + \ mu ^ -$ वे बराबर हैं $$$+ e \ लगभग +1.6 बार 10 ^ {- 19}$ प्रोटॉन और के लिए सी.एल. $$$-ई$ इलेक्ट्रॉन और म्यूऑन के लिए, और $\ varepsilon_0$ - विद्युत स्थिरांक । चूंकि आरोप विपरीत हैं, इसलिए संभावित ऊर्जा कणों के बीच की दूरी (यानी, दृष्टिकोण के दौरान) के साथ कम हो जाती है, जिसका अर्थ है कि प्रोटॉन और इलेक्ट्रॉन / म्यूऑन एक दूसरे के प्रति आकर्षित होते हैं।

यह स्थिति ऊपर चित्र में दिखाई गई है। लेकिन कहीं हमने एक समान प्रणाली देखी, है ना? दरअसल, इनमें से एक जोड़े पर हम रहते हैं: सूर्य + पृथ्वी या पृथ्वी + चंद्रमा, या पृथ्वी + आईएसएस - ये भी दो कण हैं जो न्यूटन के नियम द्वारा व्यक्त की गई समान क्षमता से आकर्षित होते हैं:

$$

$$V (R) = -G \ frac {m_1 m_2} {R}$$

जहां जी गुरुत्वाकर्षण स्थिरांक है, और $$$m_i$ - जनता।

प्रोटॉन इलेक्ट्रॉन की तुलना में 1836 गुना भारी है, और चूंकि म्यूऑन इलेक्ट्रॉन से 207 गुना भारी है, प्रोटॉन म्यूऑन की तुलना में लगभग 9 गुना भारी है। दोनों मामलों में, हमारे पास "भारी कण + प्रकाश कण" प्रणाली है, इसलिए हम उस अनुमान को लेते हैं जिसमें इलेक्ट्रॉन / म्यूऑन एक प्रोटॉन के चारों ओर घूमता है। बेशक, के मामले में इस धारणा की सटीकता $$$\ mathrm {p} ^ + \ mu ^ -$ हाइड्रोजन परमाणु की तुलना में काफी कम होगा, लेकिन चित्रण के लिए यह काफी उपयुक्त है। सूर्य + पृथ्वी के मामलों में, पृथ्वी + आईएसएस आमतौर पर समान सन्निकटन का उपयोग करते हैं।

हम एक स्थिर प्रणाली में रुचि रखते हैं जिसमें कुछ भी कहीं भी नहीं गिरता है, क्योंकि हाइड्रोजन परमाणु, यदि अछूता छोड़ दिया जाता है, तो बहुत लंबे समय तक मौजूद रहता है।

हम सौर मंडल से सभी एनालॉग्स के मामले में इस तरह के आंदोलनों को जानते हैं, लेकिन पृथ्वी + आईएसएस जोड़ी के लिए भी स्पष्ट हैं: ये स्थिर परिक्रमाएं हैं, जिस पर स्टेशन पृथ्वी के चारों ओर गति से चलता है, जो गिरने के लिए पर्याप्त नहीं है। इस गति को पहली ब्रह्मांडीय गति कहा जाता है, अर्थात हमें हाइड्रोजन परमाणु / इसके म्यूऑन समकक्ष के लिए पहले ब्रह्मांडीय वेग की आवश्यकता होगी। और इसे स्कूल सूत्रों द्वारा खोजना आसान है (ऊपर दिए गए आंकड़े देखें)।

त्रिज्या आर के साथ एक गोलाकार कक्षा में घूमते समय (चित्र में यह संकेत दिया गया है $$$a_0$ , और जल्द ही हम इसे प्राप्त करते हैं) आपके पास गति होनी चाहिए $$$वी$ । कोई कल्पना कर सकता है कि हर क्षण एक वृत्त में उड़ते हुए कण पर कार्य करने वाली दो सेनाएँ वेग सदिश के लंबवत होती हैं:

• गुरुत्वाकर्षण की कूलम्ब बल केंद्र की ओर निर्देशित होती है, जो बल की परिभाषा के अनुसार होती है $$$F = - \ frac {dV} {dR}$ के बराबर है
  

  $$

  $$F_ \ text {K} = -k \ frac {e ^ 2} {R ^ 2}$$
  
  
• (नकली) केन्द्रापसारक बल इसका प्रतिकार करता है, जो कक्षा R की त्रिज्या को बढ़ाने की कोशिश करता है, इसके लिए अभिव्यक्ति का रूप है
  

  $$

  $$F_ \ text {q} = \ frac {mv ^ 2} {R}$$
  
  जहाँ m इलेक्ट्रॉन / muon (प्रोटॉन का प्राकृतिक उपग्रह) का द्रव्यमान है।
  

यह स्थिति कि एक हल्का कण एक भारी दुर्घटना नहीं करता है, यह है कि इन बलों का योग कण की गति की दिशा के लंबवत है (शून्य) $$$F_ \ mathrm {K} + F_ \ mathrm {q} = 0$ ), जिसका अर्थ है कि हम समीकरण प्राप्त करते हैं

$$

$$\ frac {mv ^ 2} {R} = k \ frac {e ^ 2} {R ^ 2}$$

जहाँ हमें गति मिलती है, जिसके साथ इलेक्ट्रॉन / म्यूऑन को उड़ाना आवश्यक है, जो कि बड़े पैमाने पर m के साथ कक्षा R की त्रिज्या पर होता है, ताकि प्रोटॉन पर दुर्घटना न हो:

$$

$${v} = \ sqrt {k \ frac {e ^ 2} {mR}}$$

और अगर इलेक्ट्रान / म्यूऑन को चार्ज नहीं किया जाता है, तो सब कुछ चोट पहुंचेगा, और चार्ज किए गए कण एक सर्कल में चलते समय विद्युत चुम्बकीय तरंगों का उत्सर्जन करते हैं (इसे उज्ज्वल घर्षण कहा जाता है) , जो इस तरह की प्रणाली को अस्थिर करेगा: इलेक्ट्रॉन / म्यूऑन रोटेशन के दौरान प्रकाश उत्सर्जित करेगा, नतीजतन, इसने ऊर्जा खो दी और इसकी कक्षा की त्रिज्या को कम कर दिया, और अंततः यह एक प्रोटॉन पर गिर जाएगा, और हर चीज के लिए थोड़ा सफेद शराबी जानवर होगा । लेकिन, स्पष्ट रूप से, ऐसा नहीं होता है, जिसका अर्थ है कि इलेक्ट्रॉन / म्यूऑन जैसे छोटे कणों के व्यवहार में कुछ अलग होना चाहिए।

दरअसल, नील्स बोह्र ने उस समय एक बहुत गूंगा (उस समय) परिकल्पना का प्रस्ताव रखा था। उन्होंने स्वीकार किया कि एक निश्चित त्रिज्या के साथ कक्षाएँ हैं, जिन पर हाइड्रोजन परमाणु कुछ भी उत्सर्जित नहीं करता है। और अब सवाल यह है कि इन कक्षाओं को कैसे खोजें। सादगी के लिए, हम बाद में बोहर के लिए उपलब्ध उपलब्धि का उपयोग करेंगे: डी ब्रोगली तरंग दैर्ध्य के लिए अभिव्यक्ति:

$$

$$\ lambda = \ frac {h} {p} = \ frac {h} {mv}$$

यह माना जाता है कि पदार्थ (कणों) में भी तरंग गुण होते हैं, और उन्हें एक निश्चित तरंग दैर्ध्य कहा जा सकता है, जो कि डी ब्रोगली सूत्र द्वारा दिया गया है। फिर, एक सर्कल में गति के लिए समय में स्थिर होने के लिए (एक लहर होने के लिए), यह आवश्यक है कि कक्षा की लंबाई ( $$$L = 2 \ pi R$ ) तरंगों की एक पूर्णांक संख्या फिट।

तब इलेक्ट्रॉन / म्यूऑन की तरंग गति को किसी तरह इस तरह दर्शाया जा सकता है ( विकी से लिया गया ):

सूत्रों की भाषा में, इसे इस रूप में व्यक्त किया गया है:

$$

$$2 \ pi R = n \ lambda = n \ frac {h} {mv}$$

यहां उपर्युक्त पहला कॉस्मिक प्रोटॉन वेग प्राप्त करने से, हम समीकरण प्राप्त करते हैं $$$2 \ pi R = \ frac {nh} {m} \ sqrt {\ frac {mR} {ke ^ 2}}$ । दोनों पक्षों को चुकता करने के बाद, हम nth स्थिर इलेक्ट्रॉन / म्यूऑन कक्षा की त्रिज्या के लिए अभिव्यक्ति प्राप्त करते हैं:

$$

$$R_n = n ^ 2 \ बाएँ (\ overbrace {\ frac {h} {2 \ pi}} ^ {\ hbar} \ right) ^ 2 \ cdot \ frac {1} {mk e ^ 2} \ "frac { n ^ 2 \ hbar ^ 2} {mk e ^ 2}$$

यहां $$$n = 1,2,3, \ ldots$ (हमारे पास रखी जाने वाली तरंगों की संख्या पर सीमा नहीं है), और $$$\ _ हबर$ - यह तथाकथित है प्लैंक स्थिर। जितनी अधिक तरंगें हम ढेर करते हैं, कक्षा की त्रिज्या जितनी बड़ी होती है। इलेक्ट्रॉन के मामले में न्यूनतम त्रिज्या ( n = 1) के साथ (यानी, m , इलेक्ट्रॉन m _e के द्रव्यमान के बराबर है), इस त्रिज्या को बोहर त्रिज्या कहा जाता है, जैसा कि केओ कहते हैं, निओ बोहर के सम्मान में, और इसे _{0 के} रूप में दर्शाया गया है (देखें) अंजीर ऊपर):

$$

$$a_0 = R_0 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} ke ^ 2}$$

संख्याओं का प्रतिस्थापन ( 1.0 = 1.054 × ^10–34 J · s, m _e = 9.109 × 10 ^-31 किग्रा, k = 8.99 × 10 ⁹ N · m ² · C and2 और e = −1.602 × 10 − 19 C) मान ₀ = 5.29 × 10 ^a11 मीटर या 0.529 angstroms (0)।


गणना के दौरान, हमने एक नई इकाई शुरू की है: संख्या $$$n = 1,2,3, \ ldots$ जो तरंगों की संख्या निर्धारित करता है और $$$\ Rightarrow$ कक्षा की त्रिज्या, और कक्षा में इलेक्ट्रॉन की गति भी। यह संख्या स्कूल से सभी के लिए जानी जाती है: यह हाइड्रोजन जैसी परमाणु की सबसे महत्वपूर्ण मात्रा है। हम इसके बारे में अगले खंड में और अधिक विस्तार से बात करेंगे, लेकिन अभी के लिए आप प्रत्येक स्तर की ऊर्जा खोजने की कोशिश कर सकते हैं।

जैसा कि हम इसे समझते हैं, एक बंद प्रणाली की ऊर्जा (और इसमें कोई संदेह नहीं है कि हमारे हाइड्रोजन जैसा परमाणु ऐसा है) दो भागों में शामिल हैं:

• गतिज ऊर्जा से $$$T = \ frac {mv ^ 2} {2}$ ।
• और संभावित है, जो हमारे मामले में कूलम्ब के कानून द्वारा दिया गया है $$$V = \ frac {के ^ 2} {R}$ ।

हम चुने हुए प्रिंसिपल नंबर n के लिए उनमें कक्षा की गति और त्रिज्या का विकल्प देते हैं। हमने पहले ही त्रिज्या लिख ​​दिया है, लेकिन गति जैसी दिखेगी $$$v_n ^ 2 = \ frac {k e ^ 2} {m R_n} = \ frac {k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ ।

तो $$$T_n = \ frac {m v_n ^ 2} {2} = \ frac {m} {2} = \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$ । क्षमता के साथ, सब कुछ सरल है: $$$V_n = - \ frac {ke ^ 2} {R_n} = - \ frac {m k ^ 2 e ^ 4} {n ^ 2 \ hbar ^ 2}$ । इन योगदानों को समेटते हुए, हम हाइड्रोजन जैसी परमाणु की कुल ऊर्जा प्राप्त करते हैं:

$$

$$E_n = T_n + V_n = - \ frac {m k ^ 2 e ^ 4} {2 n ^ 2 \ hbar ^ 2}$$

और इस सूत्र ने क्वांटम यांत्रिकी की शुद्धता को साबित करने में एक बड़ी भूमिका निभाई, क्योंकि वर्णक्रमीय रेखा श्रृंखला (लिमन, बामर, पासचेन, आदि) के ढेर हाइड्रोजन परमाणु के स्पेक्ट्रा में देखे गए थे। और एक सूत्र और एक सरल मॉडल के साथ, वे सभी एक ही बार में समझाए जाने में कामयाब रहे, जो बोहर के विचारों को पहचानने के पक्ष में एक बहुत ही ठोस तर्क था।

इस सरल मॉडल से सभी रसों को निचोड़ने के बाद, हम ईमानदार क्वांटम यांत्रिकी के दृष्टिकोण से समस्या के सही विचार के लिए आगे बढ़ सकते हैं।

हाइड्रोजन जैसे परमाणु के ऑर्बिटल्स

दूसरा, इससे भी महत्वपूर्ण बात यह है कि क्वांटम यांत्रिकी क्या है और यह कैसे काम करता है। इसे विभिन्न स्रोतों से याद किया जा सकता है। मेरा सुझाव है:

• दूर नहीं जाना है, Habr से एक लेख: पुस्तक "क्वांटम यांत्रिकी। सैद्धांतिक न्यूनतम ” ( लियोनार्ड Sasskind और Art Friedman द्वारा इसी नाम की पुस्तक का एक टुकड़ा),
• MFTIshnogo शिक्षक एमजी से भयानक पुस्तक "क्वांटम यांत्रिकी को कैसे समझें" इवानोवा (लिंक से डाउनलोड के लिए उपलब्ध),
• चुना में dxdy फोरम पर , कई पोस्ट हैं जो क्वांटम के सार को अच्छी तरह से समझाते हैं ,
• Lurke पर काफी उपयुक्त समीक्षा और ऐतिहासिक लेख ,
• वैसे तो सारा कचरा इंटरनेट पर भी मिलता है।

  वीके से क्वांटम रसायन विज्ञान पर नेटवर्क मैनुअल ।
  

हालांकि, यहां आवश्यक चीजों का एक कट्टर-निचोड़ निचोड़ भी है:


एक प्रोटॉन द्वारा बनाए गए कूलम्ब इलेक्ट्रिक क्षेत्र में एक इलेक्ट्रॉन / म्यूऑन कैसे चलता है, यह जानने के लिए, क्वांटम यांत्रिकी के मूल समीकरण को हल करना होगा: श्रोडिंगर समीकरण। चूंकि विचाराधीन प्रणाली स्थिर है (समय के साथ नहीं बदलती है), यह इसके सरलीकृत संस्करण को हल करने के लिए पर्याप्त है: स्थिर श्रोडिंगर समीकरण, जिसमें रूप है

$$

$$\ underbrace {(overbrace {- \ frac {\ hbar ^ 2} {2m} \ cdot \ left (\ frac {\ आंशिक ^ 2} {\ आंशिक x ^ 2} + \ frac {\ _ आंशिक 2} {} \ आंशिक y ^ 2} + \ frac {\ आंशिक ^ 2} {\ आंशिक z ^ 2} (दाएं)} ^ {\ hat {T}} + \ overbrace {- \ frac {ke ^ 2} {R}} ^ {\ hat {V}})} _ {\ hat {H}} \ psi = E \ psi$$

यह समीकरण एक दूसरे क्रम का आंशिक अंतर समीकरण है, और इसमें हम एक साथ तरंग फ़ंक्शन के लिए खोज करते हैं $$$\ psi (x, y, z)$ सिस्टम की विशिष्ट स्थिति का वर्णन करना और प्रोटॉन के चारों ओर अंतरिक्ष में नकारात्मक कण के "धब्बा" और इस राज्य की ऊर्जा को दिखाना । ई। जादू टोना तय करने वाले कमोबेश हर जगह पाए जा सकते हैं।


लेकिन एक सरल बात: अंतर समीकरणों से परिचित कोई भी व्यक्ति हाइड्रोजन जैसी परमाणु की जमीनी स्थिति का समाधान पा सकता है। हर किसी को डराने के लिए नहीं, इस टुकड़े को बिगाड़ने वाले में निकाल दिया जाता है:


श्रोडिंगर समीकरण को हल करने का नतीजा ऑर्बिटल्स का एक सेट है, जिसका वर्णन तीन पूर्णांकों एन , एल और एम का उपयोग करके किया गया है, जिसे "क्वांटम संख्या" कहा जाता है। इन परिक्रमाओं की ऊर्जाओं पर निर्भरता $$$(n, l, m)$ नीचे दिया गया है (और रसायन विज्ञान में एक शांत संसाधन से बाँझ):

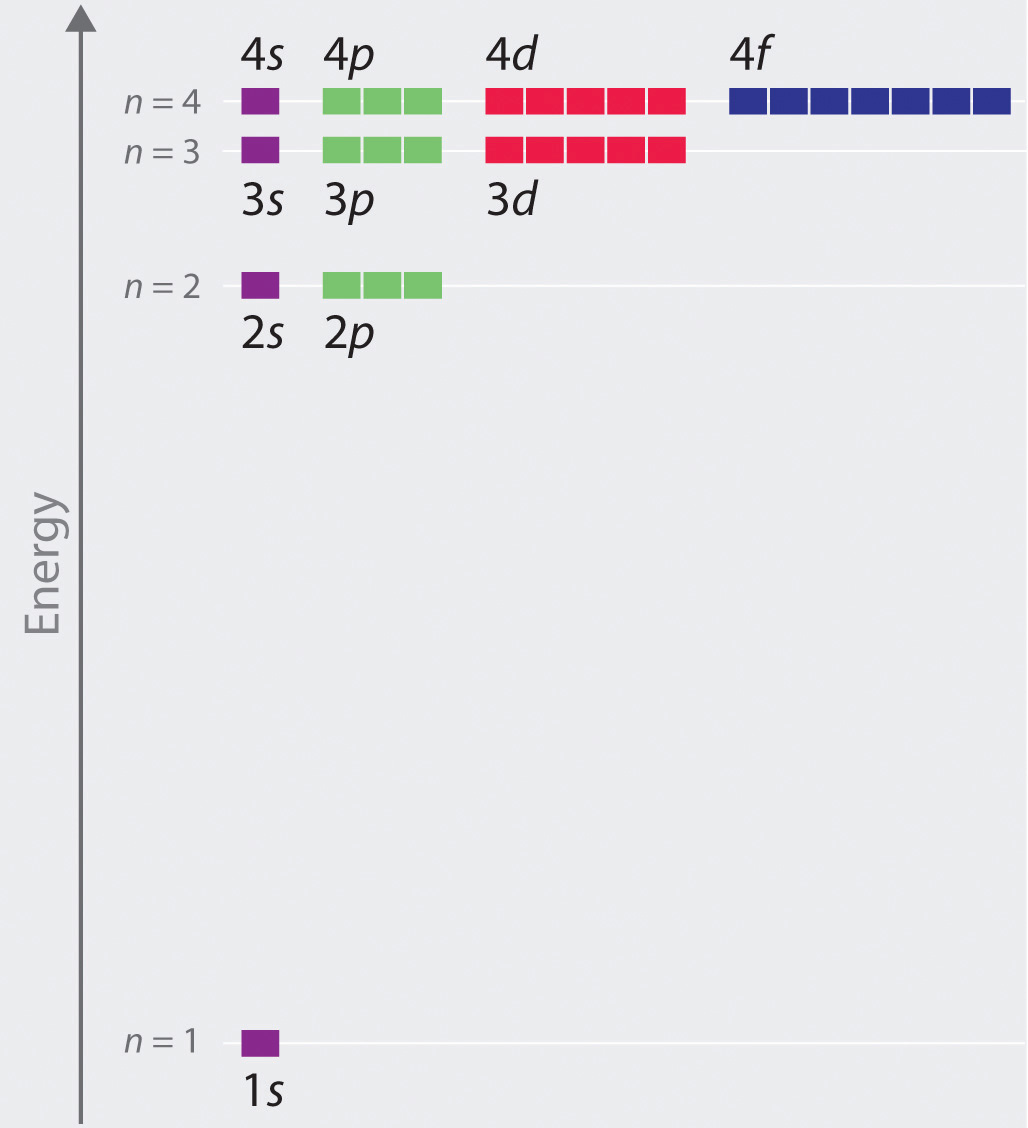
1. पहले नंबर के साथ, n = 1,2,3, ... हम पहले ही मिल चुके हैं। यह तथाकथित है मुख्य क्वांटम संख्या। यह स्तर की ऊर्जा, साथ ही बोहर कक्षा के आकार को निर्धारित करता है। (.. ) «». , / , , — , , , . n =1 n =2 ( ):
   
   
   : , n . , .
2. l , , . n , n ( $$$l = 0, 1,2, \ldots, n$ ). , . , , . , ( $$$\psi=0$ ), , . - ( ):
   
   
   
   «» . , .
   
   
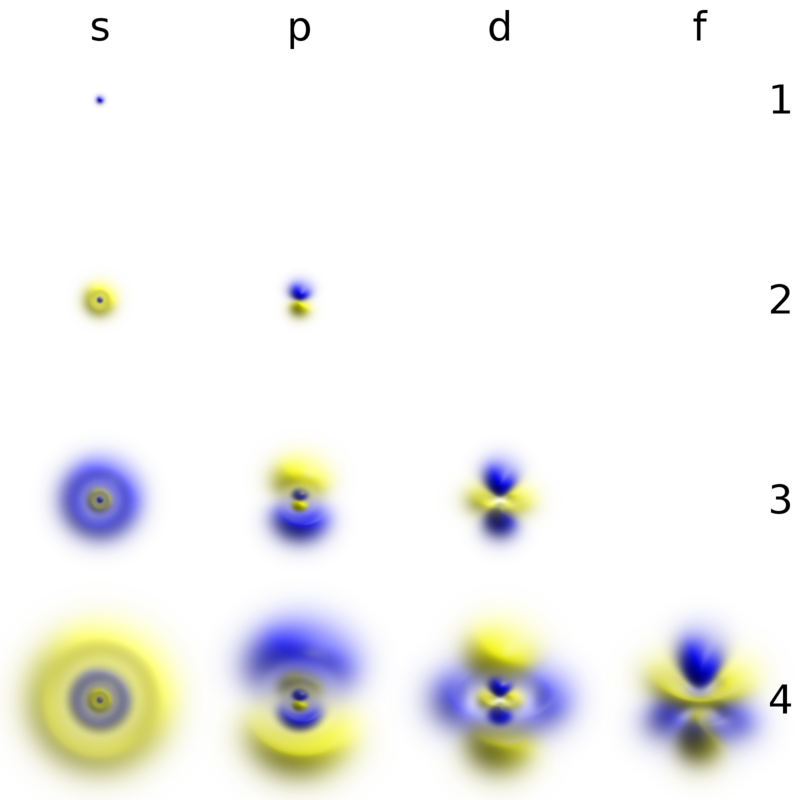
   • $$$l=0$ , , , . s-.
   • ( $$$l=1$ ) p-.
   • 4- $$$l=2$ , d-. .
   • 6- ( $$$l=3$ ) f-.
   • 8- ( $$$l=4$ ) g-.
   • 10- ( $$$l=5$ ) h-.
   • .. आदि
   
   , ( n ) , . : , .
   
3. , m , . . 2l+1 : $$$m = -l, -l+1, \ldots, 0 , \ldots , l-1, l$ .

हमें परिणाम के रूप में क्या मिला: क्वांटम मामले में ऊर्जा बोह्र के समान थी, लेकिन किसी दिए गए एन के लिए संभावित राज्यों की संख्या भी एक परिमित संख्या थी। और यह संख्या बढ़ती हुई कक्षीय ऊर्जा के साथ बढ़ती है। अप्रत्याशित रूप से, लेकिन प्रयोगों के साथ अच्छे समझौते में।

तो हाइड्रोजन परमाणु में क्या अंतर है ( $$$\mathrm{H}^\cdot = \mathrm{p^+ e^-}$ ) अपने म्यूऑन समकक्ष ( $$$\mathrm{p}^+ \mu^-$ )?

अब हम यह समझने के लिए कि फार्मूला लागू किया जाता है, यह समझने के लिए कि हाइड्रोजन परमाणु में एक इलेक्ट्रान को म्यूऑन द्वारा प्रतिस्थापित करने पर वास्तव में क्या बदलता है।

• जमीन की ऊर्जा (यानी, ऊर्जा में न्यूनतम, सबसे स्थिर, जहां से कहीं भी जाने के लिए), मुख्य क्वांटम संख्या n = 1 के साथ। यह सूत्र द्वारा दिया गया है
  

  $$

  $$E_1 = - \frac{m k^2 e^4}{2 \underbrace{n^2}_{1^2} \hbar^2} = - \frac{m k^2 e^4}{2 \hbar^2}$$
  
  जब एक इलेक्ट्रॉन म्यूऑन में स्थानांतरित होता है, केवल द्रव्यमान ( $$$m_{\mu} \approx 207 m_\mathrm{e}$ , — , — ). , 207 : $$$E_1(\mathrm{p}^+\mu^-) = 207 E_1(\mathrm{H}^\cdot)$
  
• . //, . $$$\mathrm{A \rightarrow A^+ + e^-}$ , A — . , $$$\mathrm{A \rightarrow A^+ + \mu^-}$ . . $$$E=0$ . $$$E_n = - \frac{m k^2 e^4}{2{n^2}\hbar^2}$ $$$n \rightarrow + \infty$ . यानी , , / , , - (. ).
  
  , ( $$$E>0$ , ).
  
  , (IP) +/ :
  

  $$

  $$\mathrm{IP} = \underbrace{0}_{\text{ }} - \underbrace{E_1}_{\text{ }} = -E_1$$
  
  , + 207 , , .. «» , .
  
• यहां बोह ऑर्बिट की त्रिज्या भी द्रव्यमान पर निर्भर करती है, और वही त्रिज्या कक्षीय के आकार के लिए अभिव्यक्ति में प्रकट होती है, इसका "आकार" निर्धारित करती है। उदाहरण के लिए, जैसा कि हमने ऊपर देखा, ग्राउंड स्टेट (1s ऑर्बिटल्स) की लहर का रूप है
  

  $$

  $$\psi_{1s}(R) = c\cdot \exp\left(-\frac{R}{R_1} \right)$$
  
  और इसलिए अधिक $$$R_1 = \frac{\overbrace{n^2}^{1^2} \hbar^2 }{mk e^2} = \frac{ \hbar^2 }{mk e^2}$ , तेज़ी से तरंग फ़ंक्शन प्रोटॉन से दूरी के साथ घट जाती है, और इसका छोटा "आकार", अर्थात्। एक नकारात्मक चार्ज कण का स्थानीयकरण। एक इलेक्ट्रॉन से एक म्यूऑन के पास से गुजरते समय, यह त्रिज्या R ₁ 207 के कारक से घटता है; इसलिए, यह पता चलता है कि इलेक्ट्रॉन की तुलना में म्यूऑन प्रोटॉन से अधिक निकटता से जुड़ा हुआ है। और इसलिए, इसे फाड़ना अधिक कठिन है, क्योंकि आयनीकरण अनिवार्य रूप से एक असीम दूर की कक्षा के लिए एक संक्रमण है, अर्थात। प्रोटॉन से बचने के लिए म्यूऑन को इलेक्ट्रॉन से अधिक जाने की आवश्यकता होती है।
  

वैचारिक रूप से, सूत्रों से हमारे सभी निष्कर्ष असीम रूप से सरल हैं: के लिए समस्या को हल करना $$$\ mathrm {H ^ \ cdot}$ और $$$\ mathrm {p} ^ + \ mu ^ -$ वही देखो, लेकिन इस तथ्य के कारण कि म्यूऑन भारी है, यह प्रोटॉन से अधिक चिपक जाता है, और उसके लिए इससे बचना अधिक कठिन होता है।

जाहिर है, है ना? लेकिन सूत्रों के अनुसार यह अभी भी अधिक स्पष्ट है।

आगे क्या होगा?

यह पाठ अगले भाग की तैयारी मात्र थी।

इसमें, हम संलयन के न्यूनतम तापमान को कम करने के लिए प्रस्तावित तंत्र पर सीधे चर्चा करेंगे।

इकाइयों की पुनश्च परमाणु प्रणाली

अंत में, हम एक ऐसी बात पर चर्चा करते हैं जो हमें ऊपर लिखे सभी सूत्रों को सरल बनाएगी। विभिन्न (यहां तक ​​कि स्कूल) कार्यों में, माप की इकाइयों का चुनाव जीवन को सुविधाजनक बना सकता है। और क्वांटम यांत्रिकी के मामले में, इकाइयों की एक बहुत ही सुविधाजनक प्रणाली भी है। यह तथाकथित है इकाइयों की परमाणु प्रणाली । यह प्राकृतिक इकाइयों के वर्ग के अंतर्गत आता है, जो मूल रूप से मानवजनित इकाइयों ( एसआई , जीएचएस ) के विपरीत है, जिसमें मात्राएं जो एक व्यक्ति तुरंत कल्पना कर सकता है, उसे संदर्भ टुकड़ों के रूप में उपयोग किया जाता है। उदाहरण के लिए, एसआई में, लंबाई की इकाई एक मीटर है (लगभग एक वयस्क की एक बांह / पैर की लंबाई), द्रव्यमान - एक किलोग्राम (ओकट्रफेफेस्ट में एक सर्कल में बीयर का द्रव्यमान), यह सब हम रोजमर्रा की जिंदगी में निरीक्षण करते हैं।

इकाइयों की प्राकृतिक प्रणाली, हालांकि, एक आधार के रूप में लेती है जो ज्ञान के संबंधित क्षेत्र में सूत्रों को सरल बनाती है। और परमाणु इकाइयों के मामले में:

• सबसे पहले, सर्वव्यापी प्लांक स्थिरांक को एकता माना जाता है ( $$$\ hbar = 1$ )
• मास इकाई इलेक्ट्रॉन का द्रव्यमान है $$$m_ \ mathrm {e} \ लगभग 9.1 \ गुना 10 ^ {- 31}$ किलो,
• आवेश की इकाई प्रोटॉन आवेश (या, समतुल्य, इलेक्ट्रॉन आवेश मापांक) है $$$e = 1.6 \ गुना 10 ^ {- 19}$ सीएल,
• खैर, एक ही समय में, विद्युत स्थिरांक को इकाई के रूप में लिया जाता है $$$k = \ frac {1} {4 \ pi \ varepsilon_0}$ , जिसके कारण कूलम्ब का नियम रूप लेता है $$$V (R) = \ frac {q_1 q_2} {R}$ ।

इस मामले में, हाइड्रोजन परमाणु के लिए जमीन की स्थिति का बोहर त्रिज्या लंबाई की इकाई बन जाती है $$$a_0 = R_1 = \ frac {\ hbar ^ 2} {m_ \ mathrm {e} k e ^ 2} = 1$ (जैसा कि हम याद करते हैं, यह लगभग 0.5 this है)। ऊर्जा की इकाई को हार्ट्री (डी कोण के हार्टरी के सम्मान में) कहा जाता है, जिसे मान दिया जाता है $$$E_ \ mathrm {h} = \ frac {m_ \ mathrm {e} k ^ 2 e ^ 4} {\ hbar ^ 2} = 1$ । यह देखा गया है कि परमाणु इकाइयों में हाइड्रोजन के 1s स्तर की ऊर्जा 0.5 हार्ट्री है।

अगले भाग में, हम इन इकाइयों में सक्रिय रूप से बैठे रहेंगे।