परिचय:गणितीय भौतिकी के लगभग सभी सबसे महत्वपूर्ण शाखाओं से संबंधित सबसे विविध समस्याओं की एक बड़ी संख्या और सामयिक तकनीकी सवालों के जवाब देने के लिए डिज़ाइन किया गया है जो बेसेल कार्यों के अनुप्रयोग से जुड़ा हुआ है।
बेसेल कार्यों का व्यापक रूप से ध्वनिकी, रेडियोफिज़िक्स, हाइड्रोडायनामिक्स, परमाणु और परमाणु भौतिकी की समस्याओं को हल करने में उपयोग किया जाता है। बेसेल के कई अनुप्रयोग थर्मल चालकता के सिद्धांत और लोच के सिद्धांत (प्लेट कंपन पर समस्याएं, शेल सिद्धांत की समस्याएं, दरारें के पास तनाव की एकाग्रता का निर्धारण करने की समस्याएं) के कई कार्य करते हैं।
बेसेल कार्यों की इस तरह की लोकप्रियता को इस तथ्य से समझाया गया है कि चर के पृथक्करण की शास्त्रीय विधि द्वारा बेलनाकार निर्देशांक में लाप्लास ऑपरेटर वाले गणितीय भौतिकी के समीकरणों को हल करने से एक साधारण अंतर समीकरण होता है, जो इन कार्यों को निर्धारित करने का कार्य करता है [1]।
बेसेल कार्यों का नाम जर्मन खगोल विज्ञानी फ्रेडरिक बेसेल के नाम पर रखा गया है, जिन्होंने 1824 में, सूर्य के चारों ओर ग्रहों की गति का अध्ययन किया, बेसेल कार्यों के लिए पुनरावृत्ति संबंध बनाए गए।
Jv(x) पूर्णांकों के लिए प्राप्त किया
वी एक समारोह का अभिन्न प्रतिनिधित्व
Jv(x) , समारोह के अनगिनत शून्य के अस्तित्व को साबित किया
J0(x) और कार्यों के लिए पहले तालिकाओं को संकलित किया
J1(x) और
J2(x) ।
हालांकि, पहली बार बेसेल के कार्यों में से एक
J0(x) इसे 1732 में डैनियल बर्नोली द्वारा भारी श्रृंखलाओं के दोलन के लिए समर्पित एक काम में वापस माना गया था। डी। बर्नौली ने कार्य की अभिव्यक्ति पाई
J0(x) एक शक्ति श्रृंखला के रूप में और देखा (सबूत के बिना) कि समीकरण
J0(x)=0 अनगिनत मान्य जड़ें हैं।
अगला काम, जिसमें बेसेल कार्यों का सामना किया गया था, 1738 में लियोनार्डो यूलर का काम था, जो एक वृत्ताकार झिल्ली के कंपन के अध्ययन के लिए समर्पित था। इस कार्य में, एल ईयुलर को पूर्णांकों के लिए मिला
वी Bessel फ़ंक्शन अभिव्यक्ति
Jv(x) शक्तियों में एक श्रृंखला के रूप में
x , और बाद के पत्रों में इस अभिव्यक्ति को मनमाना सूचकांक मूल्यों के मामले में बढ़ा दिया
वी । इसके अलावा, एल
वी एक पूर्णांक और एक आधे के बराबर, कार्य करता है
Jv(x) प्राथमिक कार्यों के माध्यम से व्यक्त किया।
उन्होंने नोट किया (बिना सबूत के) कि वैध के साथ
वी कार्यों
Jv(x) अनगिनत असली शून्य हैं और के लिए एक अभिन्न प्रतिनिधित्व दिया
Jv(x) । कुछ शोधकर्ताओं का मानना है कि बेसेल कार्यों और गणितीय भौतिकी में उनके अनुप्रयोगों से संबंधित मुख्य परिणाम एल। यूलर के नाम से जुड़े हैं।
Bessel फ़ंक्शन की संपत्ति का अध्ययन करने के लिए और Bessel फ़ंक्शन के लिए कम किए गए समीकरणों को हल करने के लिए मास्टर विधियों के लिए एक ही समय में, प्रतीकात्मक गणित SymPy - पायथन लाइब्रेरी के स्वतंत्र रूप से वितरित कार्यक्रम की अनुमति देता है।
SymPy प्रतीकात्मक गणित कार्यक्रम में, एक श्रृंखला की राशि के लिए संबंध का उपयोग करके पहले प्रकार के पूर्णांक आदेशों के बेसेल कार्यों के ग्राफ का निर्माण किया जा सकता है:
Jp(x)= sum inftym=0 fracx2m+p(−1)m22m+pm! Gamma(p+m+1)
पहली तरह के बेसेल कार्यfrom sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{p}(x)" p1=plot(besselj(0,x),(x,-20,20),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(1,x),(x,-20,20),line_color='g',show=False) p3=plot(besselj(2,x),(x,-20,20),line_color='r',show=False) p4=plot(besselj(3,x),(x,-20,20),line_color='c',show=False) p1.extend(p2) p1.extend(p3) p1.extend(p4) p1.show()
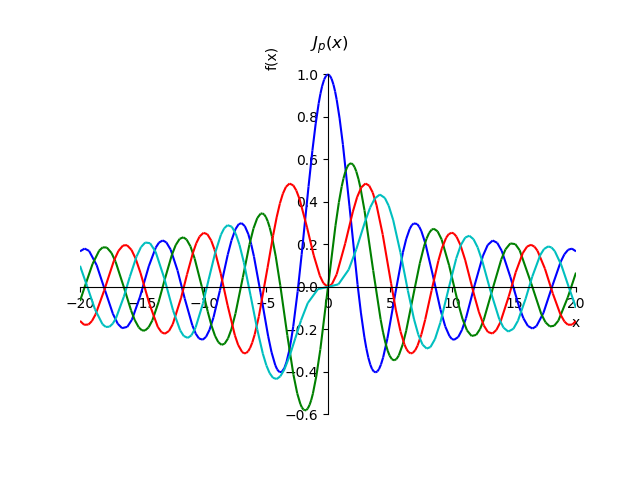
किसी श्रृंखला की राशि के लिए संबंध का उपयोग करते हुए, हम पूरे आदेशों के लिए इन कार्यों की संपत्ति साबित कर सकते हैं
J1(x)=−J−1(x):
पहली तरह के बेसेल फ़ंक्शन की संपत्ति from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1}(x)=-J_{-1}(x)" p1=plot(besselj(1,x),(x,-10,10),line_color='b',title=' $'+st+ '$',show=False) p2=plot(besselj(-1,x),(x,-10,10),line_color='r',show=False) p1.extend(p2) p1.show()

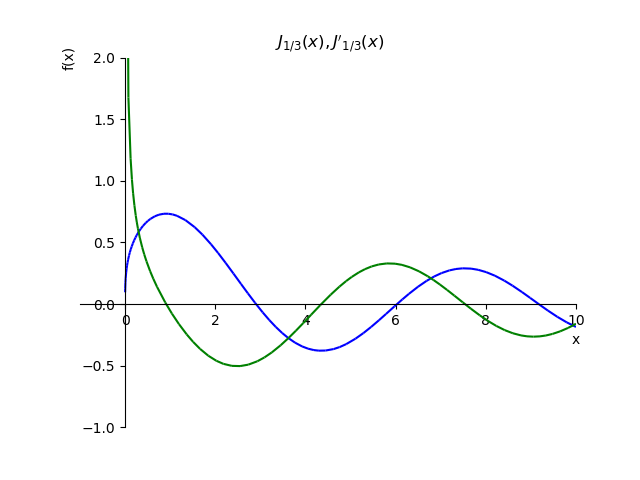
कॉची स्थितियों को प्रदर्शित करने के लिए, हम एक फ़ंक्शन का निर्माण करते हैं
J1/3(x) और इसके व्युत्पन्न
fracdJ1/3(x)dx: :
आंशिक क्रम समारोह और इसके व्युत्पन्न from sympy import* from sympy.plotting import plot x,n, p=var('x,n, p') def besselj(p,x): return summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]) st="J_{1/3}(x),J{}'_{1/3}(x)" p1=plot(besselj(1/3,x),(x,-1,10),line_color='b',title=' $'+st+ '$',ylim=(-1,2),show=False) def dbesselj(p,x): return diff(summation(((-1)**n*x**(2*n+p))/(factorial(n)*gamma(n+p+1)*2**(2*n+p)),[n,0,oo]),x) p2=plot(dbesselj(1/3,x),(x,-1,10),line_color='g',show=False) p1.extend(p2) p1.show()
हालांकि, व्यावहारिक गणना के लिए, अद्भुत mpmath मॉड्यूल का उपयोग किया जाता है, जो न केवल पहली और दूसरी तरह के बेसेल कार्यों के साथ संख्यात्मक रूप से हल करने वाले समीकरणों को अनुमति देता है, जिसमें सभी स्वीकार्य आदेशों के संशोधित वाले भी शामिल हैं, लेकिन स्वचालित सेटिंग के साथ रेखांकन का भी निर्माण करते हैं।
इसके अलावा, mpmath मॉड्यूल को सांकेतिक और संख्यात्मक गणित साझा करने के लिए विशेष उपकरणों की आवश्यकता नहीं होती है। इस मॉड्यूल के निर्माण का इतिहास और उलटा लाप्लास परिवर्तन के लिए इसके उपयोग की संभावना जिसे मैंने पहले ही प्रकाशन में माना है [2]। अब हम बेसेल कार्यों [3] के साथ काम करने के लिए mpmath की चर्चा जारी रखते हैं।
पहली तरह का बेसेल फंक्शन JN(x)mpmath.besselj (n, x, व्युत्पन्न = 0) - पहली तरह का एक Bessel फ़ंक्शन देता है
Jn(x) । कार्यों
JN(x) निम्नलिखित विभेदक समीकरण का हल है:
x2y″+xy′+(x2−n2)y=0
पूरे सकारात्मक के लिए
एन एक साइन या कोसाइन की तरह व्यवहार करता है, एक गुणांक द्वारा गुणा किया जाता है जो धीरे-धीरे घटता है
x rightarrow pm inftyपहली तरह का बेसेल फंक्शन
JN(x) हाइपरजोमेट्रिक फ़ंक्शन का एक विशेष मामला है
oF1 :
J_ {n} (x) = \ frac {x ^ {n}} {2 ^ {n} \ Gamma (n + 1)} {o} F_ {1} (n + 1, \ frac {x ^}} 2}} {4})
बेसेल फ़ंक्शन को विभेदित किया जा सकता है
एम समय प्रदान किया गया है कि mth व्युत्पन्न शून्य के बराबर नहीं है:
fracdmdxmJn(x)
पहली तरह का बेसेल फंक्शन
JN(x) सकारात्मक पूर्णांक आदेशों के लिए n = 0,1,2,3 - बेसेल समीकरण का हल:
from mpmath import* j0 = lambda x: besselj(0,x) j1 = lambda x: besselj(1,x) j2 = lambda x: besselj(2,x) j3 = lambda x: besselj(3,x) plot([j0,j1,j2,j3],[0,14]

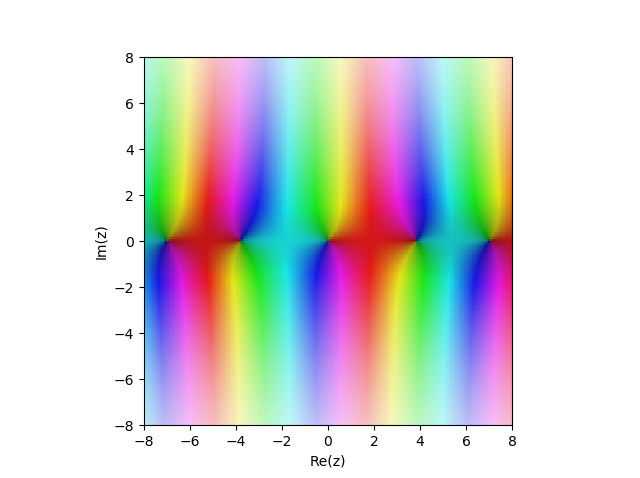
पहली तरह का बेसेल फंक्शन
JN(x) जटिल विमान में:
from sympy import* from mpmath import* cplot(lambda z: besselj(1,z), [-8,8], [-8,8], points=50000)
उदाहरण:
समारोह
बेसेलज(एन,एक्स) दिए गए अंकों की संख्या के साथ एक परिणाम प्रदान करता है
(mp.dps) अल्पविराम के बाद:
from mpmath import* mp.dps = 15; mp.pretty = True print(besselj(2, 1000)) nprint(besselj(4, 0.75)) nprint(besselj(2, 1000j)) mp.dps = 25 nprint( besselj(0.75j, 3+4j)) mp.dps = 50 nprint( besselj(1, pi))
एक फ़ंक्शन तर्क एक बड़ी संख्या हो सकती है:
from mpmath import* mp.dps = 25 nprint( besselj(0, 10000)) nprint(besselj(0, 10**10)) nprint(besselj(2, 10**100)) nprint( besselj(2, 10**5*j))
पहली तरह के बेसेल कार्यों के संबंध में सरल समरूपता को संतुष्ट करते हैं
x=0 :
from sympy import* from mpmath import* mp.dps = 15 nprint([besselj(n,0) for n in range(5)]) nprint([besselj(n,pi) for n in range(5)]) nprint([besselj(n,-pi) for n in range(5)])
जड़ें आवधिक नहीं हैं, लेकिन क्रमिक जड़ों के बीच की दूरी स्पर्शोन्मुख है
2$ । पहली तरह के बेसेल कार्यों में निम्नलिखित कोड होते हैं:
from mpmath import* print(quadosc(j0, [0, inf], period=2*pi)) print(quadosc(j1, [0, inf], period=2*pi))
के लिए
n=1/2 या
n=−1/2 Bessel फ़ंक्शन एक त्रिकोणमितीय फ़ंक्शन में घटाया जाता है:
from sympy import* from mpmath import* x = 10 print(besselj(0.5, x)) print(sqrt(2/(pi*x))*sin(x)) print(besselj(-0.5, x)) print(sqrt(2/(pi*x))*cos(x))
किसी भी ऑर्डर के डेरिवेटिव्स की गणना की जा सकती है,
एकीकरण के लिए नकारात्मक ऑर्डर मेल खाते हैं :
from mpmath import* mp.dps = 25 print(besselj(0, 7.5, 1)) print(diff(lambda x: besselj(0,x), 7.5)) print(besselj(0, 7.5, 10)) print(diff(lambda x: besselj(0,x), 7.5, 10)) print(besselj(0,7.5,-1) - besselj(0,3.5,-1)) print(quad(j0, [3.5, 7.5]))
गैर-पूर्णांक क्रम के साथ भेदभाव , रिमन-लिउविल अंतर अभिन्न के अर्थ में
एक आंशिक व्युत्पन्न देता है , जो फ़ंक्शन का उपयोग करके गणना की जाती है
अंतर() :
from mpmath import* mp.dps = 15 print(besselj(1, 3.5, 0.75)) print(differint(lambda x: besselj(1, x), 3.5, 0.75))
पहली तरह के बेसेल फ़ंक्शन को कॉल करने के अन्य तरीके
mpmath.j0 (x) - बेसेल फ़ंक्शन की गणना करता है
J0(x) ;
mpmath.j1 (x) - बेसेल फ़ंक्शन की गणना करता है
J1(x) ;
दूसरे प्रकार के बेसेल कार्यbessely (n, x, व्युत्पन्न = 0) संबंध से दूसरे प्रकार के बेसेल फ़ंक्शन की गणना करता है:
Yn(x)= fracJn(x)cos( pi cdotn)−J−n(x)sin( pi cdotn)
एक पूर्णांक के लिए
एन निम्नलिखित सूत्र को सीमा के रूप में समझा जाना चाहिए। बेसेल फ़ंक्शन को विभेदित किया जा सकता है
एम समय प्रदान किया गया है कि mth व्युत्पन्न शून्य के बराबर नहीं है:
fracdmdxmYn(x)दूसरे प्रकार का बेसेल फ़ंक्शन
Yn(x) पूर्णांक सकारात्मक आदेश के लिए
n=0,1,2,3 ।
from sympy import* from mpmath import* y0 = lambda x: bessely(0,x) y1 = lambda x: bessely(1,x) y2 = lambda x: bessely(2,x) y3 = lambda x: bessely(3,x) plot([y0,y1,y2,y3],[0,10],[-4,1])
दूसरा प्रकार बेसेल फ़ंक्शन
Yn(x) जटिल विमान में
from sympy import* from mpmath import* cplot(lambda z: bessely(1,z), [-8,8], [-8,8], points=50000)
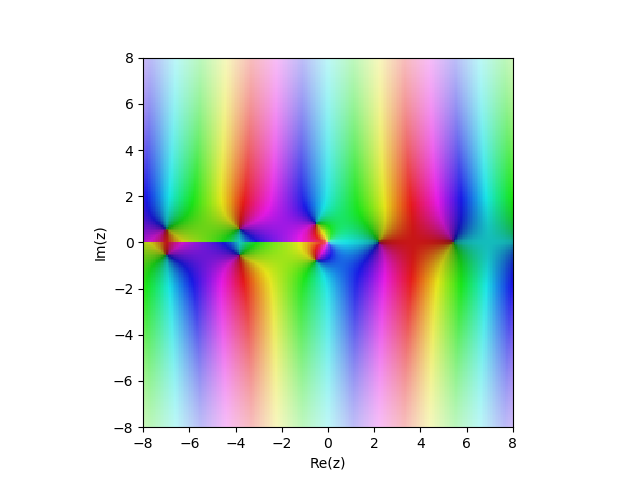
उदाहरण:
कुछ फ़ंक्शन मान
Yn(x) :
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0,0)) print(bessely(1,0)) print(bessely(2,0)) print(bessely(1, pi)) print(bessely(0.5, 3+4j))
तर्क बड़े हो सकते हैं:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(0, 10000)) print(bessely(2.5, 10**50)) print(bessely(2.5, -10**50))
नकारात्मक सहित किसी भी आदेश के डेरिवेटिव की गणना की जा सकती है:
from sympy import* from mpmath import* mp.dps = 25; mp.pretty = True print(bessely(2, 3.5, 1)) print(diff(lambda x: bessely(2, x), 3.5)) print(bessely(0.5, 3.5, 1)) print(diff(lambda x: bessely(0.5, x), 3.5)) print(diff(lambda x: bessely(2, x), 0.5, 10)) print(bessely(2, 0.5, 10)) print(bessely(2, 100.5, 100)) print(quad(lambda x: bessely(2,x), [1,3])) print(bessely(2,3,-1) - bessely(2,1,-1))
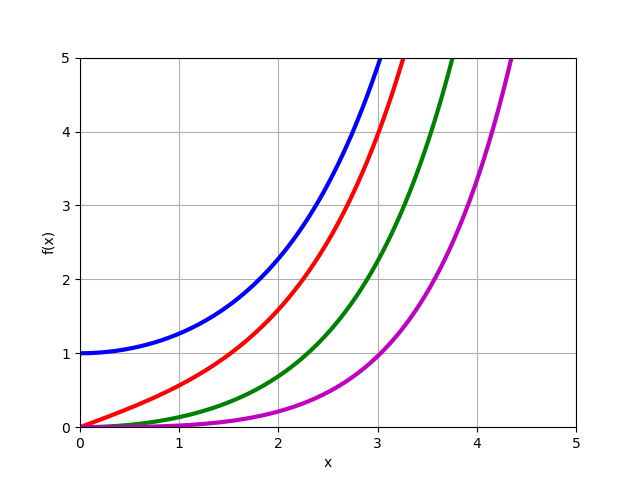
पहली तरह का संशोधित बेसेल फ़ंक्शन
mpmath.besseli(n, x, derivative=0)
बेसेली (n, x, व्युत्पन्न = 0) पहली तरह का संशोधित बेसेल फ़ंक्शन
In(x)= mathiti−nJn(ix)
fracdmdxmIn(x)
संशोधित बेसेल फ़ंक्शन
In(x) वास्तविक आदेशों के लिए
n=0,1,2,3 :
from mpmath import* i0 = lambda x: besseli(0,x) i1 = lambda x: besseli(1,x) i2 = lambda x: besseli(2,x) i3 = lambda x: besseli(3,x) plot([i0,i1,i2,i3],[0,5],[0,5])
संशोधित बेसेल फ़ंक्शन
In(x) जटिल विमान में
from mpmath import* cplot(lambda z: besseli(1,z), [-8,8], [-8,8], points=50000)

उदाहरण:
कुछ अर्थ
In(x) from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(0,0)) print(besseli(1,0)) print(besseli(0,1)) print(besseli(3.5, 2+3j))
तर्क बड़े हो सकते हैं:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 1000)) print(besseli(2, 10**10)) print(besseli(2, 6000+10000j))
पूर्णांक n के लिए, निम्नलिखित अभिन्न प्रतिनिधित्व रखती है:
from mpmath import* mp.dps = 15; mp.pretty = True n = 3 x = 2.3 print(quad(lambda t: exp(x*cos(t))*cos(n*t), [0,pi])/pi) print(besseli(n,x))
किसी भी आदेश के डेरिवेटिव की गणना की जा सकती है:
from mpmath import* mp.dps = 25; mp.pretty = True print(besseli(2, 7.5, 1)) print(diff(lambda x: besseli(2,x), 7.5)) print(besseli(2, 7.5, 10)) print(diff(lambda x: besseli(2,x), 7.5, 10)) print(besseli(2,7.5,-1) - besseli(2,3.5,-1)) print(quad(lambda x: besseli(2,x), [3.5, 7.5]))
दूसरी तरह के संशोधित बेसेल कार्य
mpmath.besselk(n, x)
besselk (n, x) दूसरे प्रकार के बेसेल कार्यों को संशोधित करता है
Kn(x)= frac pi4 fracI−n(x)−In(x)sin( pi cdotn)
एक पूर्णांक के लिए
एन इस सूत्र को एक सीमा के रूप में समझा जाना चाहिए।
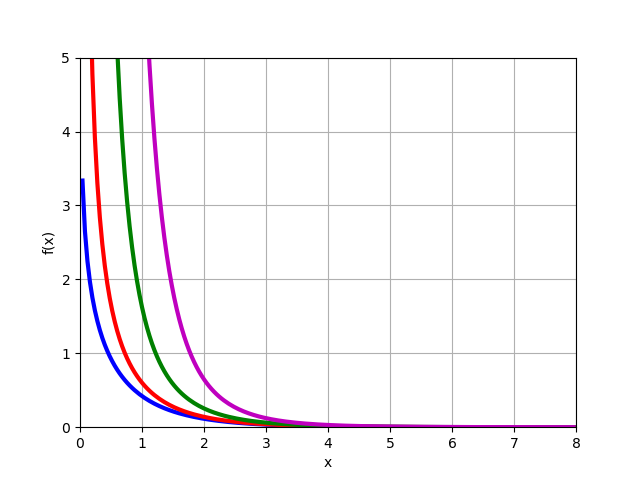
2 तरह का संशोधित बेसेल फ़ंक्शन
Kn(x) सामग्री के लिए
n=0,1,2,3 :
from mpmath import* k0 = lambda x: besselk(0,x) k1 = lambda x: besselk(1,x) k2 = lambda x: besselk(2,x) k3 = lambda x: besselk(3,x) plot([k0,k1,k2,k3],[0,8],[0,5])
2 तरह का संशोधित बेसेल फ़ंक्शन
Kn(x)) जटिल विमान में
from mpmath import* cplot(lambda z: besselk(1,z), [-8,8], [-8,8], points=50000)
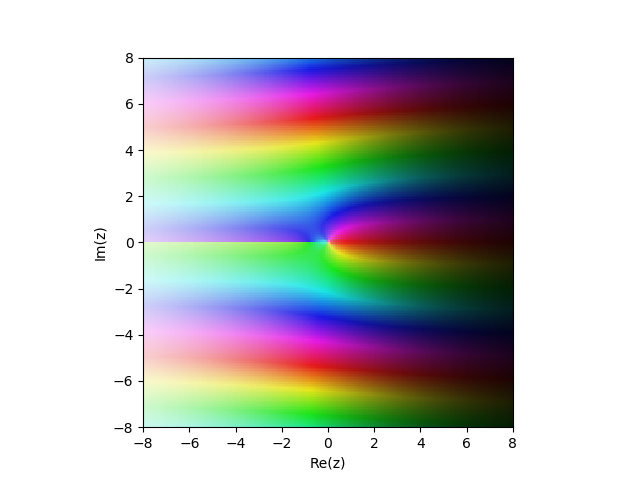
उदाहरण:
जटिल और जटिल तर्क:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0,1)) print(besselk(0, -1)) print(besselk(3.5, 2+3j)) print(besselk(2+3j, 0.5))
तर्क बड़ी संख्या है
from mpmath import * mp.dps = 25; mp.pretty = True print(besselk(0, 100)) print(besselk(1, 10**6)) print(besselk(1, 10**6*j)) print(besselk(4.5, fmul(10**50, j, exact=True)))
एक बिंदु पर एक समारोह के व्यवहार की विशेषताएं
x=0 :
from mpmath import * print(besselk(0,0)) print(besselk(1,0)) for n in range(-4, 5): print(besselk(n, '1e-1000'))
बेसेल फंक्शन जीरो besseljzero() mpmath.besseljzero(v, m, derivative=0)
वास्तविक आदेश के लिए
mathit nu geq0 और एक सकारात्मक पूर्णांक
एम रिटर्न
j n,m , पहले प्रकार के बेसेल फ़ंक्शन का mth धनात्मक शून्य
J nu(z) (देखें
बेसेलज () )। वैकल्पिक रूप से, के साथ
व्युत्पन्न=1 पहला गैर-नकारात्मक प्रधान शून्य देता है
j′ n,m से
J′ nu(z) । अब्रामोविट्ज़ और स्टेगन और डीएलएमएफ का उपयोग करते हुए अनुक्रमण समझौता। एक विशेष मामले पर ध्यान दें।
j′0,1=0 जबकि अन्य सभी शून्य सकारात्मक हैं।
हकीकत में, केवल साधारण शून्य की गणना की जाती है (जब भी हो, तो बेसेल कार्यों के सभी शून्य सरल होते हैं
z=0 ), और
j n,m का एक मोनोटोनिक फ़ंक्शन बन जाता है
n और
एम । विषमताओं के अनुसार शून्य विकल्प:
j′ n,k<j n,k<j′ n,k+1
j n,1<j n+1,2<j n,2<j n+1,2<j n,3 cdots
उदाहरण:
बेसेल कार्यों के अग्रणी शून्य
J0(z) ।
J1(z) ।
J2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1)) print(besseljzero(0,2)) print(besseljzero(0,3)) print(besseljzero(1,1)) print(besseljzero(1,2)) print(besseljzero(1,3)) print(besseljzero(2,1)) print(besseljzero(2,2)) print(besseljzero(2,3))
बेसेल कार्यों के डेरिवेटिव के अग्रणी शून्य
J′0(z) ।
J′1(z) ।
J′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,1,1)) print(besseljzero(0,2,1)) print(besseljzero(0,3,1)) print(besseljzero(1,1,1)) print(besseljzero(1,2,1)) print(besseljzero(1,3,1)) print(besseljzero(2,1,1)) print(besseljzero(2,2,1)) print(besseljzero(2,3,1))
एक बड़े सूचकांक के साथ शून्य:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0,100)) print(besseljzero(0,1000)) print(besseljzero(0,10000)) print(besseljzero(5,100)) print(besseljzero(5,1000)) print(besseljzero(5,10000)) print(besseljzero(0,100,1)) print(besseljzero(0,1000,1)) print(besseljzero(0,10000,1))
एक बड़े आदेश के साथ कार्यों का शून्य:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(50,1)) print(besseljzero(50,2)) print(besseljzero(50,100)) print(besseljzero(50,1,1)) print(besseljzero(50,2,1)) print(besseljzero(50,100,1))
आंशिक क्रम वाले कार्यों का शून्य:
from mpmath import * mp.dps = 25; mp.pretty = True print(besseljzero(0.5,1)) print(besseljzero(1.5,1)) print(besseljzero(2.25,4))
और
J nu(z) । और
J′ nu(z) उनके शून्य पर अनंत उत्पादों के रूप में व्यक्त किया जा सकता है:
from mpmath import * mp.dps = 6; mp.pretty = True v,z = 2, mpf(1) nprint((z/2)**v/gamma(v+1) * \ nprod(lambda k: 1-(z/besseljzero(v,k))**2, [1,inf])) print(besselj(v,z)) nprint((z/2)**(v-1)/2/gamma(v) * \ nprod(lambda k: 1-(z/besseljzero(v,k,1))**2, [1,inf])) print(besselj(v,z,1))
besselyzero() mpmath.besselyzero(v, m, derivative=0)
वास्तविक आदेश के लिए
mathit nu geq0 और एक सकारात्मक पूर्णांक
एम रिटर्न
y n,m ।
एम , Bessel फ़ंक्शन के दूसरे प्रकार के पॉजिटिव शून्य
Y nu(z) (
बाइसली () देखें)। वैकल्पिक रूप से, के साथ
व्युत्पन्न=1 पहला सकारात्मक शून्य देता है
y′ n,m से
Y′ nu(z) । विषमताओं के अनुसार शून्य विकल्प:
y n,k<y′ n,k<y n,k+1
y n,1<y n+1,2<y n,2<y n+1,2<y n,3 cdots
उदाहरण:
बेसेल कार्यों के अग्रणी शून्य
Y0(z) ।
Y1(z) ।
Y2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1)) print(besselyzero(0,2)) print(besselyzero(0,3)) print(besselyzero(1,1)) print(besselyzero(1,2)) print(besselyzero(1,3)) print(besselyzero(2,1)) print(besselyzero(2,2)) print(besselyzero(2,3))
बेसेल कार्यों के डेरिवेटिव के अग्रणी शून्य
Y′0(z) ।
Y′1(z) ।
Y′2(z) from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,1,1)) print(besselyzero(0,2,1)) print(besselyzero(0,3,1)) print(besselyzero(1,1,1)) print(besselyzero(1,2,1)) print(besselyzero(1,3,1)) print(besselyzero(2,1,1)) print(besselyzero(2,2,1)) print(besselyzero(2,3,1))
एक बड़े सूचकांक के साथ शून्य:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0,100)) print(besselyzero(0,1000)) print(besselyzero(0,10000)) print(besselyzero(5,100)) print(besselyzero(5,1000)) print(besselyzero(5,10000)) print(besselyzero(0,100,1)) print(besselyzero(0,1000,1)) print(besselyzero(0,10000,1))
एक बड़े आदेश के साथ कार्यों का शून्य:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(50,1)) print(besselyzero(50,2)) print(besselyzero(50,100)) print(besselyzero(50,1,1)) print(besselyzero(50,2,1)) print(besselyzero(50,100,1))
आंशिक क्रम वाले कार्यों का शून्य:
from mpmath import * mp.dps = 25; mp.pretty = True print(besselyzero(0.5,1)) print(besselyzero(1.5,1)) print(besselyzero(2.25,4))
Bessel फ़ंक्शन अनुप्रयोगबेसेल फ़ंक्शंस का महत्व न केवल अनुप्रयोगों में बेसेल समीकरण की लगातार उपस्थिति के कारण है, बल्कि इस तथ्य के लिए भी है कि कई अन्य सेकंड-ऑर्डर रैखिक अंतर समीकरणों के समाधान को बेसेल फ़ंक्शंस के संदर्भ में व्यक्त किया जा सकता है। यह देखने के लिए कि वे कैसे दिखाई देते हैं, हम ऑर्डर के बेसेल समीकरण से शुरू करते हैं
पी के रूप में:
z2 fracd2wdz2+z fracdwdz+(z2−p2)w=0,(1)
और यहां स्थानापन्न करें
w=x− अल्फा,z=kx beta,(2)
फिर, (2) का उपयोग करते हुए और स्थिरांक का परिचय
ए,बी,सी समीकरण (1) से, हम प्राप्त करते हैं:
x2y′+Axy′+(B+Cxq)y=0,(3)
ए=1−2 अल्फा,बी= अल्फा2− बीटा2पी2,सी= बीटा2k2,क्यू=2 बीटा(४)
समीकरण (4) से हम प्राप्त करते हैं:
\ बाईं \ {\ _ शुरू करें {मैट्रिक्स} \ अल्फा = \ frac {1-A} {2}, \\ \ बीटा = \ frac {q} {2}, \\ k = \ frac {2 \ sqrt {C }} {q} \\ p = \ frac {\ sqrt {(1-A ^ {2} -4B}} {q} \\ \ end {मैट्रिक्स} \ right। (5) $
अगर
C>0 ।
q neq0 ।
(1−A)2 geqslant4B , फिर सामान्य समाधान (के लिए)
x>0 ) समीकरण के (3) के रूप है:
y(x)=x Alpha left[c1Jp(kx beta)+c2J−p(kx beta) सही](6)
जहां:
अल्फा ।
बीटा ।
k सिस्टम (5) से निर्धारित होते हैं। अगर
पी एक पूर्णांक है
Jp द्वारा प्रतिस्थापित किया जाना चाहिए
Yp ।
ऊर्ध्वाधर स्तंभ के अनुदैर्ध्य झुकनेअब हम एक कार्य पर विचार करेंगे जो व्यावहारिक अनुप्रयोगों के लिए महत्वपूर्ण है। इस कार्य में, यह निर्धारित करना आवश्यक है कि कब एक समान ऊर्ध्वाधर स्तंभ अपने स्वयं के वजन के नीचे झुकता है। हम मान लेते हैं
x=0 स्तंभ के ऊपरी ऊपरी छोर में और
x=L>0 इसके आधार पर; हम मानते हैं कि आधार को आधार में (यानी जमीन में) स्थिर रूप से डाला जाता है (अर्थात स्थिर गति से), संभवतः कंक्रीट में।
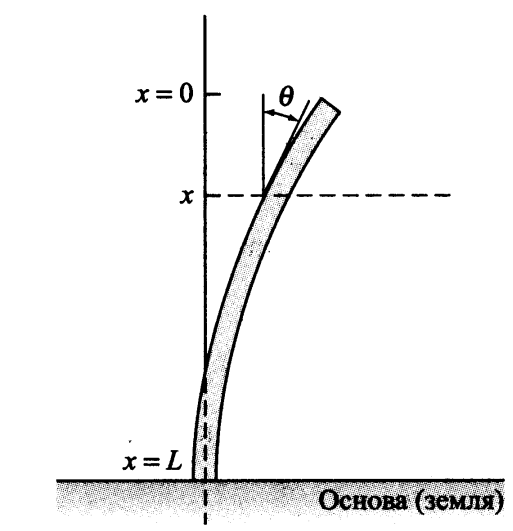
बिंदु पर स्तंभ के कोणीय विचलन को नकारें
x के माध्यम से
थीटा(x) । इन परिस्थितियों में लोच के सिद्धांत से यह निम्नानुसार है:
EI fracd2 थीटाdx2+g rhox theta=0,(7)
जहाँ
ई - कॉलम सामग्री के युवा मापांक,
मैं - इसके पार अनुभाग की जड़ता का क्षण,
rho - स्तंभ का रैखिक घनत्व और
जी - गुरुत्वाकर्षण त्वरण। सीमा की स्थिति फॉर्म के हैं:
थीटा′(0)=0, थीटा(एल)=0,(8)
हम (7) और (8) का उपयोग करके समस्या का समाधान करेंगे:
lambda= Gamma2= fracg rhoEI(9)
हम फिर से लिखना (7) को ध्यान में रखते हुए (9) शर्त के तहत (8):
fracd2 थीटाdx2+ Gamma2x थीटा=0; fracd thetadx=0, theta(L)=0.(10)
एक स्तंभ केवल विकृत हो सकता है यदि समस्या का गैर-तुच्छ समाधान हो (10); अन्यथा, स्तंभ ऊर्ध्वाधर से विचलित नहीं होने की स्थिति में रहेगा (यानी, ऊर्ध्वाधर से विचलन करने में असमर्थ)।
विभेदक समीकरण (10) एक हवादार समीकरण है। समीकरण (10) के लिए समीकरण (3) का रूप है
A=B=0 ।
C= गामा2 ।
q=3 । समीकरणों की प्रणाली (5) से हम प्राप्त करते हैं
अल्फा= frac12 ।
बीटा= frac32 ।
k= frac23 Gamma ।
p= frac13 ।
इसलिए, सामान्य समाधान के रूप हैं:
theta(x)=x1/2 left[c1J1/3( frac23 Gammax3/2)+c2J−1/3( frac23 Gammax3/2) right]।(११)
प्रारंभिक शर्तों को लागू करने के लिए, हम स्थानापन्न करते हैं
p= pm frac13 में
Jp= sum inftym=0 frac(−1)mm! Gamma(p+m+1) left( fracx)2 right)2m+p(12)
परिवर्तन (12) के बाद, खाते के समाधान (11) को ध्यान में रखते हुए, हम प्राप्त करते हैं:
\ theta (x) = \ frac {c_ {1} \ gamma ^ {1/3}} {3 ^ {1/3} \ Gamma (4/3)} \ left (x- \ frac {\ _ gma ^) {2} x ^ {4}} {12} + \ frac {\ _ गामा ^ {4} x ^ {7}} {504} - \ cdot \ cdot \ cdot \ right) + \\ + \ frac {c {{ 2} 3 ^ {1/3}} {\ _ गामा ^ {1/3} \ गामा (\ frac {2} {3})} \ left (1- \ frac {\ n गामा ^ {2} x ^ {3 }} {6} + \ frac {\ _ gma ^ {4} x ^ {6}} {180} - \ cdot \ cdot \ cdot \ right)। (13)
शुरुआती बिंदु पर प्रदान किया गया
थीटा′(0)=0 हमें मिलता है
c1=0 , तो (11) रूप लेता है:
theta(x)=c2x1/2J−1/3( frac23 Gammax3/2),(14)
अंतिम बिंदु पर प्रदान किया गया
theta(L)=0 , (14) हम प्राप्त करते हैं:
J−1/3((frac23 GammaL3/2)=0(15)
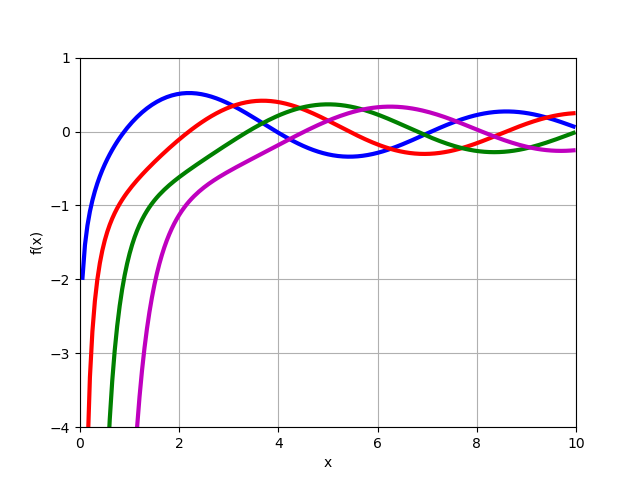
यह ध्यान दिया जाना चाहिए कि यदि कार्यों के ग्राफ का निर्माण किया गया था तो परिवर्तन (13), (14) नहीं किया जा सकता था
J1/3(x),J−1/3(x) mpmath मॉड्यूल की माना क्षमताओं का उपयोग करना:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) f1=lambda x: besselj(1/3,x) plot([f,f1], [0, 15])
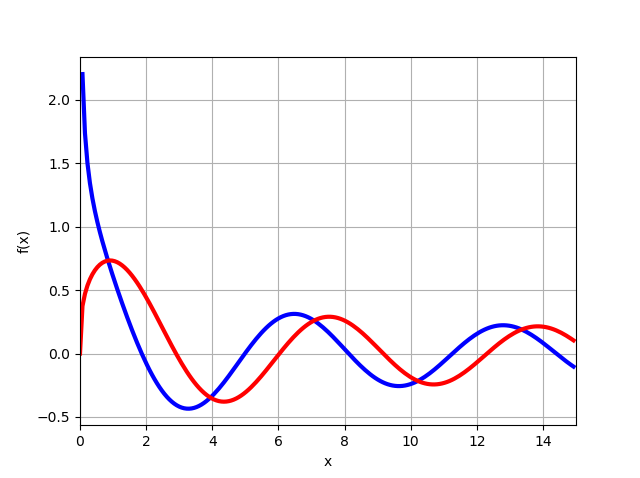
ग्राफ़ से यह इस प्रकार है कि x = 0 फ़ंक्शन के लिए
J1/3(0)=0 और खाते के समाधान (11) को ध्यान में रखते हुए, हम तुरंत आवश्यक समीकरण (15) प्राप्त करते हैं, यह केवल z खोजने के लिए रहता है, जैसा कि नीचे दिखाया गया है।
इस प्रकार, स्तंभ केवल तभी विकृत है
z= frac23 GammaL3/2 समीकरण की जड़ है
J−1/3(z)=0 । एक फ़ंक्शन बनाएँ
J−1/3(z) एक अलग चार्ट पर:
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) plot(f, [0, 15])

ग्राफ से पता चलता है कि पहली जड़ 2. से थोड़ी कम है
z0 समीकरण से
J−1/3(z)=0 आप, खोज बिंदु के अनुसार, खोज, स्वीकार
(खोज, f, z0) फ़ंक्शन का उपयोग कर सकते हैं
x0=1 और छह दशमलव स्थान
mp.dps = 6 :
from mpmath import* mp.dps = 6; mp.pretty = True f=lambda x: besselj(-1/3,x) print("z0=%s"%findroot(f, 1)
हमें मिलता है:
z0=1.86635हम महत्वपूर्ण लंबाई की गणना करते हैं, उदाहरण के लिए, सूत्र (15) का उपयोग करते हुए एक फ्लैगपोल:
अनुभाग में विभिन्न मापदंडों के लिए फ्लैगपोल की ऊंचाई from numpy import* def LRr(R,r): E=2.9*10**11
हमें मिलता है:
8.47 मी
10.25 मी
एक खोखले फ्लैगपोल एक ठोस से अधिक हो सकता है।
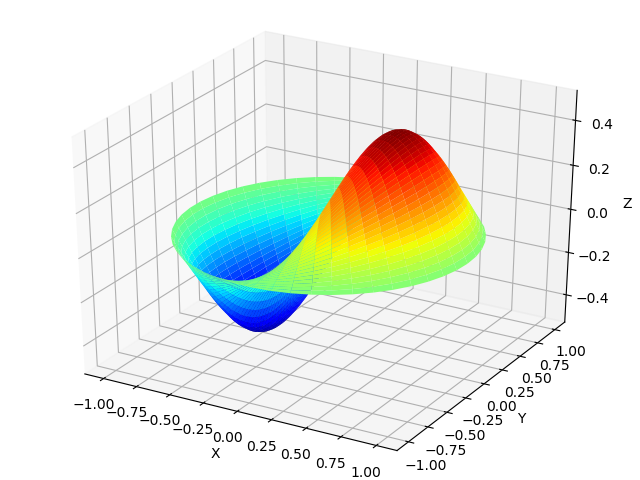
एक पतली झिल्ली में तरंग का प्रसार।
एक पतली झिल्ली जब ध्वनि तरंगें इसमें प्रवेश करती हैं, न केवल तरंगों की आवृत्ति के साथ दोलन करती हैं। झिल्ली कंपन का रूप निम्नलिखित सूची के अनुसार बेसेल कार्यों में प्राप्त किया जा सकता है, सूत्र
बेसेलज () और
बेसेलजेरो () का उपयोग करके:
झिल्ली तरंग from mpmath import* from numpy import* import matplotlib.pyplot as plt from mpl_toolkits.mplot3d import Axes3D from matplotlib import cm def Membrana(r): mp.dps=25 return cos(0.5) * cos( theta) *float(besselj(1,r*besseljzero(1,1) ,0)) theta =linspace(0,2*pi,50) radius = linspace(0,1,50) x = array([r * cos(theta) for r in radius]) y = array([r * sin(theta) for r in radius]) z = array([Membrana(r) for r in radius]) fig = plt.figure("") ax = Axes3D(fig) ax.plot_surface(x, y, z, rstride=1, cstride=1, cmap=cm.jet) ax.set_xlabel('X') ax.set_ylabel('Y') ax.set_zlabel('Z') plt.show()
SciPy लाइब्रेरी के विशेष बेसेल कार्यों में mpmath मॉड्यूल के लिए विकल्प
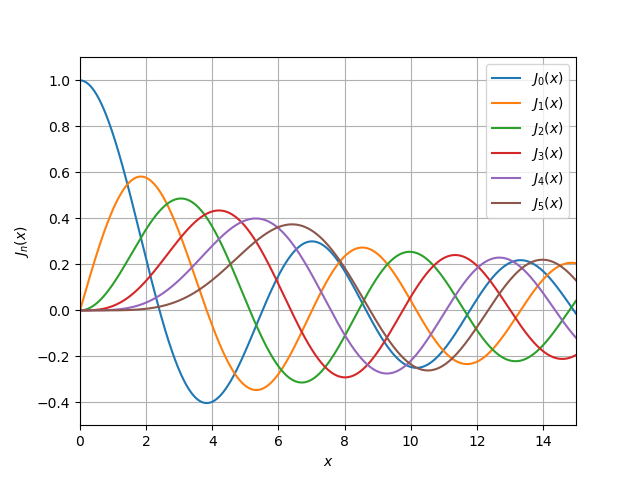
SciPy लाइब्रेरी [4] से बेसेल कार्यों की विस्तृत चर्चा में देरी किए बिना, मैं पहली और दूसरी तरह के
jv (v, x) ,
yv (v, x) के कार्यों को प्लॉट करने के लिए केवल दो सूचियाँ दूंगा:
jv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.jv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$J_{0}(x)$', '$ J_{1}(x)$', '$J_{2}(x)$', '$J_{3}(x)$', '$ J_{4}(x)$','$ J_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('${J}_n(x)$') py.grid(True) py.show()
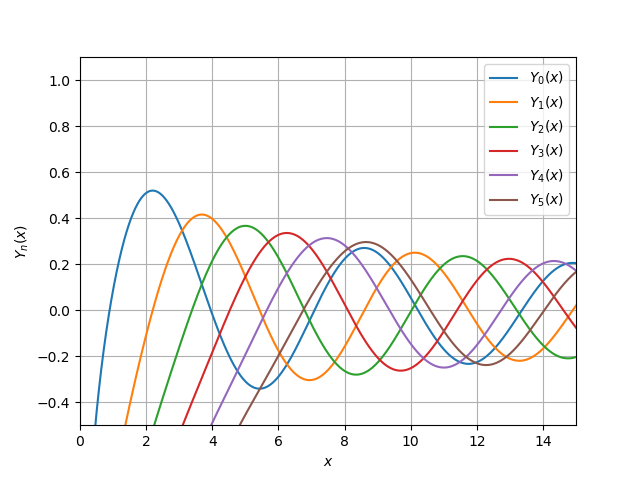
yv (v, x) import numpy as np import pylab as py import scipy.special as sp x = np.linspace(0, 15, 500000) for v in range(0, 6): py.plot(x, sp.yv(v, x)) py.xlim((0, 15)) py.ylim((-0.5, 1.1)) py.legend(('$Y_{0}(x)$', '$ Y_{1}(x)$', '$Y_{2}(x)$', '$Y_{3}(x)$', '$ Y_{4}(x)$','$ Y_{5}(x)$'), loc = 0) py.xlabel('$x$') py.ylabel('$Y_{n}(x)$') py.grid(True) py.show()
निष्कर्ष:
लेख मेस्मैथ, सिम्पी और स्केपी पुस्तकालयों का उपयोग करते हुए बेसेल कार्यों के साथ काम करने की मूल बातों का वर्णन करता है, अंतर समीकरणों को हल करने के लिए फ़ंक्शंस का उपयोग करने के उदाहरण प्रदान करता है। लेख गणितीय भौतिकी के समीकरणों के अध्ययन में उपयोगी हो सकता है।
संदर्भ:
1.
बेसेल फंक्शंस2.
नियंत्रण प्रणाली के गतिशील लिंक का विश्लेषण करने के लिए उलटा लाप्लास परिवर्तन का उपयोग करना3.
Bessel फ़ंक्शन संबंधित कार्य4.
विशेष कार्य (scipy.special)।