🚱 🛀🏼 💤 जानकारी के नुकसान के बिना प्रयोगात्मक डेटा के नमूना आकार में कमी ✋🏿 🍚 👩🏼‍🤝‍👨🏾

प्रायोगिक डेटा हिस्टोग्राम की समस्या क्या है

किसी भी औद्योगिक उद्यम के उत्पाद गुणवत्ता प्रबंधन का आधार उनके बाद के प्रसंस्करण के साथ प्रयोगात्मक डेटा का संग्रह है।

प्रायोगिक परिणामों की प्रारंभिक प्रक्रिया में डेटा के वितरण के कानून के बारे में परिकल्पना की तुलना करना शामिल है, जो वर्णन करता है, सबसे छोटी त्रुटि के साथ, देखे गए नमूने पर एक यादृच्छिक चर।

इसके लिए, सैंपल को हिस्टोग्राम के रूप में प्रस्तुत किया जाता है

k

$k$ लंबाई के अंतराल पर निर्मित स्तंभ

ड

$ड$ ।

माप परिणामों के वितरण के आकार की पहचान के लिए कई समस्याओं की भी आवश्यकता होती है जिनकी समाधान दक्षता अलग-अलग वितरणों के लिए भिन्न होती है (उदाहरण के लिए, कम से कम वर्ग विधि का उपयोग करके या एन्ट्रापी अनुमानों की गणना करना)।

इसके अलावा, वितरण की पहचान भी आवश्यक है क्योंकि सभी अनुमानों का बिखरना (मानक विचलन, अतिरिक्त, कुर्टोसिस, आदि) भी वितरण कानून के रूप पर निर्भर करता है।

प्रयोगात्मक डेटा के वितरण फॉर्म की पहचान करने की सफलता नमूना आकार पर निर्भर करती है और, यदि यह छोटा है, तो वितरण सुविधाओं को नमूना के यादृच्छिकता से नकाब लगाया जाता है। व्यवहार में, बड़े नमूने का आकार प्रदान करना संभव नहीं है, उदाहरण के लिए, विभिन्न कारणों से 1000 से अधिक।

ऐसी स्थिति में, अंतराल में नमूना डेटा को सबसे अच्छे तरीके से वितरित करना महत्वपूर्ण है, जब अंतराल श्रृंखला आगे के विश्लेषण और गणना के लिए आवश्यक है।

इसलिए, सफल पहचान के लिए, अंतराल की संख्या असाइन करने की समस्या को हल करना आवश्यक है k

A. पुस्तक में हल्द [1] बड़े पैमाने पर आश्वस्त करता है कि समूह अंतराल की एक इष्टतम संख्या है जब इन अंतरालों पर निर्मित हिस्टोग्राम का स्टेपवाइज लिफाफा सामान्य आबादी के सुचारू वितरण वक्र के सबसे करीब होता है।

इष्टतम से संपर्क करने के व्यावहारिक संकेतों में से एक हिस्टोग्राम में डिप्स का गायब होना है, और फिर सबसे बड़ी कश्मीर को इष्टतम के करीब माना जाता है, जिस पर हिस्टोग्राम अभी भी एक चिकनी चरित्र को बरकरार रखता है।

जाहिर है, हिस्टोग्राम का प्रकार एक यादृच्छिक चर से संबंधित अंतराल के निर्माण पर निर्भर करता है, हालांकि, समान विभाजन के मामले में, इस तरह के निर्माण का एक संतोषजनक तरीका अभी भी उपलब्ध नहीं है।

विभाजन, जिसे सही माना जा सकता था, इस तथ्य की ओर जाता है कि कथित रूप से निरंतर वितरण घनत्व (हिस्टोग्राम) के टुकड़े के निरंतर कार्य द्वारा सन्निकटन त्रुटि न्यूनतम होगी।

कठिनाइयाँ इस तथ्य के कारण होती हैं कि अनुमानित घनत्व अज्ञात है, इसलिए, अंतराल की संख्या अंतिम नमूने के आवृत्ति वितरण के रूप को दृढ़ता से प्रभावित करती है।

एक निश्चित नमूना लंबाई के लिए, विभाजन अंतराल के विस्तार से न केवल उन्हें प्राप्त करने की अनुभवजन्य संभावना का शोधन होता है, बल्कि सूचना के एक अपरिहार्य नुकसान (दोनों सामान्य अर्थों और संभावित घनत्व वितरण वक्र के अर्थ में) की ओर जाता है, इसलिए, आगे अनुचित वृद्धि के साथ, अध्ययन किया गया वितरण बहुत अधिक सुचारू है। ।

एक बार जब यह उत्पन्न हो जाता है, तो हिस्टोग्राम के तहत सीमा को विभाजित करने का कार्य विशेषज्ञों के दृष्टिकोण से गायब नहीं होता है, और जब तक इसके समाधान पर एकमात्र स्थापित राय प्रकट नहीं होती है, तब तक कार्य प्रासंगिक रहेगा।

प्रयोगात्मक डेटा के हिस्टोग्राम की गुणवत्ता का मूल्यांकन करने के लिए मानदंडों का विकल्प

पियर्सन की कसौटी, जैसा कि आप जानते हैं, नमूने को अंतराल में विभाजित करने की आवश्यकता है - यह उन में है कि अपनाया मॉडल और तुलना किए गए नमूने के बीच अंतर का मूल्यांकन किया जाता है।

c h i^{2} = s u m_{j = 1}^{m} f r a c (E_{j} - M_{j})^{2} M_{j}

$\ chi ^ {2} = \ sum_ {j = 1} ^ {m} \ frac {(E_ {j} -M_ {j}) ^ {2}} {M_ {j}}$

जहां:

E_{j}

$E_ {j}$ - प्रयोगात्मक आवृत्तियों

(n_{j})

$(n_ {j})$ ;

M_{j}

$M_ {j}$ - एक ही कॉलम में आवृत्ति मान; हिस्टोग्राम कॉलम की मी-संख्या।

हालांकि, निरंतर लंबाई के अंतराल के मामले में इस कसौटी के आवेदन, आमतौर पर हिस्टोग्राम का निर्माण करने के लिए उपयोग किया जाता है, अक्षम है। इसलिए, पियर्सन मानदंड की प्रभावशीलता पर काम करता है, अंतराल को समान लंबाई के साथ नहीं माना जाता है, लेकिन स्वीकृत मॉडल के अनुसार समान संभावना के साथ।

इस मामले में, हालांकि, समान लंबाई के अंतराल की संख्या और समान संभावना के अंतराल की संख्या कई बार (समान रूप से संभावित वितरण के अपवाद के साथ) से भिन्न होती है, जो किसी को [2] में प्राप्त परिणामों की विश्वसनीयता पर संदेह करने की अनुमति देती है।

निकटता मानदंड के रूप में, एन्ट्रापी गुणांक का उपयोग करना उचित है, जिसकी गणना निम्नानुसार की जाती है: [३]

k_{e} = f r a c d n 2 s i g m a 10^{b e t a}

$k_ {e} = \ frac {dn} {2 \ sigma} 10 ^ {\ beta}$

ब ी ट ा = - f r a c 1 n s u m_{i = 1}^{m} n_{i} l g (n_{i})

$\ बीटा = - \ frac {1} {n} \ sum_ {i = 1} ^ {m} {n_ {i} lg (n_ {i})}$

जहां:

n_{i}

$n_ {i}$ - आई-वें अंतराल में टिप्पणियों की संख्या

i = 0, . . ., m

$i = 0, ..., m$

एन्ट्रापी गुणांक और numpy.istist मॉड्यूल का उपयोग करके प्रयोगात्मक डेटा के हिस्टोग्राम की गुणवत्ता का आकलन करने के लिए एल्गोरिदम

मॉड्यूल का उपयोग करने के लिए सिंटैक्स निम्नानुसार है:

numpy.histogram (ए, डिब्बे = मीटर, रेंज = कोई नहीं, आदर्श = कोई नहीं, वजन = कोई नहीं, घनत्व = कोई भी नहीं)

हम numpy.histogram मॉड्यूल में लागू हिस्टोग्राम बंटवारे के अंतराल की अधिकतम संख्या मीटर खोजने के तरीकों पर विचार करेंगे:

• 'ऑटो' - 'स्टर्गेस' और 'एफडी' की अधिकतम रेटिंग, अच्छा प्रदर्शन प्रदान करती है;
• 'एफडी' (फ्रीडमैन डायकोनिस एस्टिमेटर) - एक विश्वसनीय (उत्सर्जन-प्रतिरोधी) मूल्यांकनकर्ता जो डेटा की परिवर्तनशीलता और आकार को ध्यान में रखता है;
• 'doane' - स्टर्गेस अनुमान का एक उन्नत संस्करण जो गैर-सामान्य वितरण के साथ डेटा सेट के साथ अधिक सटीक रूप से काम करता है;
• 'स्कॉट' एक कम विश्वसनीय मूल्यांकनकर्ता है जो डेटा की परिवर्तनशीलता और आकार को ध्यान में रखता है;
• 'पत्थर' - मूल्यांकनकर्ता त्रुटि के वर्ग के अनुमान के क्रॉस-चेक पर आधारित है, इसे स्कॉट के शासन के सामान्यीकरण के रूप में माना जा सकता है;
• 'चावल' - मूल्यांकनकर्ता परिवर्तनशीलता को ध्यान में नहीं रखता है, लेकिन केवल डेटा का आकार, अक्सर अंतराल की आवश्यक संख्या की संख्या को कम कर देता है;
• 'स्टर्ज' - विधि (डिफ़ॉल्ट रूप से), केवल डेटा के आकार को ध्यान में रखते हुए, केवल गॉसियन डेटा के लिए इष्टतम है और बड़े गैर-गॉसियन डेटा सेट के लिए अंतराल की संख्या को कम करके आंका जाता है;
• 'sqrt' अंतर की संख्या के त्वरित और आसान गणना के लिए Excel और अन्य कार्यक्रमों द्वारा उपयोग किए जाने वाले डेटा आकार के लिए वर्गमूल अनुमानक है।

एल्गोरिथ्म का वर्णन शुरू करने के लिए, हम एंट्रॉपी गुणांक और एन्ट्रापी त्रुटि की गणना करने के लिए numpy.histogram () मॉड्यूल को अनुकूलित करते हैं:

from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#       m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#  ke=h/std (a)#    (1). return ke,h

अब एल्गोरिथ्म के मुख्य चरणों पर विचार करें:

1) हम एक नियंत्रण नमूना बनाते हैं (बाद में "बड़े नमूने" के रूप में संदर्भित) जो प्रायोगिक डेटा को संसाधित करने में त्रुटि के लिए आवश्यकताओं को पूरा करता है । एक बड़े नमूने से, सभी विषम सदस्यों को हटाकर, हम एक छोटा नमूना बनाते हैं (बाद में इसे "छोटा नमूना" कहा जाता है);

2) सभी मूल्यांकनकर्ताओं के लिए 'ऑटो', 'fd', 'doane', 'scott', 'stone', 'rice', 'Sterges', 'sqrt' हम एंट्रॉपी गुणांक ke1 की गणना करते हैं और एक बड़े नमूने से त्रुटि 1 और एंट्रॉपी गुणांक ke2 और एक छोटे नमूने के लिए त्रुटि h2, साथ ही अंतर का पूर्ण मूल्य - abs (ke1-ke2);

3) कम से कम चार अंतराल के स्तर पर मूल्यांकनकर्ताओं के संख्यात्मक मूल्यों को नियंत्रित करते हुए, हम मूल्यांकनकर्ता का चयन करते हैं जो पूर्ण अंतर का न्यूनतम मूल्य प्रदान करता है - abs (ke1-ke2)।

4) एक मूल्यांकक की पसंद पर अंतिम निर्णय के लिए, हम एक एब्सट्रैक्ट पर निर्माण करते हैं, जिसमें बड़े और छोटे नमूनों के लिए वितरण होते हैं, जिसमें न्यूनतम अनुपलब्ध मूल्य (ke1-ke2) प्रदान करते हैं, और दूसरे पर मूल्यांकक के साथ अधिकतम पेट मूल्य (ke1-ke2) प्रदान करते हैं। दूसरे हिस्टोग्राम में एक छोटे से नमूने में अतिरिक्त छलांग की उपस्थिति पहले में मूल्यांकनकर्ता की सही पसंद की पुष्टि करती है।

एक प्रकाशन [2] से डेटा के नमूने पर प्रस्तावित एल्गोरिदम के काम पर विचार करें। डेटा को उनके द्रव्यमान के बाद के माप के साथ 500 से 80 रिक्त स्थान का चयन करके यादृच्छिक रूप से प्राप्त किया गया था। वर्कपीस में निम्नलिखित सीमा में द्रव्यमान होना चाहिए:

m = 17_{- 0.4}^{+ 0.6}

$m = 17 _ {- 0.4} ^ {+ 0.6}$ किलो। हम निम्नलिखित सूची का उपयोग करके इष्टतम हिस्टोग्राम मापदंडों का निर्धारण करते हैं:

लिस्टिंग

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h a =array([17.37, 17.06, 16.96, 16.83, 17.34, 17.45, 17.60, 17.30, 17.02, 16.73, 17.08, 17.28, 17.08, 17.21, 17.29,17.47, 16.84, 17.39, 16.95, 16.92, 17.59, 17.28, 17.31, 17.25, 17.43,17.30, 17.18, 17.26, 17.19, 17.09,16.61, 17.16, 17.17, 17.06, 17.09,16.83, 17.17, 17.06, 17.59, 17.37,17.09, 16.94, 16.76, 16.98, 16.70, 17.27, 17.48, 17.21, 16.74, 17.12,17.33, 17.15, 17.56, 17.45, 17.49,16.94, 17.28, 17.09, 17.39, 17.05, 16.97, 17.16, 17.38, 17.23, 16.87,16.84, 16.94, 16.90, 17.27, 16.93,17.25, 16.85, 17.41, 17.37, 17.50,17.13, 17.16, 17.05, 16.68, 17.56 ] ) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=80) : %s"%round(std(a),3)) print("    (n=80):%s"%round(mean(a),3)) print("     (n=40): %s"%round(std(b),3)) print("   (n=40): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

हमें मिलता है:

नमूने के लिए मानक विचलन (n = 80): 0.24
नमूने के लिए गणितीय अपेक्षा (एन = 80): 17.158
नमूने के लिए मानक विचलन (n = 40): 0.202
नमूने की गणितीय अपेक्षा (n = 40): 17.138
ke1 = 1.95, h1 = 0.467, ke2 = 1.917, h2 = 0.387, dke = 0.033, m = ऑटो
ke1 = 1.918, h1 = 0.46, ke2 = 1.91, h2 = 0.386, dke = 0.008, m = fd
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = doane
ke1 = 1.918, h1 = 0.46, ke2 = 1.91, h2 = 0.386, dke = 0.008, m = स्कॉट
ke1 = 1.898, h1 = 0.455, ke2 = 1.934, h2 = 0.39, dke = 0.036, m = पत्थर
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, मी = चावल
ke1 = 1.95, h1 = 0.467, ke2 = 1.917, h2 = 0.387, dke = 0.033, m = स्टर्ज
ke1 = 1.831, h1 = 0.439, ke2 = 1.917, h2 = 0.387, dke = 0.086, m = sqrt

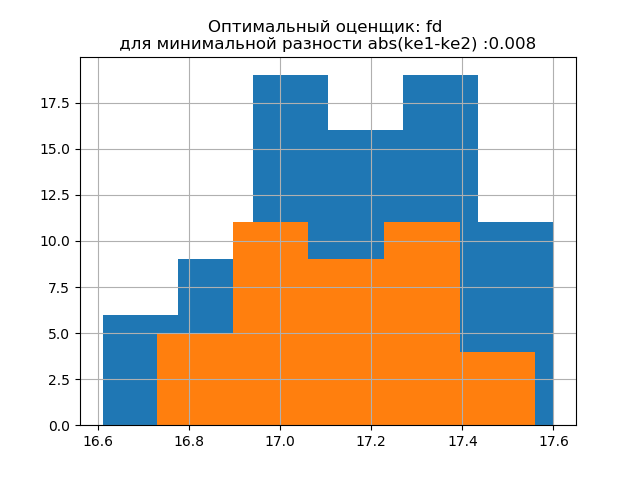
एक बड़े नमूने का वितरण फॉर्म छोटे नमूने के वितरण फॉर्म के समान है। स्क्रिप्ट से निम्नानुसार, 'fd' एक विश्वसनीय (उत्सर्जन-प्रतिरोधी) मूल्यांकनकर्ता है जो डेटा की परिवर्तनशीलता और आकार को ध्यान में रखता है। इस मामले में, छोटे नमूने की एन्ट्रापी त्रुटि थोड़ी भी कम हो जाती है: k1 = 1.918 से k2 = 1.91 तक एंट्रॉपी गुणांक में मामूली कमी के साथ h1 = 0.46, h2 = 0.386।

बड़े और छोटे नमूनों के वितरण पैटर्न भिन्न होते हैं। जैसा कि विवरण से पता चलता है, 'doane' 'Sterges' स्कोर का एक उन्नत संस्करण है जो गैर-सामान्य वितरण के साथ डेटासेट के साथ बेहतर काम करता है। दोनों नमूनों में, एन्ट्रापी गुणांक दो के करीब है, और वितरण सामान्य के करीब है। इस हिस्टोग्राम पर एक छोटे नमूने में अतिरिक्त छलांग की उपस्थिति, पिछले एक की तुलना में, अतिरिक्त रूप से मूल्यांकनकर्ता 'एफडी' का सही विकल्प इंगित करता है।

हम मापदंडों के साथ सामान्य वितरण के लिए दो नए नमूने उत्पन्न करते हैं mu = 20, सिग्मा = 0.5 और आकार = 100 संबंध का उपयोग करते हुए:

 a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)])

विकसित विधि निम्नलिखित कार्यक्रम का उपयोग करके प्राप्त नमूने पर लागू होती है:

लिस्टिंग

 import matplotlib.pyplot as plt from numpy import* def diagram(a,m,n): z=histogram(a, bins=m) if type(m) is str:#      m=len(z[0]) y=z[0] d=z[1][1]-z[1][0]#   h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n)#   ke=h/std (a)#  return ke,h #a= list([round(random.normal(20,0.5),3) for x in arange(0,100,1)]) a=array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945,20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) c=['auto','fd','doane','scott','stone','rice','sturges','sqrt'] n=len(a) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] n1=len(b) print("     (n=100):%s"%round(std(a),3)) print("    (n=100):%s"%round(mean(a),3)) print("     (n=50):%s"%round(std(b),3)) print("   (n=50): %s"%round(mean(b),3)) u=[] for m in c: ke1,h1=diagram(a,m,n) ke2,h2=diagram(b,m,n1) u.append(abs(ke1-ke2)) print("ke1=%s,h1=%s,ke2=%s,h2=%s,dke=%s,m=%s"%(round(ke1,3),round(h1,3),round(ke2,3),round(h2,3),round(abs(ke1-ke2),3),m)) u1=min(u) c1=c[u.index(min(u))] u2=max(u) c2=c[u.index(max(u))] plt.title(' : %s \n    abs(ke1-ke2) :%s '%(c1,round(u1,3))) plt.hist(a,bins=str(c1)) plt.hist(b,bins=str(c1)) plt.grid() plt.show() plt.title('  : %s \n    abs(ke1-ke2):%s '%(c2,round(u2,3))) plt.hist(a,bins=str(c2)) plt.hist(b,bins=str(c2)) plt.grid() plt.show()

हमें मिलता है:
नमूने के लिए मानक विचलन (n = 100): 0.524
नमूने के लिए गणितीय अपेक्षा (n = 100): 19.992
नमूने के लिए मानक विचलन (n = 50): 0.462
नमूने की गणितीय अपेक्षा (n = 50): 20.002
ke1 = 1.979, h1 = 1.037, ke2 = 2.004, h2 = 0.926, dke = 0.025, m = ऑटो
ke1 = 1.979, h1 = 1.037, ke2 = 1.915, h2 = 0.885, dke = 0.064, m = fd
ke1 = 1.979, h1 = 1.037, ke2 = 1.804, h2 = 0.834, dke = 0.175, m = doane
ke1 = 1.943, h1 = 1.018, ke2 = 1.934, h2 = 0.894, dke = 0.009, m = स्कॉट
ke1 = 1.943, h1 = 1.018, ke2 = 1.804, h2 = 0.834, dke = 0.139, m = पत्थर
ke1 = 1.946, h1 = 1.02, ke2 = 1.804, h2 = 0.834, dke = 0.142, m = चावल
ke1 = 1.979, h1 = 1.037, ke2 = 2.004, h2 = 0.926, dke = 0.025, m = स्टर्ज
ke1 = 1.946, h1 = 1.02, ke2 = 1.804, h2 = 0.834, dke = 0.142, m = sqrt

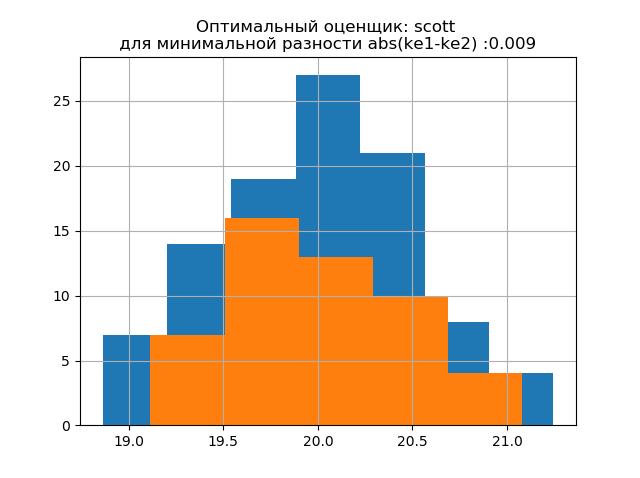
बड़े नमूने के वितरण का आकार छोटे नमूने के वितरण के आकार के समान है। विवरण के अनुसार, 'स्कॉट' एक कम विश्वसनीय मूल्यांकनकर्ता है जो डेटा की परिवर्तनशीलता और आकार को ध्यान में रखता है। इस मामले में, एक छोटे से नमूने की एन्ट्रापी त्रुटि थोड़ी भी कम हो जाती है: h1 = 1.018 और h2 = 0.894, k1 = 1.943 से k2 = 1.934 तक एन्ट्रापी गुणांक में मामूली कमी के साथ। । यह ध्यान दिया जाना चाहिए कि नए नमूने के लिए हमें पिछले उदाहरण के रूप में मापदंडों को बदलने की समान प्रवृत्ति मिली।

बड़े और छोटे नमूनों के वितरण पैटर्न भिन्न होते हैं। विवरण के अनुसार, 'डून' 'स्टर्गेस' अनुमान का एक उन्नत संस्करण है, जो गैर-सामान्य वितरण के साथ डेटा सेट के साथ अधिक सटीक रूप से काम करता है। दोनों नमूनों में, वितरण सामान्य है। पिछले एक की तुलना में इस हिस्टोग्राम पर एक छोटे से नमूने में अतिरिक्त छलांग की उपस्थिति अतिरिक्त रूप से 'स्कॉट' मूल्यांकनकर्ता की सही पसंद को इंगित करती है।

हिस्टोग्राम के तुलनात्मक विश्लेषण के लिए एंटी-अलियासिंग का उपयोग

बड़े और छोटे नमूनों पर निर्मित हिस्टोग्राम को चिकना करना आपको एक बड़े नमूने में निहित जानकारी को संरक्षित करने के दृष्टिकोण से उनकी पहचान को अधिक सटीक रूप से निर्धारित करने की अनुमति देता है। चौरसाई कार्यों के रूप में पिछले दो हिस्टोग्राम की कल्पना करें:

लिस्टिंग

 from numpy import* from scipy.interpolate import UnivariateSpline from matplotlib import pyplot as plt a =array([20.525, 20.923, 18.992, 20.784, 20.134, 19.547, 19.486, 19.346, 20.219, 20.55, 20.179,19.767, 19.846, 20.203, 19.744, 20.353, 19.948, 19.114, 19.046, 20.853, 19.344, 20.384, 19.945, 20.312, 19.162, 19.626, 18.995, 19.501, 20.276, 19.74, 18.862, 19.326, 20.889, 20.598, 19.974,20.158, 20.367, 19.649, 19.211, 19.911, 19.932, 20.14, 20.954, 19.673, 19.9, 20.206, 20.898, 20.239, 19.56,20.52, 19.317, 19.362, 20.629, 20.235, 20.272, 20.022, 20.473, 20.537, 19.743, 19.81, 20.159, 19.372, 19.998,19.607, 19.224, 19.508, 20.487, 20.147, 20.777, 20.263, 19.924, 20.049, 20.488, 19.731, 19.917, 19.343, 19.26,19.804, 20.192, 20.458, 20.133, 20.317, 20.105, 20.384, 21.245, 20.191, 19.607, 19.792, 20.009, 19.526, 20.37,19.742, 19.019, 19.651, 20.363, 21.08, 20.792, 19.946, 20.179, 19.8]) b=[a[i] for i in arange(0,len(a),1) if not i%2 == 0] plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="fd") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show() plt.title('    \n  abs(ke1-ke2)' ,size=12) z=histogram(a, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=100') z=histogram(b, bins="doane") x=z[1][:-1]+(z[1][1]-z[1][0])/2 f = UnivariateSpline(x, z[0], s=len(a)/2) plt.plot(x, f(x),linewidth=2,label='  n=50') plt.legend(loc='best') plt.grid() plt.show()

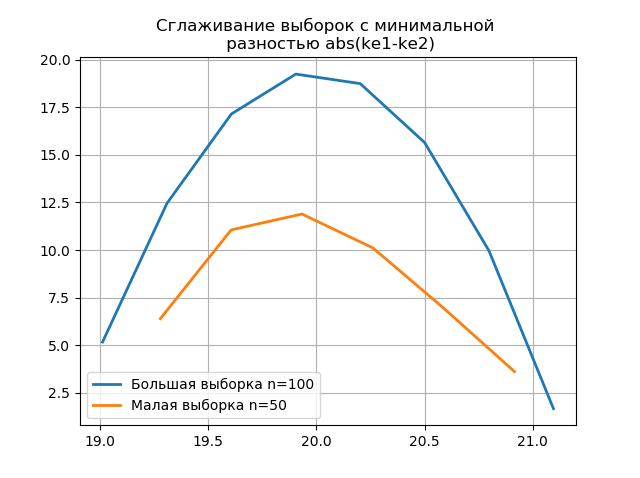
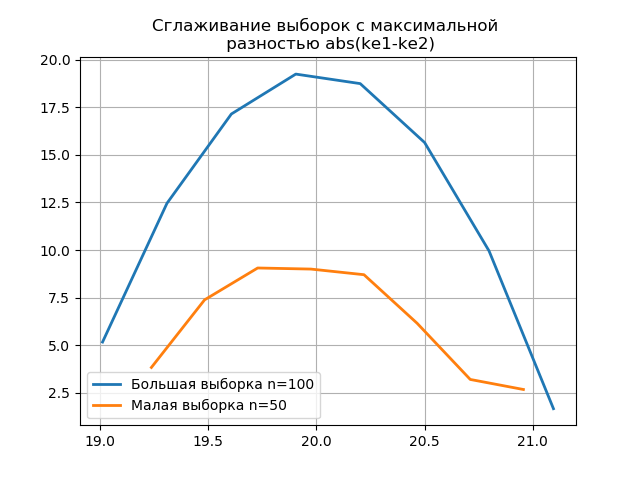
पिछले एक की तुलना में एक स्मूथ हिस्टोग्राम के ग्राफ पर एक छोटे से नमूने में अतिरिक्त छलांग की उपस्थिति अतिरिक्त रूप से स्कॉट एप्रेसर की सही पसंद को इंगित करती है।

निष्कर्ष

उत्पादन में छोटे नमूनों की श्रेणी में लेख में प्रस्तुत गणनाओं ने इसकी मात्रा में कमी के साथ नमूना की सूचना सामग्री को बनाए रखने के लिए एक मानदंड के रूप में एन्ट्रापी गुणांक का उपयोग करने की दक्षता की पुष्टि की। अंतर्निहित मूल्यांकनकर्ताओं के साथ numpy.histogram मॉड्यूल के नवीनतम संस्करण का उपयोग करने की तकनीक पर विचार किया जाता है - 'ऑटो', 'fd', 'doane', 'scott', 'stone', 'rice', 'Sterges', 'sqrt', जो अनुकूलन के लिए काफी हैं अंतराल अनुमानों पर प्रयोगात्मक डेटा का विश्लेषण।

संदर्भ:

1. तकनीकी अनुप्रयोगों के साथ हल्द ए गणितीय सांख्यिकी। - मॉस्को: पब्लिशिंग हाउस। लिट।, 1956
2. कलमीकोव वी.वी., एंटोनीक एफ.आई., ज़ेनकिन एन.वी.
अंतराल अनुमानों के लिए प्रायोगिक डेटा ग्रुपिंग कक्षाओं की इष्टतम संख्या का निर्धारण // दक्षिण साइबेरियाई वैज्ञानिक बुलेटिन। - 2014. - नहीं 3. पी। 56-58।
3. नोवित्स्की पी। वी। त्रुटि की एन्ट्रापी मूल्य की अवधारणा // मापने की तकनीक। - 1966। - संख्या 7.।एस। 11-14।
4.numpy.histogram - NumPy v1.16 मैनुअल

जानकारी के नुकसान के बिना प्रयोगात्मक डेटा के नमूना आकार में कमी

प्रायोगिक डेटा हिस्टोग्राम की समस्या क्या है

प्रयोगात्मक डेटा के हिस्टोग्राम की गुणवत्ता का मूल्यांकन करने के लिए मानदंडों का विकल्प

हिस्टोग्राम के तुलनात्मक विश्लेषण के लिए एंटी-अलियासिंग का उपयोग

निष्कर्ष

संदर्भ:

More articles: