परिचय

यह कैसे पता करें कि एक व्यक्ति समझ गया कि मठ क्या हैं? वह खुद आपको संचार के पहले 5 मिनट में इस बारे में बताएगा और निश्चित रूप से समझाने की कोशिश करेगा। वह इसके बारे में एक पाठ भी लिखेंगे और यदि संभव हो तो इसे कहीं प्रकाशित करें, ताकि हर कोई यह भी समझ सके कि मठ क्या हैं।

कार्यात्मक प्रोग्रामर के बीच, विशेष रूप से हास्केल पर, एक स्थानीय मेम का एक सा बन गया है। उन्हें अक्सर समझाने की कोशिश की जाती है, विशेष मामलों से शुरू होती है और तुरंत उपयोग का उदाहरण देती है। इस वजह से, श्रोता अवधारणा के मुख्य सार को समझ नहीं सकते हैं, और भिक्षुओं को काले जादू, अच्छी तरह से, या केवल विशुद्ध रूप से कार्यात्मक भाषाओं में साइड इफेक्ट को कुचलने का एक साधन बना रहेगा।

मैं पहले आपको श्रेणी सिद्धांत की मूल अवधारणाओं के बारे में बताऊंगा, और फिर एक व्यावहारिक दृष्टिकोण से हम एक सन्यासी की परिभाषा पर पहुंचेंगे और देखेंगे कि वास्तव में बहुत से प्रोग्रामर अपनी एक अभिव्यक्ति में इस शक्तिशाली अमूर्तता का उपयोग करते हैं।

मेरी प्रस्तुति काफी हद तक बार्टोज़ मिल्विक की पुस्तक, श्रेणी थ्योरी फॉर प्रोग्रामर्स पर आधारित है, जो ब्लॉग पोस्ट की एक श्रृंखला के रूप में बनाई गई थी, पीडीएफ में उपलब्ध है, और हाल ही में कागज में प्रकाशित हुई है।

हास्केल में उदाहरण दिए गए हैं, यह माना जाता है कि पाठक भाषा की वाक्य रचना और बुनियादी अवधारणाओं से परिचित है। उल्लिखित पुस्तक में C ++ में उदाहरण हैं, आप कोड की शुद्धता और समझ की तुलना कर सकते हैं।

श्रेणी

परिभाषा

श्रेणियां स्वयं बहुत सरल निर्माण हैं। एक श्रेणी वस्तुओं और उनके बीच आकारिकी का एक संग्रह है। आकृति विज्ञान को वस्तुओं को जोड़ने वाले अप्रत्यक्ष तीर के रूप में माना जा सकता है। सामान्य मामले में, वस्तुओं के सार के बारे में कुछ भी ज्ञात नहीं है। श्रेणी सिद्धांत वस्तुओं के साथ काम नहीं करता है, लेकिन आकृति विज्ञान के साथ, या बल्कि, उनकी रचना के साथ।

निम्नलिखित संकेतन का उपयोग किया जाता है:

• ओबी _सी - श्रेणी सी की वस्तुओं;
• होम _सी (ए, बी) - ए से बी तक आकारिकी;
• g and f आकार की संरचना है f और g।

एक श्रेणी को परिभाषित करने में, आकारिकी अतिरिक्त प्रतिबंधों के अधीन हैं:

1. एफ और जी की एक जोड़ी के लिए, अगर एफ ए से बी (एफ (होम (ए, बी)) से एक आकृतिवाद है, जी बी से सी (जी (होम (बी, सी)) से एक आकृतिवाद है, तो एक संरचना जी a मौजूद है f A से C तक का आकारिकी है (g ∈ f A होम (A, C))।
2. प्रत्येक ऑब्जेक्ट के लिए, एक पहचान आकारवाद आईडी _{ए A} होम (ए, ए) दिया जाता है।

दो महत्वपूर्ण गुण हैं जिन्हें किसी भी श्रेणी को संतुष्ट करना चाहिए (श्रेणी सिद्धांत के स्वयंसिद्ध):

1. रचना की संबद्धता: एच ∘ (जी = एफ) = (एच ivity जी); एफ;
2. पहचान आकृति विज्ञान के साथ रचना: यदि f the होम (ए, बी), तो एफ identity आईडी _ए = आईडी _बी । एफ = एफ।

श्रेणियों को बहुत आसानी से और स्वाभाविक रूप से निर्देशित रेखांकन के रूप में कल्पना की जाती है। सिद्धांत रूप में, यदि आवश्यक हो तो किसी भी उन्मुख ग्राफ को आकारिकी और समान आकार की रचनाओं को जोड़कर एक श्रेणी में बढ़ाया जा सकता है।

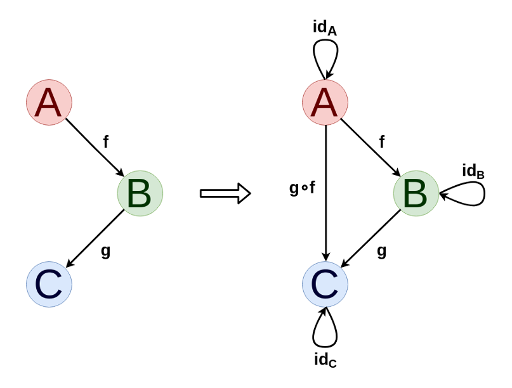
किसी भी श्रेणी के लिए, आप एक दोहरी श्रेणी को परिभाषित कर सकते हैं ( सी ^ऑप द्वारा निरूपित, जिसमें मूल श्रेणी के तीरों को मोड़कर आकार प्राप्त किया जाता है, और ऑब्जेक्ट समान होते हैं। यह हमें दोहरे विवरण और सिद्धांत बनाने की अनुमति देता है, जिनमें से तीर उल्टे होने पर सत्य नहीं बदलता है।

ऑब्जेक्ट और मॉर्फिज्म आवश्यक रूप से सेट (शास्त्रीय अर्थ में, सेट सिद्धांत से) नहीं बनाते हैं, इसलिए, सामान्य स्थिति में, वाक्यांश "वस्तुओं का वर्ग" का उपयोग किया जाता है। जिन श्रेणियों में वस्तुओं और आकारिकी के वर्ग अभी भी सेट हैं उन्हें छोटी श्रेणी कहा जाता है। आगे हम केवल उनके साथ काम करेंगे।

प्रकार और कार्य

, Haskell, — . , Int Bool — , Int -> Bool — .

id, :

id :: a -> a
id x = x

— , Haskell :

f :: a -> b
g :: b -> c
g . f :: a -> c
(g . f) x = g (f x)

, , — , Set. , — , : . bottom, _|_. , , , bottom. Haskell, , Hask. , Set. , , : Hom_C(A, B) ∈ C. , a -> b — Haskell.

.

Void, ( ). absurd, , , Void, :

absurd :: Void -> a

Unit, — , (). unit , :

unit :: a -> Unit
unit _ = ()

— Bool:

data Bool = True | False

, Void, Unit Bool.

Void , absurd, Bool, Unit. , Void, , .

Bool -> Unit , unit, . Unit -> Bool . (), True, False. , Unit Bool:

true, false :: a -> Bool
true _ = True
false _ = False

Bool Bool — , 4 ( n — 2²ⁿ): id, true false, , not:

not :: Bool -> Bool
not True = False
not False = True

, :

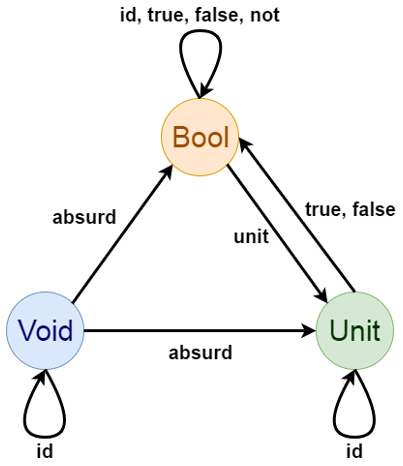
Haskell- .

— . , C D, F . -, C D. a — C, F a — D, . -, : f :: a -> b C F f :: F a -> F b D.

, " " :

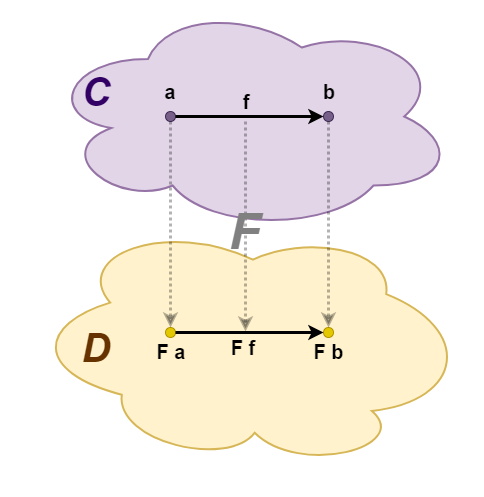
1. h = g ∘ f, F h = F g ∘ F f.
2. id_a — a, F id_a = id_{F a} — F a.

, "" : , , . , , () . , .

. , F :: C -> D G :: D -> E G . F :: C -> E. , , , , . Id_C, Id_D Id_E. , , .

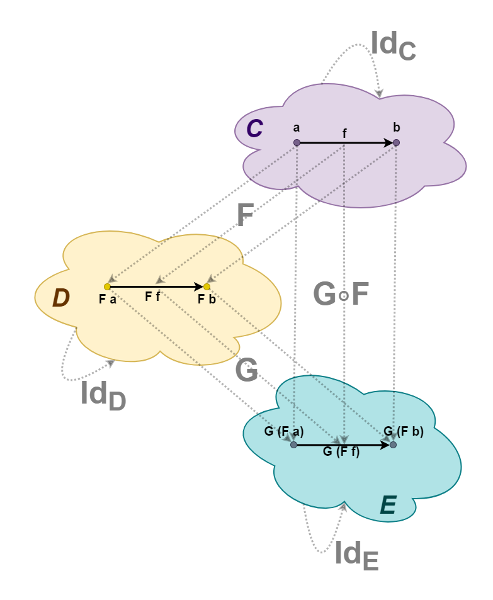
, , -, — (). , Cat ( ).

Haskell . , , - , .

Maybe , a Maybe a ( Maybe !):

data Maybe a = Nothing | Just a

, f :: a -> b F f :: Maybe a -> Maybe b. fmap. , ( ):

--          f                F f
--      /------\    /------------------\
fmap :: (a -> b) -> (Maybe a -> Maybe b)
fmap _ Nothing = Nothing
fmap f (Just x) = Just (f x)

, Maybe — . , , Functor. fmap, , ( — ):

class Functor f where
  fmap :: (a -> b) -> f a -> f b

— , , fmap . f a -> f b, , .

, , , .. , . : , - .

. , . , , — Haskell.

: upCase, , toWords, . toUpper words:

upCase :: String -> String
upCase = map toUpper

toWords :: String -> [String]
toWords = words

:

processString :: String -> [String]
processString = toWords . upCase

, . , processString "upCase toWords".

— , . -, , , -, , .

, a , .

newtype Writer a = Writer (a, String)

, Writer — , fmap:

instance Functor Writer where
  fmap f (Writer (x, s)) = Writer (f x, s)

upCase toWords , , "" Writer:

upCase :: String -> Writer String
upCase s = Writer (map toUpper s, "upCase ")

toWords :: String -> Writer [String]
toWords s = Writer (words s, "toWords ")

, , - . , b , , c c , :

compose :: (a -> Writer b) -> (b -> Writer c) -> (a -> Writer c)
compose f g = \x -> let Writer (y, s1) = f x
                        Writer (z, s2) = g y
                    in Writer (z, s1 ++ s2)

processString :

processString :: String -> [String]
processString = compose upCase toWords

. () a -> b a -> Writer b , a b. , .. a -> Writer a:

writerId :: a -> Writer a
writerId x = Writer (x, "")

, , Hask. , a b a -> b, a -> m b, .. "" - m. (embellished). m, Writer — .

C m. K, , C, .. Ob_K = Ob_C. a -> b K a -> m b C: Hom_K(a, b) = Hom_C(a, m b). , , K — C.

, , , . , m — . Haskell ( Hask):

class Monad m where
  --    
  (>=>)  :: (a -> m b) -> (b -> m c) -> (a -> m c)
  --  
  return :: a -> m a

>=>, "fish", : . , , — , , , . Writer — , compose — >=>, writerId — return.

>=> . , -. a, f, , , bind:

f >=> g = \a -> let mb = f a
                in (bind mb g)
  where
    bind :: m b -> (b -> m c) -> m c

bind b " " m , b m c. >=>. : m b -> (b -> m c) -> m c. , . "" Haskell >>=, bind, return:

class Monad m where
  (>>=)  :: m a -> (a -> m b) -> m b
  return :: a -> m a

, - b -> m c b, m b. , m, fmap, (a -> m b) -> m a -> m (m b). >>= m (m b) m b, "" , . join:

ma >>= g = join (fmap g ma)
  where
    join :: m (m a) -> m a

, Writer :

join :: Writer (Writer a) -> Writer a
join (Writer ((Writer (x, s2)), s1)) = Writer (x, s1 ++ s2)

Monad:

class Functor m => Monad m where
  join   :: m (m a) -> m a
  return :: a -> m a

, m . , fmap >>=:

fmap :: (a -> b) -> m a -> m b
fmap f ma = ma >>= (\a -> return (f a))

, "" .

(.. , ) .

(a -> [b]) -> (b -> [c]) -> (a -> [c]). :

(>=>) :: (a -> [b]) -> (b -> [c]) -> (a -> [c])
f >=> g = \x -> concat (map g (f x))

. a, , — f [b]. , b — g : map g (f x) :: [[c]]. , .

>>= :

(>>=) :: [a] -> (a -> [b]) -> [b]
xs >>= f = concat (map f xs)

return :: a -> [a]. :

return :: a -> [a]
return x = [x]

Monad:

instance Monad [] where
  xs >>= f = concat (map f xs)
  return x = [x]

, . , , . , — , ..

, , - .

, , Maybe. Just, — Nothing. , , :

(>=>) :: (a -> Maybe b) -> (b -> Maybe c) -> (a -> Maybe c)
f >=> g = \x -> case f x of
                  Just y  -> g y
                  Nothing -> Nothing

Monad Maybe:

instance Monad Maybe where
  (Just x) >>= f = f x
  Nothing  >>= f = Nothing
  return x = Just x

, . , - , , - . Either String a, : , . :

data Either a b = Left a | Right b

, . . :

type WithException a = Either String a

Maybe:

(>=>) :: (a -> WithException b) -> (b -> WithException c) -> (a -> WithException c)
f >=> g = \x -> case f x of
                  Right y -> g y
                  err     -> err

Monad :

instance Monad WithException where
  (Right x) >>= f = f x
  err >>= f = err
  return x = Right x

, , write-only , . a -> b , , . , , ( , ):

a -> s -> (b, s)

:

newtype State s a = State (s -> (a, s))

s , State s . runState:

runState :: State s a -> s -> (a, s)
runState (State f) s = f s

Functor:

instance Functor (State s) where
  fmap f state = State st'
    where
     st' prevState = let (a, newState) = runState state prevState
                     in (f a, newState)

, a b, , a -> State s b, State s — . , :

(>=>) :: (a -> State s b) -> (b -> State s c) -> (a -> State s c)
f >=> g = \x -> State (\s -> let (y, s') = runState (f x) s
                             in runState (g y) s')

Monad. , return, , -:

instance Monad (State s) where
  stateA >>= f = State (\s -> let (a, s') = runState stateA s
                              in runState (f a) s')
  return a = State (\s -> (a, s))

, . , Unit s , Unit -> State s s:

get :: Unit -> State s s
get _ = State (\s -> (s, s))

, Unit . , .

, , . , , , s Unit, s -> State s Unit:

put :: s -> State s Unit
put s = State (\_ -> ((), s))

, , /. , " " RealWorld, . RealWorld - , (, ). :

type IO a = State RealWorld a

IO — , Haskell, "". , . , , , -, .