👩‍🔧 🏞️ ☹️ तंत्रिका क्वांटम स्टेट्स - एक तंत्रिका नेटवर्क द्वारा एक तरंग समारोह का प्रतिनिधित्व 🌹 🕵🏽 👅

इस लेख में, हम विशेष रूप से क्वांटम यांत्रिकी की दो जटिल समस्याओं को हल करने के लिए सामान्य रूप से और सीमित बोल्ट्जमन मशीनों में तंत्रिका नेटवर्क के असामान्य अनुप्रयोग पर विचार करेंगे - जमीनी राज्य ऊर्जा का पता लगाना और कई-निकाय प्रणाली की तरंग फ़ंक्शन का अनुमान लगाना।

हम यह कह सकते हैं कि यह एक लेख [2] की एक नि: शुल्क और सरल रीटेलिंग है, जिसे 2017 में विज्ञान और कुछ बाद के कार्यों में प्रकाशित किया गया है। मुझे रूसी में इस काम के लोकप्रिय वैज्ञानिक प्रसार नहीं मिले (और केवल यह अंग्रेजी संस्करणों में से एक है), हालांकि यह मुझे बहुत दिलचस्प लगा।

क्वांटम यांत्रिकी और गहन शिक्षा से न्यूनतम आवश्यक अवधारणाएं

मैं तुरंत ध्यान देना चाहता हूं कि ये परिभाषाएं बहुत सरल हैं । मैं उन्हें उन लोगों के लिए लाता हूं जिनके लिए वर्णित समस्या एक अंधेरे जंगल है।

एक राज्य केवल भौतिक मात्रा का एक सेट है जो एक प्रणाली का वर्णन करता है। उदाहरण के लिए, अंतरिक्ष में उड़ने वाले इलेक्ट्रॉन के लिए यह उसका निर्देशांक और गति होगा, और क्रिस्टल जाली के लिए यह अपने नोड्स में स्थित परमाणुओं के एक प्रकार का एक समूह होगा।

सिस्टम की तरंग प्रणाली प्रणाली की स्थिति का एक जटिल कार्य है। एक निश्चित ब्लैक बॉक्स जो एक इनपुट लेता है, उदाहरण के लिए, स्पिन का एक सेट, लेकिन एक जटिल संख्या देता है। हमारे लिए महत्वपूर्ण तरंग समारोह की मुख्य संपत्ति यह है कि इसका वर्ग इस राज्य की संभावना के बराबर है:

P s i (s) P s i (s)^{*} = P (s)

$\ Psi (s) \ Psi (s) ^ * = P (s)$

यह तर्कसंगत है कि लहर फ़ंक्शन के वर्ग को एकता के लिए सामान्यीकृत किया जाना चाहिए (और यह भी महत्वपूर्ण समस्याओं में से एक है)।

हिल्बर्ट स्पेस - हमारे मामले में, ऐसी परिभाषा पर्याप्त है - सिस्टम के सभी संभावित राज्यों का स्थान। उदाहरण के लिए, 40 स्पिंस की एक प्रणाली के लिए जो मान +1 या -1 ले सकते हैं, हिल्बर्ट स्पेस सभी है

2^{40}

$2 ^ {40}$ संभव शर्तें। निर्देशांक के लिए जो मान ले सकते हैं

[- i n f t y, + i n f t y]

$[- \ infty, + \ infty]$ हिल्बर्ट अंतरिक्ष का आयाम अनंत है। यह किसी भी वास्तविक सिस्टम के लिए हिल्बर्ट स्थान का एक बड़ा आयाम है जो मुख्य समस्या है जो समीकरणों को विश्लेषणात्मक रूप से हल करने की अनुमति नहीं देता है: इस प्रक्रिया में पूरे हिल्बर्ट स्थान पर अभिन्न / योग होंगे जिनकी गणना "हेड-ऑन" नहीं की जा सकती है। एक जिज्ञासु तथ्य: ब्रह्मांड के पूरे जीवन के लिए आप हिल्बर्ट अंतरिक्ष में शामिल सभी संभावित राज्यों के एक छोटे से हिस्से से मिल सकते हैं। यह बहुत अच्छी तरह से Tensor Networks [1] के बारे में एक लेख से एक चित्र द्वारा चित्रित किया गया है, जिसमें योजनाबद्ध रूप से पूरे हिल्बर्ट स्थान और उन राज्यों को दर्शाया गया है जो अंतरिक्ष की जटिलता (निकायों, कणों, Spins, आदि) की विशेषता से एक बहुपद के बाद मिल सकते हैं।

एक सीमित बोल्ट्जमन मशीन - यदि समझाने में मुश्किल है, तो यह एक अप्रत्यक्ष चित्रमय संभाव्य मॉडल है, जिसकी सीमा एक परत के नोड्स से एक परत के नोड्स की संभावनाओं की सशर्त स्वतंत्रता है। यदि एक सरल तरीके से, तो यह एक तंत्रिका नेटवर्क है जिसमें एक इनपुट और एक छिपी हुई परत है। छिपी हुई परत में न्यूरॉन्स के आउटपुट का मान 0 या 1. हो सकता है। सामान्य तंत्रिका नेटवर्क से अंतर यह है कि छिपी हुई परत के न्यूरॉन्स के आउटपुट यादृच्छिक चर हैं जो सक्रियण फ़ंक्शन के मान के बराबर संभावना के साथ चयनित हैं:

P_{i} (1) = s i g m a (b_{i} + s u m_{j} W_{i j} s_{j})

$P_i (1) = \ sigma (b_i + \ sum_jW_ {ij} s_j)$

जहाँ

_{स} ि ग ् म ा

$\ _ सिग्मा$ - सिग्माइड एक्टिवेशन फंक्शन ,

b_{i}

$b_i$ - मैं-वें न्यूरॉन के लिए ऑफसेट,

ड ब ् ल ् य ू

$डब्ल्यू$ - तंत्रिका नेटवर्क का वजन,

s_{j}

$s_j$ - दृश्य परत। सीमित बोल्ट्ज़मन मशीनें तथाकथित "ऊर्जा मॉडल" से संबंधित हैं, क्योंकि हम इस मशीन की ऊर्जा का उपयोग करके किसी मशीन के किसी विशेष राज्य की संभावना व्यक्त कर सकते हैं:

E (v, h) = - a^{T} v - b^{T} h - v^{T} W h

$E (v, h) = -a ^ Tv - b ^ Th - v ^ TWh$

जहाँ v और h दृश्यमान और छिपी हुई परतें हैं, a और b दृश्यमान और छिपी हुई परतों के विस्थापन हैं, W भार हैं। तब राज्य की संभावना फार्म में प्रतिनिधित्व करने योग्य है:

P (v, h) = f r a c 1 Z e^{- E (v, h)}

$P (v, h) = \ frac {1} {Z} e ^ {- E (v, h)}$

जहाँ Z सामान्यीकरण शब्द है, जिसे सांख्यिकीय योग भी कहा जाता है (यह आवश्यक है ताकि कुल संभावना एकता के बराबर हो)।

परिचय

आज, गहरी सीखने के विशेषज्ञों के बीच एक राय है जो सीमित है
बोल्ट्ज़मन मशीनें (इसके बाद - ओएमबी) एक पुरानी अवधारणा है जो वास्तविक कार्यों में व्यावहारिक रूप से लागू नहीं होती है। हालांकि, 2017 में, विज्ञान में एक लेख [2] सामने आया जिसमें क्वांटम यांत्रिकी की समस्याओं के लिए ओएमबी का बहुत कुशल उपयोग दिखाया गया था।

लेखकों ने दो महत्वपूर्ण तथ्यों पर गौर किया, जो स्पष्ट प्रतीत हो सकते हैं, लेकिन वे पहले कभी किसी के साथ नहीं हुए थे:

ओएमबी एक तंत्रिका नेटवर्क है, जो त्सेंको के सार्वभौमिक प्रमेय के अनुसार , सैद्धांतिक रूप से किसी भी कार्य को मनमाने ढंग से उच्च सटीकता के साथ कर सकता है (अभी भी बहुत सारे प्रतिबंध हैं, लेकिन आप उन्हें छोड़ सकते हैं)।
ओएमबी एक ऐसी प्रणाली है जिसकी प्रत्येक राज्य की संभावना इनपुट (दृश्य परत), वजन और तंत्रिका नेटवर्क के विस्थापन का एक कार्य है।

अच्छी तरह से और लेखकों ने कहा: हमारे सिस्टम को पूरी तरह से तरंग फ़ंक्शन द्वारा वर्णित किया जाना चाहिए, जो कि ओएमबी ऊर्जा की जड़ है, और ओएमबी इनपुट हमारे सिस्टम की स्थिति (निर्देशांक, स्पिन, आदि) की विशेषताएं हैं:

\ Psi (s) = \ frac {1} {Z} \ sqrt {e ^ {E (s, h)} $

$\ Psi (s) = \ frac {1} {Z} \ sqrt {e ^ {E (s, h)} $$

जहां राज्य की विशेषताएं हैं (उदाहरण के लिए, स्पिन), एच ओएमबी की छिपी हुई परत के आउटपुट हैं, ई ओएमबी की ऊर्जा है, जेड सामान्यीकरण स्थिरांक (सांख्यिकीय योग) है।

यही है, विज्ञान में लेख तैयार है, फिर केवल कुछ छोटे विवरण शेष हैं। उदाहरण के लिए, हिल्बर्ट स्पेस के विशाल आकार के कारण गैर-कम्प्यूटेबल विभाजन फ़ंक्शन की समस्या को हल करना आवश्यक है। और Tsybenko की प्रमेय हमें बताती है कि एक तंत्रिका नेटवर्क किसी भी फ़ंक्शन को अनुमानित कर सकता है, लेकिन यह बिल्कुल नहीं कहता है कि इसके लिए नेटवर्क वेट और ऑफ़सेट का एक उपयुक्त सेट कैसे खोजा जाए। खैर, और हमेशा की तरह, मज़ा यहाँ शुरू होता है।

मॉडल प्रशिक्षण

अब मूल दृष्टिकोण के कुछ संशोधन हैं, लेकिन मैं केवल मूल लेख [2] से दृष्टिकोण पर विचार करूंगा।

कार्य

हमारे मामले में, प्रशिक्षण कार्य निम्नानुसार होगा: लहर फ़ंक्शन का एक अनुमान लगाने के लिए जो राज्य को न्यूनतम ऊर्जा के साथ सबसे अधिक संभावित बना देगा। यह सहज रूप से स्पष्ट है: तरंग फ़ंक्शन हमें एक राज्य की संभावना देता है, हैमिल्टनियन (ऊर्जा ऑपरेटर, या यहां तक कि सरल, ऊर्जा - इस लेख के ढांचे में, यह समझ पर्याप्त है) तरंग कार्य के लिए ऊर्जा है। सब कुछ सरल है।

वास्तव में, हम एक और मात्रा, तथाकथित स्थानीय ऊर्जा को अनुकूलित करने का प्रयास करेंगे, जो हमेशा जमीन की ऊर्जा की तुलना में अधिक या बराबर होती है:

$display$ यहां $\ _ सिग्मा$ हमारी हालत है $\ _ 'सिग्मा'$ - हिल्बर्ट अंतरिक्ष के सभी संभावित राज्यों (वास्तव में हम एक अधिक अनुमानित मूल्य पर विचार करेंगे), $H _ {\ _ sigma \ sigma '}$ हैमिल्टनियन का मैट्रिक्स तत्व है। भारी हामिल्टनियन पर निर्भर है, उदाहरण के लिए, ईज़िंग मॉडल के लिए, यह सिर्फ है $f (\ sigma)$ अगर $\ _ सिग्मा = \ सिग्मा '$ , और $-कॉस्ट$ अन्य सभी मामलों में। अब यहाँ मत रुकना; यह महत्वपूर्ण है कि इन तत्वों को विभिन्न लोकप्रिय हैमिल्टन के लिए पाया जा सकता है।

अनुकूलन प्रक्रिया

नमूना

मूल लेख से दृष्टिकोण का एक महत्वपूर्ण हिस्सा नमूना प्रक्रिया था। मेट्रोपोलिस-हेस्टिंग्स एल्गोरिथम का संशोधित रूपांतर किया गया था। नीचे पंक्ति है:

हम एक यादृच्छिक स्थिति से शुरू करते हैं।
हम एक यादृच्छिक रूप से चयनित स्पिन के चिन्ह को विपरीत में बदलते हैं (निर्देशांक के लिए अन्य संशोधन हैं, लेकिन वे भी मौजूद हैं)।
के बराबर संभावना के साथ $P (\ sigma '| \ sigma) = \ Big | {\ frac {\ _ psi (\ sigma')}} {\ psi (\ sigma)} \ Big | ^ 2$ , एक नए राज्य में ले जाएँ।
एन बार दोहराएँ।

नतीजतन, हम वितरण के अनुसार चयनित यादृच्छिक राज्यों का एक सेट प्राप्त करते हैं जो हमारी लहर फ़ंक्शन हमें देता है। आप प्रत्येक राज्य में ऊर्जा मूल्यों और ऊर्जा की गणितीय अपेक्षा की गणना कर सकते हैं

m a t h b b E (E_{l o c})

$\ mathbb {E} (E_ {loc})$ ।

यह दिखाया जा सकता है कि ऊर्जा ढाल का अनुमान (अधिक सटीक रूप से, हैमिल्टन का अपेक्षित मूल्य) इसके बराबर है:

G_{k} (x) = 2 * (E_{l o c} (x) - m a t h b b E (E_{l o c})) * D_{k}^{*} (x)

$G_k (x) = 2 * (E_ {loc} (x) - \ mathbb {E} (E_ {loc})) * D ^ * _ k (x)$

निष्कर्ष

यह 2017 में क्वांटम साइंस और क्वांटम टेक्नोलॉजी पर एडवांस्ड स्कूल के लिए जी कार्लो द्वारा दिए गए एक व्याख्यान से है। Youtube पर प्रविष्टियाँ हैं।

निरूपित:

D_{k}^{*} (x) = f r a c आ ं श ि क_{p_{k}} P s i (x) P s i (x)

$D ^ * _ k (x) = \ frac {\ आंशिक_ {p_k} \ Psi (x)} {\ Psi (x)}$

तब:

आ ं श ि क_{p_{k}} m a t h b b E (ए च) =

$\ आंशिक_ {p_k} \ mathbb {E} (एच) =$

आ ं श ि क f r a c_{s} u m_{x x^{'}} p s i^{*} (x) H_{x x^{'}} p s i (x^{'}) s u m_{x} | p s i (x) |^{2} =

$\ आंशिक \ frac {\ _ sum_ {xx '} \ psi ^ * (x) H_ {xx'} \ psi (x ')} {\ sum_x | \ psi (x) | ^ 2} =$

f r a c_{s} u m_{x x^{'}} p s i^{*} (x) H_{x x^{'}} D_{k} (x^{'}) p s i (x^{'}) s u m_{x} | p s i (x)^{2} + f r a c s u m_{x x^{'}} P s i^{*} (x) D_{k}^{*} (x) H_{x x^{'}} P s i (x^{'}) s u m_{x} | p s i (x) |^{2} -

$\ frac {\ _ sum_ {xx '} \ psi ^ * (x) H_ {xx'} D_k (x ') \ psi (x')} {\ sum_x | \ psi (x) ^ 2} + \ frac {sum_ {xx '} \ Psi ^ * (x) D_k ^ * (x) H_ {xx'} \ Psi (x ')} {\ sum_x | \ psi (x) | ^ 2} -$

\ frac {\ _ sum_ {xx '} \ psi ^ * (x) H_ {xx'} \ psi (x ')} {\ sum_x | \ psi (x) | ^ 2} \ frac {sum_x_ \ psi (x) | ^ 2 (D_k (x) - D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2} =

$\ frac {\ _ sum_ {xx '} \ psi ^ * (x) H_ {xx'} \ psi (x ')} {\ sum_x | \ psi (x) | ^ 2} \ frac {sum_x_ \ psi (x) | ^ 2 (D_k (x) - D ^ * _ k (x))} {\ sum_x | \ Psi (x) | ^ 2} =$

f r a c_{s} u m_{x x^{'}} f r a c_{p} s i * * (x) p s i^{*} (x^{'}) H_{x x^{'}} D_{k} (x^{'}) | p s i (x))^{|} 2 + s u m_{x x^{'}} | P s i (x) |^{2} H_{x x^{'}} D_{k}^{*} (x^{'}) f r a c_{p} s i (x^{'})_{p} s i (x) s u m_{x} | P s i (x) |^{2} -

$\ frac {\ _ sum_ {xx '} \ frac {\ _ psi * * (x)} {\ psi ^ * (x')} H_ {xx '} D_k (x') | \ psi (x)) ^ | 2 + \ sum_ {xx '} | \ Psi (x) | ^ 2H_ {xx'} D ^ * _ k (x ') \ frac {\ _ psi (x')} {\ _ psi (x)}} {\ sum_x | \ Psi (x) | ^ 2} -$

m a t h b b E (H) f r a c s u m_{x} | P s i (x) |^{2} (D_{k} (x) + D_{k}^{*} (x)) s u m_{x} | P s i (x)^{2} |_{ल} ग भ ग

$\ mathbb {E} (H) \ frac {\ sum_x | \ Psi (x) | ^ 2 (D_k (x) + D ^ * _ k (x))} {\ sum_x | \ Psi (x) ^ 2 | } \ _ लगभग$

m a t h b b E (E_{l o c} D_{k}^{*}) - m a t h b b E (E_{l o c}) m a t h b b E (D_{k}^{*}) + C

$\ mathbb {E} (E_ {loc} D ^ * _ k) - \ mathbb {E} (E_ {loc}) \ mathbb {E} (D ^ * _ k) + C$

तब हम सिर्फ अनुकूलन समस्या का समाधान करते हैं:

हम अपने ओएमबी से राज्यों का नमूना लेते हैं।
हम प्रत्येक राज्य की ऊर्जा की गणना करते हैं।
ढाल का अनुमान लगाएं।
हम ओएमबी के वजन को अपडेट करते हैं।

परिणामस्वरूप, ऊर्जा प्रवणता शून्य हो जाती है, ऊर्जा मूल्य कम हो जाता है, जैसा कि मेट्रोपोलिस-हेस्टिंग्स प्रक्रिया में अद्वितीय नए राज्यों की संख्या है, क्योंकि सच्ची लहर फ़ंक्शन से नमूना लेने से हमें लगभग हमेशा जमीनी अवस्था मिलेगी। सहज रूप से, यह तर्कसंगत लगता है।

मूल काम में, छोटे सिस्टम के लिए, जमीन राज्य ऊर्जा के मूल्यों को प्राप्त किया गया था, विश्लेषणात्मक रूप से प्राप्त सटीक मूल्यों के बहुत करीब। जमीनी राज्य की ऊर्जा को खोजने के लिए अच्छी तरह से ज्ञात दृष्टिकोण के साथ एक तुलना की गई थी, और एनक्यूएस ने जीत हासिल की, विशेष रूप से ज्ञात विधियों की तुलना में एनक्यूएस की अपेक्षाकृत कम कम्प्यूटेशनल जटिलता पर विचार किया।

NetKet - "आविष्कारकों" दृष्टिकोण से एक पुस्तकालय

मूल लेख के लेखकों में से एक [2] ने अपनी टीम के साथ उत्कृष्ट नेटकेट लाइब्रेरी [3] विकसित की, जिसमें बहुत अच्छी तरह से अनुकूलित (मेरी राय में) सी-कर्नेल, साथ ही पायथन एपीआई भी शामिल है, जो उच्च-स्तरीय गर्भपात के साथ काम करता है।

पुस्तकालय को पाइप के माध्यम से स्थापित किया जा सकता है। विंडोज 10 उपयोगकर्ताओं को विंडोज के लिए लिनक्स सबसिस्टम का उपयोग करना होगा।

आइए लाइब्रेरी के साथ काम करने पर विचार करें + मान / -1 / 2 लेने वाली 40 स्पिनों की एक श्रृंखला के उदाहरण के रूप में। हम हाइजेनबर्ग मॉडल पर विचार करेंगे, जो पड़ोसी बातचीत को ध्यान में रखता है।

NetKet के पास उत्कृष्ट प्रलेखन है जो आपको जल्दी से यह पता लगाने की अनुमति देता है कि क्या और कैसे करना है। कई बिल्ट-इन मॉडल (बैक, बोसॉन, ईज़िंग, हाइजेनबर्ग मॉडल, आदि) हैं, और मॉडल को पूरी तरह से वर्णन करने की क्षमता है।

गणना विवरण

सभी मॉडलों को रेखांकन में प्रस्तुत किया गया है। हमारी श्रृंखला के लिए, एक आयाम और आवधिक सीमा शर्तों के साथ निर्मित हाइपरक्यूब मॉडल उपयुक्त है:

import netket as nk graph = nk.graph.Hypercube(length=40, n_dim=1, pbc=True)

हिल्बर्ट स्पेस का वर्णन

हमारी हिल्बर्ट स्पेस बहुत ही सरल है - सभी स्पिन या तो +1 / 2 या -1/2 मान ले सकते हैं। इस मामले के लिए, स्पिन के लिए निर्मित मॉडल उपयुक्त है:

 hilbert = nk.hilbert.Spin(graph=graph, s=0.5)

हैमिल्टन का वर्णन

जैसा कि मैंने पहले ही लिखा है, हमारे मामले में हैमिल्टन हीजेनबर्ग हैमिल्टन है जिसके लिए एक अंतर्निहित ऑपरेटर है:

 hamiltonian = nk.operator.Heisenberg(hilbert=hilbert)

आरबीएम का विवरण

नेटकेट में, आप स्पिन के लिए एक तैयार किए गए आरबीएम कार्यान्वयन का उपयोग कर सकते हैं - यह सिर्फ हमारा मामला है। लेकिन सामान्य तौर पर कई कारें हैं, आप अलग-अलग कोशिश कर सकते हैं।

 nk.machine.RbmSpin(hilbert=hilbert, alpha=4) machine.init_random_parameters(seed=42, sigma=0.01)

यहाँ अल्फ़ा छिपी हुई परत में न्यूरॉन्स का घनत्व है। दृश्यमान और अल्फा 4 के 40 न्यूरॉन्स के लिए, उनमें से 160 होंगे। संख्या द्वारा सीधे संकेत देने का एक और तरीका है। दूसरी कमांड वेट को बेतरतीब ढंग से शुरू करती है

ए न (0, स ि ग ् म ा)

$एन (0, \ सिग्मा)$ । हमारे मामले में, सिग्मा 0.01 है।

semler

एक नमूना एक वस्तु है जो हमारे वितरण से एक नमूना द्वारा हमें लौटा दी जाएगी, जो हिल्बर्ट अंतरिक्ष पर लहर फ़ंक्शन द्वारा दी गई है। हम ऊपर वर्णित मेट्रोपोलिस-हेस्टिंग्स एल्गोरिथम का उपयोग करेंगे, हमारे कार्य के लिए संशोधित:

 sampler = nk.sampler.MetropolisExchangePt( machine=machine, graph=graph, d_max=1, n_replicas=12 )

सटीक होने के लिए, नमूना जो मैंने ऊपर वर्णित किया है उसकी तुलना में एक पेचीदा एल्गोरिथ्म है। यहां हम एक साथ अगले बिंदु का चयन करने के लिए समानांतर में 12 विकल्पों की जांच करते हैं। लेकिन सिद्धांत, सामान्य रूप से, समान है।

अनुकूलक

यह ऑप्टिमाइज़र का वर्णन करता है जिसका उपयोग मॉडल भार को अपडेट करने के लिए किया जाएगा। उन क्षेत्रों में तंत्रिका नेटवर्क के साथ काम करने वाले व्यक्तिगत अनुभव के अनुसार जो उनके लिए अधिक "परिचित" हैं, सबसे अच्छा और सबसे विश्वसनीय विकल्प एक पल के साथ अच्छा पुराना स्टोकेस्टिक ढाल वंश है (अच्छी तरह से यहां वर्णित):

 opt = nk.optimizer.Momentum(learning_rate=1e-2, beta=0.9)

ट्रेनिंग

NetKet ने एक शिक्षक (हमारा मामला) के बिना और एक शिक्षक के साथ प्रशिक्षण दिया है (उदाहरण के लिए, तथाकथित "क्वांटम टोमोग्राफी", लेकिन यह एक अलग लेख का विषय है)। हम बस "शिक्षकों" का वर्णन करते हैं, और यह है:

 vc = nk.variational.Vmc( hamiltonian=hamiltonian, sampler=sampler, optimizer=opt, n_samples=1000, use_iterative=True )

परिवर्तनशील मोंटे कार्लो इंगित करता है कि हम उस फ़ंक्शन के ग्रेडिएंट का मूल्यांकन करते हैं जिसका हम अनुकूलन कर रहे हैं। n_smaples हमारे वितरण से नमूने का आकार है जो नमूना देता है।

परिणाम

हम मॉडल निम्नानुसार चलाएंगे:

 vc.run(output_prefix=output, n_iter=1000, save_params_every=10)

लाइब्रेरी OpenMPI का उपयोग करके बनाई गई है, और स्क्रिप्ट को इस तरह चलाना होगा: mpirun -n 12 python Main.py (12 कोर की संख्या है)।

मुझे मिले परिणाम इस प्रकार हैं:

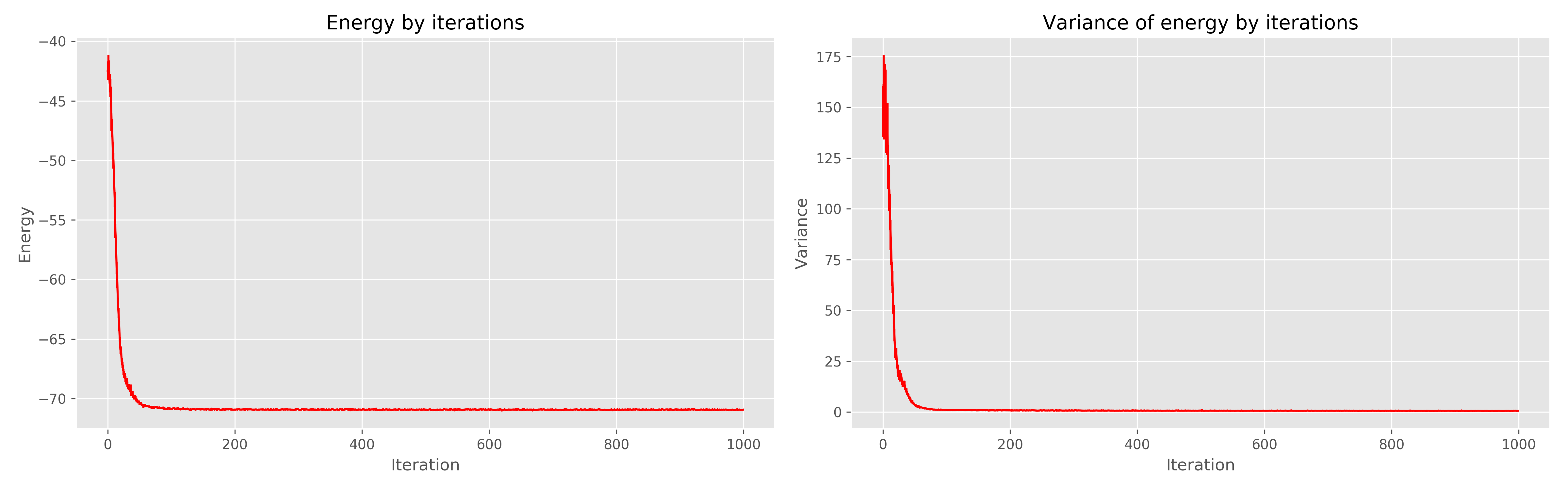
बाईं ओर सीखने के युग से ऊर्जा का एक ग्राफ है, दाईं ओर सीखने के युग से ऊर्जा का फैलाव है।
यह देखा जा सकता है कि 1000 युग स्पष्ट रूप से निरर्थक हैं, 300 पर्याप्त होगा। सामान्य तौर पर, यह बहुत अच्छा काम करता है, जल्दी से परिवर्तित होता है।

साहित्य

ओआरयूएस आर। टेंसर नेटवर्क के लिए एक व्यावहारिक परिचय: मैट्रिक्स उत्पाद राज्यों और अनुमानित उलझाव जोड़ी राज्यों // भौतिकी के इतिहास। - 2014 ।-- टी। 349. - एस। 117-158।
कार्लो जी, ट्रॉयर एम। कृत्रिम तंत्रिका नेटवर्क // विज्ञान के साथ क्वांटम कई-शरीर की समस्या का समाधान। - 2017. - टी। 355. - नहीं। 6325. - एस 602-606।
www.netket.org

तंत्रिका क्वांटम स्टेट्स - एक तंत्रिका नेटवर्क द्वारा एक तरंग समारोह का प्रतिनिधित्व