क्वांटम रसायन विज्ञान के संदर्भ में मून उत्प्रेरक। भाग II: इलेक्ट्रॉनिक बनाम म्यूऑन रासायनिक बंधन

Mnogabukaff कि क्वांटम रसायन विज्ञान मुओन कटैलिसीस के सिद्धांत के बारे में सोचता है: कैसे मुआन वांछित प्लाज्मा के तापमान को कम करता है। दो भागों में (पहला भाग यहाँ पढ़ा जा सकता है )।

दूसरे भाग का सार सरल है: म्यूऑन इलेक्ट्रॉन से भारी है, इसलिए यह एक मजबूत रासायनिक बंधन और नाभिक के करीब पहुंच प्रदान करता है, जिससे थर्मोन्यूक्लियर प्रतिक्रिया को प्रज्वलित करने के लिए आवश्यक प्लाज्मा तापमान कम हो जाता है।

लेकिन जो लोग सूत्र, रेखांकन को देखना चाहते हैं, और क्वांटम रसायन के वैचारिक सार को देखते हैं जैसा कि सरलतम (अर्ध) अणुओं पर लागू होता है, बिल्ली के नीचे स्वागत है।

परिचय

पहले भाग में ( यहां देखें) हमने एक हाइड्रोजन परमाणु के बीच अंतर की जांच की $$$\ mathrm {H} ^ \ cdot = \ mathrm {p ^ + e ^ -}$ अपने भारी म्यूऑन समकक्ष से $$$\ mathrm {p} ^ + \ mu ^ -$ : दूसरे मामले में, म्यूऑन को अधिक मजबूती से बांधा जाएगा, और यह प्रोटॉन से अधिक दूरी पर बैठेगा। उसी समय, हमने कुछ महत्वपूर्ण चीजों की जांच की, जिनकी हमें यहां आवश्यकता होगी (कक्षाओं के प्रकार और इकाइयों की परमाणु प्रणाली)।

दूसरे भाग (यानी, यहां) में हम यह समझने की कोशिश करेंगे कि थर्मोन्यूक्लियर प्रतिक्रिया को प्रज्वलित करने के लिए आवश्यक प्लाज्मा तापमान क्यों और कैसे घट जाएगा। हमारी रूचि की प्रतिक्रियाएँ:

$$

$$\ mathrm {{} ^ nH + {} ^ m H \ rightarrow} \ \ text {नई कर्नेल + ऊर्जा}$$

जहां n, m = 1,2,3 क्रमशः प्रोटॉन, ड्यूटेरियम और ट्रिटियम के अनुरूप हैं। स्वाभाविक रूप से, इन नाभिकों पर एक सकारात्मक चार्ज होता है, इसलिए यदि आप उन्हें करीब लाने की कोशिश करते हैं, तो वे कोलोम्ब कानून ( पिछले भाग को देखें) के अनुसार पीछे हटाना शुरू कर देंगे, और यह बहुत ही बाधा है जो थर्मामीटरिक संलयन प्रतिक्रियाओं की शुरुआत को रोकता है। वैसे, परमाणु क्षय प्रतिक्रियाओं के मामले में, इस प्रतिकर्षण की विपरीत भूमिका होती है, क्योंकि आम नाभिक से अलग होने के बाद, टुकड़े, एक दूसरे से repelling, अतिरिक्त गतिज ऊर्जा प्राप्त करते हैं, और यह वह ऊर्जा है जो परमाणु ऊर्जा संयंत्रों में गरम होती है।

इस कूलम्ब बाधा को दूर करने के लिए, प्लाज्मा तापमान ( T ) में वृद्धि की आवश्यकता होती है, जो कि MKT के स्कूल पाठ्यक्रम से सभी को याद है, सूत्र द्वारा प्लाज्मा ( v ) में औसत कण वेग के साथ जुड़ा हुआ है

$$

$$mv ^ 2 = 3k_ \ mathrm {B} T$$

जहां m कणों का द्रव्यमान है, और $$$k_ \ mathrm {B}$ - बोल्ट्जमन स्थिरांक ।

लेकिन, आइए कल्पना करें कि हमने दो हाइड्रोजन नाभिकों को एक निश्चित कण में संयोजित किया है, जहां वे पहले से ही करीब हैं, और इसलिए उनके लिए बाकी अवरोध पहले से ही बहुत छोटा है। तब हमें इन कणों को तेजी से बढ़ाने की आवश्यकता होगी (पढ़ें: हमें कम तापमान की आवश्यकता है) ताकि उन्हें कुछ नए में मिलाया जा सके। और इस तरह की भूमिका को एक मध्यवर्ती आयन की भूमिका निभानी चाहिए $$$(\ mathrm {{} ^ nH} \ mu ^ - \ mathrm {{} ^ mH}} ^$ , हाइड्रोजन अणु के आयन का एक एनालॉग $$$\ mathrm {H} _2 ^ + = (\ mathrm {वह ^ -H}) ^ +$ ।
इन दोनों कणों के बीच के अंतर की जांच करने पर, हम महसूस करेंगे कि थर्मोन्यूक्लियर संलयन के इग्निशन तापमान को कम करने में म्यूऑन कितना प्रभावी है।

MILK MO LKAO विधि

तो, हमारे पास हमारी आणविक प्रणाली है, जिसमें एक चार्ज + ई (एक इलेक्ट्रॉन चार्ज मोडुलो) और एक कण (इलेक्ट्रॉन या म्यूऑन) के साथ 2 हाइड्रोजन नाभिक शामिल हैं। हमारी प्रणाली, जब तक यह अन्य कणों से टकराती है, तब तक इसे अलग किया जाता है, और इसलिए इसकी ऊर्जा अपने घटक भागों में विघटित हो सकती है:

$$

$$E = T (\ mathrm {H} _1) + T (\ mathrm {H} _2) + \ _ अंडरब्रेस {T (\ mathrm {e} ^ - / \ mu ^ -) + V (\ mathrm {H_1) पाठ {from} H_2}) + V (\ mathrm {\ mathrm {e} ^ - / \ mu ^ - \ text {} \ mathrm {H} _1}) + V (\ mathrm {\ mathrm {e} ^ -) / \ mu ^ - \ text {k} \ mathrm {H} _2})} _ {E_ \ mathrm {e}}$$

जहां पहले दो शब्द ( $$$T (\ mathrm {H} _1)$ और $$$T (\ mathrm {H} _2)$ ) हाइड्रोजन नाभिक की गतिज ऊर्जा, तीसरा शब्द है ( $$$T (\ mathrm {e} ^ - / \ mu ^ -)$ ) एक नकारात्मक कण (इलेक्ट्रॉन या म्यूऑन) की गतिज ऊर्जा, चौथा शब्द है $$$V (\ mathrm {H_1 \ text {from} H_2})$ क्या एक दूसरे से हाइड्रोजेन के कूलम्ब के प्रतिकर्षण की ऊर्जा है, और शेष दो प्रत्येक प्रोटॉन में इलेक्ट्रॉन / म्यूऑन के कूलम्ब आकर्षण हैं। सामान्य स्थिति में, यह एक 3-शरीर की समस्या है, बस एक क्वांटम है। स्वाभाविक रूप से, माथे में इसे हल करना बहुत मुश्किल है। लेकिन, सौभाग्य से, नाभिक इलेक्ट्रॉन की तुलना में कम से कम 1800 गुना भारी है, और म्यूऑन से 10 भारी है, इसलिए वे छोटे नकारात्मक कणों की तुलना में स्पष्ट रूप से धीमी गति से आगे बढ़ेंगे। इसके कारण, आप पहली बार समस्या को हल कर सकते हैं: पहला, उन गतियों की ऊर्जा खोजें, जो नाभिक की गति से संबंधित नहीं हैं, अर्थात्। $$$E_ \ mathrm {e}$ और फिर पूरी ऊर्जा। ऐसा दिखता है।

1. एक दूसरे के सापेक्ष हाइड्रोजन नाभिक की व्यवस्था का चयन किया जाता है, और यह उन दोनों के बीच और इलेक्ट्रॉन / म्यूऑन के साथ कूलम्ब बातचीत को निर्धारित करता है। कूलंब की क्षमता $$$V (R) = k \ frac {q_1q_2} {R}$ केवल कण आवेशों पर निर्भर करता है $$$q_i$ और उनके बीच की दूरी, इसलिए सभी हाइड्रोजन समस्थानिकों के लिए यह मान समान होगा। इसके अलावा, इन नाभिक के क्षेत्र में एक इलेक्ट्रॉन / म्यूऑन की गति की समस्या हल हो जाती है। यह एक शरीर का कार्य है।
2. ये ऊर्जा $$$E_ \ mathrm {e}$ एक दूसरे के सापेक्ष नाभिक की सभी संभावित व्यवस्थाओं के लिए गणना की जाती है, और यह नाभिक की गति की प्रभावी संभावित ऊर्जा होगी। हमारे मामले में, हमें एक दूसरे के सापेक्ष विभिन्न दूरी पर ऊर्जाओं की गणना करने की आवश्यकता है, इसलिए नाभिक की एक जोड़ी की संभावना हमेशा एक आयामी होती है। ठीक है, तो हमें केवल एक दूसरे के सापेक्ष दो हाइड्रोजन समस्थानिकों की गति की दो-शरीर की समस्या को हल करने की आवश्यकता है।

जाहिर है, हमारे साथ समस्या की जड़ नाभिक के क्षेत्र में इलेक्ट्रॉन / म्यू ऊर्जा की गणना है $$$E_ \ mathrm {e}$ । वास्तव में, यह रासायनिक बंधन है: एक निश्चित क्षमता जो कुछ स्थानों पर नाभिक को एक साथ रखती है। और रासायनिक बंधन की ऊर्जा खोजने का यह बहुत ही काम क्वांटम रसायन विज्ञान में मुख्य है।

दुर्भाग्य से, म्यूऑन और इलेक्ट्रॉन दोनों क्वांटम कण हैं, इसलिए, इस ऊर्जा को खोजने के लिए, हमें क्वांटम यांत्रिकी के तरीकों का सहारा लेना होगा। वास्तव में, दो समान नाभिकों के क्षेत्र में एक इलेक्ट्रॉन / म्यूऑन की गति की हमारी समस्या को स्पष्ट रूप से ( यहां देखें) हल किया जाता है, लेकिन यह समाधान बहुत जटिल है और परिणाम हाइड्रोजन जैसे परमाणु के मामले में उतना स्पष्ट नहीं है। इसलिए, हम एक अलग, अनुमानित दृष्टिकोण को अलग करने की कोशिश करेंगे, जो किसी भी सिस्टम पर लागू होता है। यह तथाकथित है आणविक ऑर्बिटल्स, परमाणु ऑर्बिटल्स के रैखिक संयोजनों या MO LKAO के रूप में विधि।

आइए हाइड्रोजन नाभिक के क्षेत्र में इलेक्ट्रॉन / म्यूऑन की गति के लिए श्रोडिंगर समीकरण पर करीब से नज़र डालें:

$$

$$\ टोपी {H} \ psi = \ underbrace {\ left (\ overbrace {- \ frac {1} {2m} (\ frac {\ आंशिक ^ 2} {\ आंशिक x ^ 2} + \ frac {आंशिक ^} 2} {\ आंशिक y ^ 2} + \ frac {\ आंशिक ^ 2} {\ आंशिक z ^ 2})} ^ {\ hat {T}} + \ overbrace {- \ frac {1} {R_1}} ^ {{टोपी {V} _1} + \ _ ओवरब्रेस {- \ frac {1} {R_2}} ^ {\ hat {V} _2} + \ overbrace {\ frac {1} {R}} ^ {{टोपी} V } _ \ _ mathrm {HH}} \ right)} _ {\ hat {H}} \ psi = E \ psi$$

यह समीकरण इकाइयों की परमाणु प्रणाली ( पिछले भाग में PS देखें) में लिखा गया था, इसलिए, हाइड्रोजन नाभिक और इलेक्ट्रॉन / म्यूऑन का चार्ज क्रमशः +1, - 1 है, इलेक्ट्रॉन द्रव्यमान m = 1 है, और monon m207 के लिए।

और यदि आप एक करीब से देखते हैं, तो आप देख सकते हैं कि हैमिल्टन में आप केवल एक नाभिक के चारों ओर एक नकारात्मक कण की गति के साथ शुद्ध रूप से जुड़े एक टुकड़े का चयन कर सकते हैं, जो हाइड्रोजन परमाणु का सिर्फ हैमिल्टन है, और इसे 2 तरीकों से किया जा सकता है:

$$

$$\ hat {H} = (\ overbrace {\ hat {T} + \ hat {V} _1} ^ {\ hat {H} _ {1}} + \ hat {V} _2 + \ hat {V} _ \ mathrm {HH}) = (\ overbrace {\ hat {T} + \ hat {V} _2} ^ {\ hat {H} _ {2}} + \ hat {V} _1 + \ hat {V} _ \ mathrm {HH})$$

हाइड्रोजन जैसे परमाणु के हैमिल्टन के बाहर ( $$$\ _ {H} _i, \ i = $ 1.$ ) हमारे पास हमेशा 2 टुकड़े होते हैं: एक इलेक्ट्रॉन के संपर्क की ऊर्जा / एक अन्य नाभिक के साथ म्यूऑन ( $$$\ _ {V} _j$ ) और परमाणु प्रतिकर्षण ऊर्जा ( $$$\ hat {V} _ \ mathrm {HH}$ )। उनमें से दूसरा इलेक्ट्रॉनों की गति को बिल्कुल भी प्रभावित नहीं करता है - यह एक निश्चित मात्रा में ऊर्जा की एक पारी है, लेकिन एक अन्य नाभिक के साथ एक इलेक्ट्रॉन की बातचीत एक महत्वपूर्ण बात है।
हम सोच सकते हैं कि किसी भी क्षण हमारा कण केवल एक नाभिक के चारों ओर घूमता है, और दूसरे के साथ बातचीत सिर्फ एक सुधार है। नाभिक में से एक के चारों ओर घूमने की विधि के रूप में, हम मान सकते हैं कि इलेक्ट्रॉन / म्यूऑन जमीन (1 एस) की स्थिति में है, जिसके लिए तरंग फ़ंक्शन पिछले भाग से अच्छी तरह से जाना जाता है:

$$

$$| 1 s \ rangle = \ frac {1} {\ sqrt {\ pi}} \ exp \ left (- \ frac {R} {R_1} \ right)$$

जहाँ $$$R_1$ एक कण के लिए बोहर त्रिज्या है। एक इलेक्ट्रॉन के मामले में $$$R_1 = 1$ बोरान (जो कि इलेक्ट्रॉन के लिए बोह त्रिज्या है, लगभग 0.5 एंग्स्ट्रॉम के बराबर है), और एक मेसन के मामले में $$$R_1 = \ frac {1} {m_ \ mu} \ लगभग \ frac {1} {207}$ ।
किसी तरह से 2 नाभिक के क्षेत्र में इलेक्ट्रॉन / म्यूऑन तरंग फ़ंक्शन का अनुमान लगाने के लिए, हम निम्नलिखित कार्य करने की कोशिश कर सकते हैं:

$$

$$\ psi \ लगभग c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle$$

और फिर हमारे साथ एक जटिल आंशिक अंतर समीकरण को हल करने की समस्या 2 अज्ञात गुणांक c ₁ और c _{2 की} खोज करने के लिए कम हो गई है। यह गुणांक (वैज्ञानिक का एक रेखीय संयोजन) परमाणु 1s ऑर्बिटल्स के साथ योग के रूप में प्रस्तुत किया गया बहुत आणविक कक्षीय है।

स्वाभाविक रूप से, हमें इन मापदंडों के लिए एक समीकरण की आवश्यकता है। और यह काफी सरल है यदि आप इस सन्निकटन को श्रोडिंगर समीकरण में प्रतिस्थापित करते हैं $$$\ _ {H} \ psi = E \ psi$ :

$$

$$\ hat {H} (c_1 | 1s_1 \ rangle + c_2 | 1s_2 \ rangle) = c_1 \ hat {H} | 1s_1 \ rangle + c_2 \ hat {H} | 1s_2 \ rण = e (c_1 | 1s_1 \ rangle +) c_2 | 1s_2 \ rangle) = c_1 E | 1s_1 \ rangle + c_2 E | 1s_2 / r$$

दरअसल, हम चाहते हैं कि यह अनुपात हर जगह संतुष्ट हो, इसलिए हम किसी तरह इस सभी के औसत मूल्यों की गणना कर सकते हैं। हम इस समीकरण को बाईं ओर से गुणा करते हैं $$$<1s_1 |$ और $$$<1s_2 |$ और सभी निर्देशांक पर एकीकृत। नतीजतन, हम 2 रैखिक समीकरणों की एक प्रणाली प्राप्त करते हैं, जहां गुणांक ₁ , सी ₂ और ऊर्जा ई खोजने के लिए आवश्यक है:

$$

$$\ start {pmatrix} \ langle 1s_1 | \ hat {H} | 1s_1 \ rangle & \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle \\ \ langle 1s_2। \ टोपी {H}। 1s_1 \ rangle & \ _ langle 1s_2 | \ hat {H} | 1s_2 \ rangle \\ \ end {pmatrix} \ start {pmatrix} c_1 \\ c_2 \ end {pmatrix} = E \ start {pmatrix} / langle 1s_1 | 1s_1 \ rangle & \ langle 1s_1 | 1s_2 \ rangle \\ \ langle 1s_2 | 1s_1 \ rangle & \ l 1 1s_2 | 1s_2 \ rangle \\ \ end {pmatrix} \ start {pmatrix} c \\ c_2 \ end {pmatrix}$$

जिस किसी ने भी रैखिक बीजगणित का अध्ययन किया है, वह एक सामान्यीकृत eigenvector-eigenvalue समस्या को पहचान लेगा। इसे हल करने से पहले, हम विश्लेषण करेंगे कि मौजूदा मैट के 2 मैट्रिसेस के तत्व क्या हैं, (एक ही समय में हम एक अक्षर के साथ उनके छोटे पदनाम का परिचय देते हैं)।

• चलो सबसे सरल से शुरू करते हैं: $$$\ langle 1s_1 | 1s_1 \ rangle = \ langle 1s_2 | 1s_2 \ rangle = 1$ - यह तरंग कार्यों का सामान्यीकरण है, और जैसा कि हम याद करते हैं, इलेक्ट्रॉन / म्यूऑन को खोजने की कुल संभावना कम से कम 1 कहीं है।
• $$$\ langle 1s_1 | 1s_2 \ rangle = \ langle 1s_2 | 1s_1 \ rangle = S$ - यह तथाकथित है ओवरलैप इंटीग्रल, यह दर्शाता है कि प्रत्येक परमाणुओं के लिए 1 एस इलेक्ट्रॉन बादल कैसे ओवरलैप करते हैं।
• $$$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ alp$ । इस अभिन्न अंग में कई भाग होते हैं:
  

  $$

  $$\ langle 1s_1 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ l 1 1s_1 = \ hat {H} _1 | 1s_1 \ rangle} _ {- \ frac {m {{2}} + \ langle 1s_1 \ टोपी {V} _2 | 1s_1 \ rangle + \ frac {1} {R}$$
  
  
• $$$\ langle 1s_1 | \ hat {H} | 1s_2 \ rangle = \ langle 1s | hd / \ hat {H} | 1s_1 \ rangle = \ beta$ । यहाँ यह समान है:
  

  $$

  $$\ langle 1s_2 | \ hat {H} | 1s_1 \ rangle = \ underbrace {\ langle 1s_2 | \ overbrace {\ hat {H} _1 | 1s_1 \ rangle} ^ {- \ frac {m {{2} | 1s_1 \ rangle}} {{\ frac {m} {2} S} + की langle 1s_2 | hat {V} _2 | 1s_1 \ rangle + \ frac {S} {R}$$
  
  यानी एक हाइड्रोजन जैसे परमाणु और आंतरिक परमाणु प्रतिकर्षण की ऊर्जा, जो ओवरलैप इंटीग्रल (पहली और अंतिम शर्तों) द्वारा मापी जाती है, और, जैसा कि यह था, इलेक्ट्रॉन / म्यूऑन की ऊर्जा एक परमाणु से दूसरे में hopping है।
  

आइए हम फिर से लिखे समीकरण से हमारे हाइड्रोजन जैसी आयन की ऊर्जाओं के लिए भावों को खोजें

$$

$$\ start {pmatrix} \ Alpha & \ Beta \\ \ beta & \ Alpha \ end {pmatrix} \ start {pmatrix} s_1 \\ c_2 \ end {pmatrix} = E \ start {pmatrix} & S \\ S & 1 \ end {pmatrix} \ start {pmatrix} c_1 \\ c_2 \ end {pmatrix}$$

समीकरण को हल करने के लिए आवश्यक ऊर्जा खोजने के लिए:

$$

$$\ det \ start {pmatrix} \ alpha -E & \ beta -ES \\ \ beta - ES & \ Alpha -E \ end {pmatrix} = ((अल्फा -E) ^ 2 - (\ Beta - ES) ^ 2 = 0$$

जहां "डिट" रूसी के निर्धारक (मैट्रिक्स का निर्धारक) को दर्शाता है।

E के संबंध में इस द्विघात समीकरण के हल हैं:

$$

$$E_ \ pm = \ frac {\ अल्फा \ pm \ बीटा} {1 \ pm S} = - \ frac {m} {2} + \ frac {1} {R} + \ frac {\ _ langle 1s_1। \ / टोपी | {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle} {1 \ pm S}$$

पहला टुकड़ा स्पष्ट रूप से परमाणु की ऊर्जा है, दूसरा आंतरिक परमाणु प्रतिकर्षण है, वही कूलम्ब अवरोधक जो थर्मोन्यूक्लियर प्रतिक्रिया के प्रज्वलन को रोकता है, और अंतिम जटिल संरचना से निपटा जाना चाहिए।

यदि हम आंतरिक परमाणु प्रतिकर्षण को त्याग देते हैं, जो कि इलेक्ट्रॉन / म्यूऑन ऊर्जा के लिए केवल एक संदर्भ बिंदु है, तो हम पाते हैं कि हमारे पास ऊर्जा के साथ दो राज्य हैं

$$

$$\ epsilon_ \ pm = - \ frac {m} {2} + \ frac {\ _ l 1 1s_1 | \ hat {V} _2 | 1s_1 \ rangle \ pm \ langle 1s_2। \ _ \ _ {v} _2 | 1s_1 \ rangle} {1 \ pm एस}$$

चूंकि दोनों तरंग कार्य करती हैं $$$| 1s_1 \ rangle$ और $$$| 1s_2 \ rangle$ - सकारात्मक, और $$$\ _ {V} _i <0$ (क्योंकि ऋणात्मक कण हमेशा धनात्मक की ओर खींचा जाता है), तब $$$\ epsilon_ + <- \ frac {m} {2}$ (एक परमाणु की ऊर्जा), और $$$\ epsilon _-> - \ frac {m} {2}$ , यानी। हमें आणविक कक्षाओं की एक मानक तस्वीर मिलती है:



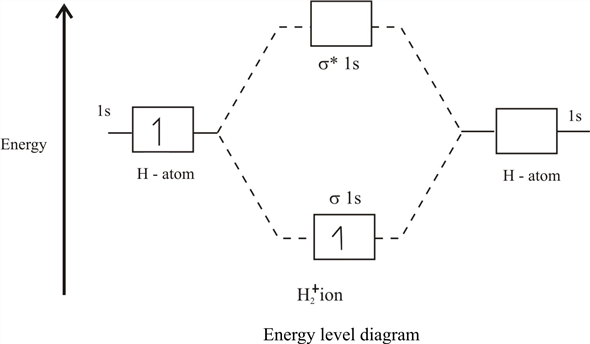
ऊर्जा के साथ कम कक्षीय $$$E _ +$ बाध्यकारी कहा जाता है, और शीर्ष (ऊर्जा के साथ) $$$ई _-$ ) - विरोधी बाध्यकारी, या ढीला। नतीजतन, यदि एक इलेक्ट्रॉन / म्यूऑन निचले आणविक कक्षीय पर बैठता है, तो यह लगभग 2 नाभिकों को एक के आसपास से उड़ान भरने से लाभान्वित करता है, और इसके आंदोलन के साथ यह सिस्टम की कुल ऊर्जा को कम करता है। और यह बहुत ही जादुई रासायनिक बंधन है जो आंतरिक प्रतिकर्षण को स्क्रीन करता है, जिससे नाभिक काफी समय तक एक दूसरे के बगल में रहते हैं।

और यहां हाइड्रोजन बांड के इंटीग्रल्स की गणना यह समझने के लिए की जानी चाहिए कि हाइड्रोजन नाभिक को कितनी बारीकी से अनुमति दी जाती है। वास्तव में, सभी तीन मांग के बाद अभिन्न की गणना विश्लेषणात्मक रूप से की जाती है, लेकिन यह बहुत अधिक रक्तस्रावी और जटिल है (कोई भी दिलचस्पी है, अध्याय 9 को फ़्लेरी की क्वांटम रसायन विज्ञान की पुस्तक में देखें )। इसलिए, हम मोंटे कार्लो विधि का उपयोग करके अलग-अलग तरीके से सरल, और इन अभिन्न गणना करेंगे।

महानगर विधि

मैं अपने दादा: सैन्य परमाणु, और अधिक विशेष रूप से मैनहट्टन परियोजना को श्रद्धांजलि देने के लिए थर्मोन्यूक्लियर ऊर्जा के बारे में पाठ में इसे बहुत तार्किक मानता हूं। यह उससे था कि मोंटे कार्लो विधि विकसित हुई, और विशेष रूप से मेट्रोपोलिस एल्गोरिथ्म , जिनमें से एक लेखक, एडवर्ड टेलर, "हाइड्रोजन बम का पिता" है (वह व्यक्ति, जिसने एनवेटॉक एटोल पर थर्मोन्यूक्लियर संलयन लॉन्च किया था)।


सामान्य तौर पर, हम विधि के सार का विश्लेषण करेंगे। यह सांख्यिकीय यांत्रिकी के कार्यों के लिए अभिप्रेत है। इसमें मुख्य वितरण बोल्ट्जमैन वितरण है: एक निश्चित राज्य में एक प्रणाली का पता लगाने की संभावना है $$$\ exp (- \ beta E)$ । $$$\ बीटा ^ {- 1} = k_ \ mathrm {B} T$ । और थर्मोडायनामिक संतुलन में प्रणाली के लिए कुछ पैरामीटर ए का मनाया मूल्य अभिन्न के बराबर है

$$

$$\ langle A \ rangle = \ frac {1} {Z} \ int A (q) \ exp (- \ beta E (q)) dq$$

जहाँ q वह निर्देशांक है जो सिस्टम की स्थिति को मापता है (उदाहरण के लिए, कणों के निर्देशांक / संवेग), और Z को सामान्यीकरण कारक कहते हैं जिसे विभाजन फ़ंक्शन कहा जाता है:

$$

$$Z = \ int \ exp (- \ beta E (q)) dq$$

यदि सिस्टम में बहुत सारे कण हैं, तो माथे में किसी भी अभिन्न अंग की गिनती पूरी तरह से अवास्तविक है। भोली मोंटे कार्लो विधि, जिसमें हम बस यादृच्छिक q निर्देशांक का एक गुच्छा का चयन करते हैं, कुछ भी सार्थक नहीं देगा यदि सिस्टम की वास्तव में संभव स्थिति है जिसके लिए संभावना है $$$\ exp (- \ beta E)$ बिल्कुल गैर-शून्य, बहुत कम। और यह ऐसे मामलों के लिए ठीक है कि हमें महत्व द्वारा एक नमूना की आवश्यकता है, जिसमें हम एल्गोरिथ्म को केवल राज्य स्थान में पर्याप्त रूप से संभावित स्थानों के नमूने की अनुमति देते हैं।

मेट्रोपोलिस एल्गोरिथ्म इस प्रकार है।

1. सिमुलेशन की शुरुआत करते समय, हम कॉन्फ़िगरेशन स्पेस में कुछ शुरुआती सन्निकटन का चयन करते हैं $$$\ mathbf {q} ^ {(0)}$ और अधिकतम संभव वेतन वृद्धि के कुछ वेक्टर $$$\ delta \ mathbf {q}$ । प्रारंभिक बिंदु पर, हम सिस्टम की ऊर्जा की गणना करते हैं $$$E ^ {(0)} = E (\ mathbf {q} ^ {(0)})$ (पढ़ें - संभावना $$$p = \ exp (- \ Beta E ^ {(0)})$ )।
2. Nth कदम पर नया विन्यास इस प्रकार है।
   
   1. परीक्षण कॉन्फ़िगरेशन की ऊर्जा की गणना करें $$$E_ \ mathrm {परीक्षण} = E (\ mathbf {q} _ \ mathrm {परीक्षण})$ (यानी संभावना $$$p_ \ mathrm {परीक्षण} = \ exp (- \ बीटा E_ \ mathrm {परीक्षण})$ )।
   2. और फिर हम पुरानी संभावना की तुलना करते हैं $$$p ^ {(n)}$ परीक्षण के साथ $$$p_ \ mathrm {परीक्षण}$
      
      
      • यदि नए कॉन्फ़िगरेशन में अधिक या समान संभावना है ( $$$\ frac {p_ \ mathrm {परीक्षण}} {p ^ {(n)}} \ geq 1$ ), या, समकक्ष, नए बिंदु की ऊर्जा कम या पुरानी के समान है ( $$$E_ \ mathrm {परीक्षण} \ leq E ^ {(n)}$ ), फिर नया बिंदु स्वीकार किया जाता है और सिस्टम इसमें चला जाता है ( $$$q ^ {(n + 1)} = q_ \ mathrm {परीक्षण}$ )
      • यदि परीक्षण कॉन्फ़िगरेशन ऊर्जा में अधिक है ( $$$E_ \ mathrm {परीक्षण}> E ^ {(n)}$ ), जो समकक्ष है $$$\ frac {p_ \ mathrm {परीक्षण}} {p ^ {(n)}} <1$ , तो इस मामले में हम एक यादृच्छिक संख्या उत्पन्न करते हैं $$$P \ [0; 1) $ मे$ एक समान वितरण से, और इसे संभावनाओं के अनुपात से तुलना करें, जो कि संक्रमण संभावनाएं हैं। अगर $$$P <\ frac {p_ \ mathrm {परीक्षण}} {p ^ {(n)}}$ , तो हम एक नया बिंदु स्वीकार करते हैं, और यदि नहीं ( $$$P \ geq \ frac {p_ \ mathrm {परीक्षण}} {p ^ {(n)}}$ ), फिर हम अस्वीकार करते हैं, और सिस्टम पुराने कॉन्फ़िगरेशन में रहता है ( $$$q ^ {(n + 1)} = q ^ {(n)}$ ) ...
      
      
   
   
3. उपरोक्त एल्गोरिथ्म के अनुसार कई कदम उठाते हुए, हम सिस्टम कॉन्फ़िगरेशन के संभावित स्थान का एक महत्वपूर्ण (अर्थात, वास्तव में महत्वपूर्ण) नमूना लेते हैं। हमारे लिए अभिन्न अभिन्न सूत्र द्वारा गणना की जाती है:
   $$$\ langle A \ rangle = \ frac {1} {Z} \ int A (\ mathbf {q}) \ exp (- \ beta E (\ mathbf {q})) d \ mathbf {q} = frac { 1} {N} \ sum_ {n = 0} ^ {N} A (\ mathbf {q} ^ {(n)})$
   

यह मेट्रोपोलिस एल्गोरिथ्म कैसे काम करता है।

और अब इसे 3 अभिन्नों की गणना के लिए अनुकूलित करना आवश्यक होगा जो हमें ब्याज देते हैं। आइए उन्हें अधिक विस्तार से देखें।

• $$$S (R) = \ langle 1s_2 | 1s_1 \ rangle = \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} ^ int_ सीमाएं _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-m \ underbrace) {| \ mathbf {r} - / mathbf {r} _2 | } _ {R_2})} _ {1s_2}} ^ {A ((mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ _ pi} \ exp (-m \) अंडरब्रेस {| \ mathbf {r} - \ mathbf {r} _1 |} _ {R_1})} _ {1s_1}}} ^ {p (\ mathbf {r})} dx dy dz 10$ जहाँ $$$\ mathbf {r} = (x, y, z) ^ \ mathbf {T}$ - इलेक्ट्रॉन / म्यूऑन के निर्देशांक, $$$\ mathbf {r} _i = (x_i, y_i, z_i) ^ \ mathbf {T}$ हाइड्रोजन नाभिक के निर्देशांक हैं, और $$$R_i = | \ mathbf {r} - \ mathbf {r} _i | = \ sqrt {(x-x_i) ^ 2 + (y-y_i) ^ 2 + (z-z_i) ^ 2}$ - सकारात्मक और नकारात्मक कणों के बीच की दूरी,
  
• $$$\ langle 1s_1 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} \ int \ सीमाएं _ {- \ infty} ^ {+ infty} \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ pi}} \ exp (-mR_1)} _ {1s_1}} / frac {1} {R_2} } ^ {A ((mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ _ pi}} \ exp (-mR_1)} _ {1ss}}} ^ {p (\ _) mathbf {r})} dxdydz$
• $$$\ langle 1s_2 | \ hat {V} _2 | 1s_1 \ rangle = - \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} \ int \ सीमाएं _ {- \ infty} ^ {+ infty} \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ _ pi}} \ exp (-mR_2)} _ {1s_2}} frac {1} {R_1} } ^ {A ((mathbf {r})} \ cdot \ overbrace {\ underbrace {\ frac {1} {\ sqrt {\ _ pi}} \ exp (-mR_1)} _ {1ss}}} ^ {p (\ _) mathbf {r})} dxdydz$

यह देखा जा सकता है कि, यदि हम प्रायिकता p के लिए परमाणुओं में से 1-फ़ंक्शन की गणना करते हैं,


तब अभिन्न के संकेत के तहत बाकी सब (दूसरी लहर फ़ंक्शन और 3 में से 2 मामलों में इलेक्ट्रॉन / नाभिक के नाभिक के आकर्षण की क्षमता) एक ऐसा फ़ंक्शन होगा जिसका औसत मूल्य गणना की जाती है। मेट्रोपोलिस विधि द्वारा सामान्य गणना के विपरीत, केवल एक चीज को करना होगा, अभिन्न के सामान्यीकरण को सीधा करना है। तथ्य यह है कि मानक सामान्यीकरण पर होगा

$$

$$Z = \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty} \ int \ सीमाएं _ {- \ infty} ^ {+ \ infty \ "exp (-m R) dx डाई dz = 4 \ pi \ int \ limit_ {0} ^ {+ \ infty} \ exp (-m R) R ^ 2 dR = \ frac {8 \ pi} {m ^ 3}$$

और हमें इसके सामान्यीकरण की आवश्यकता है $$$\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}$ जहाँ

$$

$$\ langle 1s_1 | 1s_1 \ rangle = \ int \ सीमाएँ _ {- \ infty} ^ {+ \ infty} \ int \ limit _ {- \ infty} ^ {+ \ infty} \ int \ सीमाएँ _ {- \ infty} ^ \ _ \ infty} \ _ exp (-2 m R) dx डाई dz = 4 \ pi \ int \ limit_ {0} ^ {+ \ infty} \ exp (-2m R) R ^ 2 dR = \ frac {\ pi} {m ^ 3}$$

इसका मतलब यह है कि मेट्रोपोलिस के अनुसार गणना किए गए प्रत्येक अभिन्न को एक कारक से गुणा करना होगा

$$

$$\ frac {Z} {\ sqrt {\ langle 1s_1 | 1s_1 \ rangle}} = 8 \ sqrt {\ frac {\ pi} {m ^ 3}}$$

यह पहले से ही एक निश्चित स्क्रिप्ट के रूप में व्यवस्थित किया जा सकता है, उदाहरण के लिए, पायथन में (उदाहरण के लिए, कोड नीचे है)।


ऐसी गणनाओं का उपयोग करके, हम अंत में हाइड्रोजन आयन में संभावित ऊर्जाओं की तुलना कर सकते हैं $$$\ mathrm {H} _2 ^ +$ और इसके म्यूऑन समकक्ष।

$$$\ mathrm {H_2 ^ + = p ^ + e ^ - p ^ +}$ बनाम $$$\ mathrm {p ^ + \ mu ^ - p ^ +}$

इसलिए, एक स्क्रिप्ट से लैस, हम एक इलेक्ट्रॉन और एक म्यूऑन द्वारा बाध्य हाइड्रोजन नाभिक के दृष्टिकोण की संभावित ऊर्जा की सतह की गणना कर सकते हैं। एक ऊर्जा संदर्भ बिंदु के रूप में, हम परमाणुओं को एक-दूसरे से पतला कर लेते हैं (अर्थात। $$$-m / 2$ , जो नाभिक के बीच की दूरी पर क्षमता के बराबर है $$$R = + \ infty$ )।

एक इलेक्ट्रॉन के मामले में, न्यूनतम के पास की क्षमता इस तरह दिखती है:



न्यूनतम लगभग 2 बोरॉन की दूरी पर होता है (यानी, लगभग 2 परमाणु त्रिज्या का योग), और टुकड़ों में अणु के पृथक्करण की ऊर्जा लगभग 0.06 हार्ट्री है, जो लगभग 20,000 डिग्री केल्विन (या सेल्सियस पर हीटिंग से मेल खाती है, यह यहां कोई फर्क नहीं पड़ता)। ऊर्जा को परिवर्तित करने के लिए, मैं ऑनलाइन संसाधनों का उपयोग करने की सलाह देता हूं, जैसे कि यह ।

एक समान रूप से बाध्य हाइड्रोजन आयन के साथ ऐसी ही स्थिति:



चूंकि मुऑन हाइड्रोजन के लिए बोह त्रिज्या छोटा है ( पिछले भाग को देखें), हाइड्रोजन नाभिक भी न्यूनतम संभावित ऊर्जा पर लगभग 200 गुना बैठते हैं। इस अणु की टूटने की ऊर्जा पहले से ही 10 से अधिक हर्ट्री है, जो तीन से अधिक लीमा डिग्री के तापमान से मेल खाती है ( $$$\ लगभग (3.2 \ cdot 10 ^ 6) ^ \ circ$ )।

प्रज्वलन के लिए, प्रतिक्रियाओं को आमतौर पर 10 ⁸ K के क्रम के तापमान की आवश्यकता होती है , जो लगभग 320 हार्ट्री है। आइए देखते हैं कि साधारण डिओडोरोन आयन के मामले में और इसके चंद्रमा के मामले में एक समान ऊर्जा कितनी दूरी पर प्राप्त होती है:



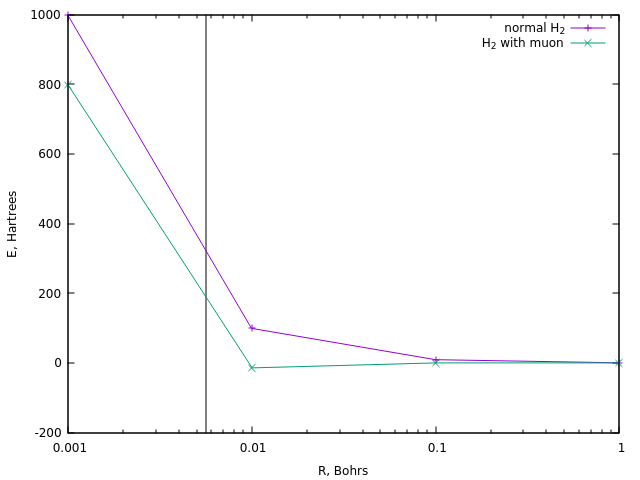
पूर्व के मामले में, यह लगभग 0.0058 बोरॉन (ऊर्ध्वाधर रेखा) की दूरी से मेल खाती है।

मुऑन हाइड्रोजन में एक समान दूरी लगभग 190 हे की ऊर्जा पर प्राप्त की जाती है, अर्थात। लगभग डेढ़ गुना कम। और यह म्यूऑन कैटेलिसिस के तापमान का सबसे सरल अनुमान है।

लेकिन वास्तव में, सब कुछ कूलर भी होगा। तथ्य यह है कि अगर एक स्थिर कण बनता है $$$\ mathrm {({} ^ mH (\ mu ^ -) {} ^ nH) ^ +}$ , फिर ये नाभिक, जबकि म्यून जीवित है, एक दूसरे के सापेक्ष दोलन करेंगे। और यहां "दो हाइड्रोजन परमाणुओं" राज्य से "भारी कोर" राज्य तक टनलिंग हो सकती है, और सुरंग खोदने की संभावना लगभग सुरंगनुमा लंबाई d पर निर्भर करती है। $$$p ^ {- d}$ , ताकि दो न्यूक्लियर को म्यूऑन के करीब लाने से हम इस प्रतिक्रिया के टनलिंग कोर्स की संभावना को काफी बढ़ा देंगे। दुर्भाग्य से, इस आशय के अनुमानों को अब क्वांटम रसायन विज्ञान की आवश्यकता नहीं है, लेकिन परमाणु भौतिकी, इसलिए चर्चा का यह हिस्सा इस पद के दायरे से परे है। तो इस पर हम रोक देंगे।

पुनश्च यह इतना आसान क्यों नहीं है?

वास्तव में, इन कणों को बनाने के लिए प्लाज्मा स्थितियों में इतना सरल नहीं है। तथ्य यह है कि अगर हम दो कणों से टकराते हैं, तो उनकी कुल ऊर्जा स्पष्ट रूप से पृथक्करण ऊर्जा (या आयनीकरण, नाभिक + इलेक्ट्रॉन / म्यूऑन के मामले में) से अधिक हो जाती है, इसलिए जब वे टकराते हैं, तो वे एक स्थिर कण (परमाणु, आयन, अणु) नहीं बनाते हैं, लेकिन उड़ते हैं एक दूसरे को अतीत एक-दूसरे से चिपके रहने के लिए, उन्हें कहीं न कहीं सरप्लस एनर्जी को फेंकने की जरूरत है, और इसके लिए हमें एक थर्ड एक्स्ट्रा चाहिए जो इस एनर्जी को अपनाएगा। यह एक फोटॉन, या पास में किसी तरह का वाम कण उड़ सकता है, लेकिन मुख्य बात यह है कि स्थितियों को अतिरिक्त ऊर्जा के इस प्रवेश में योगदान करना चाहिए।

पी पी एस

यदि आपके पास कोई टिप्पणी / स्पष्टीकरण / प्रश्न हैं, तो टिप्पणी या पीएम में लिखें। मैं सब कुछ ठीक कर दूंगा, मैं हर बात का जवाब दूंगा और समझाऊंगा।