पायथन, एनाकोंडा और अन्य सरीसृप के बिना मशीन सीखने

नहीं, ठीक है, ज़ाहिर है, मैं गंभीर नहीं हूँ। विषय को सरल बनाने के लिए किस हद तक संभव है, इसकी एक सीमा होनी चाहिए। लेकिन पहले चरणों के लिए, मूल अवधारणाओं और विषय में एक त्वरित "प्रविष्टि" की समझ, यह अनुमेय हो सकता है। और इस सामग्री को कैसे ठीक से नाम दिया जाए (विकल्प: "डमी के लिए मशीन सीखना", "डायपर से डेटा का विश्लेषण", "सबसे छोटे के लिए एल्गोरिदम"), हम अंत में चर्चा करेंगे।

व्यापार करने के लिए। उन्होंने डेटा का विश्लेषण करते समय विभिन्न मशीन लर्निंग के तरीकों में होने वाली प्रक्रियाओं के विज़ुअलाइज़ेशन और विज़ुअलाइज़ेशन के लिए एमएस एक्सेल पर कई एप्लिकेशन प्रोग्राम लिखे। विश्वास करना, अंत में, संस्कृति के मीडिया के अनुसार, जिसने इन तरीकों में से अधिकांश को विकसित किया (वैसे, बिना किसी मतलब के सभी। सबसे शक्तिशाली "सपोर्ट वेक्टर विधि", या एसवीएम, सपोर्ट वेक्टर मशीन हमारे कॉम्पिटिटिव व्लादिमीर वेपनिक, मास्को इंस्टीट्यूट ऑफ मैनेजमेंट का एक आविष्कार है)। 1963, वैसे! अब वह, हालांकि, सिखाता है और संयुक्त राज्य अमेरिका में काम करता है)।

समीक्षा के लिए तीन फाइलें

1. K- साधन क्लस्टरिंग

इस तरह के कार्य "एक शिक्षक के बिना सीखने" से संबंधित हैं, जब हमें पहले से ज्ञात कुछ श्रेणियों में प्रारंभिक डेटा को तोड़ने की आवश्यकता होती है, लेकिन साथ ही साथ हमारे पास "सही उत्तरों" की कोई संख्या नहीं होती है, हमें उन्हें डेटा से ही निकालना होगा। आइरिस फूलों की उप-प्रजातियां खोजने की मूलभूत शास्त्रीय समस्या (रोनाल्ड फिशर, 1936!), जिसे ज्ञान के इस क्षेत्र का पहला संकेत माना जाता है - ऐसी प्रकृति का है।

विधि काफी सरल है। हमारे पास वैक्टर (एन संख्या के सेट) के रूप में प्रतिनिधित्व वस्तुओं का एक सेट है। Irises के लिए, ये एक फूल की विशेषता वाले 4 नंबरों के सेट हैं: बाहरी और आंतरिक पेरिंथ पालियों की लंबाई और चौड़ाई, क्रमशः ( आइरिस फिशर - विकिपीडिया )। एक दूरी के रूप में, या वस्तुओं के बीच निकटता का माप, सामान्य कार्टेशियन मीट्रिक चुना जाता है।

इसके अलावा, समूहों के केंद्रों को मनमाने ढंग से चुना जाता है (या मनमाने ढंग से नहीं, नीचे देखें), और प्रत्येक वस्तु से समूहों के केंद्रों की दूरी की गणना की जाती है। इस चलना कदम में प्रत्येक वस्तु को निकटतम केंद्र से संबंधित के रूप में चिह्नित किया गया है। फिर प्रत्येक क्लस्टर के केंद्र को उसके सदस्यों के निर्देशांक के अंकगणितीय माध्य में स्थानांतरित किया जाता है (भौतिकी के साथ सादृश्य द्वारा इसे "द्रव्यमान का केंद्र" भी कहा जाता है), और प्रक्रिया को दोहराया जाता है।

प्रक्रिया जल्दी से पर्याप्त रूपांतरित हो जाती है। द्वि-आयामी में चित्रों में, यह इस तरह दिखता है:

1. विमान पर अंक का प्रारंभिक यादृच्छिक वितरण और समूहों की संख्या



2. समूहों के केंद्रों को परिभाषित करना और उनके समूहों को इंगित करना



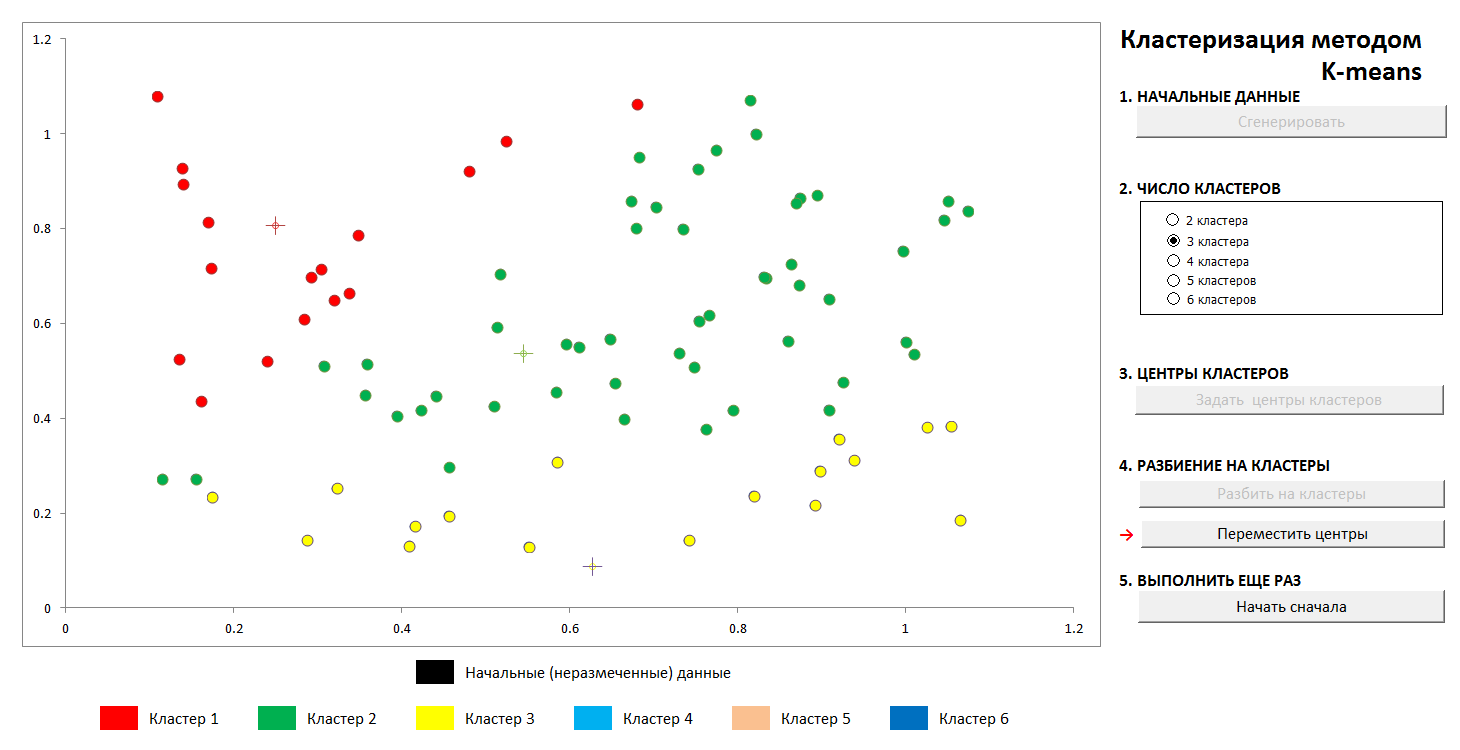
3. समूहों के केंद्रों के निर्देशांक का स्थानांतरण, बिंदुओं का पुनर्गणना, जब तक केंद्र स्थिर नहीं हो जाते। क्लस्टर के केंद्र से अंतिम स्थिति तक का प्रक्षेपवक्र दिखाई देता है।



किसी भी समय, आप नए क्लस्टर केंद्र सेट कर सकते हैं (अंकों के नए वितरण को उत्पन्न किए बिना!) और देखें कि विभाजन प्रक्रिया हमेशा अद्वितीय नहीं होती है। गणितीय रूप से, इसका मतलब है कि अनुकूलित फ़ंक्शन (इसके समूहों के केंद्रों के बिंदुओं से दूरी के वर्गों का योग) के लिए हम एक वैश्विक नहीं, बल्कि एक स्थानीय न्यूनतम पाते हैं। इस समस्या को गुच्छों के प्रारंभिक केंद्रों के एक गैर-यादृच्छिक विकल्प से हराया जा सकता है, या संभव केंद्रों को छांटकर (कभी-कभी उन्हें किसी बिंदु पर बिल्कुल जगह देना फायदेमंद होता है, फिर कम से कम एक गारंटी है कि हम खाली समूहों को नहीं छोड़ेंगे)। किसी भी मामले में, एक परिमित सेट हमेशा एक सटीक निचला बाउंड होता है।

आप इस लिंक पर इस फ़ाइल के साथ खेल सकते हैं (मैक्रो समर्थन को सक्षम करने के लिए मत भूलना। फ़ाइलों की वायरस के लिए जाँच की जाती है)

विकिपीडिया विधि वर्णन - k- साधन विधि

2. बहुपद और डेटा के टूटने से क्षति। पुन: शिक्षा

एक उल्लेखनीय वैज्ञानिक और डेटा विज्ञान के लोकप्रिय के.वी. Vorontsov संक्षेप में मशीन सीखने के तरीकों के बारे में बात करता है "अंक के माध्यम से ड्राइंग के विज्ञान।" इस उदाहरण में, हम सबसे कम वर्ग विधि द्वारा डेटा में पैटर्न पाएंगे।

स्रोत डेटा को "प्रशिक्षण" और "नियंत्रण" में विभाजित करने की तकनीक, साथ ही साथ डेटा के लिए पुनरावृत्ति, या "फिर से शिक्षित करना" जैसी घटना को दिखाया गया है। सही अनुमान के साथ, हमें प्रशिक्षण डेटा पर एक निश्चित त्रुटि और नियंत्रण डेटा पर थोड़ी बड़ी त्रुटि होगी। यदि यह गलत है, तो यह प्रशिक्षण डेटा के लिए एक सटीक समायोजन और नियंत्रण पर एक बड़ी गलती है।

(यह एक सर्वविदित तथ्य है कि एन बिंदुओं के माध्यम से एन-1st डिग्री का एक भी वक्र खींचना संभव है, और यह विधि आम तौर पर वांछित परिणाम नहीं देती है। विकिपीडिया पर लैग्रेग इंटरपोलेशन बहुपद ।

1. हम प्रारंभिक वितरण सेट करते हैं



2. अंक को "प्रशिक्षण" और "नियंत्रण" में 70 से 30 के अनुपात में विभाजित करें।



3. हम प्रशिक्षण बिंदुओं के लिए एक अनुमानित वक्र बनाते हैं, हम उस त्रुटि को देखते हैं जो यह नियंत्रण डेटा पर देता है



4. हम प्रशिक्षण बिंदुओं के माध्यम से सटीक वक्र बनाते हैं, और हम नियंत्रण डेटा (और प्रशिक्षण पर शून्य, लेकिन क्या बात है?) पर एक राक्षसी त्रुटि देखते हैं।



बेशक, "प्रशिक्षण" और "नियंत्रण" सबसेट में एक ही विभाजन के साथ सबसे सरल संस्करण दिखाया गया है, सामान्य मामले में यह गुणांक के सर्वोत्तम समायोजन के लिए बार-बार किया जाता है।

फ़ाइल यहाँ उपलब्ध है, एंटी-वायरस की जाँच की। सही ढंग से काम करने के लिए मैक्रोज़ चालू करें

3. धीरे-धीरे वंश और त्रुटि की गतिशीलता

एक 4-आयामी मामला और रैखिक प्रतिगमन होगा। रेखीय प्रतिगमन गुणांक ढाल ढाल विधि द्वारा चरणों में निर्धारित किया जाएगा, शुरू में सभी गुणांक शून्य हैं। एक अलग ग्राफ त्रुटि को कम करने की गतिशीलता को दिखाता है क्योंकि गुणांक अधिक से अधिक सूक्ष्म रूप से देखते हैं। सभी चार 2-आयामी अनुमानों को देखना संभव है।

यदि आप ग्रेडिएंट डिसेंट स्टेप को बहुत बड़ा सेट करते हैं, तो यह स्पष्ट है कि हर बार हम न्यूनतम को छोड़ेंगे और हम बड़ी संख्या में चरणों में परिणाम पर पहुंचेंगे, हालांकि अंत में हम वैसे भी आएंगे (जब तक कि हम डिसेंट स्टेप को बहुत अधिक स्पर्श नहीं करेंगे, तब एल्गोरिथ्म जाएगा ” रिक्ति में))। और चलना कदम पर त्रुटि की निर्भरता का ग्राफ सुचारू नहीं होगा, लेकिन "झटकेदार"।

1. डेटा उत्पन्न करें, ग्रेडिएंट डिसेंट स्टेप सेट करें



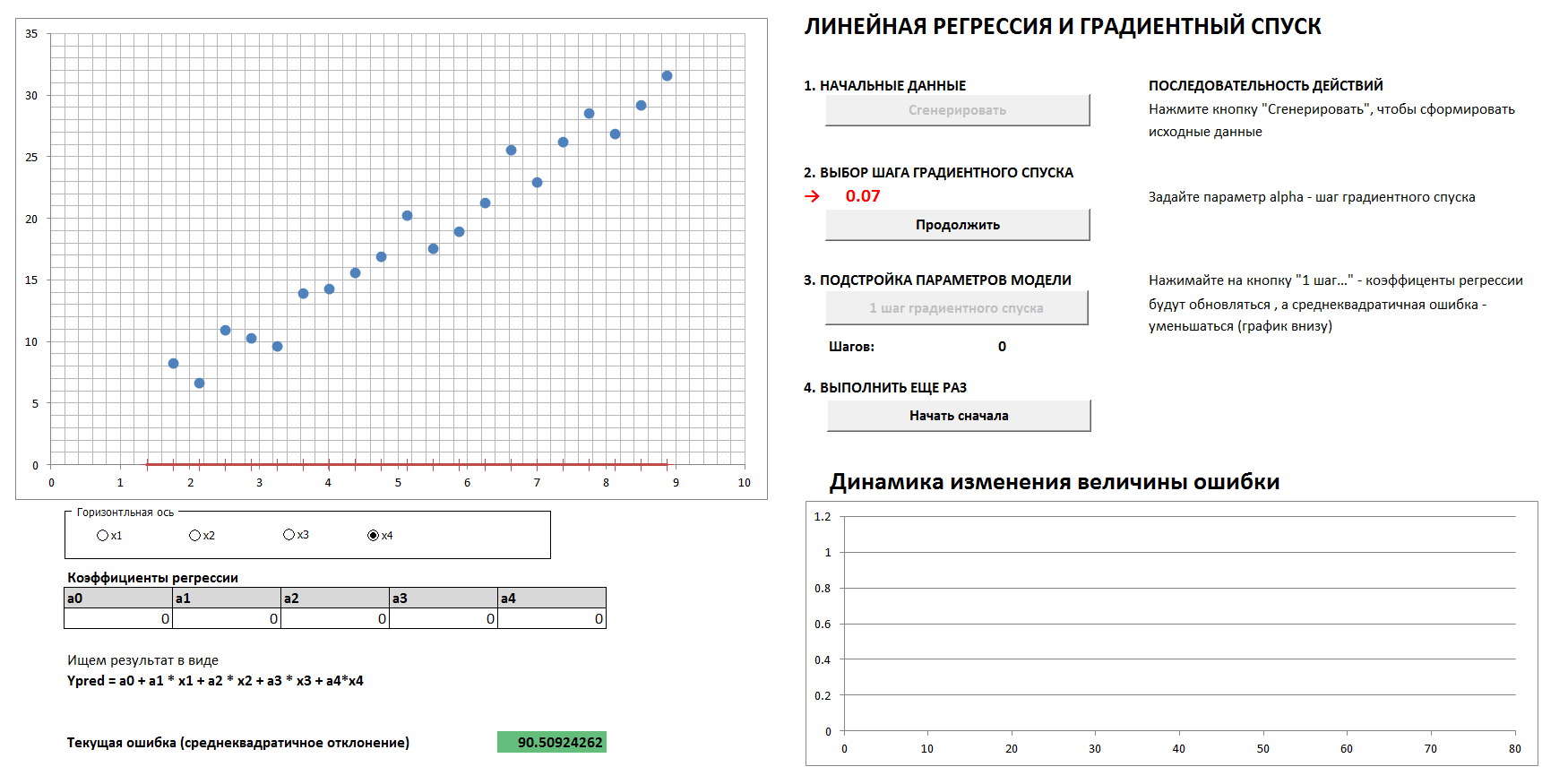
2. ढाल वंश कदम के सही विकल्प के साथ, हम आसानी से और जल्दी से पर्याप्त एक न्यूनतम पर आते हैं



3. अगर ग्रेडिएंट डिसेंट का चरण गलत तरीके से चुना गया है, तो हम अधिकतम को छोड़ देते हैं, त्रुटि ग्राफ "झटकेदार" है, अभिसरण अधिक से अधिक संख्या में कदम उठाता है


और



4. ढाल वंश कदम के पूरी तरह से गलत चयन के साथ, हम न्यूनतम से दूर चले जाते हैं



(चित्रों में दिखाए गए ढाल वंश कदम के मूल्यों के साथ प्रक्रिया को पुन: पेश करने के लिए, "संदर्भ डेटा" बॉक्स की जांच करें)।

फ़ाइल - इस लिंक से, आपको मैक्रोज़ को सक्षम करने की आवश्यकता है, कोई वायरस नहीं है।

एक सम्मानित समुदाय के अनुसार, प्रस्तुति का ऐसा सरलीकरण और तरीका स्वीकार्य है? क्या मुझे लेख को अंग्रेजी में अनुवाद करना चाहिए?