🚒 🥇 🦎 हम एक विद्युत चुम्बकीय तरंग के आगमन की दिशा निर्धारित करने के लिए MUSIC एल्गोरिथ्म का मॉडल बनाते हैं ☂️ ↖️ 🚭

aaspcats

प्रस्तावना

मैं अपना परिचय दूर से शुरू करूंगा। एक बार दूर के 2016-2017 में, आपका विनम्र सेवक छह महीने के प्रशिक्षण पाठ्यक्रम पर सुदूर शहर इलमानौ (जर्मनी) जाने में कामयाब रहा, जहां उसने सफलतापूर्वक (द्वारा और बड़े) मास्टर प्रोग्राम कम्युनिकेशन एंड सिग्नल प्रोसेसिंग को पूरा किया । यह कार्यक्रम एक आसान नहीं था, लेकिन अब इसे याद करना भी सुखद है। कभी-कभी ...

इसलिए, इस प्रशिक्षण के अंत में, डिप्लोमा के अलावा, मेरे पास अभी भी मेरे हाथों में कुछ अलग सामग्री है, जिसे मैंने साझा नहीं करना गलत समझा।

इनमें से एक सामग्री आपके सामने है।

संगोष्ठी की तैयारी करते समय मैंने किन लक्ष्यों का पालन किया :

पहले से स्थापित कुछ के बारे में बात करते हैं, "स्मार्ट" ऐन्टेना सरणियों के विषय में सबसे अधिक सुलभ है और इसे रूसी में करते हैं;
पायथन 3 में एक छोटे से सिमुलेशन का संचालन करने के लिए साथी रेडियो इंजीनियरों को प्रोग्रामिंग भाषाओं पर एक करीब से नज़र डालने के लिए (यदि आपने पहले से करीब नहीं देखा है);
अच्छी अंग्रेजी-भाषा के साहित्य के लिए लिंक प्रदान करें - विदेशी स्रोतों को पढ़े बिना, अब, कहीं नहीं।

क्या विचार करें :

संगीत विधि (MUltiple SIgnal वर्गीकरण) - यह, वास्तव में, पूर्वावलोकन को संदर्भित करता है।

चार्ट बनाने और एमवीडीआर विधि का एक उदाहरण यहां पाया जा सकता है (यदि अतिरिक्त सामग्री के लिए प्रश्न या सुझाव हैं, तो चर्चा जीथब्यू.गिस्ट पर जारी रखी जा सकती है)।

जैसा कि मैंने ऊपर कहा, हम पायथन का उपयोग करेंगे, अर्थात्:

import numpy as np import matplotlib.pyplot as plt

MATLAB, रैखिक बीजगणित मॉडलिंग के लिए सबसे लोकप्रिय और सुविधाजनक उम्मीदवारों में से एक क्यों नहीं है, आप पूछें? क्योंकि, मैं बताना चाहता हूं कि पायथन में भी इसी तरह का काम किया जा सकता है, और MATHAB की तुलना में अजगर का दायरा बहुत व्यापक है। इसलिए, पायथन सिंटैक्स से परिचित होना एक उपयोगी चीज है, मेरी राय में।

चलो शुरू हो जाओ!

सूत्र https://upmath.me/ के माध्यम से तैयार किए जाते हैं। एक महान उपकरण के लिए रचनाकारों का धन्यवाद!

समस्या का बयान

मान लीजिए कि एक रैखिक एंटीना सरणी है जिसमें एक दूसरे से अलग-अलग तत्वों की संख्या होती है $\ Delta = \ frac {\ lambda} {2}$ (एंटीना सरणी का चरण), जहां $\ lambda$ - वाहक विद्युत चुम्बकीय (EM) तरंग की लंबाई।

विद्युत चुम्बकीय तरंगें इस एंटीना सरणी पर विभिन्न दिशाओं से गिरती हैं।

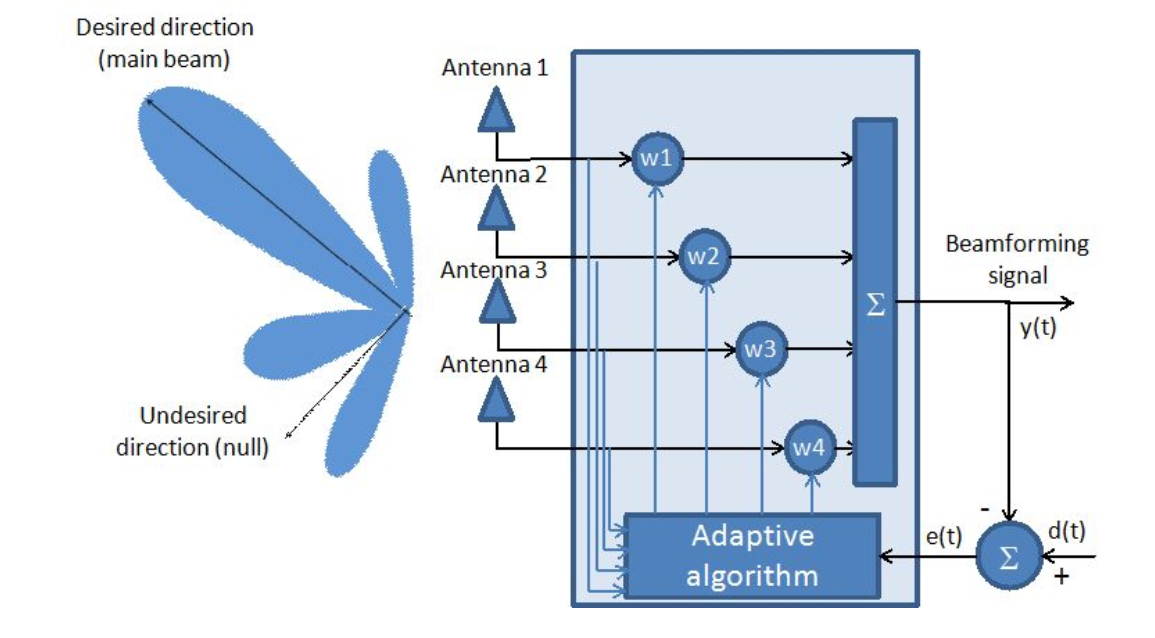
अंजीर। 1. अनुकूली एंटीना प्रणाली।

जैसा कि आंकड़े से देखा जा सकता है, एंटीना सरणी को एक अनुकूली फिल्टर के रूप में माना जाता है।

वास्तव में, गुणांक के इष्टतम वेक्टर को ढूंढना ( $\ mathbf {w} _ {opt}$ ) गणितीय दृष्टिकोण से अनुकूली एंटीना सरणियों का मुख्य कार्य है।

प्रारंभ में, हम यह नहीं जानते हैं कि संकेत किस विशेष दिशा से आ रहे हैं और उनमें से कितने हैं। इस विरोधाभास को हल करना है कि हम उच्च संकल्प के साथ स्थानिक आवृत्तियों का आकलन करने के लिए एक एल्गोरिथ्म का उपयोग करेंगे।

सिग्नल सिमुलेशन प्राप्त किया

हम प्राप्त सिग्नल के मॉडल को सूत्र के माध्यम से प्रस्तुत कर सकते हैं:

$\ mathbf {X} = \ mathbf {A} \ mathbf {S} + \ mathbf {N}$

जहाँ $\ mathbf {A} = [\ mathbf {a} (\ theta_1) \ quad \ mathbf {a} (\ theta_2) \ quad ... \ quad \ mathbf {a} (\ theta_d)$ एंटीना एंटीना की स्कैनिंग वैक्टर (स्टीयरिंग वैक्टर) का मैट्रिक्स ( $a_i = \ exp (-j \ mu m_i)$ । $एम = 0, 1 ... (एम -1)$ । $एम$ - एंटीना सरणी के तत्वों की संख्या, $घ$ - EM तरंगों के स्रोतों की संख्या, $\ The थीटा$ - ईएम लहर के आगमन की दिशा को कोण), $\ mathbf {S}$ - संचरित वर्णों का मैट्रिक्स, और $\ mathbf {N}$ - योजक शोर का मैट्रिक्स।

अंजीर। 2. सर्वदिशात्मक रैखिक एंटीना सरणी (ULAA - एकसमान रैखिक ऐन्टेना सरणी) [1, पी। 32]।

आइए हम इस फॉर्मूले को "रोज़" तरीके से पुनर्विचार करें: अपने ग्रिड पर हमें विभिन्न संकेतों से कुछ "गड़बड़" मिलते हैं, जिन्हें हम द्वारा निरूपित करते हैं $\ mathbf {X}$ । हम स्पष्ट रूप से स्रोतों और दिशाओं की संख्या के बारे में जानकारी प्राप्त नहीं करते हैं, हालांकि, इस बारे में जानकारी प्राप्त संकेत में निहित है।

हम खोजना शुरू कर रहे हैं!

ऐसा करने के लिए, वे आम तौर पर जटिल सिग्नल एम्पलीट्यूड के मेट्रिसेस के साथ खुद को जोड़तोड़ करने के लिए आगे बढ़ते हैं, लेकिन अपने सहकर्मियों के साथ (यानी, संक्षेप में, शक्तियों के साथ):

$\ mathbf {R} _ {xx} = \ mathbf {X} \ mathbf {X} ^ H = \ mathbf {A} \ mathbf {R} _ {ss} \ mathbf {A}: H + \ mathbf {R} _ {nn}$

स्थिति

हम विचार के लिए एक महत्वपूर्ण शर्त पेश करते हैं: रेले कोण संकल्प सीमा:

$sin (\ theta_R) = \ frac {\ lambda} {D}$

जहाँ $D = M \ Delta$ लीनियर जाली की लंबाई है।

हम स्थानिक आवृत्ति की अवधारणा के माध्यम से एक विद्युत चुम्बकीय तरंग के आगमन के कोण को फिर से परिभाषित करते हैं:

$\ mu_R = \ frac {2 \ pi} {\ lambda} \ Delta sin (\ theta_R) = \ frac {2 \ pi} {\ lambda} \ Delta \ frac {\ lambda} {\ Delta M} = \ frac { 2 \ pi} {M}$

जहाँ $\ mu_R$ - बीम के मुख्य लोब की एक मानक चौड़ाई है ( मानक बीमोज़र )।

यह जाँचने के लिए कि हमारी पद्धति कितनी प्रभावी है और किन परिस्थितियों में, हम कोणीय पृथक्करण के लिए कुछ दिए गए मान प्रस्तुत करते हैं:

$\ mu_1 = - \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = \ mu_R \ quad$ - एक बीम चौड़ाई में विभाजन;
$\ mu_1 = -0.5 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0.5 \ mu_R \ quad$ - एक दूसरे बीम चौड़ाई में विभाजन;
$\ mu_1 = -0.3 \ mu_R, \ quad \ mu_2 = 0, \ quad \ mu_3 = 0.3 \ mu_R \ quad$ - बीम चौड़ाई के तीन दसवें भाग में विभाजन।

इनपुट मापदंडों को परिभाषित करें:

 M = 10 #    () SNR = 10 #  - (dB) d = 3 #     N = 50 #  "" (snapshots) S = ( np.sign(np.random.randn(d,N)) + 1j * np.sign(np.random.randn(d,N)) ) / np.sqrt(2) # QPSK W = ( np.random.randn(M,N) + 1j * np.random.randn(M,N) ) / np.sqrt(2) * 10**(-SNR/20) # AWGN #  : # sqrt(N0/2)*(G1 + jG2), #  G1  G2 -   . # .. Es( )  QPSK  1 ,    (noise spectral density): # N0 = (Es/N)^(-1) = SNR^(-1) [] (   ,  SNR = Es/N0); #    : # SNR_dB = 10log10(SNR) => N0_dB = -10log10(SNR) = -SNR_dB []; #    SNR    (..  ),   : # SNR = 10^(SNR_dB/10) => sqrt(N0) = (10^(-SNR_dB/10))^(1/2) = 10^(-SNR_dB/20) mu_R = 2*np.pi / M

विधि के बारे में थोड़ा सा सिद्धांत

सबसे पहले, हम ध्यान दें कि संगीत विधि के पूर्वज पिसारेंको विधि (1973) है। पिसरेंको विधि की मानी गई समस्या सफेद शोर में जटिल घातांक के योग की आवृत्तियों का अनुमान लगाना था। वी। एफ। पिसारेंको ने दिखाया कि आवृत्तियों को ऑटोकॉरेलेशन मैट्रिक्स के न्यूनतम आइगेनवैल्यू के अनुरूप ईजेनवेक्टरों से पाया जा सकता है। इसके बाद, यह विधि संगीत विधि का एक विशेष मामला बन गया। [२, पृ। 459]

श्मिट और उनके सहयोगियों ने 1979 [4] में मल्टीपल सिग्नल क्लासिफ़िकेशन अल्गोरिथम (संगीत) प्रस्तावित किया। इस एल्गोरिथ्म का मुख्य दृष्टिकोण प्राप्त सिग्नल के सहसंयोजक मैट्रिक्स को eigenvalues में विघटित करना है। चूंकि यह एल्गोरिदम असंबद्ध शोर को ध्यान में रखता है, इसलिए उत्पन्न कोवरियन मैट्रिक्स का विकर्ण रूप है। यहां, संकेत और शोर उप-स्थान की गणना रैखिक बीजगणित का उपयोग करके की जाती है, और एक दूसरे के लिए ऑर्थोगोनल हैं। इसलिए, एल्गोरिथ्म सिग्नल और नॉइज़ सबस्पेस को निकालने के लिए ऑर्थोगोनलिटी प्रॉपर्टी का उपयोग करता है [5]।

सामान्यीकृत संगीत एल्गोरिथ्म को इस प्रकार परिभाषित किया जा सकता है:

सहसंयोजक मैट्रिक्स का पता लगाएं $\ mathbf {R} _ {xx}$
ईवीडी या किसी अन्य उपयुक्त संख्यात्मक एल्गोरिथ्म के माध्यम से आइजनवेक्टर खोजें:

$\ mathbf {R} _ {xx} = \ mathbf {U} \ mathbf {\ Lambda} \ mathbf {U} ^ H \ qquad (1)$

छद्म वर्णक्रम ज्ञात करें (उपसर्ग छद्म के साथ क्यों, हम नीचे चर्चा करेंगे) निम्नलिखित सूत्र के माध्यम से संगीत:

$P_ {MU} (e ^ {j \ omega}) = \ frac {1} {\ _ \ _ limit_ {i = d + 1} ^ {M} | \ mathbf {a} ^ H \ mathbf (u) _i | ^ 2} \ qquad (2)$

जहाँ $\ mathbf {a} = \ _ {bmatrix} e ^ {j0 \ omega} & e ^ {j1 \ omega} & e ^ {j2 \ omega} & ... & e ^ {j (M-1) \ _ ओमेगा } \ end {bmatrix} ^ टी$ एक सीमा में पड़ी आवृत्ति the के लिए घातांक का वेक्टर है, और $\ mathbf {u} _i$ - i-th eigenvector (eigen वेक्टर) सहसंयोजक मैट्रिक्स (1) मैट्रिक्स के शोर उप-वर्ग के लिए इसी (1) - इसलिए के साथ अनुक्रमण $घ + १$ ( $घ$ मैट्रिक्स की रैंक (1)) है।

अधिक स्पष्टता के लिए, संदर्भ द्वारा प्रदान की गई उपयुक्त MATLAB स्क्रिप्ट को चलाने का प्रयास करें। दो मुख्य बिंदुओं पर ध्यान दें:
हर (2) में दूसरे मानदंड के वर्ग की गणना करने के बजाय, लेखक एफएफटी एल्गोरिथ्म को आइजनवेक्टरों पर लागू करते हैं, जो निर्मित कार्यों का उपयोग करके मॉडलिंग की सुविधा देता है और सामान्य रूप से, गणितीय दृष्टिकोण से सिद्धांत का खंडन नहीं करता है;
सहसंयोजक मैट्रिक्स को अवक्षेप मैट्रिक्स के माध्यम से गणना की जाती है; स्थानिक आवृत्तियों का अनुमान लगाने के लिए एक अलग दृष्टिकोण ऊपर दिखाया गया था।

जैसा कि आप नाम से अनुमान लगा सकते हैं, उच्च रिज़ॉल्यूशन के साथ स्वागत की दिशा का अनुमान लगाने के लिए MUSIC भी एक क्लासिक तरीका है। इस संदर्भ में छद्म स्पेक्ट्रा की गणना के लिए एल्गोरिथ्म नीचे दिया गया है:

हम प्राप्त संकेत के सहसंयोजक मैट्रिक्स पाते हैं;
शून्य उप-स्थान ढूंढें $\ mathbf {U} _0$ :

$\ mathbf {U} = [\ mathbf {U} _s \ quad \ mathbf {U} _0]$

कुछ खोज रेंज चुनें:

$a (\ mu) = \ start {bmatrix} e ^ {j0 \ mu_1} & ... & e ^ {j0 \ mu_Q} \\ ... & ... और ... \\ e ^ {j ( M-1) \ mu_1} और ... & e ^ {j (M-1) \ mu_Q} \ end {mmatrix}}$

जहाँ $\ mu = - \ frac {2 \ pi f_c} {c} \ Delta sin \ theta = - \ frac {2 \ pi} {\ lambda} \ Delta sin \ theta$

छद्म वर्णक्रम की गणना करें:

$P_ {MU} (\ theta) = \ frac {\ mathbf {a} ^ H (\ theta) \ mathbf {a} ((theta)} {\ mathbf {a} ^ H (\ theta) \ mathbf {U} _0 \ mathbf {U} _0 ^ H \ mathbf {a} (\ theta)}$

वर्णक्रमीय विश्लेषण और EM तरंगों के आगमन के कोण (DoA - दिशा की दिशा) के विश्लेषण के बीच संबंध तालिका 1 में वर्णित है।

सारणी अनुप्रयोगों के बीच तालिका 1 संचार : सिग्नल सरणी प्रसंस्करण और हार्मोनिक खोज [6]।

परिवर्तनशील	सिग्नल ऐरे प्रोसेसिंग	हार्मोनिक खोज
$एम$	सेंसरों की संख्या	समयावधि की संख्या
$एन$	समयावधि की संख्या	प्रयोगों की संख्या
$घ$	तरंग मोर्चों की संख्या	जटिल घटकों की संख्या
$\ _ मु$	स्थानिक आवृत्तियों	सामान्यीकृत आवृत्तियों

सामान्य तौर पर, ऐरे (झंझरी) के माध्यम से प्राप्त करने की प्रक्रिया की तुलना शास्त्रीय विवेक की प्रक्रिया से की जा सकती है, क्योंकि वास्तव में, प्रत्येक सेंसर, एक निश्चित चरण देरी के साथ एक लहर प्राप्त करता है (यानी, एक निश्चित समय देरी के साथ), एक नमूना डेल्टा पल्स के कार्यों को करता है। शास्त्रीय वर्णक्रमीय विश्लेषण की वास्तविकताओं (प्रयोगों) की संख्या समय खंडों (स्नैपशॉट) की संख्या के अनुरूप होगी। प्रत्येक स्रोत का अपना तरंग-प्रवाह होगा, जो वर्णक्रमीय विश्लेषण के मामले में संकेत के अद्वितीय साइनसोइड्स की संख्या के बराबर है।

और अब वापस eigenvectors की गणना के क्षण में। हमने पहले ही ऊपर उल्लेख किया है कि वैक्टर $a (\ theta_i) \ epsilon A$ जहाँ $i = 1,2, .., डी$ सहसंयोजक मैट्रिक्स के शोर उप-क्षेत्र के लिए ऑर्थोगोनल हैं, अर्थात:

$a ((theta_i) ^ TU_0 = 0 ^ T$

दरअसल, हम समीकरणों की एक प्रणाली देखते हैं, जिसे हल करके हम जड़ों को खोज सकते हैं - आइजनवेक्टर। इस तरह की विधि, संख्यात्मक एल्गोरिदम के विपरीत (जिससे, जैसा कि हमने ऊपर उल्लेख किया है, ईवीडी पर लागू होता है), एक व्यक्ति को अनुमानित ईजेनवल के बजाय वास्तविक प्राप्त करने की अनुमति देता है। यही कारण है कि यह दृष्टिकोण हमें एक सूडोस्पेक्ट्रम नहीं, बल्कि एक स्पेक्ट्रम प्राप्त करने की अनुमति देता है। इसी विचार ने रूट म्यूजिक एल्गोरिथम का आधार बनाया।

मोडलिंग

Fuf! अंत में, सभी सूत्र वर्णित हैं और कुछ हद तक समझाया गया है। हम मॉडलिंग शुरू कर सकते हैं।

 cases = [[-1., 0, 1.], [-0.5, 0, 0.5], [-0.3, 0, 0.3],] for idxm, c in enumerate(cases): #   ( ): mu_1 = c[0]*mu_R mu_2 = c[1]*mu_R mu_3 = c[2]*mu_R #   a_1 = np.exp(1j*mu_1*np.arange(M)) a_2 = np.exp(1j*mu_2*np.arange(M)) a_3 = np.exp(1j*mu_3*np.arange(M)) A = (np.array([a_1, a_2, a_3])).T #    X = np.dot(A,S) + W #    R = np.dot(X,np.matrix(X).H) U, Sigma, Vh = np.linalg.svd(X, full_matrices=True) U_0 = U[:,d:] #   thetas = np.arange(-90,91)*(np.pi/180) #   mus = np.pi*np.sin(thetas) #    a = np.empty((M, len(thetas)), dtype = complex) for idx, mu in enumerate(mus): a[:,idx] = np.exp(1j*mu*np.arange(M)) # MVDR: S_MVDR = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MVDR[idx] = 1 / (np.dot(np.matrix(a_idx).H, np.dot(np.linalg.pinv(R),a_idx))) # MUSIC: S_MUSIC = np.empty(len(thetas), dtype = complex) for idx in range(np.shape(a)[1]): a_idx = (a[:, idx]).reshape((M, 1)) S_MUSIC[idx] = np.dot(np.matrix(a_idx).H,a_idx)\ / (np.dot(np.matrix(a_idx).H, np.dot(U_0,np.dot(np.matrix(U_0).H,a_idx)))) plt.subplots(figsize=(10, 5), dpi=150) plt.semilogy(thetas*(180/np.pi), np.real( (S_MVDR / max(S_MVDR))), color='green', label='MVDR') plt.semilogy(thetas*(180/np.pi), np.real((S_MUSIC/ max(S_MUSIC))), color='red', label='MUSIC') plt.grid(color='r', linestyle='-', linewidth=0.2) plt.xlabel('Azimuth angles θ (degrees)') plt.ylabel('Power (pseudo)spectrum (normalized)') plt.legend() plt.title('Case #'+str(idxm+1)) plt.show()

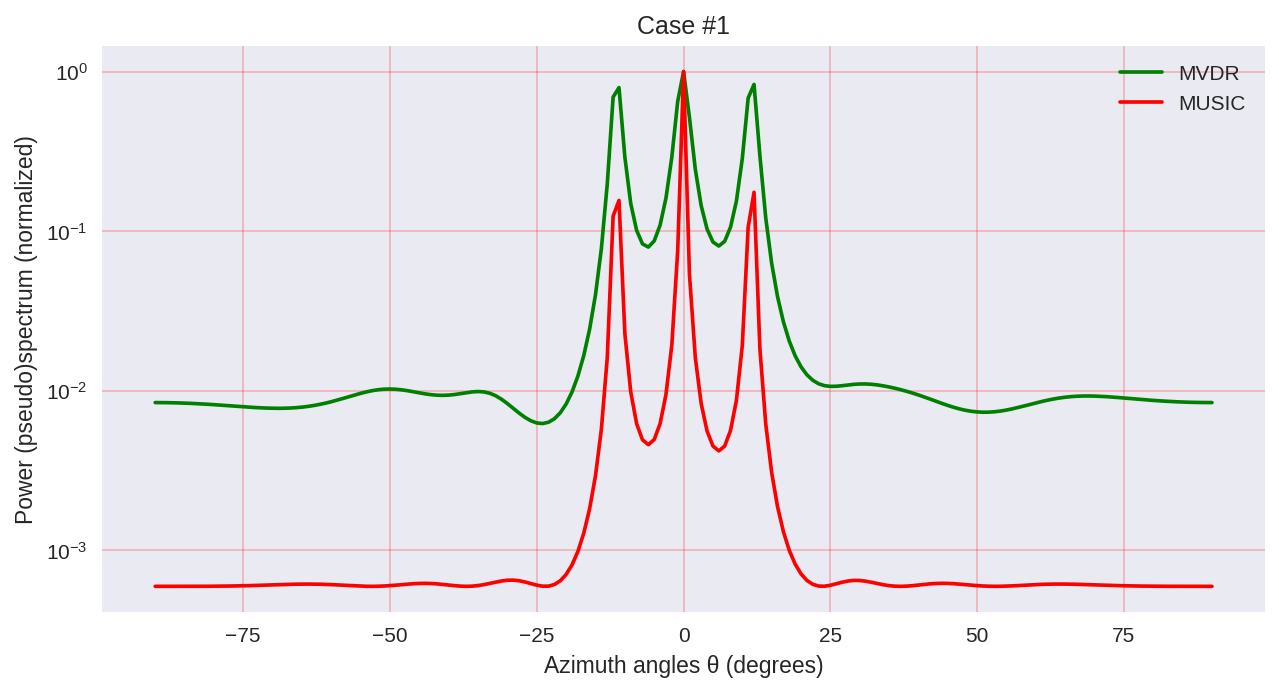
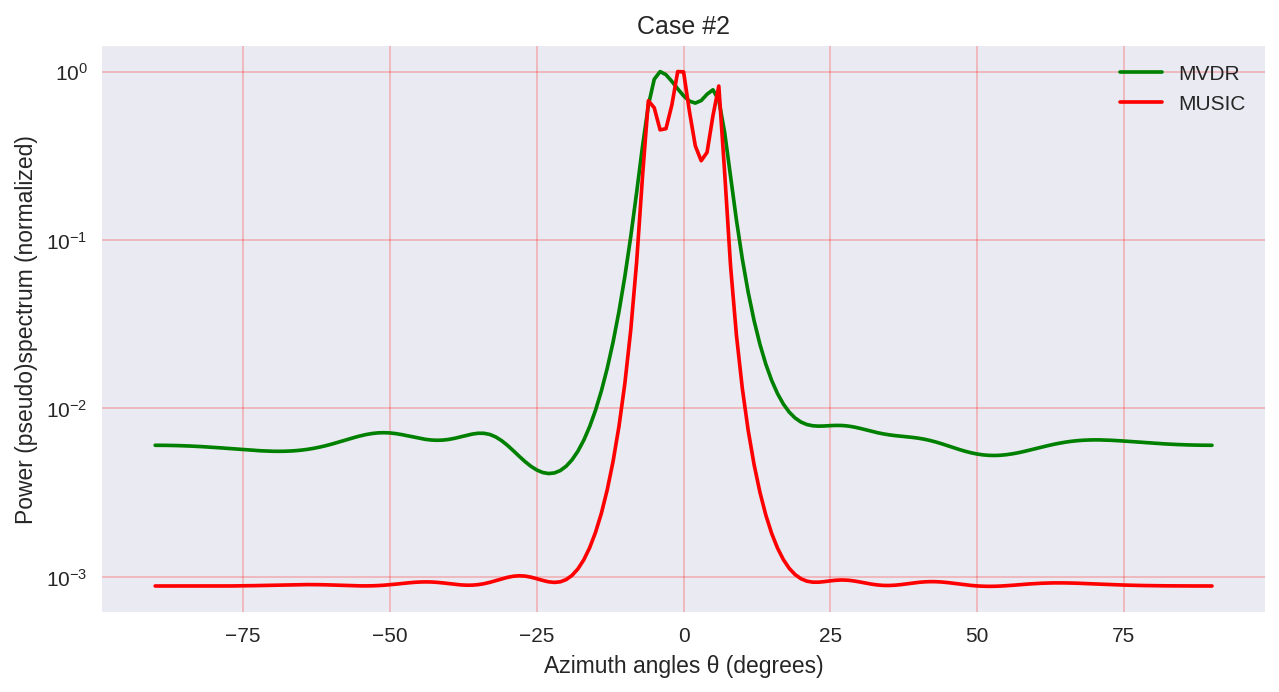
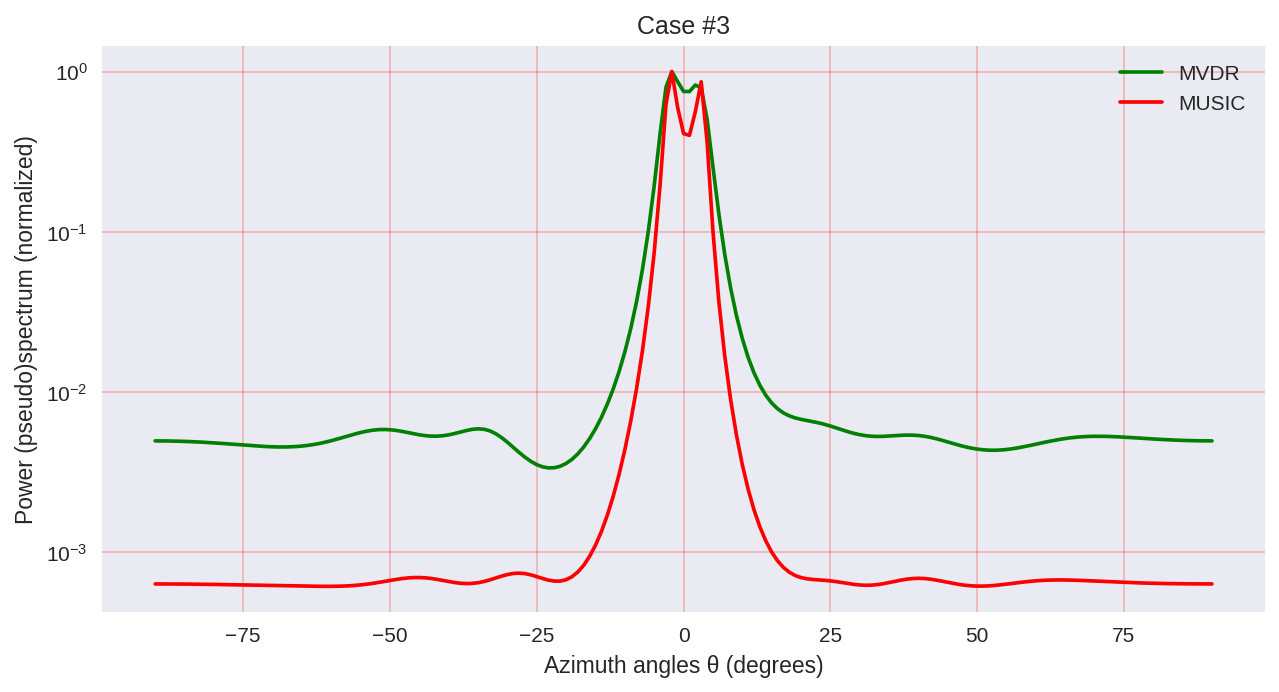
जैसा कि हम देख सकते हैं, संगीत का एक उच्च रिज़ॉल्यूशन है और सामान्य रूप से बेहतर परिणाम प्राप्त करने की अनुमति देता है, उदाहरण के लिए, एमवीडीआर अनुमति देता है - वर्णक्रमीय विश्लेषण के पैरामीट्रिक तरीकों का एक ही प्रतिनिधि।

हालांकि, यह ध्यान में रखा जाना चाहिए कि संगीत का उपयोग करते समय हम अधिक कम्प्यूटेशनल रूप से महंगे एल्गोरिदम का उपयोग करते हैं, जैसे कि ईवीडी या एसवीडी, जो अधिक सटीकता के लिए कुछ कीमत पर है।

ऐसी बातें।

प्रयुक्त साहित्य की सूची:

हेकिन, साइमन और केजे रे लियू। सरणी प्रसंस्करण और सेंसर नेटवर्क पर हैंडबुक। वॉल्यूम। 63. जॉन विले एंड संस, 2010. पीपी। 102-107
हेस एमएच सांख्यिकीय डिजिटल सिग्नल प्रोसेसिंग और मॉडलिंग। - जॉन विले एंड संस, 2009।
हेकिन, साइमन एस। एडेप्टिव फिल्टर सिद्धांत। पियर्सन एजुकेशन इंडिया, 2008. पीपी। 422-427
रिचमंड, क्राइस्ट डी। "कैपोन एल्गोरिदम का अर्थ है-चुकता त्रुटि सीमा SNR भविष्यवाणी और संकल्प की संभावना।" सिग्नल प्रोसेसिंग पर IEEE लेनदेन 53.8 (2005): 2748-2764।
एसकेपी गुप्ता, संगीत और बेहतर संगीत एल्गोरिथ्म के आगमन की भयावहता के लिए, IEEE, 2015।
प्रोफेसर मार्टिन हैअर्ड के व्याख्यान ( एरे सरणी )

हम एक विद्युत चुम्बकीय तरंग के आगमन की दिशा निर्धारित करने के लिए MUSIC एल्गोरिथ्म का मॉडल बनाते हैं