सभी को शुभ दिन!
स्थानिक विविधता के विषय पर विचार करते हुए, हम पहले से ही संचार चैनलों में लुप्त होती के मुद्दों पर और इस तरह के लुप्त होती क्यों है पर छुआ है। आज मैं इस विषय पर थोड़ा और विस्तार से बात करने का प्रस्ताव करता हूं।
इसके अलावा, आज के लेख में हम MIMO चैनलों के स्थानिक सहसंबंध के मुद्दों पर थोड़ा स्पर्श करेंगे, जो परंपरागत रूप से प्रोफेसर हाडर्ट के मोबाइल संचार ( CSP ) पाठ्यक्रम के दौरान निपटाए जाते हैं, और इसलिए, मेरी राय में, इस तरह का प्रकाशन अतिश्योक्तिपूर्ण नहीं होगा। और, मैं अभी ध्यान देता हूं, मुद्दों की श्रेणी केवल मोबाइल संचार में उपयोग करने के लिए सीमित नहीं है।
सामान्य तौर पर, मैं वायरलेस संचार के विषय में रुचि रखने वालों को पढ़ने के लिए आमंत्रित करता हूं, और चलें!
कॉलिन स्लेटर "लुप्त होती यादें" । हां, एक विषय में सब कुछ कम करने के लिए संभवतः ओवरकिल है, लेकिन कुछ ऐसे रूपक के साथ, मुझे लगता है कि आप कल्पना कर सकते हैं कि मूल, सूचना संकेत पर सभी प्रकार के प्रभावों के बाद रिसीवर को क्या प्राप्त होता है ...
हम किस बारे में बात कर रहे हैं?
आइए इस तथ्य से शुरू करें कि प्रकृति में तथाकथित गुणात्मक शोर हैं जो प्राप्त संकेत शक्ति को प्रभावित करते हैं - लुप्त होती ।
जैसा कि आपने अनुमान लगाया है, रूसी और अंग्रेजी में सीधे अनुवाद नहीं किया जाता है, लेकिन यह बहुत महत्वपूर्ण नहीं है।अंग्रेजी साहित्य में, लुप्त होती शब्द का एक निश्चित प्रभाव होता है, जो कि जैसा था, हमारे संकेत को "फीका" करने का कारण बनता है।
हमारे साहित्य में, लुप्त होती शब्द का उपयोग आमतौर पर किया जाता है, और यह मुख्य रूप से बहुपथ प्रभाव के कारण होता है: यदि एक विद्युत चुम्बकीय तरंग परावर्तन और विवर्तन द्वारा उत्पन्न अपनी प्रतिलिपि का सामना करती है, और वे एंटीपेज़ में हैं, तो लहरें एक दूसरे को रद्द कर देंगी - अर्थात, चैनल , जैसा कि यह था, जमा देता है ।
लुप्त होती तेज और धीमी ( तेजी से और धीमी गति से लुप्त होती) है।
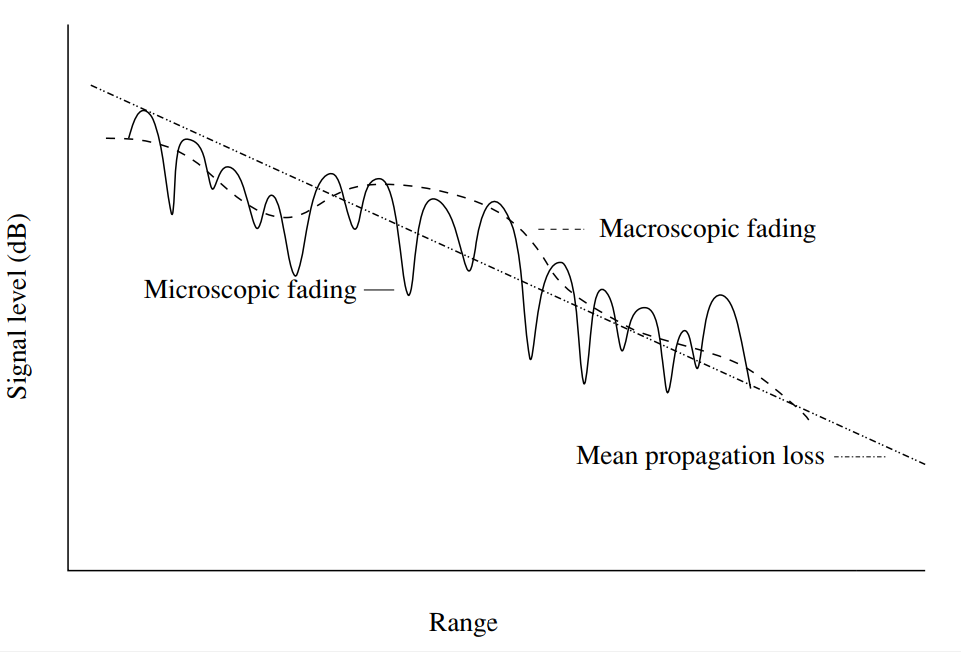
अंजीर। 1. दूरी के आधार पर वायरलेस चैनलों में सिग्नल पावर में उतार-चढ़ाव। बढ़ते स्तर के साथ प्रचार नुकसान का औसत स्तर नीरस रूप से बढ़ता है। मैक्रोस्कोपिक (धीमी) और सूक्ष्म (तेज) लुप्त होती [1, पी। 15] के कारण स्थानीय विचलन हो सकता है।
मैं तुरंत स्वीकार करता हूं, आज हम धीमे लुप्त होने के साथ काम नहीं करेंगे, लेकिन हम तेजी से पर्याप्त विस्तार से बात करेंगे।

अंजीर। 2. छायांकन प्रभाव का चित्रण: एक नियम के रूप में, छायांकन (शेडिंग) के कारण धीमी गति से लुप्त होती है। अनुकरण के लिए, लॉगनॉर्मल वितरण आमतौर पर चुना जाता है।
यदि आप धीमी गति से लुप्त होती के बारे में थोड़ा पढ़ना चाहते हैं, विशेष रूप से, और आप कैसे सैटेलाइट चैनलों का अनुकरण कर सकते हैं, सामान्य तौर पर, मैं आपको यहां आमंत्रित करता हूं!
तेजी से लुप्त होती
तेजी से लुप्त होती, एक नियम के रूप में, दो मुख्य कारणों से होता है:
- बहु प्रचार के कारण हम पहले ही उल्लेख कर चुके हैं और / या
- डॉपलर आवृत्ति बदलाव के कारण।
उत्तरार्द्ध उपग्रह प्रणालियों के लिए बहुत ही ध्यान देने योग्य हैं, लेकिन हमेशा स्थलीय संचार के मामलों को ध्यान में नहीं रखा जाता है, इस तथ्य के कारण कि इस मामले में बेस स्टेशन, एक नियम के रूप में, स्थिर हैं।

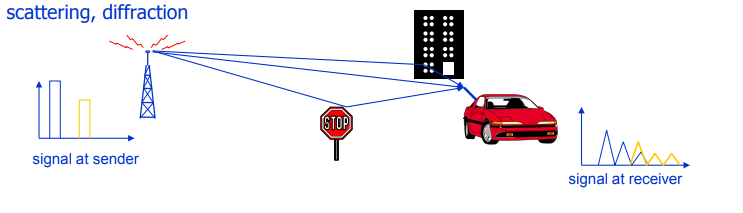
अंजीर। 3. लुप्त होती के कारणों का चित्रण। बिखरने और विवर्तन पर विशेष ध्यान दिया जाता है: यह इन घटनाओं के कारण ठीक है कि तथाकथित बहुपथ प्रसार का गठन होता है, जिससे इंटरसिंबल हस्तक्षेप ( आईएसआई ) होता है।
लेकिन वह सब से बहुत दूर है।
चयनात्मक लुप्त होती बनाम सपाट लुप्त होती
ऊपर, हमने घटना की प्रकृति द्वारा हमारे हस्तक्षेप को विभाजित किया। हालांकि, हस्तांतरित संकेत पर प्रभाव की प्रकृति द्वारा हस्तक्षेप को भी विभाजित किया जा सकता है। और यहां हमें चैनल चयनात्मकता की अवधारणा की आवश्यकता है।
हम [1, पी के अनुसार एक छोटा वर्गीकरण देते हैं। 14-18]। तो, तेजी से लुप्त होती जा सकता है:
- चुनिंदा (चयनात्मक)
एक। फ़्रिक्वेंसी चयनात्मक
ख। चुनिंदा समय-डोमेन (समय चयनात्मक)
में। स्थानिक रूप से चयनात्मक (यह ईएम तरंगों के आगमन और प्रस्थान के कोण के मुद्दे से संबंधित है - आज हम इस लक्ष्य का विश्लेषण नहीं करेंगे) - फ्लैट - धीमी गति से लुप्त होती की प्रकृति की ओर अधिक ध्यान देना (हाँ, यह इस तरह का विरोधाभास है)
अंतिम शब्द का तात्पर्य विपरीत से समझाया गया है।
सबसे पहले, यदि हमारे द्वारा प्रेषित सिग्नल के स्पेक्ट्रम की चौड़ाई चैनल के सुसंगत बैंडविड्थ से अधिक है, तो वे कहते हैं कि हम आवृत्ति-चयनात्मक हस्तक्षेप से निपट रहे हैं।
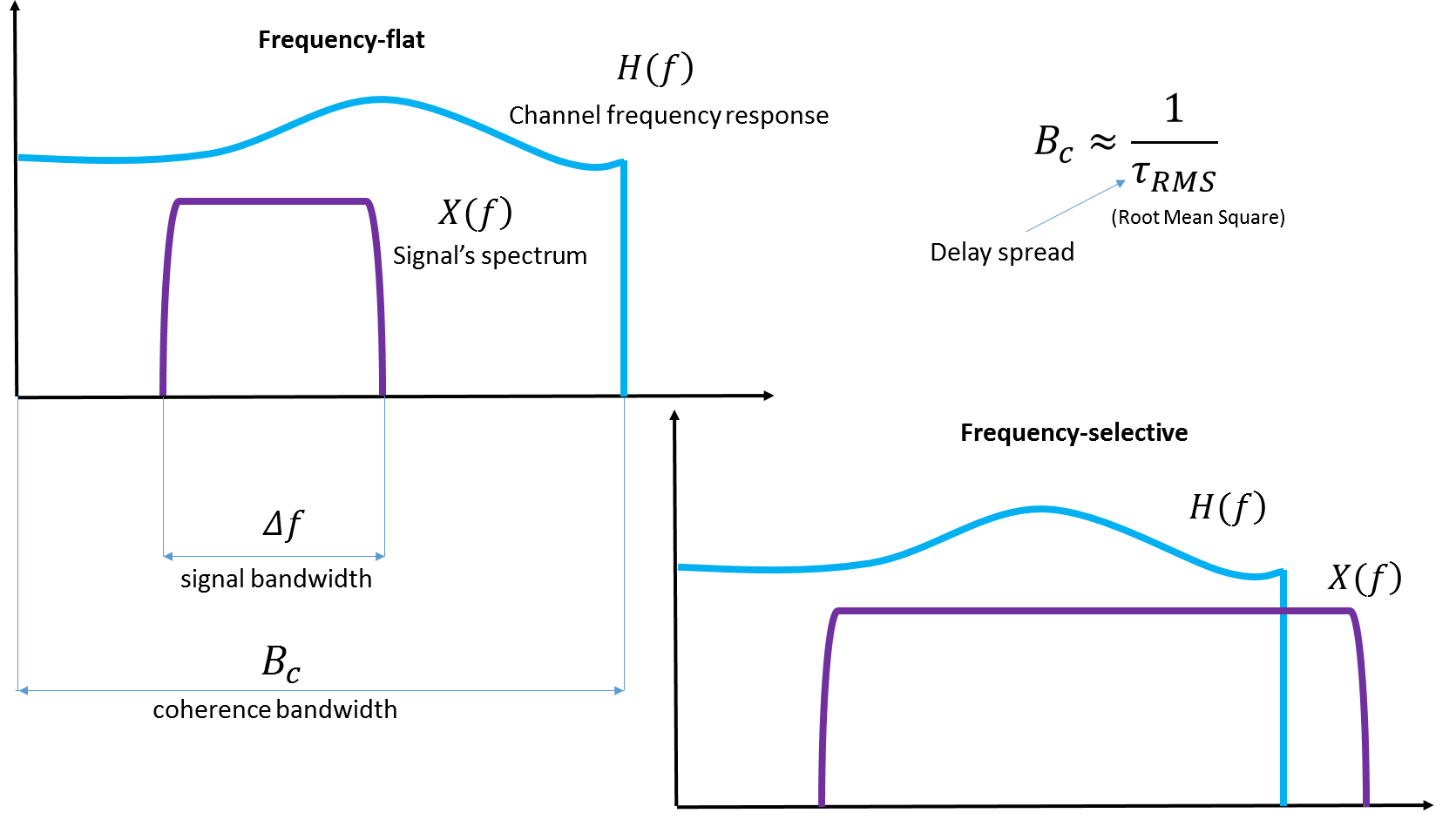
अंजीर। 4. सुसंगत बैंडविड्थ का चित्रण। मुझे लगता है कि विकी से इलस्ट्रेशन अटैच करना बुरा नहीं होगा, अगर वह खुद उन्हें वहां जोड़ ले।
देरी का प्रसार चर पर ध्यान दें - देरी का प्रसार । यह एक ही संकेत की विभिन्न प्रतियों के आगमन के बीच देरी में फैलता है जो किसी विशेष वास्तविक चैनल की विशेषताओं को निर्धारित करने पर मापा जाता है।
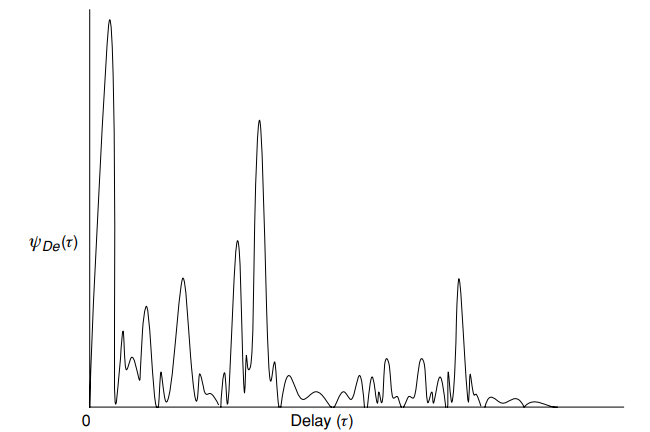
अंजीर। 5. विशिष्ट देरी (शक्ति) प्रोफ़ाइल ) - देरी के एक समारोह के रूप में औसत शक्ति
- देरी के एक समारोह के रूप में औसत शक्ति  । [१, पी 16]
। [१, पी 16]
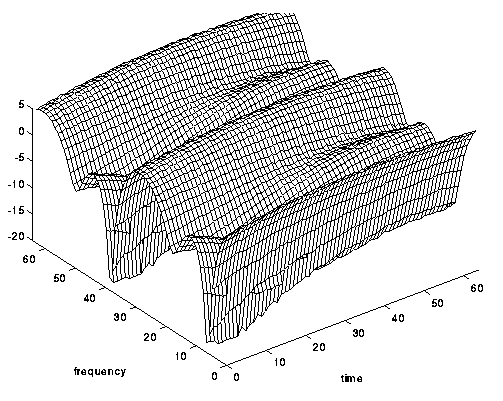
अंजीर। 6. आवृत्ति-चयनात्मक, लेकिन समय-चयनात्मक चैनल नहीं ।
प्रत्येक सीमा के लिए, सुसंगत बैंड अलग होगा।उदाहरण के लिए, एस-बैंड के लिए (मुझे तब दिलचस्पी थी जब मैं सैटेलाइट सिस्टम की जानकारी खोज रहा था) Bc = 0.5 - 2 MHz (कनाटस एजी, पनागोपोलोस AD (एड।)। रेडियो वेव प्रोगैशन एंड चैनल मॉडलिंग ऑन अर्थ - स्पेस सिस्टम्स। - CRC प्रेस, 2016 । - पी। 107)।
उदाहरण के लिए, इस तरह के एक उपग्रह ट्रान्सीवर के बॉड दर पर यह बहुत अच्छी तरह से फिट बैठता है। और कुछ भी आश्चर्य की बात नहीं है: डिजिटल मॉड्यूलेशन (PSK, QAM, OFDM) के रेखीय प्रकार का प्रतीक दर संकेत के कब्जे वाले बैंड के साथ मेल खाता है ( गोल्डस्मिथ ए वायरलेस संचार देखें । - स्टैनफोर्ड यूनिवर्सिटी, 2004. - पी। 140, 326)। यह अधिकतम करने के लिए सुसंगत बैंड में संकेत निचोड़ने की कोशिश करना अच्छा होगा। फ़्रीक्वेंसी अभी भी एक मूल्यवान संसाधन हैं।
दूसरे, यदि समय डोमेन में हमारे सिग्नल की लंबाई चैनल के सुसंगतता समय से अधिक है , तो वे कहते हैं कि हम एक चैनल के साथ काम कर रहे हैं जो समय में भिन्न होता है।
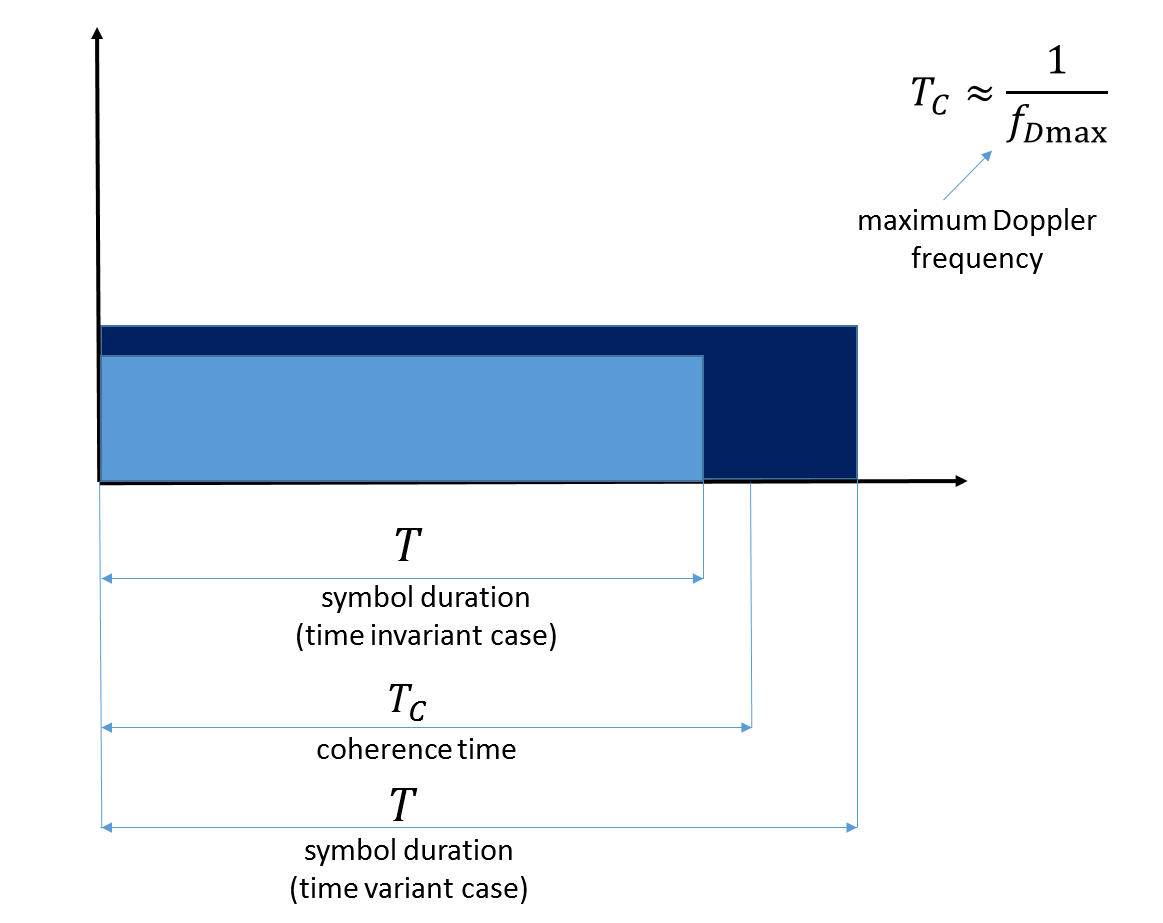
अंजीर। 7. सुसंगति समय का चित्रण। कृपया ध्यान दें कि यहां अधिकतम डॉपलर आवृत्ति स्वयं मोबाइल टर्मिनल के आंदोलन को दर्शाती है।
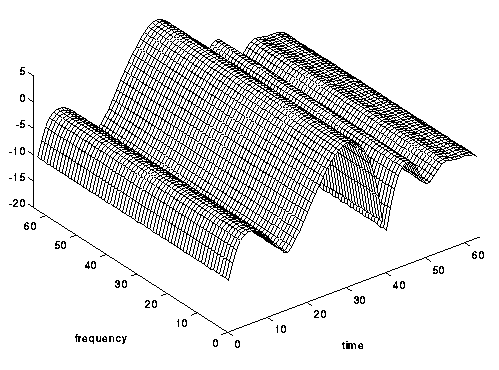
अंजीर। 8. लगभग समय-अदृश्य, लेकिन समय-चयनात्मक: एक तेजी से क्षय चैनल।
वास्तविक जीवन में, दुर्भाग्य से, दोनों को उम्मीद करनी चाहिए। ठीक है, और तदनुसार, अगर हम किसी भी तरह से ऊपर से बचने का प्रबंधन करते हैं, तो हम सबसे सरल और सबसे सुविधाजनक मामले में आएंगे - फ्लैट लुप्त होती [1, पी। 14-18] [2, पी। 88-92]।
सबसे आसान लुप्त होती चैनल
आपने पहले ही एक फ्लैट चैनल का अनुकरण करने का एक समान तरीका देखा होगा जिसमें कहीं भी लुप्त होती है:
h = (1/sqrt(2))*(randn(size(msg)) + 1j*randn(size(msg)))
क्या मतलब है:
- दृष्टि की कमी (स्थलीय संचार के लिए उचित मामला)
- संकीर्ण चैनल (संकीर्ण चैनल) - सुसंगत बैंड में फिट होता है
- कोई आवृत्ति चयनात्मकता नहीं है - सुसंगत समय में फिट
- छायांकन और डॉपलर आवृत्ति पारियों की कमी
यही है, यहां यह व्यक्ति में है: लुप्त होती के साथ एक फ्लैट चैनल । दृष्टि की रेखा के बिना एक मामले के लिए, चैनल को रेले भी कहा जाता है।

लॉर्ड रेले
ऐसे मॉडल से क्या आता है?
सबसे पहले, आधुनिक संचार प्रणालियों के बारे में बोलते हुए, हम सबसे अधिक संभावना है कि डिजिटल सिग्नल के साथ काम कर रहे हैं। इसके अलावा, हम चतुर्थांश प्रकार के मॉड्यूलेशन ( I / Q ) के साथ भी काम कर रहे हैं, यानी जटिल संकेतों के साथ।

अंजीर। 9. सिग्नल नक्षत्र QPSK । ध्रुवीय निर्देशांक, इकाई चक्र। उदाहरण के लिए, प्रतीक 11 लगभग 0.7 + 0.7i के बराबर एक समन्वय के अनुरूप होगा ।
वास्तविक और काल्पनिक दोनों घटकों पर हस्तक्षेप के प्रभाव को मानना तर्कसंगत है। इसके अलावा, यह केंद्रीय सीमा प्रमेय का अनुसरण करने के लायक है, ताकि इस तरह के प्रभावों की गॉसियन प्रकृति को भी मान सकें। हम सूत्र [1, पी लिखते हैं। 39]:
जहाँ ) और
और ) सामान्य रूप से यादृच्छिक चर वितरित किए जाते हैं।
सामान्य रूप से यादृच्छिक चर वितरित किए जाते हैं।
सबसे अधिक, सामान्यीकृत औसत शक्ति वाले मॉडल का उपयोग किया जाता है:
और इसका मतलब है ) ।
।
यदि हम सिग्नल लिफाफे के घटकों की स्वतंत्र विकृतियों को मानते हैं: दोनों में ( I - इन-फेज) और क्वाड्रिचर ( Q - क्वाडरेचर), तो उस संख्या की स्थिति जिसके द्वारा मूल चिन्ह को गुणा किया जाएगा (इसलिए गुणक शोर), ध्रुवीय निर्देशांक में हो सकते हैं पाइथागोरस प्रमेय द्वारा शाब्दिक गणना:
जहाँ ) और
और ) - ये भी आम तौर पर यादृच्छिक चर वितरित किए जाते हैं। रेटेड शक्ति के लिए
- ये भी आम तौर पर यादृच्छिक चर वितरित किए जाते हैं। रेटेड शक्ति के लिए ) ।
। ) ।
।
और यहाँ हम Rayleigh प्रक्रिया का सूत्र है ! [२, पृष्ठ 78 2]
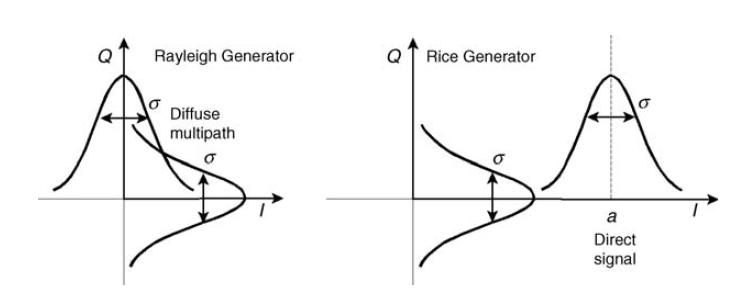
अंजीर। 10. गॉल्सियन ने रेले और राइस फ़ेडिंग के लिए जेनरेटरों को चौंका दिया [3, p.125]। हम थोड़ी देर बाद राइस चैनल के बारे में बात करेंगे।
गीतात्मक विषयांतर।व्यक्तिगत रूप से, मैं वास्तव में तोप की शूटिंग के साथ उदाहरण को पसंद करता हूं: यदि दो बंदूकें एक-दूसरे को पर्याप्त समय तक लंबवत गोली मारती हैं, तो व्यक्तिगत रूप से प्रत्येक के लिए हिट का वितरण सामान्य होगा, और हिट का कुल वितरण रेले है। हमारे हस्तक्षेप से कुछ ऐसा ही हो रहा है।
यदि हम चैनलों के बीच किसी स्थानिक संबंध के बिना सबसे सरल मामले पर विचार करते हैं (मान लें कि हमारे पास कई स्थानिक चैनल हैं - MIMO ), तो वे कहते हैं कि चैनल स्थानिक रूप से सफेद है - स्थानिक रूप से सफेद । और चूंकि सभी चैनल स्वतंत्र हैं, इसलिए, रेले के अनुसार न केवल यादृच्छिक चर वितरित करना संभव है, बल्कि वैक्टर, मैट्रीस, और टेंसर [3, पी। 125] भी हैं।
जहाँ %20) और
और %20) क्या सामान्य रूप से वितरित मूल्यों से मेल खाते हैं।
क्या सामान्य रूप से वितरित मूल्यों से मेल खाते हैं।
1/2 जड़ के नीचे कहां से आया?यहां सब कुछ काफी सरल है: जैसा कि हमने ऊपर कहा, चैनल की प्रतिक्रिया शक्ति एकता के बराबर होनी चाहिए, अर्थात्:
यह इसके लिए है कि स्केलिंग कारक पेश किया जाता है  ।
।
प्रदर्शित करें (एक परिवर्तन के लिए अजगर को लें):
import numpy as np N = int(1e6) h = 1/np.sqrt(2)*(np.random.randn(N) + 1j*np.random.randn(N)) P = np.mean(h*np.conj(h)) print(np.round(P)) >>> (1+0j)
संक्षेप में :
प्रत्यक्ष दृश्यता की अनुपस्थिति में हस्तक्षेप घटक को एन-आयामी वेक्टर (चैनल आयाम के आधार पर) के रूप में परिपत्र समरूपता और शून्य चटाई के साथ जटिल गाऊसी कानून के अनुसार स्वतंत्र रूप से वितरित ( आईआईडी - स्वतंत्र रूप से वितरित) के रूप में वर्णित किया जा सकता है। अपेक्षा ( ZMCSCG - शून्य-मतलब गोलाकार सममित जटिल गाऊसी) संख्या।
एक पूरी जीभ ट्विस्टर!
लगभग सबसे आसान लुप्त होती चैनल
ठीक है, क्या होगा अगर अभी भी प्रत्यक्ष दृश्यता है? हो सकता है कि इस स्कोर पर पहले से तैयार गणितीय मॉडल मौजूद हों?
बेशक वहाँ है! उदाहरण के लिए, यह [4] , कई प्राप्त करने और प्रसारित करने वाले एंटेना (MIMO) के मामले के लिए सामान्यीकृत:
जहाँ  - यह वास्तव में चैनल (या चैनल मैट्रिक्स, अगर हम MIMO के बारे में बात कर रहे हैं) के आवेग प्रतिक्रिया का जटिल लिफाफा है,
- यह वास्तव में चैनल (या चैनल मैट्रिक्स, अगर हम MIMO के बारे में बात कर रहे हैं) के आवेग प्रतिक्रिया का जटिल लिफाफा है,  प्रत्यक्ष दृश्यता (लाइन-ऑफ-साइट) का एक घटक है, और
प्रत्यक्ष दृश्यता (लाइन-ऑफ-साइट) का एक घटक है, और  - यह प्रत्यक्ष दृश्यता (नॉन-लाइन-ऑफ-साइट) की कमी का एक घटक है, हम पहले ही इस पर विचार कर चुके हैं।
- यह प्रत्यक्ष दृश्यता (नॉन-लाइन-ऑफ-साइट) की कमी का एक घटक है, हम पहले ही इस पर विचार कर चुके हैं।
चर K पर ध्यान दें - यह तथाकथित रिकियन फैक्टर (Rian / Ricean factor) है - अन्य सभी रास्तों की शक्ति के लिए सीधे प्रसार पथ की शक्ति का अनुपात। यह वह है जो निर्धारित करता है कि हमारा चैनल हस्तक्षेप के अधीन कितना होगा।

स्टीफन ओ। "स्टीव" राइस
रक़म  चैनल मैट्रिक्स की गणितीय अपेक्षा का प्रतिनिधित्व करता है और एंटेना के प्राप्त और संचारण सरणियों की ज्यामिति के आधार पर मॉडल किया जा सकता है:
चैनल मैट्रिक्स की गणितीय अपेक्षा का प्रतिनिधित्व करता है और एंटेना के प्राप्त और संचारण सरणियों की ज्यामिति के आधार पर मॉडल किया जा सकता है:
जहाँ ) और
और ) - ये क्रमशः, और, एंटेना के सरणियों को प्राप्त करने और प्रसारित करने की प्रतिक्रियाएं हैं
- ये क्रमशः, और, एंटेना के सरणियों को प्राप्त करने और प्रसारित करने की प्रतिक्रियाएं हैं  और
और  आगमन और प्रस्थान के कोण हैं (प्रस्थान के कोण)।
आगमन और प्रस्थान के कोण हैं (प्रस्थान के कोण)।
कारक आमतौर पर सममित होते हैं और सामान्य सूत्र द्वारा वर्णित किए जा सकते हैं:
जहाँ  एंटेना (ऐन्टेना रिक्ति) के बीच की दूरी तरंग दैर्ध्य में है, और
एंटेना (ऐन्टेना रिक्ति) के बीच की दूरी तरंग दैर्ध्य में है, और  - यह एंटेना के सरणी में तत्वों की संख्या है (छवि 11)।
- यह एंटेना के सरणी में तत्वों की संख्या है (छवि 11)।
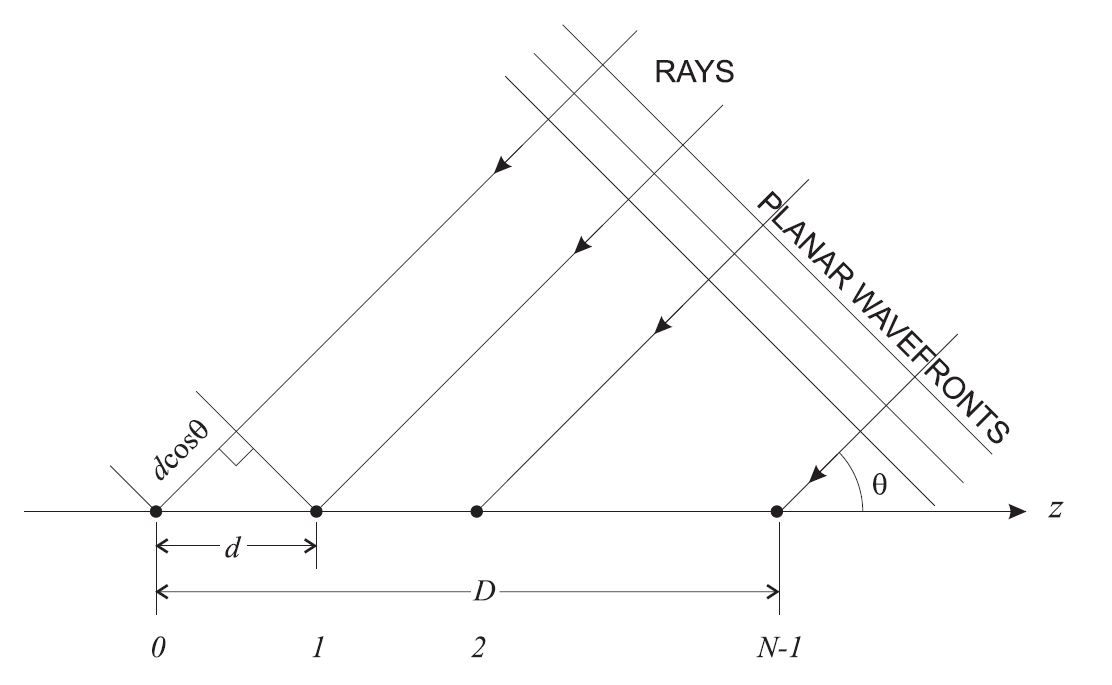
अंजीर। 11. एक रेखीय सरणी की ज्यामिति । बड़े पैमाने पर MIMO के लिए, ज्यामिति, निश्चित रूप से, अलग होगी। आप इसके बारे में अधिक पढ़ सकते हैं, उदाहरण के लिए, यहां ।
खैर, अब जब मॉडल कम से कम कुछ हद तक असंतुष्ट है, तो आप इसे सरल कर सकते हैं।
SISO (सबसे सरल और सबसे बुनियादी) के मामले के लिए, सूत्र (5) फॉर्म लेगा:
1 संचारण और 1 प्राप्त करने वाले एंटीना के लिए %5Cmathbf%7Ba%7D_R(%5Ctheta_R)%20%3D%201) ।
।
और यह, चित्र 12 में मॉडल को फिट बैठता है।
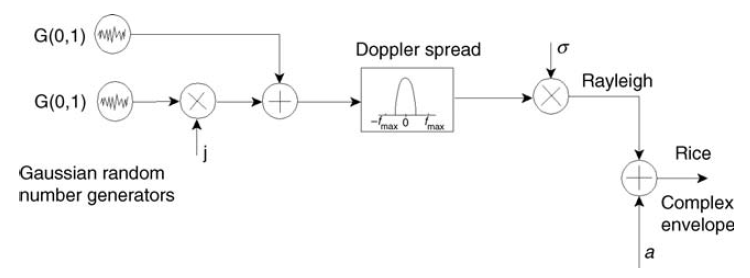
अंजीर। 12. राइस चैनल (संकरी संकेत) के निर्माण की योजना [3, पृष्ठ .27]। पर  चैनल Rayleigh में अधिक से अधिक पतित होगा। इसीलिए मैंने लगभग सबटाइटल में इस शब्द का इस्तेमाल किया: रेले चैनल राइस चैनल का एक विशेष मामला है। इसे सूत्र (5) से भी देखा जाता है।
चैनल Rayleigh में अधिक से अधिक पतित होगा। इसीलिए मैंने लगभग सबटाइटल में इस शब्द का इस्तेमाल किया: रेले चैनल राइस चैनल का एक विशेष मामला है। इसे सूत्र (5) से भी देखा जाता है।
आइए हम बताते हैं: %7D%7D) रशियन स्केल पैरामीटर है, और
रशियन स्केल पैरामीटर है, और  एक गैर-केंद्रितता पैरामीटर है।
एक गैर-केंद्रितता पैरामीटर है।
यदि हम फ्लैट लुप्त होती पर विचार करते हैं, तो यह माना जाता है कि डॉपलर स्प्रेड ब्लॉक में 1 की प्रतिक्रिया है।सामान्य तौर पर, डॉपलर स्प्रेड को मॉडलिंग करने के उद्देश्य से , सबसे अधिक संभावना है कि आप सम-साइनसोइड्स तकनीक के आधार पर एक जेक मॉडल (यू-आकार) में आएंगे। सैद्धांतिक रूप से, ऐसे मॉडल का स्पेक्ट्रम इस तरह दिखता है:

10 हर्ट्ज की अधिकतम डॉपलर पारी के साथ रेलेघेन क्षीणन की शक्ति वर्णक्रमीय घनत्व। स्रोत ।
हालांकि, जीवन में, [1, पी। 15] ऐसा स्पेक्ट्रम अभी भी कम दिखता है:
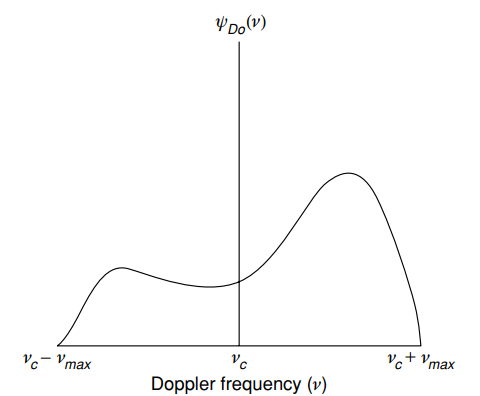
विशिष्ट डॉपलर (ऊर्जा) स्पेक्ट्रम ) - डॉपलर आवृत्ति के एक समारोह के रूप में औसत शक्ति
- डॉपलर आवृत्ति के एक समारोह के रूप में औसत शक्ति ) [१, पृ। 15]।
[१, पृ। 15]।
उम्मीदें ... वास्तविकता।
धीमी लुप्त होती के साथ संयोजन के लिए ऐसी योजनाएं हैं।उदाहरण के लिए, यह कोराज़ा-वतालारो मॉडल (C & V) के लिए है :
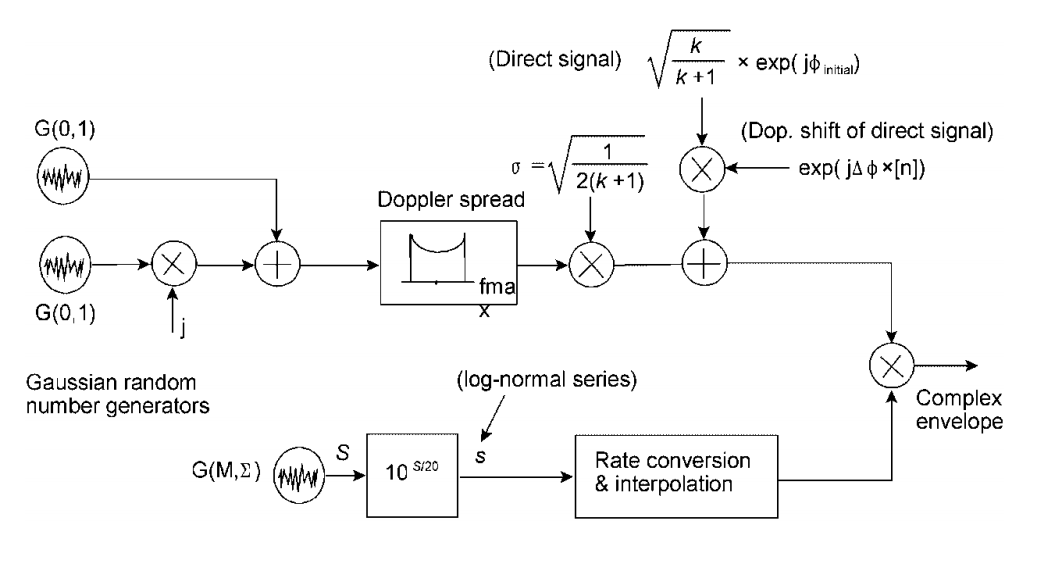
फॉन्टन, एफपी, मेयो, ए।, मरोट, डी।, प्रेटो - सेर्डेइरा, आर।, मारीनो, पी।, मचाडो, एफ।, और रिएरा, एन। (2008) देखें। नैरोबैंड लैंड मोबाइल उपग्रह प्रसार चैनल के लिए जेनरेटर मॉडल की समीक्षा। इंटरनेशनल जर्नल ऑफ़ सैटेलाइट कम्युनिकेशंस एंड नेटवर्किंग, 26 (4), 291-316।
लेकिन यह पूरी तरह से अलग कहानी है ...
मतलाब में लगभग सबसे आसान लुप्त होती चैनल मॉडलिंग
आइए पहले से जाँच की गई चीज़ के साथ प्राप्त गणनाओं की तुलना करें। उदाहरण के लिए, विशेष माटलाब कार्यों के साथ ।
मॉडल का परीक्षण करने के लिए, हमारे भाग के लिए, हम एक यादृच्छिक बाइनरी संदेश (संदेश की लंबाई 100,000 बिट्स) उत्पन्न करते हैं, एम-पीएसके या एम-क्यूएएम का उपयोग करके इसे संशोधित करते हैं, लुप्त होती प्रक्रिया को तत्व से गुणा करते हैं, सफेद गाऊसी शोर जोड़ते हैं, शून्य-मजबूर तुल्यकारक को बराबर करते हैं, डिमोड्यूलेट और गणना करते हैं। बिट त्रुटि अनुपात (BER - बिट त्रुटि अनुपात) (छवि 13)। परीक्षणों की संख्या एक सौ के बराबर होगी।
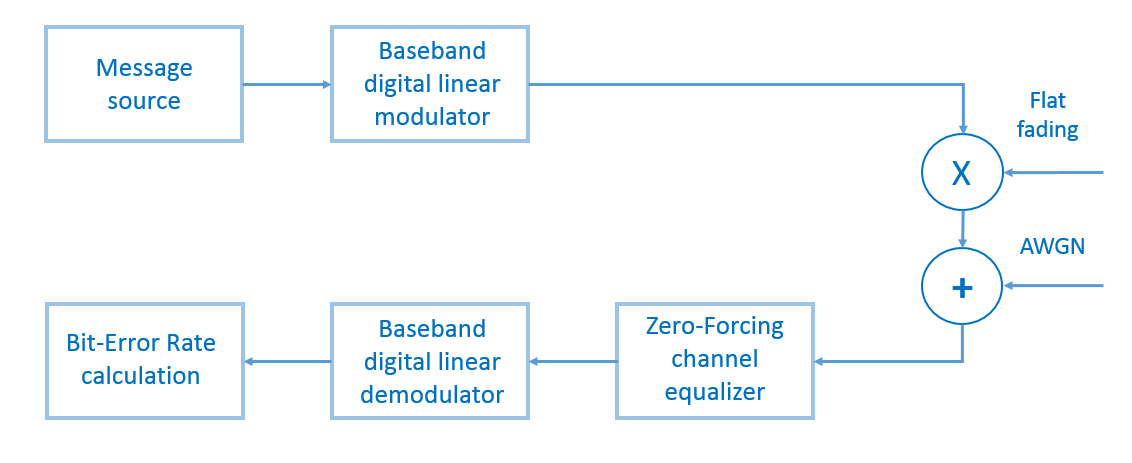
चित्र 13। ट्रांसमिशन सिस्टम के मॉडल का ब्लॉक आरेख जिसे हमारी स्क्रिप्ट वर्णित करेगी।
स्क्रिप्ट को यहां देखा जा सकता है।और यहाँ डाउनलोड करें ।
clear all; close all; clc EbNo = 0:40; K = [4.0; 0.6]; M = [4; 8; 16; 64; 256];
आपको कुछ इस तरह से मिलना चाहिए:
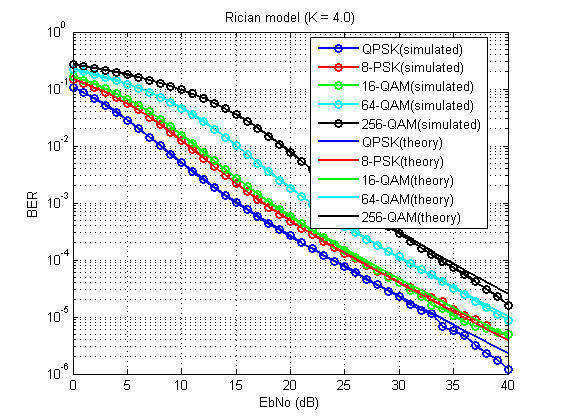
अंजीर। 14. माना मॉडल (K = 4.0) के लिए बिट त्रुटियों का गुणांक।
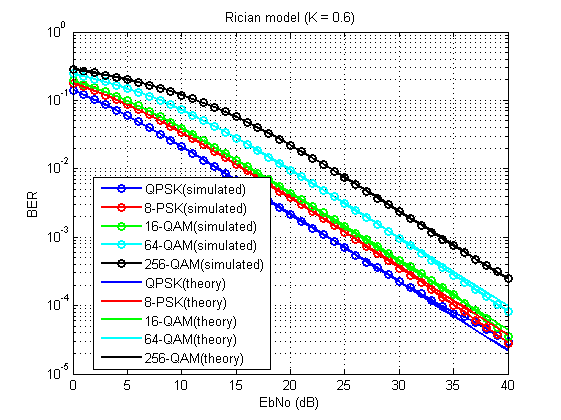
अंजीर। 15. माना मॉडल के लिए बिट त्रुटि दर (K = 0.6)।
दोषों के बिना, निश्चित रूप से (औसत संख्या की सीमित संख्या के कारण), लेकिन सामान्य तौर पर, यह देखा जा सकता है कि यह काम करता है!
ठीक है, लेकिन क्या मिमो के मामले में प्रयोग को स्केल करना संभव होगा? हां बिल्कुल।ऐसा करने के लिए, हम एक धारणा बनाते हैं: चैनल मैट्रिक्स में स्वतंत्र प्रसार पथ शामिल होंगे, जिनमें से प्रत्येक को चावल के अनुसार वितरित किया जाएगा।
यह किन परिस्थितियों में संभव है?
जैसा कि हमने ऊपर उल्लेख किया है, घटक IID को किसी भी आयाम में उत्पन्न किया जा सकता है। इसका मतलब यह है कि दृष्टि की रेखा के बिना किसी भी स्थानिक श्वेत MIMO चैनल को SISO चैनलों (चैनल आयाम के आधार पर) के एक सेट के रूप में मॉडलिंग की जा सकती है।
दृष्टि घटक की रेखा के साथ थोड़ा और अधिक जटिल - आपको झंझरी की स्थिति को ध्यान में रखना होगा।
सूत्र पर विचार करें (5): अगर दृष्टि घटक की हमारी मैट्रिक्स केवल इकाइयों से मिलकर बनेगी  , ऐसा लगता है कि रेयोसव घटक भी स्थानिक रूप से सफेद हो जाता है।
, ऐसा लगता है कि रेयोसव घटक भी स्थानिक रूप से सफेद हो जाता है।
इस तक पहुंचने के लिए, हम सूत्र (6) की तुलना में दृष्टि घटक की रेखा को अधिक विस्तार से लिखते हैं:
)%20%20%5C%5C%0A.%20%5C%5C%0A.%20%5C%5C%0A.%5C%5C%0A%5Cexp(j(M_R-1)2%5Cpi%20dcos(%5Ctheta_R))%0A%5Cend%7Bbmatrix%7D%20%5Cbegin%7Bbmatrix%7D%20%0A1%20%26%20%5Cexp(j2%5Cpi%20dcos(%5Ctheta_T))%20%20%26%20.%20%26%20.%20%26%20.%20%26%0A%5Cexp(j(M_T-1)2%5Cpi%20dcos(%5Ctheta_T))%0A%5Cend%7Bbmatrix%7D%0A)
यह हड़ताली है कि अगर  , तब मैट्रिक्स में एक इकाइयाँ शामिल होंगी। ज्यामितीय रूप से, यह एक ऐसी स्थिति है जब तत्वों के दो सरणियों को एक दूसरे पर कड़ाई से उन्मुख किया जाता है:
, तब मैट्रिक्स में एक इकाइयाँ शामिल होंगी। ज्यामितीय रूप से, यह एक ऐसी स्थिति है जब तत्वों के दो सरणियों को एक दूसरे पर कड़ाई से उन्मुख किया जाता है:
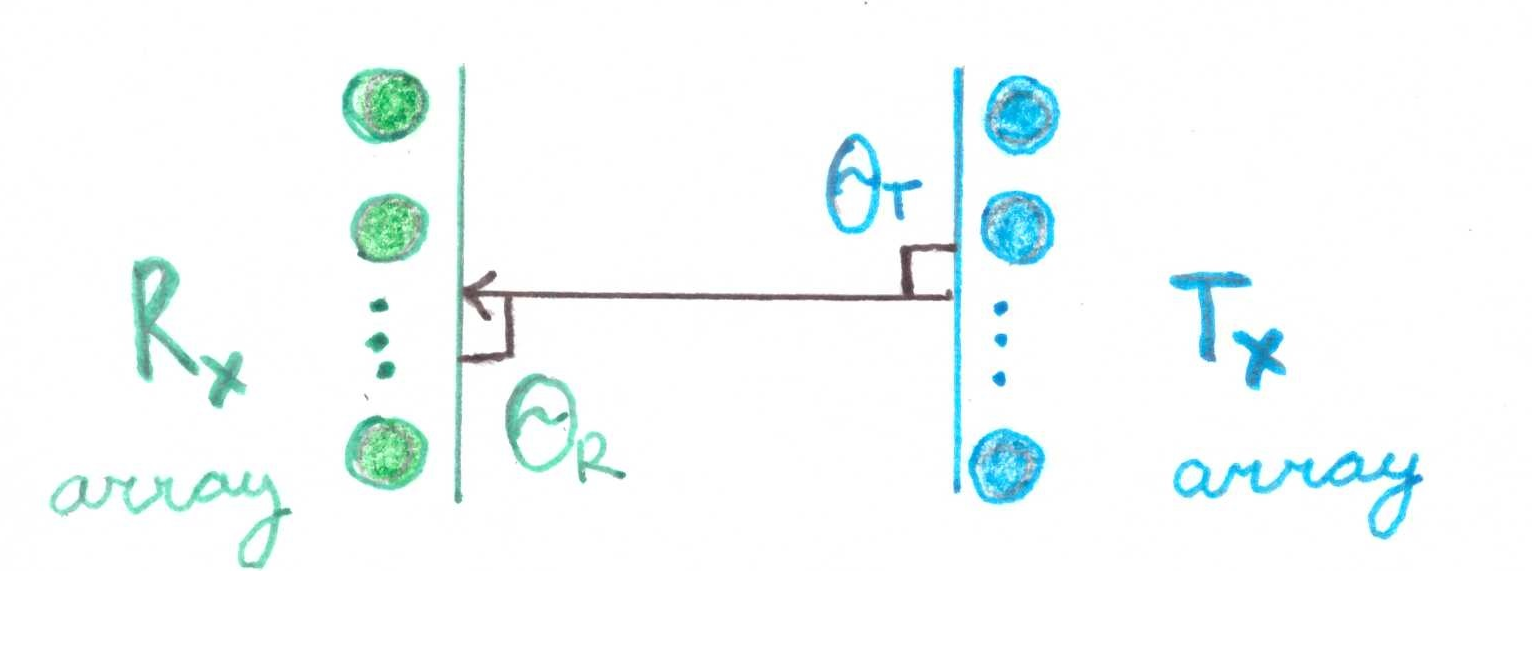
चलो थोड़ा गणित प्रदर्शन करते हैं:
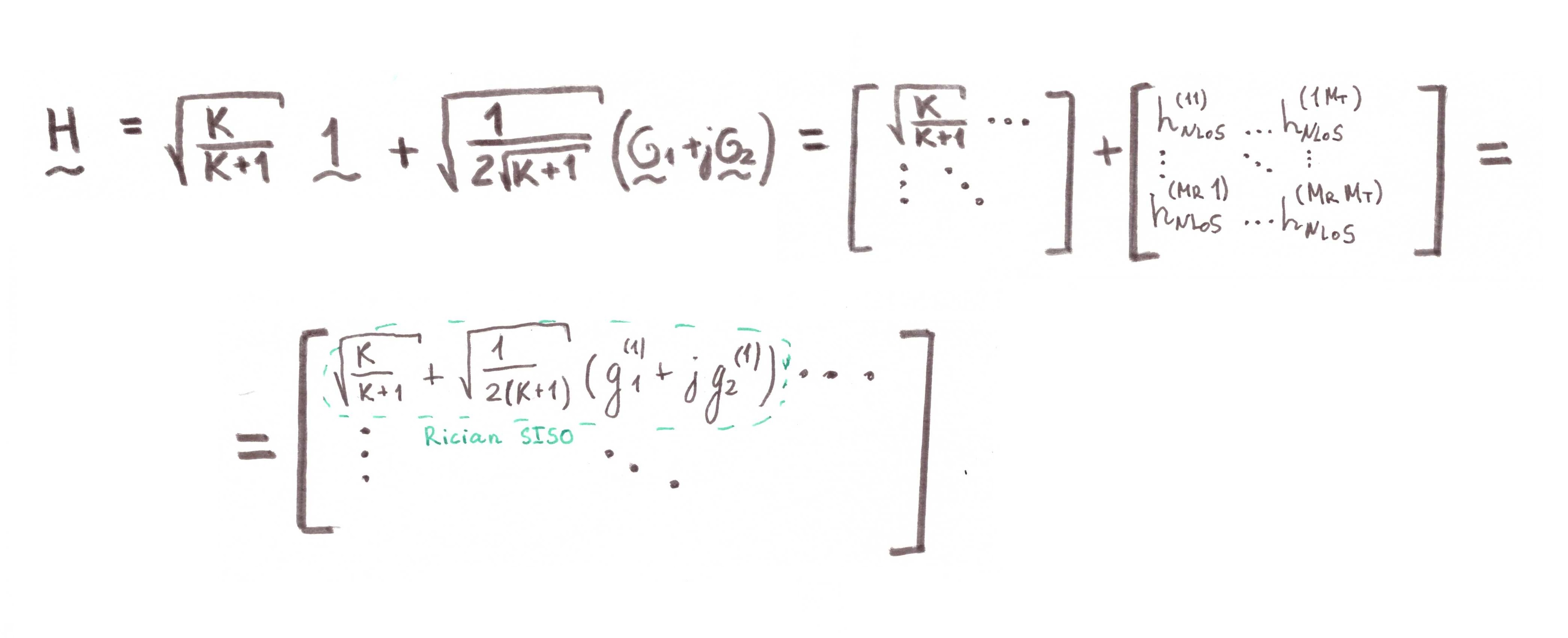
मॉडलिंग के लिए, हम आधार के रूप में आलमूटी योजना लेते हैं। यह कुछ इस तरह से बाहर करना चाहिए:
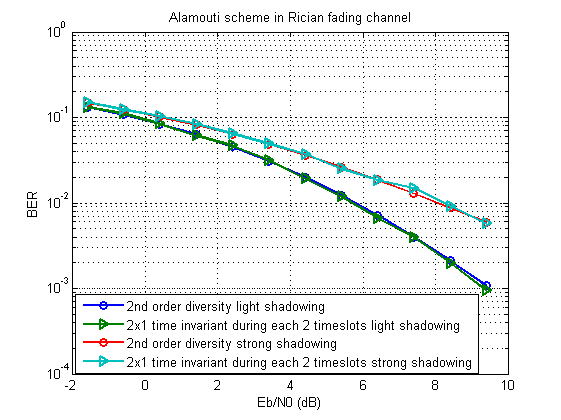
विस्तारित स्क्रिप्ट को यहां डाउनलोड किया जा सकता है ।
अच्छा किया।
लगभग सबसे आसान लुप्त होती चैनल और स्थानिक सहसंबंध
और अब, सांख्यिकीय गणनाओं की दुनिया में अपनी यात्रा पूरी करते हुए, आइए वास्तविकता के थोड़ा करीब पहुँचें।
ऊपर, हमने उस मामले पर विचार किया जब दृष्टि की रेखा की कमी का घटक स्थानिक रूप से सफेद था। हालांकि, वास्तविक प्रणालियों से किसी को अभी भी एंटेना के बीच कुछ सहसंबंध की उम्मीद करनी चाहिए, और इसलिए ईएम लहर के प्रसार मार्गों के बीच।
हम एक नया चर पेश करते हैं - स्थानिक सहसंबंध मैट्रिक्स:
जहाँ vec एक वैश्वीकरण ऑपरेशन को दर्शाता है। वैसे, यह मैट्रिक्स केवल दृष्टि की रेखा की कमी के घटक को प्रभावित करेगा, और इसलिए इस मामले में  ।
।
यह मानना उचित है कि वास्तविक जीवन में, यह मैट्रिक्स पहले माप के माध्यम से निर्धारित किया जाता है, और उसके बाद ही उन्हें मॉडलिंग के लिए उपयोग किया जाता है:
जहाँ  IID मैट्रिक्स है ( w का अर्थ है स्थानिक रूप से w hite)।
IID मैट्रिक्स है ( w का अर्थ है स्थानिक रूप से w hite)।
ध्यान दें कि एक मैट्रिक्स को एक शक्ति में ऊपर उठाना उसके प्रत्येक तत्व की शक्ति को बढ़ाने के लिए नहीं है। इसलिए, हमारे मामले में, MatLab में sqrt () फ़ंक्शन का उपयोग नहीं किया जा सकता है। ऑपरेटर का उपयोग करें ^ ।
पायथन के लिए, आप घातांक ** ऑपरेटर और लोकप्रिय खस्ता मॉड्यूल के sqrt विधि का उपयोग नहीं कर सकते। आपको scipy मॉड्यूल की भिन्नात्मक_मेट्रिक्स_पावर विधि का उपयोग करने की आवश्यकता है।
यदि रिसीवर और ट्रांसमीटर एक दूसरे से पर्याप्त रूप से स्वतंत्र हैं, जैसा कि चित्र 16 में है, तो क्रोनकर मॉडल को लागू किया जा सकता है [1, पी। 40], गणना के लिए गुणांक की संख्या को कम करने के लिए:
जहाँ  क्रोनर कार्य को दर्शाता है।
क्रोनर कार्य को दर्शाता है।

लियोपोल्ड क्रोनकर
हम अभिव्यक्ति मैट्रिक्स के घटकों पर अलग से विचार करते हैं:
%5ET%5Cright%5C%7D) प्राप्त एंटेना का सहसंबंध मैट्रिक्स है,
प्राप्त एंटेना का सहसंबंध मैट्रिक्स है,
 एंटेना संचारित करने का सहसंबंध मैट्रिक्स है
एंटेना संचारित करने का सहसंबंध मैट्रिक्स है
 और
और  - यह क्रमशः एंटेना प्राप्त करने और प्रसारित करने की संख्या है। दोनों मैट्रीज पॉजिटिव सेमीफाइनल हर्मिटियन मैट्रीस हैं। इसके अलावा, मैट्रिक्स की रैंक
- यह क्रमशः एंटेना प्राप्त करने और प्रसारित करने की संख्या है। दोनों मैट्रीज पॉजिटिव सेमीफाइनल हर्मिटियन मैट्रीस हैं। इसके अलावा, मैट्रिक्स की रैंक  मूल्य द्वारा सीमित
मूल्य द्वारा सीमित %2C%20rank(%5Cmathbf%7BR%7D_R))) ।
।

अंजीर। 16।
गैर-सहसंबंधी रिसीवर और ट्रांसमीटर के मामले में विसारक का मॉडल। ग्रीन डॉट्स का मतलब डिफ्यूज़र, ब्लू और रेड मीन रिसीवर और ट्रांसमीटर है। मैं गुणवत्ता के लिए माफी मांगता हूं, यह टीयू इलमानौ के होमवर्क में से एक का स्क्रीनशॉट है।
इस मामले में चैनल मैट्रिक्स को इस प्रकार लिखा जा सकता है:
हालांकि, जैसे स्थितियों के लिए, उदाहरण के लिए, चित्र 17 में, आपको अभी भी पूर्ण सहसंबंध मैट्रिक्स का उपयोग करना होगा (देखें सूत्र (9))।
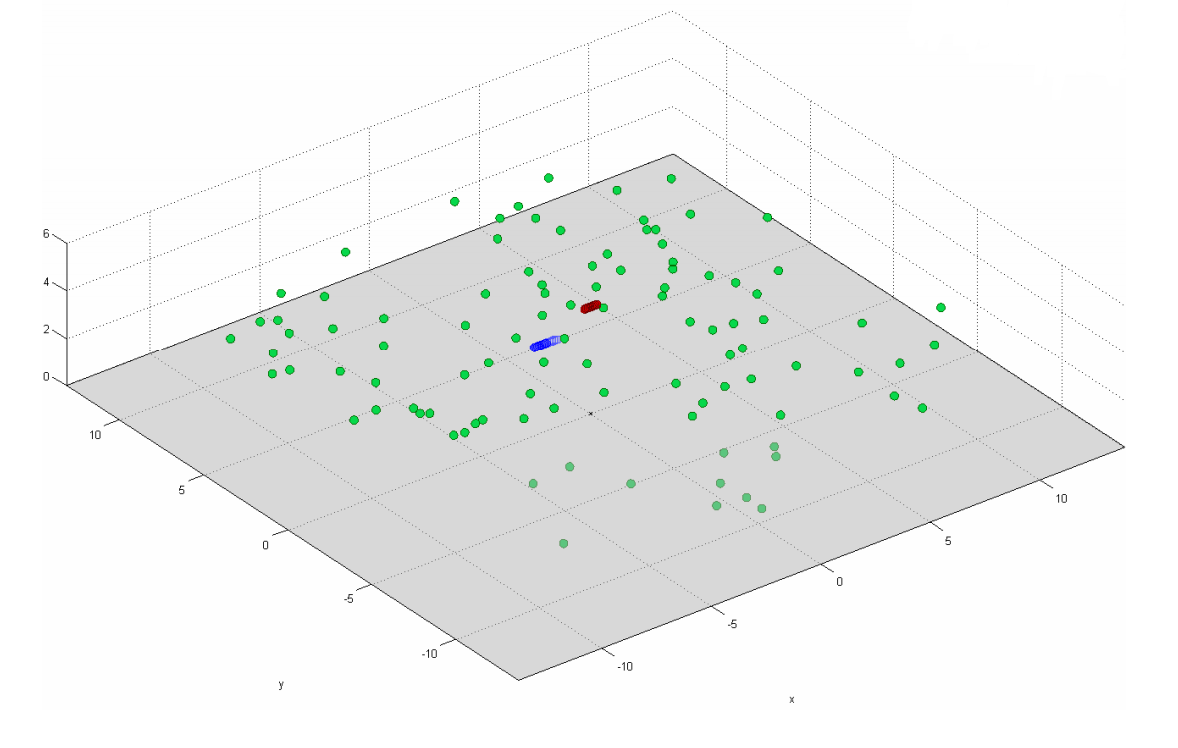
अंजीर। 17. सहसंबंधी रिसीवर और ट्रांसमीटर के मामले में डिफ्यूज़र का मॉडल। ग्रीन डॉट्स का मतलब डिफ्यूज़र, ब्लू और रेड मीन रिसीवर और ट्रांसमीटर है।
हमने जो कुछ सीखा है उसे समेकित करने और यह देखने के लिए कि कैसे स्थानिक सहसंबंध जीवन को जटिल बनाता है, चलो चैनलों की बैंडविड्थ की गणना करने का प्रयास करें। उदाहरण के लिए, MIMO 2x2 के लिए।
ऐसा करने के लिए, हम निम्नलिखित मामलों को लेते हैं (हमारा मतलब है कि सभी एक ही फ्लैट लुप्त होती हैं, सादगी के लिए हम केवल रेले चैनल पर भी विचार करते हैं:
1) स्थानिक रूप से सफेद चैनल;
2) एक अपेक्षाकृत कमजोर सहसंबंध के साथ क्रोनर मॉडल:
3) अपेक्षाकृत मजबूत सहसंबंध के साथ क्रोनकर मॉडल:
हम इस भाग में पायथन 3.4 का उपयोग करेंगे। बैंडविड्थ की गणना करने का कार्य मेरे पिछले प्रकाशनों में से एक से लिया जाएगा।
import numpy as np from numpy import linalg as LA import matplotlib.pyplot as plt from scipy.linalg import fractional_matrix_power def openloop_capacity(H_chan, SNR_dB): SNR = 10**(SNR_dB/10) Mt = np.shape(H_chan)[1] H_sq = np.dot(H_chan,np.matrix(H_chan, dtype=complex).H) lambdas = LA.eigvals(H_sq) lambdas = np.sort(lambdas)[::-1] c = 0 for eig in lambdas: c = c + np.log2(1 + SNR*eig/Mt) return np.real(c)
सिस्टम के मुख्य मापदंडों को परिभाषित करें:
Mr = 2
हम सिमुलेशन शुरू करते हैं:
counter = 1000 SNR_dBs = [i for i in range(1, 21)] C_MIMO_uncorr = np.empty((len(SNR_dBs), counter)) C_MIMO_kron1 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron2 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron3 = np.empty((len(SNR_dBs), counter)) C_MIMO_kron4 = np.empty((len(SNR_dBs), counter)) for c in range(counter): H_uncorr = (np.random.randn(Mr,Mt) + 1j*np.random.randn(Mr, Mt))/np.sqrt(2) H_kron1 = np.dot(Rr1_half, np.dot(H_uncorr, Rt1_half_H)) H_kron2 = np.dot(Rr2_half, np.dot(H_uncorr, Rt2_half_H)) for idx, SNR_dB in enumerate(SNR_dBs): C_MIMO_uncorr[idx, c] = openloop_capacity(H_uncorr, SNR_dB) C_MIMO_kron1[idx, c] = openloop_capacity(H_kron1, SNR_dB) C_MIMO_kron2[idx, c] = openloop_capacity(H_kron2, SNR_dB) C_MIMO_uncorr_erg = np.mean(C_MIMO_uncorr, axis=1) C_MIMO_kron1_erg = np.mean(C_MIMO_kron1, axis=1) C_MIMO_kron2_erg = np.mean(C_MIMO_kron2, axis=1)
ड्राइंग plt.figure(figsize=(7, 5), dpi=100) plt.plot(SNR_dBs, C_MIMO_uncorr_erg,'g-o', label='Uncorrelated') plt.plot(SNR_dBs, C_MIMO_kron1_erg, 'm-o', label='Kronecker model, case 1') plt.plot(SNR_dBs, C_MIMO_kron2_erg, 'r-o', label='Kronecker model, case 2') plt.title("Rayleigh flat fading (MIMO 2x2)") plt.xlabel('SNR (dB)') plt.ylabel('Ergodic capacity (bps/Hz)') plt.legend() plt.minorticks_on() plt.grid(which='major') plt.grid(which='minor', linestyle=':') plt.show()
हमें मिलता है:
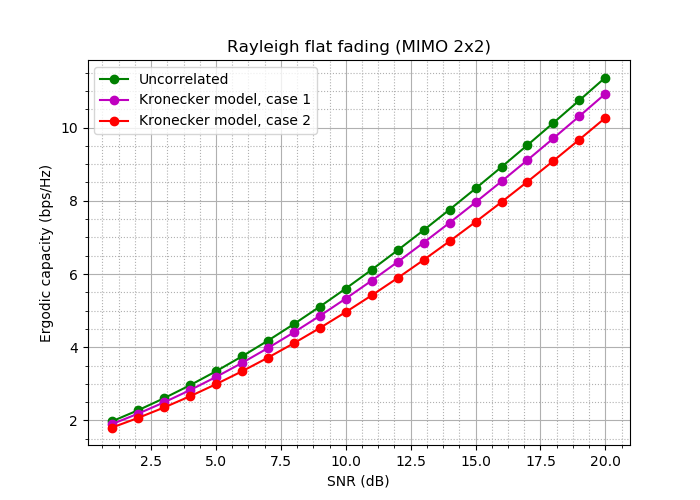
अंजीर। 18. इन प्रयोगों के लिए बैंडविड्थ घटता है।
ठीक है: अंतर, हालांकि महत्वपूर्ण नहीं है, है!
अंतभाषण
शायद पाठकों में से एक यह नोटिस कर सकता है कि हमने आज (विस्तार में और पासिंग में) लगभग हर चीज को बहुत अच्छी तरह से matlab ऑब्जेक्ट के मापदंडों पर टिकी हुई है। यह तथ्य मुझे बहुत महत्वपूर्ण लगता है:
- सबसे पहले, यह आगे वर्णित प्रणाली को व्यवस्थित करता है,
- और, दूसरी बात, यह इस बात पर बल देता है कि हम वर्तमान मुद्दों को संबोधित कर रहे हैं।
ठीक है, और अब, यदि आप ऐसे ब्लॉक का उपयोग करते हैं, तो, मुझे आशा है, यह अधिक स्पष्ट होगा कि आपको क्यों और किस पेन को मोड़ने की आवश्यकता है।
ध्यान देने के लिए आप सभी का धन्यवाद!
पुनश्च
मैं यहाँ रीनर एस। थॉमा ( इलमेनौ ) के विषय की स्लाइड्स का लिंक जोड़ूंगा , जिस पर उन्होंने उस समय हमें व्याख्यान दिया था। मुझे लगता है कि कोई काम आएगा!
साहित्य
- पॉलराज, आरोग्यस्वामी, रोहित नाबर, और धनंजय गोर। स्पेस-टाइम वायरलेस संचार का परिचय। कैम्ब्रिज यूनिवर्सिटी प्रेस, 2003।
- गोल्डस्मिथ ए। वायरलेस संचार। - कैम्ब्रिज यूनिवर्सिटी प्रेस, 2005।
- Fontn, फर्नांडो Pærez, और Perfecto Mari Espo Espiiraeira। वायरलेस प्रसार चैनल मॉडलिंग: Matlab के साथ एक सिमुलेशन दृष्टिकोण। वॉल्यूम। 5. जॉन विली एंड संस, 2008।
- फ़ारोखी, फ़ारोख आर।, एट अल। "एफडीएमए / टीडीएमए वायरलेस सिस्टम की वर्णक्रमीय दक्षता संचारित होती है और एंटीना सरण प्राप्त करती है।" वायरलेस संचार 1.4 (2002) पर IEEE लेनदेन: 591-599।