परिचय
परियोजना के बारे में
परियोजना
"निरपेक्ष विनिमय दर" युग्मित विनिमय दरों के विश्लेषण में लगी हुई है, उनसे पूर्ण विनिमय दरों का आवंटन और उनका विश्लेषण। परियोजना के ढांचे के भीतर, जोड़ी दरों से पूर्ण विनिमय दरों में परिवर्तित करने के लिए एक पद्धति प्राप्त की गई थी। इसके लिए, निरपेक्ष मुद्रा ABS को परिभाषित किया गया है। सभी उपलब्ध मुद्राएँ ABS के संदर्भ में व्यक्त की जाती हैं।
प्रौद्योगिकी का एक विस्तृत विवरण
"मुद्रा जोड़े से पूर्ण विनिमय दरों तक" लेख में दिया गया है।
समस्या के बारे में
यह लेख विनिमय दरों के सामंजस्य के गुणात्मक विश्लेषण की समस्या को संबोधित करता है।
मुद्राओं के बीच संबंधों का अध्ययन करने की आवश्यकता निवेश पोर्टफोलियो में वित्तीय साधनों के चयन की आवश्यकताओं और उनसे जुड़ी अन्य मुद्राओं के आंकड़ों के आधार पर मुद्राओं के व्यवहार की भविष्यवाणी करने की क्षमता के कारण है।
निवेश पोर्टफोलियो में उच्च बहुआयामी कनेक्टिविटी वाले उपकरणों को शामिल करना उचित है। यह पोर्टफोलियो के समग्र जोखिम को कम करता है।
और, यदि आपको उच्च स्तर की कनेक्टिविटी के साथ उपकरण मिलते हैं, तो कुछ के व्यवहार के आधार पर, आप दूसरों के व्यवहार का अनुमान लगा सकते हैं।
प्रयोग के बारे में
विधि चयन
प्रयोग के लिए प्रारंभिक डेटा के रूप में, पूर्ण विनिमय दरों के साथ डेटा श्रृंखला होती है (
स्रोत फ़ाइल देखें
। "पूर्ण विनिमय दरें" शीट )।

संख्यात्मक डेटा की एक श्रृंखला की कनेक्टिविटी का अध्ययन करने के लिए, पियर्सन सहसंबंध (देखें
सहसंबंध - विकिपीडिया ) का उपयोग करना सबसे अच्छा है।
सहसंबंध गुणांक में "-1" से "+1" तक मान है। बड़े नकारात्मक मूल्य एक मजबूत बहुआयामी संबंध का संकेत देते हैं। बड़े सकारात्मक मूल्य मजबूत यूनिडायरेक्शनल कनेक्टिविटी का संकेत देते हैं। "0" के गुणांक की निकटता संचार की अनुपस्थिति को इंगित करती है।

आप क्या पाना चाहते हैं?
प्रयोग का उद्देश्य उच्च स्तर की संयोजकता वाली मुद्राओं के समूहों को प्राप्त करना है। इसके अलावा, संचार का संकेत भी रुचि है।
स्थान
सभी गणना वुल्फराम मैथमेटिका प्रणाली (
वुल्फराम मैथमेटिका - विकिपीडिया ) देखें। और हम
वुल्फराम का उपयोग करेंगे। मुक्त बादल संसाधनों का उपयोग करें।
निर्दिष्ट संसाधन आपको गणना के साथ ऑनलाइन नोटबुक बनाने की अनुमति देता है और आपको सामान्य देखने के लिए पहुंच प्रदान करने की अनुमति देता है। इस प्रयोग की नोटबुक
यहाँ स्थित
है ।

योजना
हम निम्नलिखित योजना के अनुसार गणना करेंगे।
सबसे पहले, हम सहसंबंध मैट्रिक्स की गणना करते हैं। मैट्रिक्स के कॉलम और पंक्तियाँ व्यक्तिगत मुद्राओं के अनुरूप होंगी। स्तंभ और पंक्ति के चौराहे पर युग्म सहसंबंध गुणांक होगा।
अगला, हम सबसे मजबूत संबंधों के साथ मुद्राओं के जोड़े का चयन करते हैं।
ग्राफ़ पर चयनित जोड़े रखें (
ग्राफ़ (गणित) - विकिपीडिया ) देखें।
ग्राफ की नोड्स मुद्राएं हैं। ग्राफ के किनारों से मुद्राओं के बीच संबंध का संकेत मिलेगा। रिब का रंग बंधन संकेत का संकेत देगा। ग्रीन एक सकारात्मक संबंध को इंगित करता है, और लाल एक नकारात्मक संबंध को इंगित करता है।
गणनाओं के संकेतित अनुक्रम को पूर्ण पाठ्यक्रम और उनके परिवर्तनों के लिए दोनों किया जाएगा। निरपेक्ष पाठ्यक्रमों के संबंध का विश्लेषण आपको धीमी प्रक्रियाओं (एक दिन से अधिक) का पता लगाने की अनुमति देता है। पूर्ण विनिमय दरों में परिवर्तन के बीच संबंध का विश्लेषण हमें मुद्राओं (एक दिन) के बीच तेजी से कनेक्शन की जांच करने की अनुमति देगा।
परिणाम
सैंपलिंग की गहराई
स्रोत फ़ाइल में पिछले 150 दिनों का डेटा है। उनके अनुसार, गणना की जाएगी।
मुद्रा मेघ
प्रयोग में 45 मुद्राएं शामिल थीं।
 स्रोत फ़ाइल की "मुद्रा सारांश" शीट
स्रोत फ़ाइल की "मुद्रा सारांश" शीट पर मुद्राओं की एक पूरी सूची देखी जा सकती है।
पूर्ण दर सहसंबंध
ऊपर (देखें। योजना), यह पूर्ण दरों के लिए सहसंबंध मैट्रिक्स की गणना करने की योजना बनाई गई थी। परिणाम नीचे चित्र में दिखाया गया है।

यहां, लाल एक सकारात्मक संबंध से मेल खाता है, और नीला एक नकारात्मक से। समझने के लिए, एक ग्रेडेशन स्केल दिया जाता है। नीचे और बाईं ओर मुद्रा टिकर (संक्षिप्त नाम) हैं।
पूर्ण दर निर्भरता ग्राफ
सहसंबंध मैट्रिक्स ने मुद्राओं के दो समूहों को एक उच्च डिग्री कनेक्टिविटी के साथ अलग करना संभव बना दिया। ऐसा करने के लिए, 0.9 से अधिक सहसंबंध वाले जोड़े चुने गए और ग्राफ़ में स्थानांतरित कर दिए गए।

पहले समूह ने अमेरिकी डॉलर पर बहुत अधिक निर्भरता के साथ मुद्राओं को इकट्ठा किया। यहां तेल में कारोबार करने वाले चार अरब देशों, हांगकांग डॉलर और अमेरिकी डॉलर की मुद्राएं हैं। सभी निर्भरताएं सकारात्मक (यूनिडायरेक्शनल) हैं।
दूसरे समूह ने यूरोपीय मुद्राओं को इकट्ठा किया। केंद्र में खुद यूरो और इसके आसपास पोलैंड, रोमानिया और डेनमार्क की मुद्राएं हैं। सभी निर्भरताएं सकारात्मक (यूनिडायरेक्शनल) हैं।
संपूर्ण दरों में सापेक्ष परिवर्तन
आगे के शोध के लिए, हमने पूर्ण दरों में सापेक्ष परिवर्तनों की श्रृंखला की गणना की। गणना के लिए सूत्र निम्नानुसार है।

क्रमिक मूल्यों के बीच का अंतर दोनों के पहले से संबंधित होगा। इस प्रकार, हम पूर्ण दर में एक सापेक्ष परिवर्तन प्राप्त करेंगे।
पूर्ण दरों में सापेक्ष परिवर्तनों का सहसंबंध
निरपेक्ष पाठ्यक्रमों के लिए, हम निरपेक्ष पाठ्यक्रमों के सापेक्ष माप के लिए सहसंबंध मैट्रिक्स प्राप्त करते हैं। हम मैट्रिक्स का एक ग्राफिकल डिस्प्ले देते हैं।
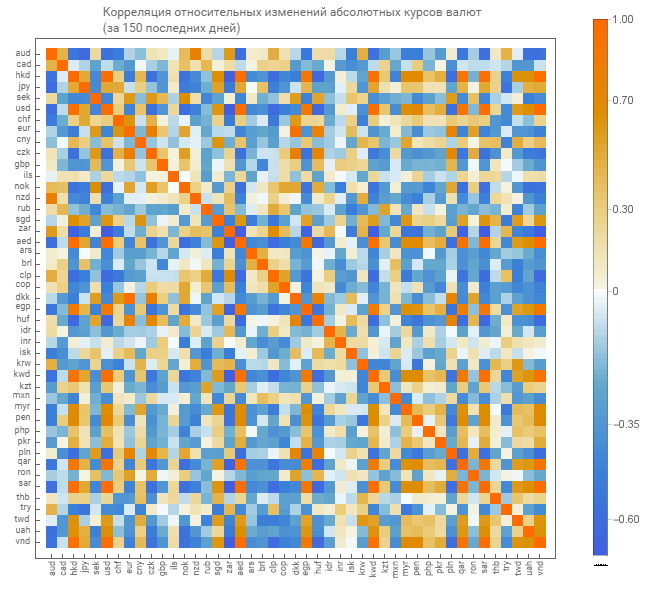
पहले से ही हल्का टन का एक मैट्रिक्स है। जो कि कुछ हद तक कनेक्टिविटी को इंगित करता है।
पूर्ण दरों में सापेक्ष परिवर्तन की निर्भरता ग्राफ
रिश्तेदार परिवर्तनों के सहसंबंध मैट्रिक्स से, हम उच्च स्तर की संयोजकता वाली मुद्राओं का चयन करते हैं। केवल नमूना स्तर यहां पहले से ही 0.6 है (यहां और ऊपर, इस गुणांक को ग्राफ़ के आउटपुट के लिए कम संख्या में जोड़े के विचार से चुना गया था)।

सापेक्ष परिवर्तनों के मामले में मुद्राओं के 3 समूह प्राप्त हुए। ऊपरी समूह ने ऑस्ट्रेलिया और न्यूजीलैंड की मुद्राओं को मिलाया। निचला समूह यूरोपीय मुद्राओं को इकट्ठा करता था। हांगकांग डॉलर के आसपास के मध्य समूह ने संयुक्त राज्य अमेरिका, वियतनाम, पांच अरब देशों - तेल निर्यातकों, दक्षिण अफ्रीका और पेरू की मुद्राओं को जोड़ा।
इसके अलावा, दक्षिण अफ्रीकी रैंड पर उच्च नकारात्मक निर्भरता में एक दिलचस्प विशेषता है।
निष्कर्ष
प्रयोग के परिणामस्वरूप, हम निम्नलिखित प्राप्त करने में सफल रहे।
सहसंबंध मैट्रिक्स डेटा को गणितीय ग्राफ में डालना सहसंबंध मैट्रिक्स के लिए एक अच्छा दृश्य अभ्यास है। इस पद्धति का आगे अनुप्रयोग संख्या श्रृंखला के समूह में संबंधों की समझ को सरल करेगा।
मुद्रा बाजारों के क्लस्टरिंग के लिए एक औपचारिक तरीका पाया जाता है। एशिया, ओशिनिया के साथ यूरोप, अमेरिका के बाजारों को औपचारिक रूप से अलग करना संभव था। यह विधि विभिन्न देशों के बाजारों के बीच पारस्परिक प्रभावों को प्रकट करने और वित्तीय विश्लेषक के लिए एक अच्छा साधन बनने के लिए मार्ग को काफी छोटा कर सकती है।
अमेरिकी डॉलर के साथ निवेश पोर्टफोलियो में दक्षिण अफ्रीकी रैंड को शामिल करने से इस तरह के पोर्टफोलियो के जोखिम कम हो जाएंगे।
लेखों की सूची