कजाकिस्तान की कंपनी के शेयर की कीमत के लिए VaR और CONVaR का अनुमान

पिछले दशकों में विश्व अर्थव्यवस्था नियमित रूप से वित्तीय संकट के इस भंवर में पड़ जाती है जिसने प्रत्येक देश को प्रभावित किया है। यह लगभग मौजूदा वित्तीय प्रणाली के पतन का कारण बना, इस तथ्य के कारण, गणितीय और आर्थिक मॉडलिंग के विशेषज्ञ सभी वित्तीय दुनिया में संपत्ति और पोर्टफोलियो के नुकसान को नियंत्रित करने के तरीकों का उपयोग करने के लिए बन गए हैं (लेचनर, एलए, और ओवर्ट, टीसी (२०१०)। बाजार के व्यवहार और इसकी स्थिरता (ibid) का आकलन करने के लिए एक आर्थिक प्रक्रिया के गणितीय मॉडलिंग की दिशा में एक बढ़ती प्रवृत्ति है। नियंत्रण और ठीक से खतरों का आकलन करने के लिए आवश्यक ध्यान दिए बिना, हर कोई समझता है कि यह ट्रिगर करने में सक्षम है। संगठन के विकास में भारी लागत या यहां तक ​​कि दिवालिया हो जाना।

मूल्य पर जोखिम (VaR) अंततः वित्त क्षेत्र और इसके नियामक (Engle, R., और Manganelli S., 2004) के संस्थानों के बीच जोखिम को पकड़ने के लिए एक नियमित दृष्टिकोण रहा है। मॉडल को मूल रूप से निवेश पोर्टफोलियो में नुकसान की मात्रा का अनुमान लगाने के लिए एक निश्चित अवधि के भीतर और साथ ही घटना होने की संभावना पर लगाया जाता है। वित्तीय क्षेत्र में वीएआर का उपयोग करने के तथ्य के अलावा, विभिन्न क्षेत्रों में जोखिम पर मूल्य के मूल्यांकन के बहुत सारे उदाहरण हैं जैसे कि स्वास्थ्य कर्मचारियों के प्रबंधन के लिए स्वास्थ्य प्रबंधन संसाधन झिनौरी, एन (2016) को विकसित करने की उम्मीद करना। वास्तविक प्रयोग में इसकी लागू प्रधानता के बावजूद, मॉडल में मूल्यांकन में कमियां हैं, (ibid)।

रिपोर्ट का लक्ष्य मौजूदा वीआर मॉडल का वर्णन है जिसमें इसके एक उन्नयन संस्करण, अर्थात्, सशर्त मूल्य पर जोखिम (सीवीआरआर) शामिल है। अगले भाग और खंड 3 में, मूल्यांकन एल्गोरिथ्म और मॉडल के परीक्षण के बारे में बताया गया है। एक ज्वलंत चित्रण के लिए, लंबे समय की अवधि में वित्तीय स्टॉक एक्सचेंज बाजार में कजाकिस्तान की एक कंपनी की संपत्ति पर अनुमानित नुकसान का अनुमान है। अंतिम खंड 4 और 5 शोध कार्य के निष्कर्षों पर चर्चा और प्रदर्शन करते हैं।

पृष्ठभूमि

ऐसा माना जाता है कि 40 साल पहले तक विशाल वित्तीय संगठनों द्वारा वीआरआर का पहला उपयोग और परिणाम में वीआर अन्य व्यापारिक फर्मों के बीच लोकप्रिय हो गया था, यहां तक ​​कि वित्तीय नियामकों ने मॉडल (लिंसमीयर, टीजे, और पियर्सन, एनडी पर ध्यान दिया था। 2000)। उदाहरण के लिए, अमेरिकी प्रतिभूति और विनिमय आयोग ने 1997 में (जोखिम) की बाजार जोखिम और संपत्ति की गणना के लिए मात्रात्मक तरीकों की सूची में वीएआर को अंकित किया।

दरअसल, लेचनर, एलए, और ओवर्ट, टीसी (2010) के साथ-साथ लिंसमीयर, टीजे और पियरसन, एनडी (2000) के लेखों के अनुसार, वीएआर मौद्रिक इकाइयों में व्यक्त एक अनुमानित समीकरण है जो परिमाण सीमा में नुकसान से अधिक नहीं है। एक निश्चित समयावधि के दौरान और आत्मविश्वास का स्तर। आमतौर पर, मॉडल आकलन का आत्मविश्वास स्तर (99%, 97.5%, 95%) या दूसरे शब्दों में संभावना है कि कुछ प्रतिकूल मामला हुआ होगा और बाजार पर प्रभाव 1, 2.5 और 5 प्रतिशत (ibid) के बराबर है।

VaR का प्रसिद्ध समीकरण वर्णित किया जा सकता है (फेल्प्स एस, 2018):

$$$(1) \ _ वीआर (एक्स) = \ मिनट \ \ {एक्स \ \ एप्सिलोन \ आर: १-एफ_एक्स (-एक्स) \ जिक \ अल्फा \}$

जहां एक्स एक यादृच्छिक चर है जो पोर्टफोलियो के मूल्य की राशि का प्रदर्शन करता है, और एक संचयी वितरण फ़ंक्शन (ibid) है।

दूसरी ओर, हूपर जीपी (1996, लेचनर, एलए, और ओवेर्ट, टीसी 2010 में उद्धृत) एक बहुत ही प्राथमिक तरीके से आत्मविश्वास अल्फा परिभाषित के साथ VaR को दर्शाता है:

$$$(2) \ VaR ^ \ अल्फा (एक्स) = \ सिग्मा \ sqrt {\ डेल्टा टी} एन ^ {- 1} \ अल्फा$

जहाँ $$$\ _ सिग्मा$ चयनित स्टॉक रिटर्न का मानक विचलन है, $$$\ डेल्टा टी$ निश्चित समयावधि का वर्गमूल है और $$$N ^ {- 1}$ सामान्य वितरण के लिए संचयी वितरण फ़ंक्शन (CDF) है (Lechner, LA, और Ovaert, TC 2010)।

यद्यपि वीआरआर एक अच्छी तरह से ज्ञात और नियंत्रित तरीका है, जो तय किए गए पोर्टफोलियो जोखिम का अनुमान लगाने के लिए है, एक मामले में कमियां हैं जब अंतिम बाजार के मुद्दों की भेद्यता को मापते हैं, अर्थात्, उदाहरण से संबंधित है चरम बाजार की घटनाओं की पूंछ में पर्याप्त रूप से नहीं पकड़ा गया है। सामान्य वितरण (Capi theski, MJ 2015)। इस समस्या को हल करने के लिए, सशर्त मूल्य जोखिम (CVaR) बनाया गया था जो कि VaR (ibid) के बजाय हानि के अपेक्षित मूल्य पर विचार करता है। CVaR के रूप में परिभाषित करता है:

$$$(3) \ CVaR ^ \ अल्फा (एक्स) = \ frac {1} {\ अल्फा} \ int ^ \ Alpha_0 VaR ^ \ बीटा (एक्स) डी \ बीटा = \ frac {-1} {\ अल्फा} q ^ \ बीटा (एक्स) डी \ बीटा$

$$$(4) \ CVaR ^ \ अल्फा (एक्स) = - \ frac {1} {\ अल्फा} (ई [एक्स 1 _ {\ _ x \ leq q ^ \ अल्फा (x) \}}] + q ^ \ अल्फा (एक्स) (\ अल्फा-पी [एक्स \ लीक क्यू ^ \ अल्फा (एक्स)])$

जहां अहं डी.-एच। et.al (1999, कैपिस्की, एमजे 2015 में उद्धृत) व्याख्या $$$-q ^ \ अल्फा (एक्स)$
संभावना के साथ एक्स यादृच्छिक चर (स्टॉक मूल्य की वापसी) के वीआर के रूप में $$$\ अल्फा$ और X की ऊपरी मात्रा के रूप में परिभाषित करता है।

इसके अलावा, Acerbi C. और Tasche D. (2002, Capi ,ski, MJ 2015 में उद्धृत) पुष्टि करते हैं, "CVAR एक सुसंगत जोखिम उपाय है"। रॉकफेलर, आरटी, और यूरेसेव, एस (2000) ने नोटिस किया कि सीवीआरआर में अतिरिक्त विशेषताएं हैं: संक्रमण-संतुलन, सकारात्मक सजातीय, उत्तल और आदि।

लेख का निम्नलिखित अध्याय जोखिम (VaR) और जोखिम पर सशर्त मूल्य (CVAR) में अच्छी तरह से ज्ञात मूल्य के कार्यान्वयन को प्रदर्शित करता है, जिसे रॉकफेलर, आरटी और यूरीव, एस (2000) के काम में अपेक्षित कमी (ईएस) के रूप में घोषित किया गया है। वास्तविक डेटा पर सूचना प्रौद्योगिकी का उपयोग करके।

क्रियाविधि

आइए वीएआर की गणना के लिए सबसे अधिक उपयोग किए जाने वाले तरीकों पर विचार करें, साथ ही साथ इसके फायदे और नुकसान।

Lechner, LA, और Ovaert, TC (2010) की रिपोर्ट के अनुसार, ऐतिहासिक सिमुलेशन VaR और इसके संशोधन का मूल्यांकन करने के लिए एक व्यापक दृष्टिकोण है। डेटा के ऐतिहासिक मॉडलिंग में, हम पोर्टफोलियो के लिए वित्तीय उतार-चढ़ाव के मूल्यों को लेते हैं जो पहले से ही पिछले मापों से ज्ञात हैं। इसलिए यह केवल तर्कसंगत अनुक्रम है कि इस पद्धति का नुकसान इसके बारे में जानकारी के एक टुकड़े के बिना पोर्टफोलियो के लिए भविष्यवाणियों के निर्माण की असंभवता है। मोंटे कार्लो विधि कई मायनों में ऐतिहासिक मॉडलिंग की पद्धति के समान है, जिसका उपयोग उच्च-सटीक तकनीक के लिए किया जाता है, मुख्य स्पष्ट अंतर यह है कि मोंटे कार्लो सिमुलेशन की गणना वास्तविक डेटा पर आधारित नहीं है, लेकिन यादृच्छिक रूप से उत्पन्न मूल्यों पर महसूस की जाती है। इस पद्धति का लाभ बड़ी संख्या में स्थितियों के रूप में विचार करने की संभावना है, और चरम स्थितियों में बाजार के व्यवहार का अनुकरण करने के साथ-साथ जोखिम वाले कारकों और एक पोर्टफोलियो में परिवर्तन के बीच कोई सन्निकटन की आवश्यकता नहीं है (ग्लासमैन, पी।, हीडलबर्गर, पी। । और शहाबुद्दीन, पी।, 2002)। स्पष्ट दोष इस दृष्टिकोण (ibid) को लागू करने के लिए आवश्यक बड़े कम्प्यूटेशनल संसाधन हैं।

स्वाभाविक रूप से, ये वीआर मॉडल की गणना के लिए केवल ये तरीके नहीं हैं। इसके अलावा, मूल्य निर्धारण के सरल रेखीय और द्विघात मॉडल दोनों हैं, और विविधताओं का एक जटिल तरीका है, जो निबंध में शामिल नहीं थे।

डेटा विश्लेषण

सटीक मूल्यांकन के परीक्षण के लिए माध्यमिक डेटा के रूप में, काजी मिनरल्स का स्टॉक लिया जाता है। काम को स्पष्ट करने के लिए, एक मॉडल में सिमुलेशन के लिए समायोजित बंद मूल्य लिया जाता है। काज़ मिनरल्स कंपनी (KAZ.L) के शेयर लंदन स्टॉक एक्सचेंज (LSE) पर कज़ाकिस्तान की फर्मों के साथ-साथ प्रीमियम इक्विटी कमर्शियल कंपनियों की सूची (लंदन स्टॉक एक्सचेंज, 2019) में वर्गीकृत किए गए हैं। यह इकाई खुद को कजाखस्तान में बड़े पैमाने पर तांबा खनन कंपनी के रूप में प्रस्तुत करती है (Kazmineral.com 2019)।

शेयर की कीमत का ऐतिहासिक डेटा याहू फाइनेंस वेब साइट (Finance.yahoo.com, 2019) से डाउनलोड किया गया है। कार्य की वैधता सुनिश्चित करने के लिए, 22 मार्च, 2018 से 22 मार्च, 2019 तक एक वर्ष की अवधि देखी जाती है। इसके अलावा, जानकारी में व्यवधान से बचने के लिए, विश्लेषण में, KAZ.L शेयर की कीमत का ऐतिहासिक डेटा कोमा-सेपरेटेड वैल्यूज़ (CSV) प्रारूप में डाउनलोड किया गया है, इस तथ्य के कारण कि CSV प्रारूप Microsoft Excel प्रोग्राम (Excel) द्वारा संगत है । चित्र 1 में एक्सेल का उपयोग करके परियोजना के चुने हुए डेटा को रेखा ग्राफ के रूप में प्रस्तुत किया गया है।

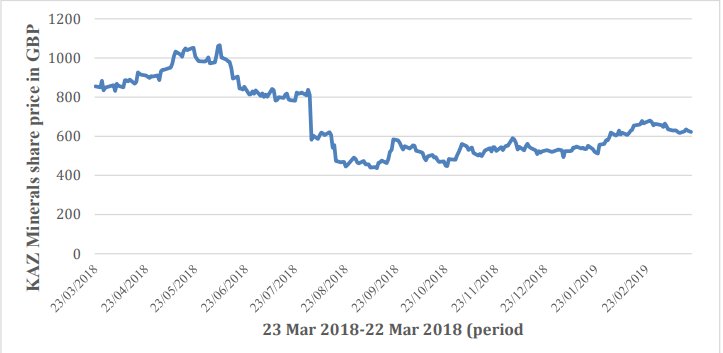
चित्र 1. एक वर्ष के लिए परिवर्तन काज़ मिनरल्स के स्टॉक मूल्य की गति

रिपोर्ट समयरेखा की सीमा के कारण, मूल्यांकन मॉडल के कार्यान्वयन के लिए पायथन जैसी प्रोग्रामिंग भाषा का उपयोग करने के बजाय, डेटा का पूरी तरह से एक्सेल में विश्लेषण किया जाता है।

निष्कर्ष

पिछले खंड में, वैर और सीवीआरआर समीकरण के आधार पर एक पोर्टफोलियो में संभावित नुकसान का पूर्वानुमान लगाने के लिए और 23 मार्च, 2018 से 23 मार्च, 2019 तक काज मिनरल्स के शेयर मूल्य में बदलाव का इस्तेमाल किया गया था, आधिकारिक वेब स्रोत याहू फाइनेंस (फाइनेंस। याहू) से डाउनलोड किया गया था। com, 2019)। चुने गए अवधि से दोनों समीकरण प्रत्येक तिथि के लिए निष्पादित किए गए।

तालिका 1 मतलब व्यापार दैनिक रिटर्न, रिटर्न का एक मानक विचलन, रिटर्न का एक न्यूनतम मूल्य और इस उदाहरण के लिए रिटर्न का अधिकतम मूल्य दर्शाता है।

तालिका 1. शेयर का मतलब रिटर्न और रिटर्न का मानक विचलन है

इसी का मतलब -0.0006 है और चयनित विशिष्ट सुरक्षा काज़ मिनरल्स के लिए रिटर्न का मानक विचलन 0.0355 है। क्या अधिक है कि रिटर्न का विचरण 0.0013 है। इसके अतिरिक्त, यह निश्चित रूप से रेखांकित किया जाना चाहिए कि वी, डीएनसी, और गोनपॉट, पी। एन (2014) के अनुसंधान कार्य में कजाकिस्तान के स्टॉक रिटर्न ने अस्थिरता में महत्वपूर्ण मूल्य दिखाया है, लेकिन अनुमान पूर्व में कजाकिस्तान स्टॉक एक्सचेंज के सूचकांक से संबंधित था। 2008 के बाद की अवधि। इसके अलावा, यह उल्लेख किया जाना चाहिए कि रिटर्न के बीच अधिकतम मूल्य 0.0998 है, साथ ही रिटर्न के बीच न्यूनतम मूल्य हानि वितरण में -0.2829 है। तालिका 2 23 मार्च, 2018 से 22 मार्च, 2019 तक लंदन स्टॉक एक्सचेंज में पाउंड स्टर्लिंग (GBP) में समायोजित स्टॉक मूल्य (KAZ.L) के बीच अधिकतम और न्यूनतम मूल्य प्रस्तुत करता है।

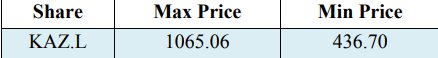
तालिका 2. GBP में अधिकतम और न्यूनतम काज खनिज स्टॉक मूल्य

निम्न चरण आत्मविश्वास स्तर के लिए जोखिम (VaR) और जोखिम के सशर्त मूल्य (CVAR) पर मूल्यांकन मूल्य है - 0.99, 0.972 और 0.95। तालिका 3 में मानों का पता चलता है।

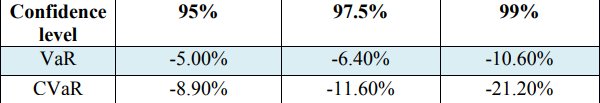
तालिका 3. रिटर्न के VaR और CVaR मान

सिमुलेशन का नमूना आकार एक वर्ष के दौरान 23 मार्च, 2018 से 22 मार्च, 2019 तक 252 यूनिट लिया गया है।

विचार-विमर्श

रिपोर्ट में, वीएआर और सीवीआरआर समीकरण अल्पकालिक अवधि में कजाकिस्तान की कंपनी के शेयर की कीमत के अनुमान मॉडल के मामले में विश्वसनीय मूल्य प्रदर्शित करते हैं। एक तरफ इन मूल्यों के साथ, दोनों तरीके निवेश पोर्टफोलियो (लिंसमेयर, टीजे, और पीयरसन, एनडी 2000; लेचनर, ला, और ओवर्ट, टीसी 2010) के लिए खतरों के मूल्य का आकलन करने के लिए पर्याप्त परिणाम प्रस्तुत करते हैं।

इसके अलावा, तालिका 2 के निष्कर्षों के अनुसार, अगला नोटिस सीधा है कि CVRR के लिए मान सभी विश्वास स्तर के उपायों द्वारा VaR मूल्यों की तुलना में अधिक बड़े पैमाने पर हैं। यह इस तथ्य से स्पष्टीकरण दिया जा सकता है कि सीवीआरआर ने पोर्टफोलियो के औसत जोखिम को चुना है जिसके परिणामस्वरूप यह वीएआर की तुलना में नुकसान वितरण की पूंछ पर अधिक संवेदनशील है। यह एक बार फिर साबित होता है कि सीवीआरआर एक सुसंगत जोखिम है (एसरबी सी और टेश डी।, 2002, कैपिस्की, एमजे 2015, रॉकफेलर, आरटी, और यूरेसेव, एस 2000 में उद्धृत)। उदाहरण के लिए, दोनों अनुमान मॉडल की पर्याप्तता के संबंध में, आत्मविश्वास के स्तर के साथ 99% VaR और CVaR स्टॉक के रिटर्न से महत्वपूर्ण प्रतिशत नुकसान का वर्णन करते हैं। सटीक होने के लिए, यह पता लगाया जा सकता है कि VaR -10.60% है और CVaR -21.20% है। यह स्पष्ट है कि सीवीएआर के बड़े पैमाने पर माप के कारण किसी दिए गए आत्मविश्वास के स्तर के साथ 99% है क्योंकि इस अवधि के दौरान स्टॉक मूल्य की सीमा, अधिकतम कीमत क्रमशः 1065.06 GBP न्यूनतम स्टॉक मूल्य 436.70 GBP है।

निष्कर्ष

उपरोक्त सब कुछ पर विचार करने के बाद, यह स्पष्ट रूप से फिर से उल्लेख किया जाना चाहिए कि रिपोर्ट का उद्देश्य 23 मार्च, 2018 से 22 मार्च, 2019 की अवधि में कजाकिस्तान की कंपनी (काजी मिनरल्स) के लिए संभावित नुकसान के मूल्य का आकलन प्रदर्शित करना है। वैल्यू एट रिस्क (VaR) और कंडिशनल वैल्यू एट रिस्क (CVaR) समीकरणों पर गठित। सिमुलेशन से प्रदर्शन एक ही समय अवधि में एक दूसरे की तुलना में हैं। परिणाम प्रत्येक विधि के लिए महत्वपूर्ण मूल्य दिखाते हैं और उसी क्षेत्र पर पिछले काम को साबित करते हैं कि सीवीएआर में वाएआर (एसरबी सी और टेश डी।, 2002 की तुलना में अधिक सटीक उपाय हैं, कैपिस्की, एमजे 2015 में उद्धृत; रॉकफेलर, आरटी; और यूरेसेव, S.2000)।

आलोचना के बावजूद, वीआर दिन को पेश करने के लिए सभी वित्तीय संस्थानों में एक व्यापक उपकरण है और इसके संशोधन संस्करण की एक विस्तृत श्रृंखला है। गहन शोध में जटिल गणना की बाधाओं के कारण, प्रयोग माइक्रोसॉफ्ट एक्सेल का उपयोग करके किया जाता है, जैसे कि पायथन जैसी प्रोग्रामिंग भाषा का उपयोग किया जाता है, साथ ही रिपोर्ट में परिणाम सामने आते हैं। निबंध के परिणाम स्टॉक एक्सचेंज उद्योग, बीमा उद्योग और निवेश उद्योग में पोर्टफोलियो के लिए जोखिम के जटिल मूल्यांकन उपाय का उपयोग करके आगे के काम के लिए एक तहखाने के रूप में सक्षम हैं।