ब्लैक होल के ऊष्मप्रवैगिकी

हैप्पी कॉस्मोनॉटिक्स डे! हमने प्रिंटिंग हाउस को "ब्लैक होल के बारे में एक छोटी किताब" सौंपी। यह इन दिनों था कि खगोलविदों ने पूरी दुनिया को दिखाया कि ब्लैक होल कैसे दिखते हैं। संयोग? हम ऐसा नहीं सोचते;) तो इंतजार करें, जल्द ही एक अद्भुत पुस्तक दिखाई देगी, जिसे स्टीफन गैबर और फ्रैंस प्रिटोरियस द्वारा लिखा गया है, जिसका अनुवाद अद्भुत पुलकोवो खगोल विज्ञानी उर्फ ​​एस्ट्रोल्ड किरिल मस्लेंनिकोव द्वारा किया गया है, पौराणिक व्लादिमीर ऑर्डिन ने वैज्ञानिक संपादन किया और ट्रैजोरी फाउंडेशन ने इसके प्रकाशन का समर्थन किया।

कट के नीचे "ब्लैक होल के ऊष्मप्रवैगिकी"।

अब तक, हमने ब्लैक होल को खगोलीय पिंडों के रूप में माना है जो सुपरनोवा विस्फोटों के दौरान या आकाशगंगाओं के केंद्र में स्थित हैं। हम उन्हें परोक्ष रूप से देखते हैं, उनके करीब सितारों की तेजी को मापते हैं। 14 सितंबर, 2015 को LIGO रिसीवर द्वारा गुरुत्वाकर्षण तरंगों का प्रसिद्ध पंजीकरण काले रंग के टकराव की अधिक प्रत्यक्ष टिप्पणियों का एक उदाहरण बन गया। गणितीय उपकरण जो हम ब्लैक होल की प्रकृति की बेहतर समझ हासिल करने के लिए उपयोग करते हैं, वे हैं: अंतर ज्यामिति, आइंस्टीन समीकरण और शक्तिशाली विश्लेषणात्मक और संख्यात्मक तरीके जो आइंस्टीन के समीकरणों को हल करने के लिए और अंतरिक्ष समय ज्यामिति का वर्णन करने के लिए उपयोग किए जाते हैं: ब्लैक होल उत्पन्न करते हैं। और जैसे ही हम ब्लैक होल द्वारा उत्पन्न अंतरिक्ष-समय का एक पूर्ण मात्रात्मक विवरण दे सकते हैं, ज्योतिषीय दृष्टिकोण से ब्लैक होल के विषय को बंद माना जा सकता है। व्यापक सैद्धांतिक परिप्रेक्ष्य में, अनुसंधान के लिए अभी भी कई अवसर हैं। इस अध्याय का उद्देश्य आधुनिक ब्लैक होल भौतिकी की कुछ सैद्धांतिक उपलब्धियों के बारे में बात करना है, जिसमें थर्मोडायनामिक्स और क्वांटम सिद्धांत के विचारों को सापेक्षता के सामान्य सिद्धांत के साथ जोड़ा गया है, जिससे अप्रत्याशित नई अवधारणाओं को जन्म दिया गया है। मूल विचार यह है कि ब्लैक होल सिर्फ ज्यामितीय वस्तु नहीं हैं। उनके पास एक तापमान है, उनके पास भारी एंट्रोपी है और क्वांटम उलझाव की अभिव्यक्तियों को प्रदर्शित कर सकते हैं। ब्लैक होल भौतिकी के थर्मोडायनामिक और क्वांटम पहलुओं की हमारी चर्चा पिछले अध्यायों में प्रस्तुत ब्लैक होल में विशुद्ध रूप से ज्यामितीय अंतरिक्ष समय की विशेषताओं के विश्लेषण से अधिक स्केच और सतही होगी। लेकिन ये, और विशेष रूप से क्वांटम, पहलू ब्लैक होल के चल रहे सैद्धांतिक अध्ययन का एक आवश्यक और महत्वपूर्ण हिस्सा हैं, और हम यह बताने की बहुत कोशिश करेंगे, यदि जटिल विवरण नहीं है, तो कम से कम इन कार्यों की भावना।

सापेक्षता के शास्त्रीय सामान्य सिद्धांत में - अगर हम आइंस्टीन के समीकरणों के समाधान के अंतर ज्यामिति के बारे में बात करते हैं - ब्लैक होल वास्तव में इस अर्थ में काले हैं कि उनमें से कुछ भी नहीं निकल सकता है। स्टीफन हॉकिंग ने दिखाया कि जब हम क्वांटम प्रभावों को ध्यान में रखते हैं तो यह स्थिति पूरी तरह से बदल जाती है: ब्लैक होल एक निश्चित तापमान के विकिरण का उत्सर्जन करते हैं, जिसे हॉकिंग तापमान कहा जाता है। खगोलीय आकार के ब्लैक होल के लिए (यानी, तारकीय द्रव्यमान के ब्लैक होल से लेकर सुपरमासिव तक), कॉस्मिक माइक्रोवेव बैकग्राउंड के तापमान की तुलना में हॉकिंग तापमान नगण्य है - पूरे ब्रह्मांड को भरने वाले विकिरण, जो कि, खुद को हॉकिंग विकिरण का एक प्रकार माना जा सकता है। ब्लैक होल के तापमान को निर्धारित करने के लिए हॉकिंग द्वारा की गई गणनाएं ब्लैक होल के ऊष्मप्रवैगिकी नामक क्षेत्र में व्यापक शोध कार्यक्रम का हिस्सा हैं। इस कार्यक्रम का एक अन्य प्रमुख हिस्सा ब्लैक होल के एन्ट्रापी का अध्ययन है, जो एक ब्लैक होल के अंदर खोई गई सूचना की मात्रा को दर्शाता है। साधारण वस्तुएं (जैसे कि पानी का एक मग, शुद्ध मैग्नीशियम या एक तारा का एक बार) भी एन्ट्रापी है, और ब्लैक होल के ऊष्मप्रवैगिकी के केंद्रीय कथनों में से एक यह है कि इस आकार के एक ब्लैक होल में किसी भी अन्य पदार्थ के अधिक एन्ट्रापी होते हैं जिन्हें समायोजित किया जा सकता है। एक ही आकार का एक क्षेत्र, लेकिन एक ब्लैक होल के गठन के बिना।

लेकिन इससे पहले कि हम हॉकिंग विकिरण और ब्लैक होल के एन्ट्रापी से जुड़ी समस्याओं की चर्चा में गहराई से डूबते हैं, चलो क्वांटम यांत्रिकी, ऊष्मप्रवैगिकी, और उलझाव के क्षेत्रों में एक त्वरित भ्रमण करें। क्वांटम यांत्रिकी को मुख्य रूप से 1920 के दशक में विकसित किया गया था, और इसका मुख्य उद्देश्य पदार्थ के बहुत छोटे कणों, जैसे परमाणुओं का वर्णन करना था। क्वांटम यांत्रिकी के विकास ने भौतिकी के ऐसे मूल अवधारणाओं को एक व्यक्तिगत कण की सटीक स्थिति के रूप में नष्ट कर दिया: यह निकला, उदाहरण के लिए, कि जब एक परमाणु नाभिक के चारों ओर घूमता है तो इलेक्ट्रॉन की स्थिति ठीक से निर्धारित नहीं की जा सकती है। इसके बजाय, तथाकथित कक्षाओं को इलेक्ट्रॉनों को सौंपा गया था, जिसमें उनकी वास्तविक स्थिति केवल एक संभाव्य अर्थ में निर्धारित की जा सकती है। हमारे उद्देश्यों के लिए, हालांकि, यह महत्वपूर्ण है कि इस मामले की संभावना के साथ-साथ इस मामले को भी जल्दी से आगे बढ़ाया जाए। सबसे सरल उदाहरण लें: एक हाइड्रोजन परमाणु। यह एक निश्चित क्वांटम अवस्था में हो सकता है। हाइड्रोजन परमाणु की सबसे सरल अवस्था, जिसे ग्राउंड स्टेट कहा जाता है, सबसे कम ऊर्जा वाला राज्य है, और यह ऊर्जा ठीक-ठीक ज्ञात है। अधिक सामान्य अर्थ में, क्वांटम यांत्रिकी हमें (सिद्धांत रूप में) किसी भी क्वांटम प्रणाली की स्थिति को पूरी तरह से जानने की अनुमति देता है।

जब हम क्वांटम-मैकेनिकल सिस्टम के बारे में एक निश्चित प्रकार के प्रश्न पूछते हैं, तो संभावनाएँ सामने आती हैं। उदाहरण के लिए, यदि यह निश्चित रूप से ज्ञात है कि हाइड्रोजन परमाणु जमीन की स्थिति में है, तो हम पूछ सकते हैं: "इलेक्ट्रॉन कहाँ है?" और क्वांटम के नियमों के अनुसार
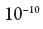
यांत्रिकी हम इस सवाल का केवल एक निश्चित संभावना का अनुमान लगाते हैं, लगभग कुछ इस तरह है: "इलेक्ट्रॉन शायद हाइड्रोजन परमाणु के नाभिक से आधे कोण तक की दूरी पर स्थित है" मीटर)। लेकिन हमारे पास एक निश्चित भौतिक प्रक्रिया के माध्यम से, इलेक्ट्रॉन की स्थिति को एक एंगस्ट्रॉम की तुलना में अधिक सटीक रूप से खोजने का अवसर है। यह प्रक्रिया, जो भौतिकी में काफी सामान्य है, एक इलेक्ट्रॉन में एक बहुत ही कम तरंग दैर्ध्य के साथ एक फोटॉन को लॉन्च करने में शामिल है (या, जैसा कि भौतिक विज्ञानी कहते हैं, एक इलेक्ट्रॉन पर एक फोटॉन को बिखरना) - उसके बाद हम इलेक्ट्रॉन के स्थान को एक सटीकता के साथ बिखरने के क्षण में पुनर्निर्माण कर सकते हैं, जो तरंग दैर्ध्य के लगभग बराबर है। फोटोन। लेकिन यह प्रक्रिया इलेक्ट्रॉन की स्थिति को बदल देगी, ताकि उसके बाद यह अब हाइड्रोजन परमाणु की जमीनी स्थिति में नहीं होगी और इसमें एक सटीक परिभाषित ऊर्जा नहीं होगी। लेकिन कुछ समय के लिए इसकी स्थिति लगभग बिल्कुल निर्धारित होगी (इसके लिए उपयोग किए जाने वाले फोटॉन की तरंग दैर्ध्य तक)। इलेक्ट्रॉन की स्थिति का प्रारंभिक मूल्यांकन केवल एक संभाव्य अर्थ में लगभग एक एंगस्ट्रॉम की सटीकता के साथ किया जा सकता है, लेकिन जैसे ही हमने इसे मापा, हम ठीक से जानते हैं कि यह किसके बराबर था। संक्षेप में, अगर हम किसी तरह से एक क्वांटम-मैकेनिकल प्रणाली को मापते हैं, तो, कम से कम आम तौर पर स्वीकृत अर्थों में, हम "जबरन" इसे एक निश्चित मूल्य के साथ एक राज्य देते हैं जिसे हम माप रहे हैं।

क्वांटम यांत्रिकी न केवल छोटे लोगों के लिए लागू है, लेकिन (जैसा कि हम मानते हैं) सभी प्रणालियों के लिए, लेकिन बड़ी प्रणालियों के लिए, क्वांटम-यांत्रिक नियम जल्दी से बहुत जटिल हो जाते हैं। प्रमुख अवधारणा क्वांटम उलझाव है, जिसका एक सरल उदाहरण स्पिन (रोटेशन) की अवधारणा है। व्यक्तिगत इलेक्ट्रॉनों में एक स्पिन होती है, इसलिए व्यवहार में एकल इलेक्ट्रॉन में स्पिन या चयनित स्थानिक अक्ष के संबंध में निर्देशित या नीचे हो सकता है। इलेक्ट्रॉन स्पिन एक मनाया मात्रा है, क्योंकि इलेक्ट्रॉन एक चुंबकीय पट्टी के क्षेत्र के समान एक कमजोर चुंबकीय क्षेत्र उत्पन्न करता है। फिर ऊपर की ओर इशारा करते हुए एक स्पिन का मतलब है कि इलेक्ट्रॉन का उत्तरी ध्रुव नीचे की ओर इशारा कर रहा है, और नीचे की ओर इशारा करते हुए एक स्पिन का मतलब है कि उत्तरी ध्रुव "ऊपर दिख रहा है"। दो इलेक्ट्रॉनों को एक संयुग्मित क्वांटम अवस्था में रखा जा सकता है, जिसमें उनमें से एक में एक स्पिन ऊपर की ओर निर्देशित होता है और दूसरा नीचे की ओर, लेकिन यह कहना असंभव है कि किस इलेक्ट्रॉन में कौन सा स्पिन है। संक्षेप में, एक हीलियम परमाणु की जमीनी अवस्था में, दो इलेक्ट्रॉन बिल्कुल ऐसी अवस्था में होते हैं, जिन्हें स्पिन-सिंगललेट कहा जाता है, क्योंकि दोनों इलेक्ट्रॉनों की कुल स्पिन शून्य के बराबर होती है। अगर हम इन दो इलेक्ट्रॉनों को उनके मोर्चे को बदलने के बिना अलग करते हैं, तो हम यह दावा करना जारी रख सकते हैं कि वे एक साथ स्पिन-सिंगललेट हैं, लेकिन हम अभी भी यह नहीं कह सकते हैं कि उनमें से प्रत्येक का स्पिन व्यक्तिगत रूप से क्या होगा। अब, यदि हम उनके एक स्पिन को मापते हैं और यह स्थापित करते हैं कि इसे निर्देशित किया गया है, तो हम पूरी तरह से सुनिश्चित होंगे कि दूसरा नीचे निर्देशित है। इस स्थिति में, हम कहते हैं कि पीठ उलझी हुई है - अपने आप में कोई एक निश्चित अर्थ नहीं है, जबकि एक साथ वे एक निश्चित मात्रा में हैं।

आइंस्टीन उलझने की घटना के बारे में बहुत चिंतित थे: यह सापेक्षता के सिद्धांत के बुनियादी सिद्धांतों को खतरा था। आइए स्पिन-सिंगलेट अवस्था में दो इलेक्ट्रॉनों के मामले पर विचार करें, जब वे अंतरिक्ष में एक दूसरे से बहुत दूर हैं। निश्चितता के लिए, उनमें से एक को ऐलिस और दूसरे बॉब को लेने दें। मान लीजिए कि ऐलिस ने अपने इलेक्ट्रॉन के स्पिन को मापा और पाया कि यह ऊपर की ओर था, और बॉब ने कुछ भी नहीं मापा। जब तक एलिस ने अपना माप पूरा नहीं किया, तब तक यह बताना असंभव था कि उनके इलेक्ट्रॉन का स्पिन क्या था। लेकिन जैसे ही उसने अपना माप पूरा किया, उसे पूरी तरह से पता चल गया था कि बॉब के इलेक्ट्रॉन का स्पिन नीचे की ओर निर्देशित है (अपने स्वयं के इलेक्ट्रॉन के स्पिन के विपरीत दिशा में)। क्या इसका मतलब यह है कि उसके माप ने तुरन्त बॉब के इलेक्ट्रॉन को राज्य में स्थानांतरित कर दिया जब उसका स्पिन नीचे की ओर निर्देशित होता है? यदि इलेक्ट्रॉनों को स्थानिक रूप से अलग किया जाता है तो यह कैसे हो सकता है? आइंस्टीन और उनके सहकर्मी नाथन रोसेन और बोरिस पोडॉल्स्की ने महसूस किया कि उलझी हुई प्रणालियों को मापने की कहानी इतनी गंभीर थी कि इसने क्वांटम यांत्रिकी के अस्तित्व को खतरे में डाल दिया। आइंस्टीन - पोडॉल्स्की - रोसेन (ईपीआर) द्वारा तैयार किए गए विरोधाभास का एक विचार प्रयोग करता है जो हमने अभी निष्कर्ष निकाला है: क्वांटम यांत्रिकी वास्तविकता का पूर्ण विवरण नहीं हो सकता है। अब, इसके बाद के सैद्धांतिक अनुसंधान और कई मापों के आधार पर, एक आम राय स्थापित की गई है कि ईपीआर विरोधाभास में त्रुटि है, और क्वांटम सिद्धांत सही है। क्वांटम-मैकेनिकल उलझाव असली है: उलझी हुई प्रणालियों का मापन सहसंबद्ध होगा, भले ही ये सिस्टम अंतरिक्ष-समय में बहुत दूर हो।

आइए हम उस स्थिति पर लौटते हैं जहां हमने एक स्पिन-एकल अवस्था में दो इलेक्ट्रॉनों को रखा और उन्हें ऐलिस और बॉब को वितरित किया। माप लेने से पहले हम इलेक्ट्रॉनों के बारे में क्या कह सकते हैं? कि दोनों एक साथ एक निश्चित क्वांटम अवस्था (स्पिन-सिंगलेट) में हैं। एलिसिन इलेक्ट्रॉन के स्पिन को समान रूप से ऊपर या नीचे निर्देशित किए जाने की संभावना है। अधिक सटीक रूप से, समान संभावना वाले इसके इलेक्ट्रॉन की क्वांटम स्थिति एक (स्पिन अप) या अन्य (स्पिन डाउन) हो सकती है। अब हमारे लिए प्रायिकता की अवधारणा पहले की तुलना में अधिक गहरा अर्थ लेती है। पहले, हमने एक निश्चित क्वांटम राज्य (हाइड्रोजन परमाणु की जमीनी स्थिति) पर विचार किया और देखा कि कुछ "असहज" प्रश्न हैं, जैसे कि, "इलेक्ट्रॉन कहाँ स्थित है?", ऐसे प्रश्न जिनके उत्तर केवल एक संभाव्य अर्थ में मौजूद हैं। यदि हमने "अच्छे" प्रश्न पूछे हैं, उदाहरण के लिए: "इस इलेक्ट्रॉन की ऊर्जा क्या है?", तो हमें उनके कुछ उत्तर मिलेंगे। अब ऐसे "अच्छे" प्रश्न नहीं हैं, जो हम ऐलिस के इलेक्ट्रॉन के बारे में पूछ सकते हैं, जिनके उत्तर बॉब के इलेक्ट्रॉन पर निर्भर नहीं करेंगे। (हम बेवकूफ सवालों के बारे में बात नहीं कर रहे हैं जैसे "क्या एलिसन के इलेक्ट्रॉन में एक स्पिन है?" - जिन सवालों के केवल एक ही उत्तर है।) इस प्रकार, हमें आधे-भ्रमित सिस्टमों में से एक के मापदंडों को निर्धारित करने के लिए संभाव्य भाषा का उपयोग करना होगा। निश्चित रूप से केवल तभी उत्पन्न होता है जब हम उन सवालों के बीच संबंध पर विचार करते हैं जो ऐलिस और बॉब अपने इलेक्ट्रॉनों के बारे में पूछ सकते हैं।

हमने जानबूझकर सबसे सरल क्वांटम-मैकेनिकल सिस्टम में से एक के साथ शुरू किया था जो कि हम जानते हैं: व्यक्तिगत इलेक्ट्रॉनों के स्पिन सिस्टम। यह आशा की जाती है कि क्वांटम कंप्यूटर ऐसे सरल प्रणालियों के आधार पर बनाए जाएंगे। व्यक्तिगत इलेक्ट्रॉनों या अन्य समतुल्य क्वांटम प्रणालियों की स्पिन प्रणाली को अब क्वबिट्स ("क्वांटम बिट्स" के लिए संक्षिप्त) कहा जाता है, जो डिजिटल कंप्यूटरों में सामान्य बिट्स द्वारा निभाई गई भूमिका के समान, क्वांटम कंप्यूटरों में उनकी भूमिका पर जोर देती है।

अब कल्पना कीजिए कि हमने प्रत्येक इलेक्ट्रॉन को बहुत अधिक जटिल क्वांटम प्रणाली के साथ बदल दिया है, न कि केवल दो क्वांटम अवस्थाओं के साथ। उदाहरण के लिए, उन्होंने एलिस और बॉब को शुद्ध मैग्नीशियम के बार दिए। इससे पहले कि एलिस और बॉब अलग-अलग दिशाओं में अपने अलग-अलग तरीके से जाएं, उनके बार बातचीत कर सकते हैं, और हम इस बात से सहमत होंगे कि ऐसा करने पर वे एक निश्चित सामान्य मात्रा में राज्य का अधिग्रहण करते हैं। जैसे ही ऐलिस और बॉब डायवर्ज करते हैं, उनके मैग्नीशियम बार बातचीत करना बंद कर देते हैं। जैसा कि इलेक्ट्रॉनों के मामले में, प्रत्येक पट्टी अनिश्चितकालीन अवस्था में होती है, हालांकि एक साथ, जैसा कि हम मानते हैं, वे पूरी तरह से निश्चित राज्य बनाते हैं। (इस चर्चा में, हम मानते हैं कि एलिस और बॉब अपनी आंतरिक स्थिति को विचलित किए बिना अपनी मैग्नीशियम सलाखों को स्थानांतरित करने में सक्षम हैं, जैसे कि हमने पहले यह मान लिया था कि ऐलिस और बॉब अपने मोच को बदलने के बिना अपने उलझे हुए इलेक्ट्रॉनों को अलग कर सकते हैं।) लेकिन अंतर। इस विचार प्रयोग और इलेक्ट्रॉनों के साथ प्रयोग के बीच यह है कि प्रत्येक पट्टी की क्वांटम स्थिति में अनिश्चितता भारी है। एक बार ब्रह्मांड में परमाणुओं की संख्या की तुलना में अधिक मात्रा में राज्यों को अच्छी तरह से अधिग्रहित कर सकता है। यह वह जगह है जहाँ ऊष्मप्रवैगिकी मंच में प्रवेश करती है। हालांकि, बहुत गलत तरीके से परिभाषित सिस्टम में कुछ अच्छी तरह से परिभाषित मैक्रोस्कोपिक विशेषताएं हो सकती हैं। इस तरह की एक विशेषता है, उदाहरण के लिए, तापमान। तापमान प्रायिकता का एक उपाय है जिसके साथ सिस्टम के किसी भी हिस्से में एक निश्चित औसत ऊर्जा होती है, जिसमें अधिक ऊर्जा होने की उच्च संभावना के अनुरूप उच्च तापमान होता है। एक अन्य थर्मोडायनामिक पैरामीटर एन्ट्रापी है, जो अनिवार्य रूप से उन राज्यों की संख्या के लघुगणक के बराबर है जो सिस्टम ले सकता है। मैग्नीशियम की एक पट्टी के लिए महत्वपूर्ण एक और थर्मोडायनामिक विशेषता इसका कुल चुंबकत्व है, अर्थात्, संक्षेप में, एक पैरामीटर जो दिखाता है कि स्पिन के साथ ऊपर की ओर इशारा करते हुए स्पिन के साथ बार में कितना अधिक इलेक्ट्रॉन हो सकते हैं।

हमने अपनी कहानी में थर्मोडायनामिक्स को उन प्रणालियों का वर्णन करने के तरीके के रूप में शामिल किया है जिनकी क्वांटम स्थिति अन्य प्रणालियों के साथ उलझने के कारण वास्तव में ज्ञात नहीं है। ऐसी प्रणालियों के विश्लेषण के लिए थर्मोडायनामिक्स एक शक्तिशाली उपकरण है, लेकिन इसके निर्माता इस तरह के आवेदन की उम्मीद नहीं करते थे। सादी कारनोट, जेम्स जूल, रूडोल्फ क्लॉउसियस XIX सदी की औद्योगिक क्रांति के अगुआ थे, और सभी सवालों के अपने सबसे व्यावहारिक में रुचि रखते थे: इंजन कैसे काम करते हैं? दबाव, आयतन, तापमान और ऊष्मा इंजनों का मांस और रक्त है। कार्नोट ने पाया कि ऊष्मा के रूप में ऊर्जा को कभी भी पूरी तरह से उपयोगी कार्यों में नहीं बदला जा सकता है जैसे कि सामान उठाना। ऊर्जा का हिस्सा हमेशा बर्बाद हो जाएगा। क्लॉसियस ने गर्मी से जुड़ी किसी भी प्रक्रिया के दौरान ऊर्जा हानि के निर्धारण के लिए एक सार्वभौमिक उपकरण के रूप में एन्ट्रापी के विचार के निर्माण में मुख्य योगदान दिया। उनकी मुख्य उपलब्धि यह अहसास था कि एन्ट्रापी कभी नहीं घटती - लगभग सभी प्रक्रियाओं में यह बढ़ता है। जिन प्रक्रियाओं में एन्ट्रापी बढ़ जाती है, उन्हें अपरिवर्तनीय कहा जाता है - ठीक है क्योंकि वे एन्ट्रापी को कम किए बिना रिवर्स नहीं कर सकते हैं। सांख्यिकीय यांत्रिकी के विकास में अगला कदम क्लॉउसियस, मैक्सवेल और लुडविग बोल्ट्ज़मैन (कई अन्य लोगों के बीच) द्वारा बनाया गया था - उन्होंने दिखाया कि एन्ट्रापी विकार का एक उपाय है। आमतौर पर जितना अधिक आप किसी चीज पर कार्य करते हैं, उतना ही आप वहां गड़बड़ करते हैं। और यहां तक ​​कि अगर आपने एक ऐसी प्रक्रिया विकसित की है जिसका लक्ष्य आदेश को बहाल करना है, तो इसके पाठ्यक्रम में अनिवार्य रूप से अधिक विनाशकारी रूप से इसे नष्ट कर दिया जाएगा, उदाहरण के लिए, जब गर्मी जारी होती है। क्रेन, जो स्टील बीम को सही क्रम में ढेर कर देती है, बीम के स्थान के संदर्भ में क्रम बनाता है, लेकिन इसके संचालन के दौरान इतनी गर्मी जारी की जाएगी कि कुल एन्ट्रापी अभी भी बढ़ती है।

लेकिन फिर भी, 19 वीं शताब्दी के भौतिकविदों के ऊष्मप्रवैगिकी पर दृश्य और क्वांटम उलझाव से जुड़े दृश्य में इतना अंतर नहीं है जितना लगता है। हर बार जब कोई सिस्टम किसी बाहरी एजेंट के साथ बातचीत करता है, तो उसकी क्वांटम स्थिति एजेंट की क्वांटम स्थिति के साथ भ्रमित हो जाती है। आमतौर पर यह उलझाव सिस्टम की क्वांटम स्थिति की अनिश्चितता में वृद्धि की ओर जाता है, दूसरे शब्दों में, क्वांटम राज्यों की संख्या में वृद्धि के लिए जिसमें सिस्टम हो सकता है। अन्य प्रणालियों के साथ बातचीत के परिणामस्वरूप, सिस्टम में उपलब्ध क्वांटम राज्यों की मात्रा के संदर्भ में एन्ट्रापी, आमतौर पर बढ़ती है।

सामान्य तौर पर, क्वांटम यांत्रिकी भौतिक प्रणालियों को चिह्नित करने का एक नया तरीका प्रदान करता है जिसमें कुछ पैरामीटर (जैसे, स्थान में स्थिति) अनिश्चित हो जाते हैं, जबकि अन्य (जैसे, ऊर्जा) अक्सर सटीक रूप से ज्ञात होते हैं। क्वांटम उलझने के मामले में, सिस्टम के दो मूलभूत रूप से अलग-अलग हिस्सों में एक सामान्य कॉमन क्वांटम स्थिति होती है, और प्रत्येक भाग अलग-अलग अनिश्चित स्थिति है। उलझाव का एक मानक उदाहरण एक एकल अवस्था में स्पिन की एक जोड़ी है जिसमें यह कहना असंभव है कि किस स्पिन को निर्देशित किया गया है और जो नीचे है। , , , , .

, , , , . — , , , 2π. , , , ‑. , , , . : - ? , , , . , , 6 . , ( , ) . , 1,5 , . , , , , ; , , . , , . ( « , …», , , , .) , , : , , , , , , . , , , , , , , , . : ! , , , , , . , , , , , , . , -. , , - , .

, - , - . , , - : , . , , , , -, . , - , (, , , ). -, , , , , . - , . , 60 . , , ( ) ,



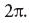
. 7.1। , a . , , t = 0. , t = 0 . , ‑.

, , « ». ? ? , . , , , . — , — , , . -, , ‑. - , , . , !

, , , — , , . «» , «», , , . 2, , , , . , , . , , ? , . , ? , , , . , , .