
परिचय
हैबर पर बहुत सारे प्रकाशन हैं जिनमें एन्ट्रापी की अवधारणा पर विचार किया जाता है, यहाँ उनमें से कुछ ही हैं [1 [5]। प्रकाशनों को सकारात्मक रूप से पाठकों द्वारा प्राप्त किया गया और बहुत रुचि पैदा हुई। यह प्रकाशन के लेखक द्वारा दी गई एन्ट्रापी की परिभाषा देने के लिए पर्याप्त है [1]: "एन्ट्रॉपी यह है कि आपको सिस्टम के बारे में कितनी जानकारी नहीं है।" हैबर पर अराजकता की घटना के बारे में प्रकाशन भी पर्याप्त हैं [6-9]। हालांकि, प्रकाशनों के दोनों समूहों में एन्ट्रॉपी और अराजकता के संबंध पर विचार नहीं किया गया था।
यह इस तथ्य के कारण है कि ज्ञान के विभिन्न क्षेत्र अराजकता के विभिन्न प्रकारों को अलग करते हैं:
- जानकारी;
- thermodynamic;
- अंतर;
- सांस्कृतिक।
अराजकता उपायों को भी उनकी विशिष्टता को ध्यान में रखते हुए वर्णित किया गया है, यहां तक कि इनमें से एक क्षेत्र में काफी मुश्किल है।
यथासंभव कार्य को सरल बनाने की कोशिश करते हुए, मैंने बिंदु मैपिंग के रूप में आरेखों पर अव्यवस्था और इन क्षेत्रों के लिए एन्ट्रापी गुणांक के रेखांकन पर अव्यवस्था के क्रम की समानता का उदाहरण का उपयोग करते हुए सूचनात्मक एन्ट्रॉपी और अराजकता के बीच संबंधों पर विचार करने का निर्णय लिया।
इसके बारे में क्या आप बिल्ली के नीचे देखकर सीखेंगे।
आदेश से अराजकता में संक्रमण के तंत्र
वास्तविक प्रणालियों और विभिन्न मॉडलों में अराजकता के क्रम से संक्रमण के तंत्र के विश्लेषण से अराजकता के संक्रमण के अपेक्षाकृत कुछ परिदृश्यों की बहुमुखी प्रतिभा का पता चला है। अराजकता के लिए संक्रमण एक द्विभाजक आरेख के रूप में दर्शाया जा सकता है (शब्द "द्विभाजन" का उपयोग प्रणाली के गुणात्मक पुनर्व्यवस्था को उसके व्यवहार के एक नए मोड के उद्भव के साथ निरूपित करने के लिए किया जाता है)।
अप्रत्याशित मोड में सिस्टम के प्रवेश को एक के बाद एक द्विभाजनों के कैस्केड द्वारा वर्णित किया जाता है। द्विभाजनों के झरना क्रमिक रूप से दो समाधानों के बीच एक विकल्प की ओर जाता है, फिर चार और इसी तरह, सिस्टम क्रमिक रूप से संभावित मूल्यों की संख्या को दोगुना करने के लिए एक अराजक, अशांत मोड में दोलन करना शुरू कर देता है।
हम पीरियड के द्विभाजन और पॉइंट मैपिंग में अराजकता की उपस्थिति पर विचार करते हैं। प्रदर्शन एक फ़ंक्शन है जो पिछले मानों पर सिस्टम पैरामीटर के निम्न मानों की निर्भरता दिखाता है:
xn+1=f(xn)= lambdaxn(1−xn)दूसरे उपयोग किए जाने वाले फ़ंक्शन पर भी विचार करें:
xn+1=f(xn)= lambda cdotxn cdot(1−x2n)बिंदु मैपिंग का उपयोग करते हुए, वस्तुओं का अध्ययन
निरंतर के साथ नहीं
, बल्कि असतत समय के साथ किया जाता है । प्रदर्शन में संक्रमण होने पर, अध्ययन के तहत प्रणाली का आयाम घट सकता है।
बाहरी पैरामीटर \ lambda को बदलते समय, बिंदु मैपिंग जटिल व्यवहार को प्रदर्शित करते हैं, जो पर्याप्त रूप से बड़े \ lambda के साथ अराजक हो जाता है। अराजकता चरण अंतरिक्ष में प्रक्षेपवक्र की एक बहुत तेजी से मंदी है।
द्विभाजन गति चित्र का एक गुणात्मक पुनर्गठन है। नियंत्रण पैरामीटर के मान जिन पर द्विभाजन होते हैं, उन्हें महत्वपूर्ण या द्विभाजन मूल्य कहा जाता है।
आरेख बनाने के लिए, हम निम्नलिखित दो सूचियों का उपयोग करेंगे:
नंबर 1। समारोह के लिए:
xn+1=f(xn)= lambdaxn(1−xn)नंबर 2. समारोह के लिए
xn+1=f(xn)= lambda cdotxn cdot(1−x2n)आलोचनात्मक मूल्यों पर उपस्कर समारोह की प्रकृति के प्रभाव का आकलन करने के लिए
lambda एक समारोह के साथ आरेख पर विचार करें
xn+1=f(xn)= lambdaxn(1−xn) ऐसा करने के लिए, हम लिस्टिंग नंबर 1 का उपयोग करेंगे:
के लिए 0 <\ lambda <1 के लिए
lambda=$0.9 और x0 = 0.47 हमें आरेख मिलता है:
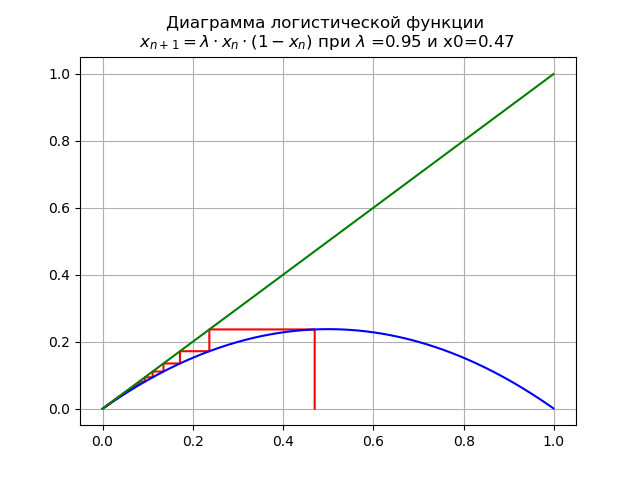
इस मामले में, नक्शे में एक निश्चित बिंदु है
x∗=0जो टिकाऊ है।
पर
1< lambda<3 के लिए
lambda=$2. x0 = 0.7 हमें आरेख प्राप्त होता है:
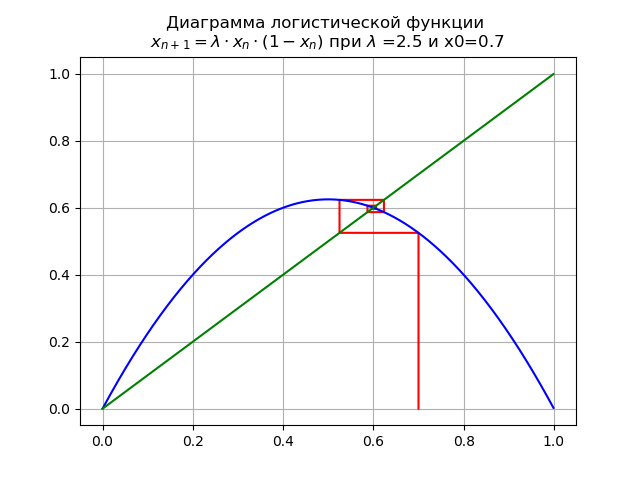
खंड [0, 1] पर, एक अन्य निश्चित बिंदु दिखाई देता है
x∗1=1−1/ lambdaपर
1< lambda<3 के लिए
lambda=$2. और x0 = 0.01 हमें आरेख प्राप्त होता है:
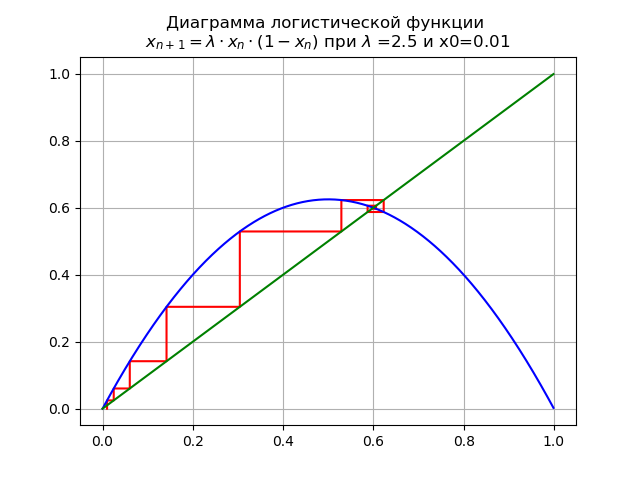
निश्चित बिंदु
x∗=0 स्थिरता खो देता है।
पर
3< lambda<3.45 के लिए
lambda=$3.4 और x0 = 0.7 हम आरेख प्राप्त करते हैं:
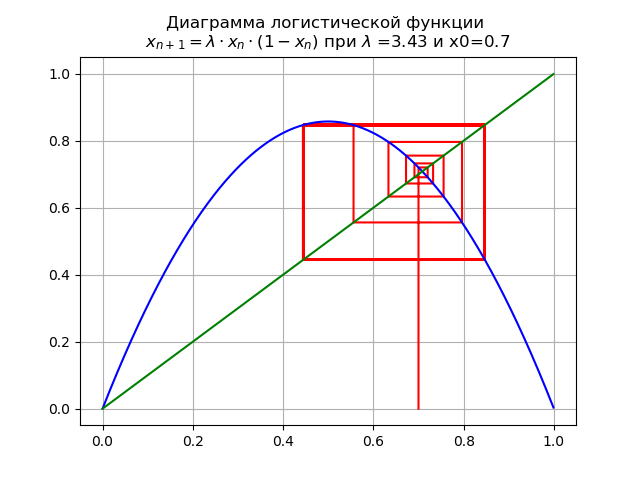
मैपिंग एक द्विभाजन से गुजरती है: निश्चित बिंदु
x∗1 अस्थिर हो जाता है, और इसके बजाय एक दोहरा चक्र दिखाई देता है।
पर
3.45< lambda<4.0 के लिए
lambda=$3.5और x0 = 0.2 हम आरेख प्राप्त करते हैं:
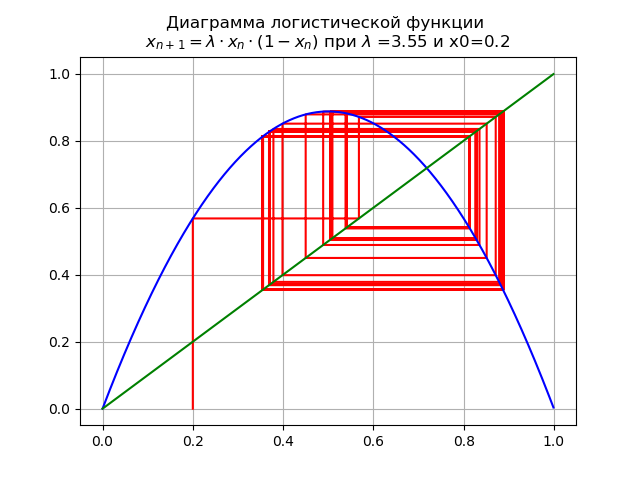
जब एक पैरामीटर पास कर रहा हो
lambda मूल्य के माध्यम से
lambda=3.45 , एक 2 गुना चक्र 4 गुना, और परे हो जाता है।
अंतिम मूल्य पर
lambda=4 प्रणाली में सभी संभावित आदेशों के अस्थिर चक्र हैं:
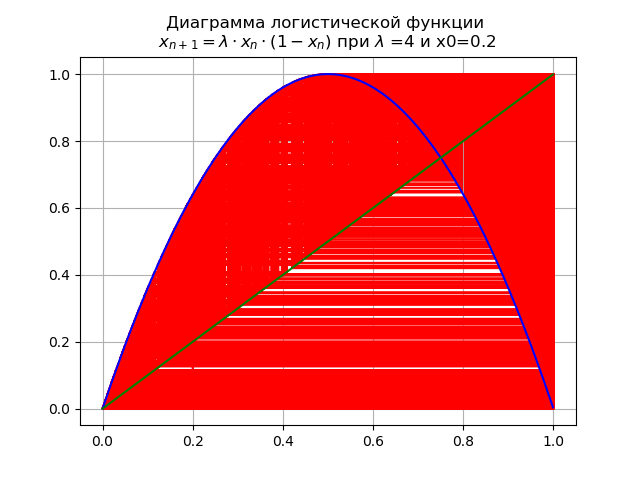
आलोचनात्मक मूल्यों पर उपस्कर समारोह की प्रकृति के प्रभाव का आकलन करने के लिए
lambda एक समारोह के साथ आरेख पर विचार करें
xn+1=f(xn)= lambda cdotxn cdot(1−x2n) , इसके लिए हम लिस्टिंग नंबर 2 का उपयोग करेंगे।
पर
0< lambda<=1.0 के लिए
lambda=0.5 और x0 = 0.2:

मानचित्रण का एक निश्चित बिंदु होता है
x∗=0 जो टिकाऊ है।
पर
1< lambda<=1.998... के लिए
lambda=$1. और x0 = 0.55:
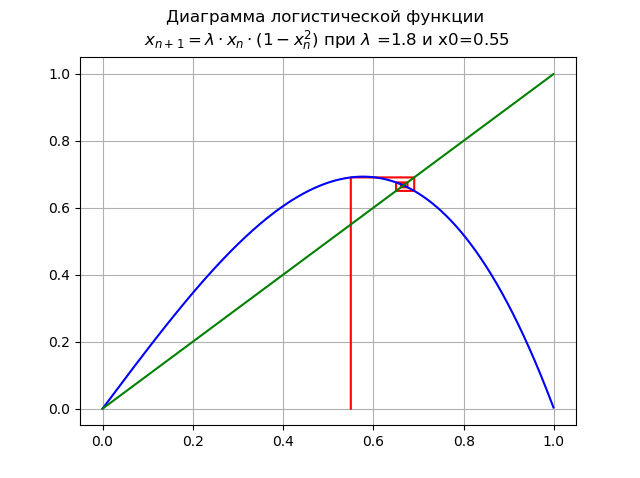
बिंदु
x∗=0 स्थिरता खो देता है, एक नया स्थिर बिंदु दिखाई देता है
x∗1पर
1.99< lambda<=2.235... के लिए
lambda=$2. और x0 = 0.2:
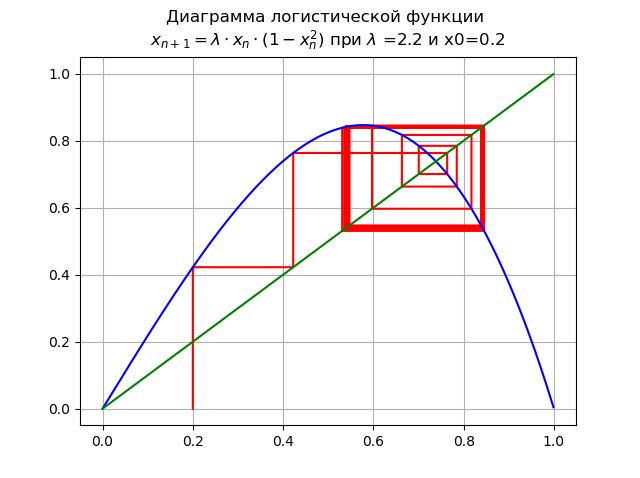
अवधि के दोहरीकरण का द्विभाजन होता है, एक 2-गुना चक्र प्रकट होता है। और बढ़ा
lambda द्विभाजक दोहरीकरण अवधि की एक झरना की ओर जाता है।
पर
2,235</lambda2.5980... के लिए
lambda=2.287 और x0 = 0.2:
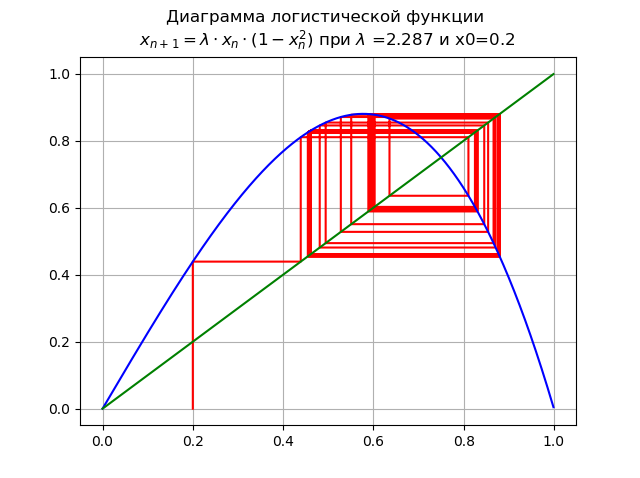
वृद्धि
lambda द्विभाजक काल दोगुनी अवधि के झरना के लिए नेतृत्व किया।
पर
lambda=2.59 प्रणाली में सभी संभावित अवधियों के अस्थिर चक्र हैं:
 जैसा कि आरेख में दिखाया गया था, लॉजिस्टिक फ़ंक्शन के क्रम में वृद्धि के साथ, परिवर्तन की सीमा lambda टेपर बंद।
जैसा कि आरेख में दिखाया गया था, लॉजिस्टिक फ़ंक्शन के क्रम में वृद्धि के साथ, परिवर्तन की सीमा lambda टेपर बंद।आरेखों का उपयोग करते हुए, हमने मूल्यों को निर्धारित करते हुए, क्रम से अराजकता तक के मार्ग का पता लगाया
lambda विभिन्न लॉजिस्टिक कार्यों के लिए। यह सवाल का जवाब देने के लिए बना हुआ है: अराजकता को कैसे मापें? लेख की शुरुआत में सूचीबद्ध कुछ प्रकार की अराजकता के लिए उत्तर ज्ञात है
- एन्ट्रापी अराजकता का एक उपाय है। इस जवाब को पूरी तरह से सूचना अराजकता के लिए जिम्मेदार ठहराया जा सकता है, हालांकि, यहां कौन सी एन्ट्रापी लागू की जाती है और संख्यात्मक मान के साथ तुलना कैसे की जाती है
lambda - मैं लेख के अगले भाग में इस सवाल का जवाब देने की कोशिश करूंगा।
सूचना एन्ट्रापी और एन्ट्रापी गुणांक
हम स्वतंत्र यादृच्छिक घटनाओं के लिए सूचना बाइनरी एन्ट्रॉपी पर विचार करेंगे।
x ग
एन संभावित राज्यों को संभाव्यता के साथ वितरित किया गया
pi(i=1,..,n) । सूचना द्विआधारी एन्ट्रापी की गणना सूत्र द्वारा की जाती है:
H(x)=− sumni=1pi cdotlog2(pi)इस मान को संदेश का औसत एन्ट्रॉपी भी कहा जाता है। मूल्य
Hi=−log2(pi) जिसे निजी एन्ट्रापी कहा जाता है, केवल
i -th अवस्था को दर्शाता है। सामान्य मामले में, एन्ट्रॉपी की परिभाषा में लघुगणक का आधार 1 से अधिक हो सकता है; उनकी पसंद एन्ट्रापी के मापन की इकाई को निर्धारित करती है।
हम दशमलव लॉगरिथम का उपयोग करेंगे जिसमें एन्ट्रापी और सूचना को बिट्स में मापा जाता है। बिट्स में जानकारी की मात्रा की गणना सही ढंग से की जाएगी, उदाहरण के लिए, चर
X और
Delta जिसमें कोई फर्क नहीं पड़ता है, लेकिन हमेशा एक ही इकाइयों में के लिए इसी अभिव्यक्तियों में प्रतिस्थापित किया जाएगा। वास्तव में:
q=H(x)−H( Delta)=log10 left(X2−X1 right)−log10(2 Delta)=log10(\)fracX2−X12 Delta)जहाँ X और
Delta एक ही इकाइयों में होना चाहिए।
प्रयोगात्मक डेटा से एक यादृच्छिक चर के एन्ट्रापी मूल्य का अनुमान निम्नलिखित संबंध से हिस्टोग्राम से पाया जाता है:
\ Delta_ {e} = \ frac {1} {2} e ^ {H (x)} = \ frac {d} {2} \ prod_ {i = 1} ^ {m} (\ frac {n}) n_ {i}}) ^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10} (n_ {i})\ Delta_ {e} = \ frac {1} {2} e ^ {H (x)} = \ frac {d} {2} \ prod_ {i = 1} ^ {m} (\ frac {n}) n_ {i}}) ^ {\ frac {n_ {i}} {n}} = \ frac {dn} {2} 10 ^ {- \ frac {1} {n}} \ sum_ {i = 1} ^ {m} n_ {i} log_ {10} (n_ {i})जहां:
ड हिस्टोग्राम के प्रत्येक स्तंभ की चौड़ाई;
एम - कॉलम की संख्या;
एन डेटा की -tal राशि;
ni - में डेटा की मात्रा
मैं वह कॉलम।
एन्ट्रापी गुणांक अनुपात से निर्धारित होता है:
ke= frac Deltae sigmaजहां:
सिग्मा - मानक विचलन।
अराजकता के उपाय के रूप में सूचना एन्ट्रापी
एन्ट्रापी गुणांक का उपयोग करके सूचना अराजकता की घटनाओं का विश्लेषण करने के लिए, हम पहले फ़ंक्शन के लिए एक शाखा आरेख बनाते हैं
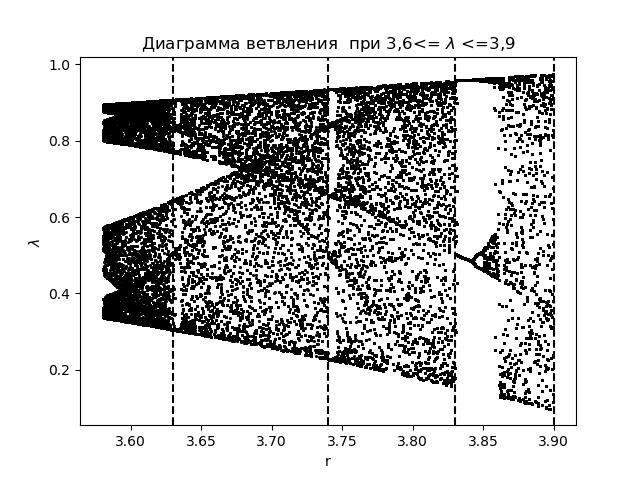
xn+1=f(xn)= lambdaxn(1−xn) हिस्टोग्राम के निर्माण के दौरान प्राप्त संक्रमण क्षेत्रों के आवेदन के साथ:
शाखा आरेख import matplotlib.pyplot as plt import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(3.58,3.9,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-y[n-1]),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title(" 3,6<= $\lambda$ <=3,9") plt.xlabel("r") plt.ylabel("$\lambda$ ") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.show()
हमें मिलता है:
हम समान क्षेत्रों के लिए एन्ट्रापी गुणांक की साजिश करते हैं
lambda :
एन्ट्रापी गुणांक के लिए ग्राफ import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(3.58,3.9,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-M[i-1,j]) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.title(" ke 3,6<= $\lambda$ <=3,9") plt.plot(arange(3.58,3.9,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=3.63,color='black',linestyle='--') plt.axvline(x=3.74,color='black',linestyle='--') plt.axvline(x=3.83,color='black',linestyle='--') plt.axvline(x=3.9,color='black',linestyle='--') plt.grid() plt.show()
हमें मिलता है:

आरेख और ग्राफ़ की तुलना करने पर, हम फ़ंक्शन के लिए एन्ट्रापी गुणांक के लिए आरेख और ग्राफ़ पर क्षेत्रों का एक समान प्रदर्शन देखते हैं
xn+1=f(xn)= lambdaxn(1−xn) ।
एन्ट्रापी गुणांक का उपयोग करके सूचना अराजकता की घटनाओं के आगे के विश्लेषण के लिए, हम लॉजिस्टिक फ़ंक्शन के लिए एक शाखा आरेख बनाते हैं:
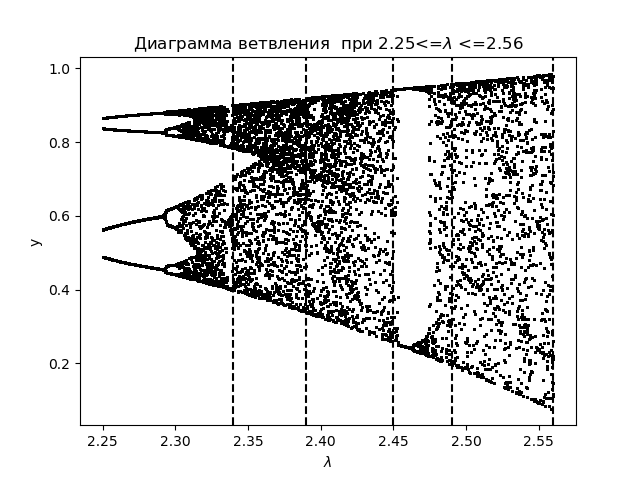
xn+1=f(xn)= lambda cdotxn cdot(1−x2n) संक्रमण क्षेत्रों के आवेदन के साथ:
शाखा आरेख import matplotlib.pyplot as plt from numpy import* N=1000 y=[] y.append(0.5) for r in arange(2.25,2.56,0.0001): for n in arange(1,N,1): y.append(round(r*y[n-1]*(1-(y[n-1])**2),4)) y=y[N-250:N] x=[r ]*250 plt.plot( x,y, color='black', linestyle=' ', marker='.', markersize=1) plt.figure(1) plt.title(" 2.25<=$\lambda$ <=2.56") plt.xlabel("$\lambda$ ") plt.ylabel("y") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.show()
हमें मिलता है:
हम समान क्षेत्रों के लिए एन्ट्रापी गुणांक की साजिश करते हैं
lambda :
एन्ट्रापी गुणांक ग्राफ import matplotlib.pyplot as plt from numpy import* data_k=[] m='auto' for p in arange(2.25,2.56,0.0001): q=[round(p,2)] M=zeros([1001,1]) for j in arange(0,1,1): M[0,j]=0.5 for j in arange(0,1,1): for i in arange(1,1001,1): M[i,j]=q[j]*M[i-1,j]*(1-(M[i-1,j])**2) a=[] for i in arange(0,1001,1): a.append(M[i,0]) n=len(a) z=histogram(a, bins=m) if type(m) is str: m=len(z[0]) y=z[0] d=z[1][1]-z[1][0] h=0.5*d*n*10**(-sum([w*log10(w) for w in y if w!=0])/n) ke=round(h/std(a),3) data_k.append(ke) plt.figure(2) plt.title(" ke 2.25<= $\lambda$ <=2.56") plt.plot(arange(2.25,2.56,0.0001),data_k) plt.xlabel("$\lambda$ ") plt.ylabel("ke") plt.axvline(x=2.34,color='black',linestyle='--') plt.axvline(x=2.39,color='black',linestyle='--') plt.axvline(x=2.45,color='black',linestyle='--') plt.axvline(x=2.49,color='black',linestyle='--') plt.axvline(x=2.56,color='black',linestyle='--') plt.grid() plt.show()
हमें मिलता है:
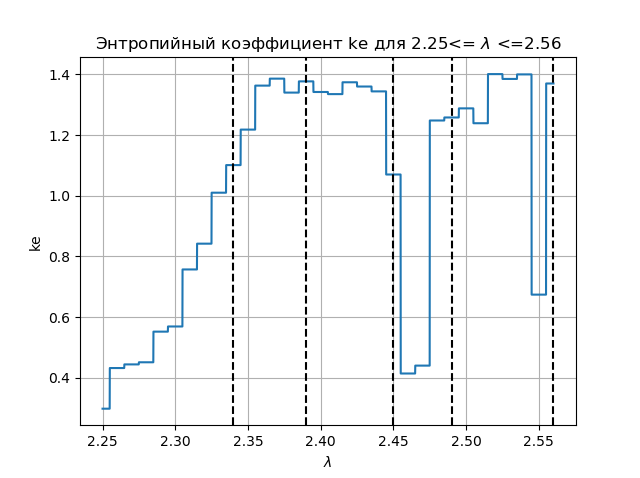
आरेख और ग्राफ की तुलना में, हम फंक्शन के लिए एन्ट्रापी गुणांक के लिए आरेख और ग्राफ पर क्षेत्रों का एक समान प्रदर्शन देखते हैं
xn+1=f(xn)= lambda cdotxn cdot(1−x2n)निष्कर्ष:
शैक्षिक समस्या को लेख में हल किया गया है: सूचनात्मक प्रवेश अराजकता का एक उपाय है, और इस सवाल का जवाब सकारात्मक रूप से पायथन द्वारा दिया गया है।
संदर्भ
- Entropy? यह आसान है!
- एन्ट्रापी और इसके कई चेहरों की अवधारणा का परिचय।
- एंट्रोपी और निर्णय पेड़।
- एन्ट्रोपी पर एक ग्रंथ।
- एन्ट्रॉपी और विनर।
- अराजकता के गणितीय मॉडल।
- अराजकता के बारे में थोड़ा और इसे कैसे बनाएं।
- लोरेंज आकर्षित करने वाले पर एक महत्वपूर्ण नज़र।
- FPGA अराजकता जनरेटर।