वैज्ञानिक समुदाय में, डेटा विज़ुअलाइज़ेशन और सिद्धांत डिजाइन बहुत महत्वपूर्ण भूमिका निभाते हैं। उपकरण जो लैटेक्स कमांड्स को लागू करते हैं, जैसे कि मार्कडाउन और मैथजैक्स, अक्सर फॉर्मूलों की सुविधाजनक और सुंदर प्रस्तुति के लिए उपयोग किए जाते हैं।

जूलिया के लिए, पैकेज का एक सेट भी है जो आपको LaTeX के सिंटैक्स का उपयोग करने की अनुमति देता है, और प्रतीकात्मक बीजगणित के साधनों के साथ मिलकर हमें सूत्रों को संभालने के लिए एक शक्तिशाली उपकरण मिलता है।

डाउनलोड करें और आज के लिए आपकी ज़रूरत की हर चीज़ को कनेक्ट करें

using Pkg Pkg.add("Latexify") Pkg.add("LaTeXStrings") Pkg.add("SymEngine") using Latexify, LaTeXStrings, Plots, SymEngine

LaTeXStrings

LaTeXStrings एक छोटा पैकेज है जो जूलिया स्ट्रिंग शाब्दिक में LaTeX समीकरण दर्ज करना आसान बनाता है। जूलिया में नियमित स्ट्रिंग्स का उपयोग करते हुए एम्बेडेड लैटेक्स समीकरणों के साथ एक स्ट्रिंग शाब्दिक दर्ज करने के लिए, आपको मैन्युअल रूप से सभी बैकस्लैश और डॉलर के संकेतों से बचना चाहिए: उदाहरण के लिए, $ \alpha^2 $ लिखा है \$\\alpha^2\$ । इसके अलावा, हालांकि IJulia LaTeX स्वरूपित समीकरणों ( MathJax के माध्यम से) को प्रदर्शित करने में सक्षम है, यह नियमित लाइनों के साथ काम नहीं करेगा। इसलिए, LaTeXStrings पैकेज परिभाषित करता है:

LaTeXString वर्ग ( String का एक उपप्रकार) जो एक स्ट्रिंग (अनुक्रमण, रूपांतरण, आदि के लिए) की तरह काम करता है, लेकिन स्वचालित रूप से IJulia में पाठ / लेटेक्स के रूप में प्रदर्शित होता है।
स्ट्रिंग मैक्रोज़ L"..." और L"""...""" जो आपको बैकस्लैश और डॉलर के संकेतों (और यदि आप उन्हें छोड़ देते हैं तो आपके लिए डॉलर के संकेत जोड़ते हैं) से भागने के बिना लाटेक्स समीकरणों को दर्ज करने की अनुमति देते हैं।

 S = L"1 + \alpha^2"

REPL आउटपुट देगा:

 "\$1 + \\alpha^2\$"

और जुपिटर प्रदर्शित करेगा :

अ ल ् फ ा

$1 + \ अल्फा ^ 2$

अनुक्रमण सामान्य रेखाओं की तरह काम करता है:

 S[4:7] "+ \\a"

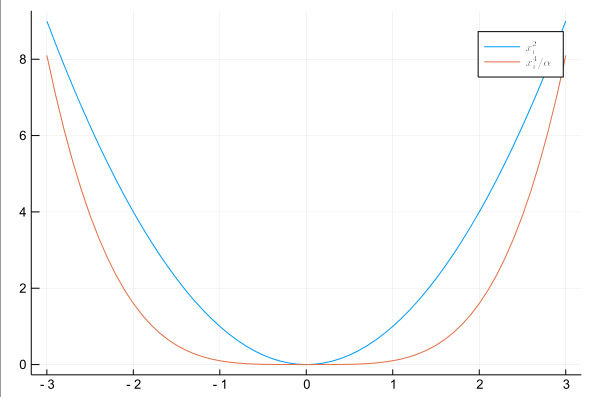
इस तरह की लाइनें रेखांकन के डिजाइन में उपयोगी हो सकती हैं।

 x = [-3:0.1:3...] y1 = x .^2 α = 10 y2 = x .^4 / α; plot(x,y1, lab = "\$x^2_i\$") plot!(x,y2, lab = L"x^4_i/\alpha")

Latexify

एक अधिक कार्यात्मक पैकेज लेटेक्सिफ़ ( गाइड ) है। इसे जूलिया ऑब्जेक्ट्स से लाटेक्स गणित उत्पन्न करने के लिए डिज़ाइन किया गया है। यह पैकेज LaTeX प्रारूप में भावों को स्ट्रिंग में बदलने के लिए जूलिया की होमोलॉजी का उपयोग करता है। लेटेक्सिफाई.ज्ल विभिन्न जूलिया वस्तुओं को परिवर्तित करने के लिए कार्य प्रदान करता है, जिसमें शामिल हैं:

भाव
लाइन,
संख्या (तर्कसंगत और जटिल सहित),
प्रतीकात्मक भाव SymEngine.jl से,
ParameterizedFunctions और ReactionNetworks डिफ़रेंशियल ईक्शंस। Jl से
साथ ही सभी समर्थित प्रकारों के सरणियाँ।

 ex = :(x/(y+x)^2) #  latexify(ex)

$\ frac {x} {\ left (y + x \ right) ^ {2}}$

 str = "x/(2*k_1+x^2)" #  latexify(str)

$\ frac {x} {2 \ cdot k_ {1} + x ^ {2}}$

विषम तत्वों की सरणी:

 m = [2//3 "e^(-c*t)" 1+3im; :(x/(x+k_1)) "gamma(n)" :(log10(x))] latexify(m)

\ left [\ start {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} और \ Gamma \ left (n \ दाएँ) और \ log_ {10} \ बाएँ (x \ दाएँ) \\ \ end {सरणी} \ right]

$\ left [\ start {array} {ccc} \ frac {2} {3} & e ^ {- c \ cdot t} & 1 + 3 \ textit {i} \\ \ frac {x} {x + k_ {1}} और \ Gamma \ left (n \ दाएँ) और \ log_ {10} \ बाएँ (x \ दाएँ) \\ \ end {सरणी} \ right]$

आप एक ऐसा फ़ंक्शन निर्दिष्ट कर सकते हैं जो फ़ार्मुलों को प्रदर्शित करता है और उन्हें उस रूप में बफर में कॉपी करता है जो कि हबर के लिए समझ में आता है:

 function habr(formula) l = latexify(formula) res = "\$\$display\$$l\$display\$\$\n" clipboard(res) return l end habr(ex)

$\ frac {x} {\ left (y + x \ right) ^ {2}}$

 <p>$<!-- math>$$display$$\frac{x}{\left( y + x \right)^{2}}$$display$$</math -->$</p>

ध्यान रखें

 latexify("x/y") |> display

$\ frac {x} {y}$

 latexify("x/y") |> print

$\frac{x}{y}$

SymEngine

SymEngine एक पैकेज है जो प्रतीकात्मक गणना प्रदान करता है जिसे आप अपने बृहस्पति में लेटेक्सिफ़ के साथ कल्पना कर सकते हैं।
आप लाइनों और उद्धरण ( quote ) में वर्ण निर्दिष्ट कर सकते हैं:

 julia> a=symbols(:a); b=symbols(:b) b julia> a,b = symbols("ab") (a, b) julia> @vars ab (a, b)

मैट्रिक्स को परिभाषित करें और खूबसूरती से इसे प्रदर्शित करें

 u = [symbols("u_$i$j") for i in 1:3, j in 1:3] 3×3 Array{Basic,2}: u_11 u_12 u_13 u_21 u_22 u_23 u_31 u_32 u_33 u |> habr

\ छोड़ दिया [\ start {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} और u_ {32} & u_ {33} \\ \ end {सरणी} \ right]

$\ छोड़ दिया [\ start {array} {ccc} u_ {11} & u_ {12} & u_ {13} \\ u_ {21} & u_ {22} & u_ {23} \\ u_ {31} और u_ {32} & u_ {33} \\ \ end {सरणी} \ right]$

मान लीजिए हमारे पास वैक्टर हैं

 C = symbols("Ω_b/Ω_l") J = [symbols("J_$i") for i in ['x','y','z'] ] h = [0, 0, symbols("h_z")] 3-element Array{Basic,1}: 0 0 h_z

जो वेक्टर-गुणा होना चाहिए

 using LinearAlgebra × = cross latexify(J×h, transpose = true)

$ $ प्रदर्शन $ $ \ _ शुरू {समीकरण} \ छोड़ [\ शुरू {सरणी} {c} J_ {y} \ cdot h_ {z} \\ - J_ {x} \ cdot h_ {z} \\ 0 \\ \ _ अंत {array} \ right] \ end {समीकरण} $ $ डिस्प्ले $$

पूर्ण मैट्रिक्स गणना:

 dJ = C*(u*J.^3)×h latexify( dJ, transpose = true) habr(ans)

$ $ प्रदर्शन $ $ \ _ शुरू {समीकरण} \ छोड़ [\ शुरू {सरणी} {c} \ frac {h_ {z} \ cdot \ left (u_ {21} \ cdot J_ {x} ^ {3} + u_ { 22} \ cdot J_ {y} ^ {3} + u_ {23} \ cdot J_ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ \ frac { - h_ {z} \ cdot \ left (u_ {11} \ cdot J_ {x} ^ {3} + u_ {12} \ cdot J_ {y} ^ {3} + u_ {13} \ cdot \ _ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}} \\ 0 \\ \ end {सरणी} \ right] \ end {समीकरण} $ $ $ $ प्रदर्शन

लेकिन इस तरह की एक सरल श्रृंखला से आप निर्धारक को खोज सकते हैं और इसे हैबर को भेज सकते हैं

 u |> det |> habr

u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ बाएँ (u_ {33}} \ _ frac) {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ _ बाईं (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)

$u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ बाएँ (u_ {33}} \ _ frac) {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ _ बाईं (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)$

Rekursivnenko! व्युत्क्रम मैट्रिक्स की गणना संभवतः इसी तरह से की जाती है:

 u^-1 |> habr

स्पॉइलर

$ $ $ $ $ \ बायाँ [\ "{सरणी} {ccc} \ frac {1 - \ frac {u_ {12} \ cdot \ left (\ frac {- u_ {21}}} {u_ {11}}} \ _ प्रदर्शित करें frac {\ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ _ \ _ u_ {31) }} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} सही) } \ right) \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {u_ {33} - \ frac [u_ {13] } \ cdot u_ {31}} {u_ {11}} - \ frac {\ _ बाईं (u_ {23} - \ frac {u_ {13} \ _ cdot u_ {21}} {u_ {11}} सही) \ _ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} / cdot u_ { 21}} {u_ {11}}}} सही)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} - \ frac {u_ [13]} \ cdot \ left (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ _ \ _ u_ {31) }} {u_ {11}} \ right)} {u_ {11} \ cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} सही) } \ right)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ _ बाएं (23_) - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u _ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}}} {u_ {11}} & \ frac {\ frac {- u_ {12} \ cdot \ left (1 + \ _ frac {\ _ बाईं ओर (u_ {23} - \ frac {u_ {13} \ _ cades u-{21}) {u_ {11}} \ राइट) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ राइट)} {\ _ बाएं (u) {22 } - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ [31}} {{ u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ / 32) - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} } (दायाँ)} \ सही)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} + \ frac {u_ {13} \ cdot का बायाँ (u_) {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {\ _ बाएं (u_ {22} - \ frac {u_ {12} \ _ cades u_ {21} } {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ _ बाएं (23) } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ [31}} {{ u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ rig ht)}} {u_ {11}} & \ frac {\ _ frac {- u_ {13}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ [11}} - \ frac {\ _ बाईं (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32) - \ frac [u_ {12] } \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} + frac { u_ {12} \ cdot \ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ _ बाएं (u_ {22} - frac { u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}) {u_ {11}} - \ _ फ़्राक {\ _ बाएं (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32) - \ f \ _ \ _ { 12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} {दाईं ओर}} } {u_ {11}} \\ \ frac {\ _ frac {- u_ {21}} {u_ {11}} - \ frac {\ _ बाईं (\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {11} / cdot \ left (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ सही)} \ दाएँ) \ cdot \ बाएँ (u_ {23} - \ frac {u_ {13}) \ cdot u_ {21}} {u_ {11}} \ right)} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ _ फ़्राक {\ _ बाएं (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32) - \ f \ _ \ _ { 12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {1 + \ _ frac {\ _ बाईं ओर (u_ {23} - \ frac {u_ / 13}} cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} {दाईं ओर}} {} \ बाएं (u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_] 13 # \ _ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ _ \ _ \ _ \ _ \ _ (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u {21}} {u_ {11}}} \ right)}} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} & \ frac {- \ left (u) {23 } - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right)} {\ _ बाएं (u_ {22} - \ frac {u_ {12} \ _ cdot u_ [21}}} { u_ {11}} \ right) \ cdot \ left (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ _ बाएं (23) -) \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac { u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right )} \\ \ frac {\ frac {- u_ {31}} {u_ {11}} + \ frac {u_ {21} \ cdot \ left (u_ {32} - \ frac {u_ {12] \ _ cdot u_ {३१}} {u_ {११}} \ दा)} {u_ {११} \ cdot \ left (u_ {२२} - \ frac {u_ {१२} \ _ cdot u_ {२१}}} {u_ {११}}} दाएँ)}} {u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ बाईं (u_ {23} - \ frac {u_ / 13} \ _) cdot u_ {21}} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} {दाईं ओर}} {} u_ {22} - \ frac {u_ {12} \ cdot u_ {21}} {u_ {11}}}} & \ frac {- \ left (u_ {32} - \ frac {u_ {12} \ _ cdot u_ {३१}} {u_ {११}} \ दा)} {\ वाम (u_ {२२}} - \ frac {u_ {१२} \ _ कूटना u_ {२१}} {u_ {११}} {दाएं) \ _ \ _ \ _ \ _} (u_ {33} - \ frac {u_ {13} \ cdot u_ {31}} {u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ _dades u_ {21] }} {u_ {11}} \ right) \ cdot \ left (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ [22} { - {frac {u_ {12} \ cdot u_ {21}} {u_ {11}}} \ right)} और \ बाएं (u_ {33} - \ frac {u_ {13} \ cdot u_ [31}} {{ u_ {11}} - \ frac {\ left (u_ {23} - \ frac {u_ {13} \ cdot u_ {21}} {u_ {11}} \ right) \ c डॉट \ लेफ्ट (u_ {32} - \ frac {u_ {12} \ cdot u_ {31}} {u_ {11}} \ right)} {u_ {22} - \ frac {u_ {12} \ _ \ _ udot { 21}} {u_ {11}}} \ right) ^ {- 1} \\ \ end {सरणी} \ right] $ $ प्रदर्शन $ $

यदि आप अपने ब्राउजर के मटजैक्स को चोट पहुंचाना चाहते हैं, तो माइनस दूसरी डिग्री (उलटा मैट्रिक्स का वर्ग) डालें
वैसे, SymEngine डेरिवेटिव्स पर विचार करता है:

 dJ[1] |> habr

\ frac {h_ {z} \ cdot \ left (u_ {21} \ cdot J_ {x} ^ {3} + u_ {22} \ _ cdot J_ {y} ^ {3} + u_ {23] \ cdot J_ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}}

$\ frac {h_ {z} \ cdot \ left (u_ {21} \ cdot J_ {x} ^ {3} + u_ {22} \ _ cdot J_ {y} ^ {3} + u_ {23] \ cdot J_ {z} ^ {3} \ right) \ cdot \ Omega_ {b}} {\ Omega_ {l}}$

 diff(dJ[1], J[1]) |> habr

$\ frac {3 \ _ cdot J_ {x} ^ {2} \ cdot h_ {z} \ cdot u_ {21} \ cdot \ Omega_ {b}} {\ Omega_ {l}}$

वैसे, जूलिया न केवल फॉर्मूले का उपयोग कर सकती हैं, बल्कि लाटेक्स के ए से ग्राफिक्स भी। और यदि आपने मिकटेक्स स्थापित किया और पहले से ही डाउनलोड किए गए pgfplots , तो उपयुक्त वातावरण का उपयोग करके आप जूलिया के साथ दोस्त बना सकते हैं, जो हिस्टोग्राम, त्रि-आयामी रेखांकन, आकृति के साथ त्रुटियों और राहतें बनाने का अवसर प्रदान करेगा, और फिर इसे लाटेक दस्तावेज़ में एकीकृत करेगा।

यह सब फ़ार्मुलों के साथ है, लेकिन प्रतीकात्मक गणनाओं के साथ नहीं: जूलिया में अभी भी प्रतीकात्मक बीजगणित के लिए अधिक जटिल और दिलचस्प समाधान हैं, जो हम निश्चित रूप से अगली बार कुछ समय के साथ निपटेंगे।

जूलिया लेटेक्स में

डाउनलोड करें और आज के लिए आपकी ज़रूरत की हर चीज़ को कनेक्ट करें

LaTeXStrings

Latexify

SymEngine

More articles: